Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Computación y Sistemas
versión On-line ISSN 2007-9737versión impresa ISSN 1405-5546
Comp. y Sist. vol.7 no.1 Ciudad de México jul./sep. 2003
Artículo
An Exponential Linear Model Matching for a Closed Kinematics Chain
Carlos Aguilar. I1, Moisés Bonilla2 and Oscar. Chavoya3
1 Centro de Investigación en Computación del IPN. Laboratorio de Metrología y Control. Av. J. de Dios Batiz s/n; México D.F., C.P. 07738.; México. E–mail: caguilar@cic.ipn.mx
2 CINVESTAV–IPN. Departamento Control Automático.
3 Camelback High School, Phoenix, AZ85016, U.S.A.
Abstract
In this paper we propose an implicit linear control law for a two degree freedom manipulator whose aim is to stabilize and match a linear model. We show that for any finite initial condition there exists a sufficient small control parameter, ε, such that the model matching is exponentially achieved.
Keywords: Parallel Robots, Lyapunov 2nd method, Stability, Implicit Systems, PD control law.
DESCARGAR ARTÍCULO EN FORMATO PDF
Appendix
Proof of the Theorem 2: Let us first separate the space of e in two regions using negativeness of the function Z (.), as follows

We proceed to consider two interesting cases: First Case: Let us first consider that e (t) never leaves Si, then

Second Case: Let us next consider that e (t) comes into Se for some T. Then by continuity of e we have

Integrating the last inequality for Δ t > 0, and using properties (15), (16) of V we get (recall a definition of 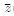 (.) (18))
(.) (18))

using now conditions (19) in the above inequality, we have that

Then e (T + Δ t) never lives Se for any arbitrary Δ t > 0. Let us finally analyze inequality (40). For this we need to consider the following to cases.

They by indication:

where  = min
= min 
References
1. C. Aguilar and M. Bonilla E. "On The Boundedness of Kinetic Energy of a Two Degree of Freedom Manipulator", ACC pp. 927–928, Philadelphia, Pennsylvania, USA, June 1998. [ Links ]
2. C. Aguilar and M. Bonilla E. "On Stabilizable Control Law For a Two a Two Degree of Freedom Manipulator", ACC pp. 2450–2454, California, USA, June 1999. [ Links ]
3. C. Aguilar and M. Bonilla E. "On Exponential Linear Model Matching for a Two Degree of Freedom Manipulator", ACC pp. 541–543, Chicago I., June 2000. [ Links ]
4. M. Bonilla and M. Malabre. "Implementing non Proper Control Law for Proper Systems" International Symposium of Implicit and Nonlinear System, SINS'92 , Ft. Worth, U.S.A. [ Links ]
5. H. Berghuis and H. Nijmeijer H., "A Passivity approach to controller–Observer design for Robots", IEEE Trans.on Robot Automat., Vol. 9, pp. 740_754, 1993. [ Links ]
6. H. Berghuis. "Observer designing in tracking control problem for Robots", proc. IFACSimp NOLCO92, Bordeaus, France, June 1992, pp.588–593. [ Links ]
7. H. Berghuis. "Robust Control of Robots using only Position measurement" Proc. IFAC World Congress, Sydney, Australia, Vol. 1, July 1993, pp. 501–506. [ Links ]
8. C. Canudas de W. and N. Fixot, " Robot Control Via Robust Estimated State Feedback" IEEE Trans, on Atom. Contr. Vol. 36, No. 12, 1991, pp. 1497–1501. [ Links ]
9. C. Canudas de W., N. Fixot, and. K.J. Astrom, "Trajectory Trackings in Robot Manipulator via Nonlinear Estimated State Feedback ", IEEE Trans, on Au–toma. Control., Vol.1, 1992, pp. 138–144. [ Links ]
10. L. Fichter (1986) "A Stewart Platform–based manipulator: General theory and practical construction" Int. J. of Robotics Research 157–182. [ Links ]
11. L. Lebret, F. Lewis (1993) "Dynamic Analysis and Control of a Stewart Platform Manipulator" J. of Robotic Systems 10(5). [ Links ]
12. F. Lewis, C.T. Abdallah and D.M. Dawson (1997) "Control Of Robot manipulators" MacMillan Publisishing Company. [ Links ]
13. J.P. Merlet (1990) "Les Robots Parallels" Hermés, Paris 1990. [ Links ]
14. Z.L. Nguyen and J. Pooran, "Learning–based control of closed–kinematic chain robot end– effort performing repetitive task, "Int. J. of Microcomputer Applications, 9, 9–15(1990). [ Links ]
15. Z.L. Nguyen, Pooran, Premack (1989) "Adaptive force/position Control of Robot Manipulators With Closed–Kinematic Chain Mechanism" in Robotics and Manufacturing: Recent Trends in Research Education, and Application. M. Jamshidi et al. Eds. ASME Press, New York, 1988. [ Links ]
16. Z.L. Nguyen, S.S. Antrazi, and C.E. Campbell, "Experimental study of motion control and trajectory planning for a Stewart platform robot manipulator," Proc. of the IEEE Int. Conf. on Robotics and Automation, Sacramento, C.A. 1991, pp. 1873–1878. [ Links ]
17. Nguyen, Pooran (1989) "Dynamic Analysis of a 6 DOF CKCM Robot End–effector for Dual–arm Telero–bot Systems" J. of Robotics and Autonomous Systems, 5, 377–394. [ Links ]
18. S. Nicosia and P. Tomei. "Robot Control by using only Joint Position Measurements", IEEE Trans, on Automat. Contr., Vol.35, No. 1990, pp.1058–1061. [ Links ]
19. J.P. Reboulet and P. Pigeyre "Hybrid control of a six–degree–of–freedom in parallel actuated micro–manipulator mounted on a Sacara Robot,"in Robotics and Manufacturing, Eds., ASME Rress, N.Y., 1990, Vol. 3, pp. 293–298. [ Links ]
20. M. D. Di Benedetto and J. W. Grizzle. "Asymptotic Model Matching for Nonlinear Systems", IEEE Trans, on Automat. Contr., Vol. 39, No. 8 pp. 1539–1550, 1994. [ Links ]
21. C. I. Byrnes, A. Isidori and R. Castro, "Linear model matching with prescribed tracking error and internal stability", in Analysis and Optimization of Systems, Bensoussan and Lions (eds.), (Lecture Notes in Control and Information Sciences) vol. 111. Berlin: Springer – Verlag, 1988, pp. 249–258. [ Links ]
22. M. D. Di Benedetto and A. Isidori, "The matching of nonlinear models via dynamic state feedback", SIAM J. Contr. Opt., Vol. 24, No. 5, pp. 1063–1075, 1986. [ Links ]
23. H. J. C. Huijberts and H. Nijmeijer, "Local nonlinear model matching: From linearity to nonlinearity", Automática, 26, pp. 173–183, 1990. [ Links ]
24. R. Dunlop and A. C. Garcia, "A nitinol wire actuated Stewart platform", Proc. 2002 Australasian Conf. on R. and A., Auckland, pp. 27–29, 2002. [ Links ]
25. R. Dunlop and T.P. Jones, "Position analysis of a 2 DOF parallel manipulator nitinol", Journal of Mechanism and Machine Theory, Vol (34) 4, pp. 599–614, 1998. [ Links ]














