Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Madera y bosques
versión On-line ISSN 2448-7597versión impresa ISSN 1405-0471
Madera bosques vol.21 no.3 Xalapa sep./dic. 2015
Artículos científicos
Modelos de crecimiento y rendimiento de totalidad del rodal para Pinus patula
Whole-stand growth and yield models for Pinus patula
Wenceslao Santiago-García1*, Héctor Manuel De los Santos-Posadas2, Gregorio Ángeles-Pérez2, José René Valdez-Lazalde2, José Javier Corral-Rivas3, Gerardo Rodríguez-Ortiz4 y Elías Santiago-García5
1 Instituto de Estudios Ambientales. Universidad de la de Juárez, Oaxaca. Ixtlán de Juárez. Oaxaca, México. * Autor para correspondencia. wsantiago@unsij.edu.mx
2 Postgrado en Ciencias Forestales. Campus Montecillo. Colegio de Postgraduados. Montecillo, Texcoco, Edo. de México, México. hmsantos@colpos.mx
3 Instituto de Silvicultura e Industria de la Madera. Universidad Juárez del Estado de Durango. Durango, México.
4 División de Estudios de Posgrado e Investigación. Instituto Tecnológico del Valle de Oaxaca. Oaxaca, México.
5 Dirección Técnica Forestal de la comunidad de Ixtlán Sierra Juárez. Ixtlán de Juárez, Oaxaca, México.
Manuscrito recibido el 5 de diciembre de 2014.
Aceptado el 15 de septiembre de 2015.
Resumen
La predicción del crecimiento y el rendimiento de una especie forestal maderable es un requisito fundamental para planificar su manejo racional. El objetivo de este trabajo fue actualizar las funciones que componen un sistema compatible de crecimiento y rendimiento para Pinus patula, desarrollado bajo el enfoque de modelos explícitos de totalidad del rodal. Se reajustaron los parámetros del sistema mediante la técnica de regresión aparentemente no relacionada. Para ello, se utilizó información dasométrica derivada de cuatro inventarios realizados periódicamente en 42 parcelas permanentes de muestreo de 400 m2 en Hidalgo, México. La estructura de las funciones originales del sistema, en su mayoría, generaron buen ajuste y comportamiento gráfico satisfactorio. La productividad del rodal se describe mediante un patrón polimórfico de crecimiento, el cual está interrelacionado con las ecuaciones de área basal, diámetro promedio y volumen total de fuste por hectárea. La función de mortalidad corresponde a un modelo exponencial ajustado bajo mínimos cuadrados no lineales. El reajuste del sistema permitió ampliar el rango de validez de las ecuaciones de crecimiento a 31 años de edad del rodal. El nuevo sistema sugiere un turno técnico que maximiza el volumen de alrededor de 20 años para el sitio promedio. Este resultado sugiere que el turno de 40 años, actualmente usado en los planes de manejo en la región, puede ser acortado, siempre y cuando la densidad del rodal se maneje correctamente.
Palabras clave: diferencia algebraica, modelos compatibles, predicción explícita, sistema de crecimiento, turno técnico.
Abstract
Predicting the growth and yield of timber tree species is a prerequisite for planning sustainable forest management. The objective was to update several functions that integrate a compatible growth and yield system for Pinus patula, developed under the explicit whole-stand model approach. System parameters were estimated using seemingly unrelated regression. For that, forest biometric information was used from four periodical inventories conducted in 42 permanent plots of 400 m2 in Hidalgo, Mexico. Almost all the functions of the system had good fit and satisfactory graphical behavior in their original structure. A polymorphic growth pattern explains stand productivity, which is interrelated with growth equations of basal area, mean diameter and total stem volume per hectare. The mortality function corresponds to an exponential model fitted under non-linear least squares method. The refitted system broadened the range of the growth equations to 31 years. The new system suggests a maximizing volume rotation of about 20 years for the average site. These results suggest that the commonly used 40 year rotation period used in the management plans in the region could be shortened if a proper density management strategy is applied.
Keywords: algebraic difference, compatible models, explicit prediction, growth system, optimum rotation age.
Introducción
La planificación adecuada del uso o aprovechamiento de un bosque hace necesario que sus administradores cuenten con herramientas silvícolas cuantitativas confiables, que les permitan pronosticar el crecimiento y el rendimiento maderable esperado. Los sistemas de crecimiento y rendimiento maderable (SCRM) constituyen una parte de estas herramientas. En bosques bajo manejo forestal maderable es necesario contar con modelos para predecir la dinámica de rodales en una amplia variedad de condiciones y opciones de manejo (García, 1994; Vanclay, 1994; Davis et al., 2001).
Un SCRM es un conjunto de modelos que describen de manera cuantitativa la dinámica del crecimiento en un rodal forestal. Esta dinámica es reflejada en los cambios de magnitud de las variables del rodal como la altura dominante, el diámetro promedio de los árboles, el área basal, el número de árboles por unidad de superficie y el volumen. Cada ecuación en el sistema describe una relación diferente entre un conjunto de variables, pero se asume que todas las relaciones ocurren simultáneamente (Borders y Bailey, 1986).
Los SCRM se pueden clasificar en compatibles y no compatibles, dependiendo del grupo de relaciones simultáneas entre sus componentes. Los SCRM no compatibles generalmente constituyen un grupo de modelos en que se ignora la interdependencia entre los componentes del crecimiento, y los parámetros de cada ecuación se estiman de forma separada (Borders y Bailey, 1986). Por otra parte, en SCRM compatibles los componentes del crecimiento están relacionados entre sí (Buckman, 1962; Clutter, 1963); además, se considera que la integral de la curva que describe la tasa de crecimiento es igual al rendimiento, cuando se evalúa en un intervalo de tiempo (Borders y Bailey, 1986; Borders, 1989). Como alternativa, existe el desarrollo de ecuaciones de diferencia algebraica (ADA, algebraic difference approach) para generar SCRM compatibles, también llamadas funciones de transición, que describen las tasas de cambio del sistema en cualquier punto del tiempo, en función de su estado actual (Ramírez et al., 1987; García, 1988; García, 1994).
Santiago-García et al. (2013) ajustaron un SCRM compatible de totalidad del rodal para bosques coetáneos de Pinus patula de la región de Zacualtipán, Hidalgo, México. Este tipo de modelos, generalmente, es el más adecuado para el manejo de rodales coetáneos y plantaciones forestales, porque representa un buen compromiso entre generalidad y precisión de las estimaciones (García, 1988; Vanclay, 1994; Diéguez-Aranda et al., 2006a). El sistema para P. patula fue generado utilizando datos de tres inventarios realizados durante los años 2005, 2006 y 2008 en sitios permanentes de investigación silvícola, siendo válido para rodales de entre 8 y 27 años de edad. Durante 2012, se realizó una cuarta remedición de los sitios permanentes, lo que permite reajustar el SCRM.
Objetivo
Actualizar las ecuaciones que integran el SCRM compatible desarrollado por Santiago-García et al. (2013), bajo el enfoque de modelado explícito a nivel de rodal, para las masas naturales coetáneas de Pinus patula en la región de Zacualtipán, Hidalgo, México.
Materiales y métodos
Área de estudio
El estudio se realizó al sureste del municipio de Zacualtipán de Ángeles, Hidalgo, México, en la provincia fisiográfica denominada Sierra Madre Oriental y Subprovincia Sierra de Zacualtipán. Los rodales estudiados se localizan entre 20° 36' 44'' y 20° 37' 49'' LN y 98° 35' 30'' y 98° 37' 46'' LO, con altitud media de 2060 m. El suelo de las partes bajas es Feozem háplico (Hh), con una capa superficial obscura, suave y rica en materia orgánica, mientras que en las partes con mayor pendiente es Regosol calcárico (Rc). El clima es C(fm) w"b(e)g, templado-húmedo con lluvias todo el año, temperatura media anual de 13.5 °C y precipitación anual de 2050 mm. En las últimas tres décadas, la masa forestal del área de estudio se ha orientado hacia el desarrollo de rodales coetáneos de P. patula (Aguirre-Salado et al., 2009).
Datos dasométricos
Los datos utilizados en el estudio se colectaron en cuatro inventarios realizados en 42 parcelas permanentes de muestreo de 400 m2, durante los años 2005, 2006, 2008 y 2012; dichas parcelas cubren diferentes intervalos de densidad, calidad de sitio y edad de rodales puros y coetáneos de P. patula (Tabla 1). Los datos colectados fueron: altura total (m) de todos los árboles (obtenida con clinómetro digital® y con una curva diámetro-altura), de los cuales, cuatro se identificaron como dominantes (Hd) de acuerdo con la definición de altura dominante que corresponde a los 100 árboles más altos por hectárea (Assman, 1970; Alder, 1980); diámetro normal (medido con cinta diamétrica®) de todos los árboles (Dn, cm) y número de árboles vivos (Na).

Las variables de estado estimadas por hectárea, a partir de estos datos fueron: altura promedio de los árboles dominantes (HD, m), diámetro promedio (DP, cm), área basal (AB, m2), volumen total (V, m3) y número de árboles vivos (NA). En el análisis estadístico se utilizó la información dasométrica de las parcelas no intervenidas, es decir, con mortalidad natural. Solo en el caso de la estimación de la altura promedio de los árboles dominantes se utilizó la totalidad de las parcelas inventariadas (intervenidas y no intervenidas).
Desarrollo de modelos compatibles
Para reajustar el modelo compatible en HD (Santiago-García et al., 2013), se utilizaron 126 pares de datos no traslapados, correspondientes al promedio de alturas dominantes y edades que van de 8 años a 31 años (Tabla 1). En general, el modelo de diferencia algebraica (ADA) que define la familia de curvas de índice de sitio (IS) tiene la forma: Y2 = f(Y1, E2, E1, β), donde: Y2 = valor de la variable analizada del rodal a una edad E2 (edad de proyección), Y1 = variable de interés medida a una edad E1 (edad inicial) y β = vector de parámetros de regresión (Clutter et al., 1983; Diéguez-Aranda et al., 2005; Magaña et al., 2008).
La actualización del patrón de crecimiento para la función f(.) presenta una hipótesis de crecimiento polimórfica basada en el modelo de Hossfeld IV (Ecuaciones 1 y 2). Con este patrón, las tasas de crecimiento son variables entre sitios forestales, pero la potencialidad máxima es constante, dando origen a curvas de asíntota común, también conocidas como curvas polimórficas (Gómez-Tejero et al., 2009).
Se debe tener en cuenta que el patrón de crecimiento en altura dominante afectará a todo el sistema en el momento en que HD o IS se utilicen como variables independientes en cualquiera de los otros modelos que conforman el SCRM. La estructura del modelo de Hossfeld IV (Kiviste et al., 2002; De los Santos-Posadas et al., 2006; Gómez-Tejero et al., 2009) es:

Al resolver la ecuación por b1, se obtiene el siguiente modelo polimórfico de proyección en diferencia algebraica:

donde HD1 y HD2 corresponden a la altura dominante en E1 y E2, ln indica el logaritmo natural, exp es la función exponencial y bi son los parámetros a estimar.
En el reajuste del resto de las variables del SCRM se utilizaron 100 pares de datos no traslapados, correspondientes a E1 y E2 (Tabla 1). El paso inicial para la construcción de los modelos compatibles de área basal, diámetro promedio y volumen total, consistió en definir las ecuaciones de predicción para caracterizar el estado promedio del rodal a una edad definida. En este caso, las ecuaciones se basaron en modificaciones del modelo básico de rendimiento de Schumacher (1939) y Clutter (1963). El segundo paso fue desarrollar una forma de diferencia de las ecuaciones de predicción. La forma de obtener un modelo compatible se ejemplifica a continuación, para el modelo de área basal. La ecuación de predicción es (Santiago-García et al., 2013):

donde: AB1 = área basal (m2 ha-1) a la edad E1, DP1 = diámetro promedio (cm) a la edad E1, IS = índice de sitio del rodal (m), NA1 = número de árboles (ha-1) a la edad E1 y α. = parámetros a estimar en el modelo.
Si se linealiza la ecuación 3 para los estados E1 y E2, se obtienen las ecuaciones siguientes:

donde: AB2 es el área basal (m2 ha-1) a la edad E2, DP2 es el diámetro promedio (cm) a la edad E2, NA2 es el número de árboles (ha-1) a la edad E2, lo demás ya se definió previamente.
Al diferenciar ambos lados y despejar ln (AB2) se obtiene:

Esta es la forma lineal del modelo de proyección para el logaritmo de AB. Si se aplica la función exponencial en ambos lados de la ecuación, se obtiene el modelo no lineal de proyección siguiente:

La presencia y combinación de variables predictoras como DPi y NAi, en la ecuación 4, requiere de modelos de crecimiento para estas variables en particular. Así, para el DPi, se tiene el siguiente par de ecuaciones compatibles de predicción y proyección:


donde: bi son los parámetros a estimar, lo demás ya fue definido con anterioridad.
Para el volumen total se reajustaron las siguientes ecuaciones compatibles:
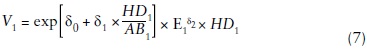

donde: V1 es el volumen (m3 ha-1) a la edad E1, V2 es el volumen (m3 ha-1) a la edad E2, δ. son los parámetros a estimar, lo demás ya fue definido.
Para pronosticar el número de árboles sobrevivientes en un tiempo determinado se ajustaron las siguientes funciones de mortalidad (Torres y Magaña, 2001; Zhao et al., 2007):


Ajuste del sistema y análisis estadístico
Cada componente del SCRM se reajustó de manera simultánea, a través de regresión aparentemente no relacionada (SUR, seemingly unrelated regression), mediante el procedimiento MODEL de SAS/ETS® (SAS Institute Inc., 2011), con excepción de las funciones de mortalidad, que se ajustaron a través de mínimos cuadrados no lineales.
Como criterios de evaluación de la bondad de ajuste de los modelos se utilizaron la suma de cuadrados del error (SCE), el cuadrado medio del error (CME), el coeficiente de determinación (R2) y, para las ecuaciones de mortalidad, el sesgo (Ē) en la proyección del NA (Corral-Rivas et al., 2004; Zhao et al., 2007). La técnica de estimación de parámetros SUR proporciona una mejora en la estimación de parámetros de regresión, porque utiliza las correlaciones entre los errores en un sistema de ecuaciones; además, permite compatibilidad total entre el modelo de predicción y el de proyección, de forma que los parámetros comunes de ambas ecuaciones toman los mismos valores mientras se cumple con el criterio de minimización de los cuadrados de los residuos (Galán et al., 2008).
Los modelos descritos son intrínsecamente no lineales, por lo que la estimación de los parámetros requiere el empleo de un proceso iterativo (Diéguez-Aranda et al., 2005); en este caso, se utilizó el algoritmo de Gauss-Newton que está implementado en el procedimiento MODEL de SAS/ETS® (SAS Institute Inc., 2011).
Resultados
Altura dominante e índice de sitio
La información dasométrica de sitios permanentes de muestreo permitió aplicar el método de desarrollo de curvas de diferencia algebraica. Los modelos generaron ajustes que explicaron 91.0 % (predicción, Ec. 1) y 96.8 % (proyección, Ec. 2) de la varianza total observada en la altura dominante, siendo todos sus parámetros significativos y con valores bajos en su error estándar (Tablas 2 y 3).

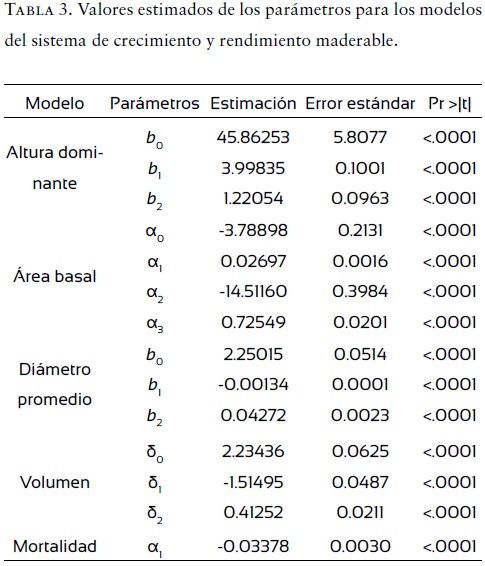
El análisis estadístico muestra que el modelo polimórfico de Hossfeld IV es adecuado, presenta un valor alto del coeficiente de determinación (R2), para ambas ecuaciones de predicción y proyección, y valores más reducidos de SCE y CME para el modelo de proyección (Ec. 2). En la figura 1 se presenta el comportamiento gráfico de los modelos de crecimiento en altura dominante.
La ecuación polimórfica b1 de Hossfeld IV, bajo la formulación ADA que expresa el índice de sitio (IS) para P. patula a una edad base (Eb) de 40 años se explica en el modelo 11.

El IS se refiere a la altura dominante del rodal a una edad de referencia, lo que permite al silvicultor clasificar y proyectar el crecimiento del rodal y, por tanto, representa un medio eficaz y simplificado para estimar la productividad forestal (Clutter et al., 1983; García et al., 1998; Torres y Magaña, 2001; De los Santos-Posadas et al., 2006). La estimación precisa del nivel de productividad es fundamental en el manejo forestal, porque contribuye a determinar la cosecha de madera y el periodo de rotación, además de ayudar a la toma de decisiones acerca de la elección de las especies más adecuadas para cierta localización (Vargas-Larreta et al., 2010). Así, se considera que la calidad de sitio expresada mediante HD o IS en conjunto con la edad son las variables predictoras más importantes en los modelos de crecimiento y rendimiento maderable.
Reajuste de las ecuaciones compatibles
La actualización de las ecuaciones de HD e IS permitió continuar con el reajuste del SCRM, ya que fueron de utilidad para explicar el crecimiento en diámetro promedio, área basal y volumen. El ajuste y los parámetros estimados para el resto de las ecuaciones que integran el SCRM muestran un alto nivel de precisión, al explicar de 84.5% a 99.7% de la variación total observada en las variables de interés (Tabla 2). La significancia de los parámetros (p < 0.0001) y los valores reducidos para los errores estándar asociados a cada uno de ellos, hacen robustos y confiables los modelos de crecimiento (Tabla 3). De estos, los modelos de proyección destacan por presentar valores más bajos de SCE y CME, así como R2 con valores más altos, respecto a los modelos de predicción.
El modelo actualizado de área basal (Modelo AB A), genera un patrón de crecimiento con características deseables en una curva de crecimiento: forma sigmoide con un punto de inflexión y tendencia a alcanzar una asíntota horizontal a edades avanzadas (Kiviste et al., 2002). Asimismo, tiene capacidad predictiva similar al modelo previo (Modelo AB P). La actualización, genera predicciones más optimistas en edades jóvenes y produce estimaciones menores en edades posteriores a los 20 años (Fig. 2). En esta etapa es preferible tener estimaciones conservadoras en área basal, y consecuentemente, en volumen maderable. Las características de los parámetros en ambos modelos reflejan su eficiencia estadística porque tienen errores estándar reducidos y son significativos. Los criterios estadísticos del modelo de AB P pueden consultarse en Santiago-García et al. (2013).

El empleo del modelo de crecimiento en diámetro promedio proporciona gran flexibilidad, porque puede utilizarse para cualquier nivel de densidad, edad y calidad de sitio. En la figura 3 se presentan las curvas de crecimiento para el diámetro promedio obtenidas mediante la ecuación previa (Modelo DP P) y actualizada (Modelo DP A). El comportamiento del modelo de crecimiento en diámetro promedio es coherente de acuerdo con los datos observados.

Modelar toda la variabilidad posible del DP es difícil porque su crecimiento está afectado por el nivel de productividad y la densidad del rodal principalmente. Intervenciones como los aclareos (por ejemplo, aclareos por lo bajo) producen un cambio instantáneo en el valor de esta variable, por ello, en la actualización del modelo de crecimiento en DP solo se utilizó la información de las parcelas sin aclareos. Como se aprecia en la figura 3, el modelo actualizado (DP A) de crecimiento en diámetro promedio, produce estimaciones más optimistas respecto al modelo previo (DP P).
El modelo previo de volumen total por hectárea (Modelo V P) y el modelo actualizado (Modelo V A) generan curvas de crecimiento similares, dado que su estructura matemática es la misma. No obstante, al igual que el modelo en área basal, este modelo actualizado genera predicciones ligeramente más optimistas en edades jóvenes y produce estimaciones más conservadoras en edades posteriores a los 20 años (Fig. 4).

Uno de los problemas principales para estimar el rendimiento futuro es el poder pronosticar el número de árboles sobrevivientes por unidad de superficie, sobre los cuales se distribuirá el volumen proyectado (Magaña et al., 2008). El comportamiento de la función de mortalidad (Ec. 9) ajustada por Santiago-García et al. (2013), se muestra razonable de acuerdo con los datos observados en campo (Fig. 5A), presenta una tasa de mortandad de 3.3 % anual y un sesgo de 2.25. El reajuste de esta ecuación (NA2 = NA1xexp[-0.04801x (E2-E1)j) generó una tasa de mortandad anual de 4.6%, la cual es más severa y con mayor sesgo en la proyección (36.6), de acuerdo con los datos observados (Fig. 5B). Asimismo, la incorporación del IS en la función de mortalidad: NA2 = NA1xexp[-0.0017xISx(E2-E1)j (Fig. 5C), genera tasas variables de mortalidad, las cuales tienden a ser mayores en las mejores calidades de sitio.
Para el sitio promedio (IS = 29 m) generó una tasa de mortandad de 4.8 % anual. Sin embargo, el sesgo en la proyección (37.1) es mayor respecto a la ecuación original. Debido a esta situación, se decidió descartar la incorporación de estas expresiones en la actualización del SCRM y mantener la ecuación de mortalidad con sus parámetros originales, por ser más consistente y generar menor sesgo en las estimaciones. Así, es recomendable el uso de la ecuación original en el conjunto del SCRM. No obstante, es necesario explorar con mayor detalle el comportamiento de la mortalidad en diferentes niveles de densidad del rodal, porque es de esperarse que los rodales más densamente poblados presenten tasas más altas de mortalidad respecto a rodales menos densos. En ese sentido, es posible determinar distintos patrones de mortalidad, lo cual hace factible la posibilidad de incluir en el SCRM más de una función de mortalidad que refleje esta dinámica.
Con esta ecuación (Ec. 9) se estima el número de árboles sobrevivientes (NA2), a partir del número actual de árboles (NA1) y la edad actual del rodal (E1), fijando un periodo de proyección (E2).
Uso del SCRM
El principal uso de las ecuaciones del SCRM es la simulación de escenarios de manejo, donde a través de una tabla de rendimiento se muestra el cambio en la magnitud de cada una de las variables dasométricas de interés a medida que cambia su edad. Sin embargo, el SCRM propuesto, representa múltiples tablas de rendimiento e innumerables combinaciones para el manejo de la densidad. En la tabla 4 se presenta una tabla de rendimiento de densidad variable, para los rodales de P. patula en los IS más comunes del estudio (27 m y 29 m de HD).
La calidad de sitio permite distinguir distintos niveles de incremento corriente anual (ICA) e incremento medio anual (IMA) en volumen, con lo que es posible definir la edad a la que ocurre el turno técnico, es decir, la edad óptima de cosecha del rodal, si se desea maximizar el volumen total (la edad cuando ICA = IMA). El comportamiento de los incrementos (Tabla 4) indica que el turno técnico ocurre alrededor de los 20 años para el IS de 29 m y a los 22 años para el IS de 27 m, bajo el mismo nivel de densidad inicial en plantas vivas al año 1. De estos resultados, se destacan dos factores que determinan la edad a la que ocurre el turno técnico: la calidad de sitio y el nivel de densidad.
Es factible que bajo una silvicultura intensiva se puedan generar planes de manejo con un turno de alrededor de 20 años en los mejores sitios, siempre y cuando se pueda cumplir con los siguientes requisitos: 1) se promueva una rápida repoblación del rodal después de la cosecha final y 2) se apliquen, en tiempo y forma, prácticas de control de la vegetación competidora y de manejo de la densidad.
Una función básica de un SCRM es que también puede proveer actualizaciones del inventario, cuando se carece de remediciones en la red de sitios permanentes diseñada para ello. Dependiendo de la calidad y el tiempo entre remediciones, el SCRM permite: 1) estimar el inventario a partir de un inventario previo, o 2) a partir de una actualización de este tipo, estimar el nuevo tamaño de muestra en caso de que se requiera un nuevo inventario operativo.
Discusión
Altura dominante e índice de sitio
Se observó que la familia de curvas polimórficas (Fig. 1B) describen mejor el patrón de crecimiento en comparación con las curvas anamórficas desarrolladas por Santiago-García et al. (2013) (Fig. 1A). La actualización del modelo de Hossfeld IV para describir el crecimiento en altura dominante de P. patula supone la incorporación de nuevos datos, lo que incrementa el rango de edad y, por tanto, permiten hacer una mejor estimación de la asíntota horizontal (b0 = 45.86 m), cuyo valor fue superior al obtenido para el modelo anamórfico (38.98 m). Esta estimación más alta de la asíntota permitió caracterizar de mejor manera la calidad de estación a través de curvas polimórficas y sugiere que la tasa relativa de crecimiento es específica del sitio, por lo que una mejor calidad de sitio, reduce el turno técnico en HD y en consecuencia, en volumen.
El modelo polimórfico desarrollado en este estudio coincide con lo obtenido por Gómez-Tejero et al. (2009), al encontrar que la familia polimórfica 1 (derivada de b1) de Hossfeld IV es la más adecuada para describir la altura dominante de plantaciones de Eucalyptus urophylla S. T. Blake en Oaxaca, México. En adición, Torres y Magaña (2001) señalan que en años recientes se ha dado mayor énfasis al desarrollo de funciones de IS polimórficas, porque se ha comprobado que tales tendencias se aproximan más a la tendencia real del crecimiento en altura. Al respecto, Corral-Rivas et al. (2004) mencionan que las funciones anamórficas generalmente no son adecuadas para representar el crecimiento en altura dominante, porque la forma de las curvas varía entre sitios, por tanto, el crecimiento en esta variable es realmente polimórfico.
Como ejemplos de ello se puede mencionar el trabajo de Amaro et al. (1998), para plantaciones de eucaliptos en Portugal, y el trabajo de Corral-Rivas et al. (2004), para bosques naturales de Pinus cooperi Blanco, P. durangensis Martínez, P. engelmannii Carr, P. leiophylla Schl. et Cham. y P. herrerae Martínez en Durango, México; así como el trabajo de Rodríguez-Acosta y Arteaga-Martínez (2005) para P. chiapensis (Martínez) Andresen en Veracruz y Puebla, México.
Asimismo, en los últimos años también se ha dado énfasis a los modelos de diferencia algebraica generalizada (GADA, generalized algebraic difference approach). Este enfoque tiene la ventaja de ampliar la base de ecuaciones de acuerdo con varias teorías sobre las características del crecimiento, lo que permite más de un parámetro específico por sitio y hace más flexibles las ecuaciones dinámicas. Lo anterior, da la posibilidad de simular polimorfismo con múltiples asíntotas (Cieszewski y Bailey, 2000; De los Santos-Posadas et al., 2006; Diéguez-Aranda et al., 2006b; Vargas-Larreta et al., 2010). El modelo de Hossfeld IV es tan flexible que, además de sus familias ADA, permite generar familias GADA, en las que tanto la asíntota, como la tasa de crecimiento, pueden variar con el sitio (Gómez-Tejero et al., 2009).
Reajuste de las ecuaciones compatibles
El nivel de precisión del SCRM actual (R2 = 0.845 - 0.997), es similar al 88.4% - 99.7% obtenido en estudio previo (Santiago-García et al., 2013). Asimismo, a lo obtenido por Galán et al. (2008), quienes con base en datos de sitios con remediciones y mediante regresión SUR, desarrollaron un sistema compatible para Cedrela odorata L. y Tabebuia donnell-smithii Rose, cuya precisión explica de 89.6 % a 99.6 % de la variabilidad total observada en la altura dominante, área basal y volumen. Similares niveles de precisión obtuvieron Magaña et al. (2008), al desarrollar un sistema de ecuaciones para predecir el crecimiento y rendimiento de Pinus rudis Endl., en Aloapan, Oaxaca, con base en datos de la misma naturaleza.
Al incluir como variable predictora alguna función de la densidad del rodal como lo es el número de árboles por hectárea (NA), se da al sistema la connotación de "densidad variable", propiedad ideal para simular regímenes silviculturales etiquetados para distintos IS. Otra cualidad que se destaca de este tipo de modelos es la invarianza con respecto al camino de proyección, es decir, los valores pronosticados para un instante futuro a partir de un estado inicial deben ser iguales, independientemente del número de pasos utilizados en su predicción (Sullivan y Clutter, 1972; Diéguez-Aranda et al., 2005). Sullivan y Clutter (1972) y García (1994) definen esta cualidad como composición o propiedad de semigrupo, esto es, el resultado de proyectar el estado, primero de E0 a E1 y luego de E1 a E2, debe ser el mismo que el de la proyección en una sola etapa de E0 a E2.
El modelo de predicción de área basal (Ec. 3) considera como variables predictoras: la edad del rodal, el número de árboles por hectárea, el índice de sitio y el diámetro promedio del rodal. Por su parte, su correspondiente modelo de proyección (Ec. 4), excluye al índice de sitio, por el hecho de ajustar de forma simultánea el sistema, lo que concuerda con otros trabajos donde analizaron el crecimiento del área basal (Buckman, 1962; Diéguez-Aranda et al., 2005), al no encontrar significativa la incorporación del índice de sitio.
Las ecuaciones de predicción y proyección en diámetro promedio a nivel de rodal (Ec. 5 y 6) fueron esenciales para estimar el área basal. Se considera que el diámetro promedio del rodal es la variable dasométrica más sensible al efecto de la densidad, porque un alto nivel de densidad genera supresión en su crecimiento y un bajo nivel de densidad permite expresar mayor potencial de crecimiento diamétrico. Esto repercute de manera importante en el crecimiento del área basal. Las funciones de crecimiento para esta variable, en particular, consideran: la edad, el número de árboles por hectárea y una medida de la calidad del sitio, como lo es la altura dominante. Esta última variable permite expresar de manera adecuada los niveles de productividad de los rodales de P. patula.
Davis et al. (2001) mencionan que una de las características del diámetro promedio es que este incrementa a través de la vida del rodal cuando el arbolado crece y cuando el arbolado más pequeño dentro del rodal sufre una alta tasa de mortalidad. Contar con modelos para pronosticar el crecimiento en diámetro promedio de masas regulares resulta de utilidad para el manejo forestal, porque esta variable es de primordial interés para la industria forestal. En ese sentido, y de acuerdo con Alder (1980), los modelos de predicción serán más realistas a medida que se incrementen los esfuerzos en la recolección de datos y en la construcción del propio modelo.
Por su parte, las ecuaciones de volumen a nivel de rodal (Ec. 7 y 8) incorporan como variables independientes a la edad, el área basal y la calidad del sitio (expresada mediante la altura dominante o el índice de sitio), las cuales hacen posible la abstracción del fenómeno del rendimiento maderable (Fig. 4). Estas variables se han utilizado convencionalmente para modelar el rendimiento maderable de Pinus arizonica Engl. (Zepeda y Domínguez, 1998), P. rudis Endl. (Magaña et al., 2008), P. patula (Valdez-Lazalde y Lynch, 2000), P. montezumae Lamb. (Zepeda y Acosta, 2000), Cedrela odorata L. y Tabebuia donnell-smithii Rose (Galán et al., 2008).
Torres y Magaña (2001) mencionan que la evaluación de existencias volumétricas en un rodal o plantación permite conocer la cantidad de madera disponible y así poder planificar las actividades de cosecha. Por su parte, Galán et al. (2008) y Magaña et al. (2008) señalan que las ecuaciones de predicción explícita o de rodal completo, permiten estimar la dinámica de crecimiento en volumen por unidad de superficie, y son de gran uso en manejo forestal, debido a su sencillez y precisión. A este respecto, Vanclay (1994) menciona que este tipo de modelos son los más adecuados para la planificación del manejo de rodales coetáneos y plantaciones forestales.
El modelo de mortalidad concuerda con lo señalado por Clutter et al. (1983) y Torres y Magaña (2001), quienes mencionan que en muchos trabajos se ha probado que el IS tiene poca relación dentro de las funciones de mortalidad. Asimismo, coincide con el trabajo de Palahí et al. (2002), quienes proponen esta misma estructura para pronosticar la sobrevivencia en rodales de P. sylvestris L. en el noreste de España. Sin embargo, la tasa de mortalidad anual de estos rodales es de 0.43%, lo cual es explicable siendo sitios experimentales, plantados con densidades iniciales iguales y sujetos a la misma silvicultura. También concuerda parcialmente con lo encontrado por Magaña et al. (2008), quienes presentan una función de mortalidad para rodales naturales de P. rudis Endl., donde la tasa de mortalidad proporcional es una función de la edad y el índice de sitio, para un IS > 20 m, la tasa de mortalidad anual es superior a 5.0 %. Es importante destacar que para realizar pronósticos de rendimiento futuro es necesario establecer algún valor asintótico mínimo, porque si se continúa simulando la mortalidad, esta lleva a estimar cero árboles por hectárea cuando en un bosque bajo manejo esto solo sería posible si ocurre un evento catastrófico. Es decir, la densidad mínima razonable que se puede encontrar en los rodales, para cierta edad, a partir de la cual se acota la mortalidad.
Uso del SCRM
Los turnos técnicos en volumen de alrededor de 20 años calculados con el SCRM actual son similares al turno de 25 años estimado con el SCRM generado por Santiago-García et al. (2013) en la región de estudio. Sin embargo, el acortamiento de la edad de los turnos actuales se debe a predicciones más optimistas del SCRM actual para edades tempranas, es decir, pronostica una mayor velocidad de crecimiento en volumen en edades menores a 20 años. Posterior a esta edad, las predicciones del SCRM actual son más conservadoras respecto al SCRM previo.
De acuerdo con Sánchez et al. (2003), los turnos aumentan según disminuye la calidad del sitio, y la edad del turno disminuye cuando el nivel de densidad del rodal es más bajo o se intensifican los aclareos. Las relaciones fundamentales de crecimiento expresadas en el SCRM permiten corroborar lo anterior.
Por otra parte, con las tablas de rendimiento de densidad variable, es posible evaluar distintos niveles de productividad y densidad, los cuales determinan la capacidad del sitio para alcanzar cierta dimensión en el tamaño del arbolado. Por ejemplo, al cambiar la calidad de sitio y la densidad del rodal, la tabla de rendimiento muestra el crecimiento esperado en diámetro promedio. Esta variable de estado representa un buen indicador de la dimensión de diámetros presentes en el rodal, lo cual resulta de interés para la industria forestal.
Como puede notarse, el SCRM representa una herramienta de manejo poderosa para generar esquemas de manejo maderable y, con ello, tomar decisiones. En ese sentido, su incorporación en los programas de manejo para la región de estudio se hace necesaria. De acuerdo con Vanclay (1994), un SCRM se elabora para: realizar estimaciones confiables de crecimiento y rendimiento corriente y futuro, determinar la edad óptima de cosecha, estimar la producción anual, periódica o total durante el periodo de rotación, realizar análisis financieros, explorar alternativas silviculturales, determinar un régimen de manejo que maximice el volumen maderable o el valor de la producción, entre otras aplicaciones. Por su parte, Pretzsch (2009) señala que los modelos de crecimiento y las simulaciones de crecimiento del bosque juegan un papel importante en manejo forestal, dada la longevidad de los árboles y rodales forestales. Asimismo, menciona que en rodales coetáneos, las tablas de rendimiento pueden ser el mejor enfoque para realizar el manejo forestal, en donde la producción de volumen es el principal objetivo.
La actualización de las ecuaciones de crecimiento permitió ampliar el rango de validez del SCRM, su mejor comportamiento se encuentra en el intervalo de 8 años a 31 años de edad del rodal. Pronósticos fuera de este intervalo deben tomarse con ciertas reservas y es factible, siempre y cuando las variables proyectadas mantengan un comportamiento realista. Mediciones futuras permitirán ampliar el rango de validez de las ecuaciones, así como establecer nuevos patrones de crecimiento y mortalidad natural de los bosques de P. patula en la región de Zacualtipán, Hidalgo. Estas ecuaciones se han integrado al simulador de crecimiento SiCRepp®, el cual permite representar de forma interactiva, infinidad de situaciones en un rodal y así pronosticar su crecimiento y rendimiento, tanto corriente, como futuro (Santiago-García, 2013).
Conclusiones
El sistema de crecimiento y rendimiento actualizado para Pinus patula permite simular un grupo amplio de escenarios silvícolas para el manejo de los rodales repoblados de forma natural en Zacualtipán, Hidalgo. Además, en coincidencia con el sistema previo, el presente ratifica que los turnos utilizados actualmente para el manejo operativo de los bosques de P. patula son demasiado largos (40 años o 50 años) y con intervenciones poco frecuentes, por lo que estos pueden ser acortados para maximizar la producción en volumen total, como la obtención de algún producto específico. En este trabajo se muestra que el insumo básico para realizar pronósticos de crecimiento son los datos de sitios permanentes a nivel de rodal. Con estos modelos de crecimiento y rendimiento se obtienen predicciones y proyecciones de gran precisión, por lo que constituyen una herramienta básica para simular alternativas silviculturales y así seleccionar los regímenes de manejo óptimos de la especie P. patula en la región de estudio.
Referencias
Aguirre-Salado, C.A., J.R. Valdez-Lazalde, H.M. De los Santos-Posadas, G. Ángeles-Pérez, R. Haapanen y A.I. Aguirre-Salado. 2009. Mapeo de carbono arbóreo aéreo en bosques manejados de pino patula en Hidalgo, México. Agrociencia 43(2):209-220. [ Links ]
Assmann, E. 1970. The principles of forest yield study. Pergamon Press. Oxford. 506 p. [ Links ]
Alder, D. 1980. Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos. Vol. 2. Estudio FAO: Montes 22/2. Organización de las Naciones Unidas para la Agricultura y la Alimentación. Roma, Italia. 118 p. [ Links ]
Amaro, A., D. Reed, M. Tomé e I. Themido. 1998. Modelling dominant height growth: Eucalyptus plantations in Portugal. Forest Science 44(1):37-46. [ Links ]
Borders, B.E. 1989. System of equations in forest stand modeling. Forest Science 35(2):548-556. [ Links ]
Borders, B.E. y R. L. Bailey. 1986. A compatible system of growth and yield equations for slash pine fitted with restricted three-stage least squares. Forest Science 32(1):185-201. [ Links ]
Buckman, R. 1962. Growth and yield of red pine in Minnesota. USDA Forest Service, Tech Bull 1272. 50 p. [ Links ]
Cieszewski, C.J. y R.L. Bailey. 2000. Generalized algebraic difference approach: theory based derivation of dynamic site equations with polymorphism and variable asymptotes. Forest Science 46(1):116-126. [ Links ]
Clutter, J.L. 1963. Compatible growth and yield models for loblolly pine. Forest Science 9(3):354-371. [ Links ]
Clutter, J.L., J.C. Forston, L.V. Pienaar, G.H. Brister y R.L. Bailey. 1983. Timber management: A quantitative approach. John Wiley & Sons, Inc. Nueva York. 333 p. [ Links ]
Corral-Rivas, J.J., J.G. Álvarez G., A.D. Ruíz G. y K.V. Gadow. 2004. Compatible height and site index models for five pine species in El Salto, Durango (Mexico). Forest Ecology and Management 201:145-160. [ Links ]
Davis, L.S., K.N. Johnson, P.S. Bettinger y T.E. Howard. 2001. Forest management. 4a ed. McGraw-Hill series in Forest Resources. Nueva York. 804 p. [ Links ]
De los Santos-Posadas, H.M., M. Montero-Mata y M. Kanninen. 2006. Curvas dinámicas de crecimiento en altura dominante para Terminalia amazonia (Gmel.) Excell en Costa Rica. Agrociencia 40(4):521-532. [ Links ]
Diéguez-Aranda, U., F. Castedo D. y J.G. Álvarez G. 2005. Funciones de crecimiento en área basimétrica para masas de Pinus sylvestris L. procedentes de repoblaciones en Galicia. Investigación Agraria: Sistemas y Recursos Forestales 14(2):253-266. [ Links ]
Diéguez-Aranda, U., F. Castedo D., J.G. Álvarez G. y A. Rojo A. 2006a. Dynamic growth model for Scots pine (Pinus sylvestris L.) plantations in Galicia (north-western Spain). Ecological Modelling 191:225-242. [ Links ]
Diéguez-Aranda, U., H.E. Burkhart y R.L. Amateis. 2006b. Dynamic site model for loblolly pine (Pinus taeda L.) plantations in the United States. Forest Science 52(3):262-272. [ Links ]
Galán, L.R., H.M. De los Santos P. y J.I. Valdez H. 2008. Crecimiento y rendimiento maderable de Cedrela odorata I. y Tabebuia donnell-smithii Rose en San José Chacalapa, Pochutla, Oaxaca. Madera y Bosques 14(2):65-82. [ Links ]
García, C.X., H. Ramírez M., C. Rodríguez F., J. Jasso M. y C. A. Ortiz S. 1998. Índice de sitio para caoba (Swietenia macrophylla King) en Quintana Roo, México. Revista Ciencia Forestal en México 23(84):9-19. [ Links ]
García, O. 1988. Growth modeling-a (re)view. New Zealand Journal of Forestry 33(3):14-17. [ Links ]
García, O. 1994. The state-space approach in growth modeling. Canadian Journal of Forest Research 24:1894-1903. [ Links ]
Gómez-Tejero, J., H.M. De los Santos-Posadas, A.M. Fierros-González y J.R. Valdez-Lazalde. 2009. Modelos de crecimiento en altura dominante para Eucalyptus grandis Hill ex Maiden y E. urophylla S. T. Blake en Oaxaca, México. Revista Fitotecnia Mexicana 32(2):161-169. [ Links ]
Kiviste, A., J.G. Álvarez G., A. Rojo A. y A.D. Ruiz G. 2002. Funciones de crecimiento de aplicación en el ámbito forestal. Monografías INIA: Forestal N.° 4. Madrid. 190 p. [ Links ]
Magaña T., O.S., J.M. Torres R., C. Rodríguez F., H. Aguirre D. y A.M. Fierros G. 2008. Predicción de la producción y rendimiento de Pinus rudis Endl. en Aloapan, Oaxaca. Madera y Bosques 14(1):5-19. [ Links ]
Palahí, M., J. Miina, M. Tomé y G. Montero. 2002. Stand-level yield model for Scots pine (Pinus sylvestris L.) in northeast Spain. Investigación Agraria: Sistemas y Recursos Forestales 11(2):409-424. [ Links ]
Pretzsch, H. 2009. Forest dynamics, growth and yield: From measurement to model. Springer-Verlag. Berlín, Heidelberg. Alemania. 664 p. [ Links ]
Ramírez, M.H., R.L. Bailey y B.E. Borders. 1987. Some implications of the algebraic difference method approach for developing growth models. In: Forest Growth Modeling and Prediction. IUFRO. Minneápolis, EUA. [ Links ]
Rodríguez-Acosta, M. y B. Arteaga-Martínez. 2005. Índice de sitio para Pinus chiapensis (Martínez) Andresen, en los estados de Veracruz y Puebla, México. Revista Chapingo Serie Ciencias Forestales y del Ambiente 11(1):39-44. [ Links ]
Sánchez, F., R. Rodríguez, A. Rojo, J.G. Álvarez, C. López, J. Gorgoso y F. Castedo. 2003. Crecimiento y tablas de producción de Pinus radiata D. Don en Galicia. Investigación Agraria: Sistemas y Recursos Forestales 12(2):65-83. [ Links ]
Santiago-García, W., H.M. De los Santos-Posadas, G. Ángeles-Pérez, J.R. Valdez-Lazalde y G. Ramírez-Valverde. 2013. Sistema compatible de crecimiento y rendimiento para rodales coetáneos de Pinus patula. Revista Fitotecnia Mexicana 36(2):163-172. [ Links ]
Santiago-García, W. 2013. Simulador de crecimiento para el manejo de rodales coetáneos de Pinus patula. Tesis de Doctorado en Ciencias. Colegio de Postgraduados. Montecillo, Texcoco, México. 109 p. [ Links ]
SAS Institute Inc. 2011. SAS/ETS® 9.3 User's Guide. Cary, NC: SAS Institute Inc. [ Links ]
Schumacher, F.X. 1939. A new growth curve and its application to timber-yield studies. Journal of Forestry 37:819-820. [ Links ]
Sullivan, A.D. y J.L. Clutter. 1972. A simultaneous growth and yield model for loblolly pine. Forest Science 18(1):76-86. [ Links ]
Torres R., J.M. y O.S. Magaña T. 2001. Evaluación de plantaciones forestales. Limusa. México. 472 p. [ Links ]
Valdez-Lazalde, J.R. y T.B. Lynch. 2000. Merchantable and total volume equations for thinned natural stands of patula pine. Agrociencia 34(6):747-758. [ Links ]
Vanclay, J.K. 1994. Modelling forest and yield, applications to mixed tropical forests. CAB International. Dinamarca. 312 p. [ Links ]
Vargas-Larreta, B., J.G. Álvarez-González, J.J. Corral-Rivas y Ó.A. Aguirre C. 2010. Construcción de curvas dinámicas de índice de sitio para Pinus cooperi Blanco. Revista Fitotecnia Mexicana 33(4):343-351. [ Links ]
Zepeda B., E.M. y A. Domínguez P. 1998. Niveles de incremento y rendimiento maderable de poblaciones naturales de Pinus arizonica Engl., de El Poleo, Chihuahua. Madera y Bosques 4(1):27-39. [ Links ]
Zepeda B., E. M. y M. Acosta M. 2000. Incremento y rendimiento maderable de Pinus montezumae Lamb., en San Juan Tetla, Puebla. Madera y Bosques 6(1):15-27. [ Links ]
Zhao, D., B. Borders, M. Wang y M. Kane. 2007. Modeling mortality of second-rotation loblolly pine plantations in the Piedmont/Upper Coastal Plain and Lower Coastal Plain of the southern United States. Forest Ecology and Management 252:132-143. [ Links ]
Nota
Este documento se debe citar como: Santiago-García, W., H.M. De los Santos-Posadas, G. Ángeles-Pérez, J.R. Valdez-Lazalde, J.J. Corral-Rivas, G. Rodríguez-Ortiz y E. Santiago-García. 2015. Modelos de crecimiento y rendimiento de totalidad del rodal para Pinus patula. Madera y Bosques 21(3):95-110.














