Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias geológicas
versión On-line ISSN 2007-2902versión impresa ISSN 1026-8774
Rev. mex. cienc. geol vol.23 no.3 Ciudad de México ene. 2006
Revista mexicana de ciencias geológicas
Critical values for 22 discordancy test variants for outliers in normal samples up to sizes 100, and applications in science and engineering
Surendra P. Verma1 and Alfredo Quiroz–Ruiz2
1 Centro de Investigación en Energía, Universidad Nacional Autónoma de México, Priv. Xochicalco s/no., Col Centro, Apartado Postal 34, 62580 Temixco, Morelos, Mexico
E–mail: spv@cie.unam.mx
2 Centro de Investigación en Energía, Universidad Nacional Autónoma de México, Priv. Xochicalco s/no., Col Centro, Apartado Postal 34, 62580 Temixco, Morelos, Mexico
Manuscript received: March 18, 2006
Corrected manuscript received: August 9, 2006
Manuscript accepted: August 23, 2006
ABSTRACT
In this paper, the modifications of the simulation procedure as well as new, precise, and accurate critical values or percentage points (for the majority of data with four decimal places; respective average standard error of the mean ˜0.0001–0.0025) of nine discordancy tests, with 22 test variants, and each with seven significance levels α = 0.30, 0.20, 0.10, 0.05, 0.02, 0.01, and 0.005, for normal samples of sizes n up to 100 are reported. Prior to our work, only less precise critical values were available for most of these tests, viz., with one (for n < 20) and three decimal places (for greater n) for test N14; two decimal places fortests N2, N3–k=2,3,4, N6, and N15; and three decimal places for N1, N4–k=3,4, N5, and N8; but all of them with unknown errors. In fact, the critical values were available for n only up to 20 for test N2, up to 30 for test N8, and up to 50 for N4–k=1,3,4, whereas for most other tests, in spite of the availability for n up to 100 (or more), interpolations were required because tabulated values were not reported for all n in the range 3–100. Therefore, the applicability of these discordancy tests is now extended up to 100 observations of a particular parameter in a statistical sample, without any need of interpolations. The new more precise and accurate critical values will result in a more reliable application of these discordancy tests than has so far been possible. Thus, we envision that these new critical values will result in wider applications of these tests in a variety of scientific and engineering fields such as agriculture, astronomy, biology, biomedicine, biotechnology, chemistry, electronics, environmental and pollution research, food science and technology, geochemistry, geochronology, isotope geology, meteorology, nuclear science, paleontology, petroleum research, quality assurance and assessment programs, soil science, structural geology, water research, and zoology. The multiple–test method with new critical values proposed in this work was shown to perform better than the box–and–whisker plot method used by some researchers. Finally, the so–called "two standard deviation" method frequently used for processing inter–laboratory databases was shown to be statistically–erroneous, and should therefore be abandoned. Instead, the multiple–test method with 15 tests and 33 test variants, all of which now readily applicable to sample sizes up to 100, should be used. To process inter–laboratory databases, our present approach of multiple–test method is also shown to perform better than the "two standard deviation " method.
Keywords: outlier methods, normal sample, two standard deviation method, 2s, reference materials, Monte Carlo simulations, critical value tables, Dixon Q–test, skewness, kurtosis, petroleum hydrocarbon.
RESUMEN
En este trabajo se reportan las modificaciones del procedimiento de la simulación así como valores críticos o puntos porcentuales nuevos y más precisos y exactos (para la mayoría de los datos con cuatro puntos decimales; el error estándar de la media ˜0.0001–0.0025) para nueve pruebas de discordancia con 22 variantes, y cada una con siete niveles de significancia α = 0.30, 0.20, 0.10, 0.05, 0.02, 0.01 y 0.005, para muestras normales con tamaño n hasta 100. Antes de nuestro trabajo, solamente se disponía de valores críticos menos precisos para la mayoría de estas pruebas, viz., con uno (para n < 20) y tres puntos decimales (para n mayores) para la prueba N14, dos puntos decimales para las pruebas N2, N3–k=2,3,4, N6 y NI5, y tres puntos decimales para NI, N4–k=3,4, N5 y N8, pero todos ellos con errores desconocidos. En realidad se disponía de los valores críticos solamente para n hasta 20 para la prueba N2, hasta 30 para la prueba N8, y hasta 50 para N4–k=1,3,4, mientras que para muchas otras pruebas, a pesar de la disponibilidad para hasta n 100 (o más) se requería de interpolaciones, dado que los valores tabulados no fueron reportados para todos los n en el intervalo de 3 a 100. Por consecuencia, la aplicabilidad de las pruebas de discordancia es extendida hasta 100 observaciones de un determinado parámetro en una muestra estadística, sin necesidad de realizar las interpolaciones de los valores críticos. Los valores críticos nuevos y más precisos y exactos resultarán en una aplicación más confiable de las pruebas de discordancia que ha sido posible hasta ahora. De esta manera, consideramos que estos nuevos valores críticos resultarán en aplicaciones más amplias de estas pruebas en una variedad de campos de conocimiento científico y de ingenierías, tales como agricultura, astronomía, biología, biomedicina, biotecnología, ciencia del suelo, ciencia nuclear, ciencia y tecnología de los alimentos, contaminación ambiental, electrónica, geocronología, geología estructural, geología isotópica, geoquímica, investigación del agua, investigación del petróleo, meteorología, paleontología, programas de aseguramiento de calidad, química y zoología. El método de pruebas múltiples con nuevos valores críticos propuesto aquí proporciona mejores resultados que el método de la gráfica de "boxy whisker" usado por algunos investigadores. Finalmente, se demostró que el así llamado método de "dos desviaciones estándar", frecuentemente usado para procesar las bases de datos interlaboratorios, es erróneo y, por lo tanto, debe ser abandonado. En su lugar debe usarse el método de pruebas múltiples con 15 pruebas y 33 variantes, todas ellas ahora rápidamente aplicables para los tamaños de muestras hasta 100. Nuestro procedimiento de pruebas múltiples parece funcionar mejor que el método de "dos desviaciones estándar" para el procesamiento de datos geoquímicos provenientes de muchos laboratorios.
Palabras clave: métodos de valores desviados, muestra normal, prueba de dos desviaciones estándar, 2s, materiales de referencia, simulaciones Monte Cario, tablas de valores críticos, prueba Q de Dixon, sesgo, curtosis, hidrocarburos de petróleo.
INTRODUCTION
In a recent paper (Verma and Quiroz–Ruiz, 2006), we covered the following points: (1) explained the need of new critical values or percentage points of statistical tests for normal univariate samples; (2) developed and reported a highly precise and accurate Monte Carlo type simulation procedure for N(0,l) random normal variates; (3) presented new, precise, and accurate critical values for seven significance levels α = 0.30, 0.20, 0.10, 0.05, 0.02, 0.01, and 0.005, and for sample sizes n up to 100 for six Dixon discordancy tests (with 11 test variants) for normal univariate samples; and (4) highlighted the use of these new values in very diverse fields of science and engineering, including the Earth Sciences. We had included all six frequently used discordancy tests (N7 and N9–N13; see pp. 218–236 of Barnett and Lewis, 1994), initially proposed by Dixon (1950,1951,1953), for simulating new, precise, and accurate critical values for n up to 100 (number of data in a given statistical sample, n = 3(1)100 for test N7, i.e., for all values of n between 3 and 100; n = 4(1)100 for tests N9 and N11; n = 5(1)100 for tests N10 and N12; and n = 6(1)100 for test N13).
It is pertinent to mention that researchers (e.g., Dybczyñski et al, 1979; Dybczyñski, 1980; Barnett and Lewis, 1994; Verma, 1997,1998,2005; Verma et al, 1998; Velasco et al, 2000; Guevara et al, 2001; Velasco–Tapia et al, 2001) have recommended that most, if not all the available discordancy tests should be applied to a given data set to detect discordant outliers. Because the critical values for the six Dixon tests have now been significantly improved and extended (Verma and Quiroz–Ruiz, 2006), there is still the need for improving the existing critical values and simulating new ones for the remaining tests for normal samples listed by Barnett and Lewis (1994).
It is also important to note that we are dealing with tests for normal univariate samples, i.e., the statistical sample is assumed to be drawn from a normal population. Obviously, different sets of critical values would be required for other types of distributions such as exponential or Poisson distributions (see Barnett and Lewis, 1994, or Zhang, 1998, for more details).
In the present work, for simulating new, precise, and accurate critical values for the same seven significance levels (α = 0.30 to 0.005) and for n up to 100, we have included most of the remaining tests for normal univariate samples (nine tests with 22 test variants): N1 (upper or lower version), N2 (two–sided), N3–k=2,3,4 (upper or lower), N4–k=1,2,3,4 (upper or lower), N5–k=2 (upper–lower pair), N6–k=2 (upper–lower pair), N8 (two–sided; also known as Dixon Q–test), N14 (skewness or third moment test), and N15 (kurtosis or fourth moment test); see pp. 218–236 of Barnett and Lewis (1994), orpp. 89–97 of Verma (2005). The new critical values are compared with the literature values and are shown to be more precise and accurate, enabling thus statistically more reliable applications in many science and engineering fields. We also present a few examples for the application of all normal univariate tests for which we have reported new critical values in this as well as in our earlier paper (Verma and Quiroz–Ruiz, 2006).
DISCORDANCY TESTS
We will not repeat the explanation of discordancy tests; the reader is referred to Barnett and Lewis (1994), Verma (2005), or our earlier paper (Verma and Quiroz–Ruiz, 2006). The nine tests with their 22 variants for which critical values were simulated are listed in Table 1. We note that critical values were available in the literature only for n up to 20 for test N2, up to 30 for N8, and up to 50 for N4–k=1,3,4, whereas for most other tests, in spite of the availability for n up to 100 (or more), interpolations were occasionally required because tabulated values were not reported for all n (see Barnett and Lewis, 1994, or tables A4 to A18 in Verma, 2005).
Tests N1 and N2
We will briefly describe discordancy tests Nl and N2, which are, respectively, the upper (or lower) and extreme outlier tests in a normal sample with both population mean (µ) and population variance (σ2) unknown (Barnett and Lewis, 1994), because their statistically "erroneous" version has been used as a popular, so–called "two standard deviation" method by numerous workers (e.g., Stochand Steele, 1978; Ando et al., 1987, 1989; Gladney and Roelandts, 1988, 1990; Gladney et al., 1991, 1992; Itohetal, 1993; Imai et al., 1995, 1996) to process inter–laboratory data for international geochemical reference materials.
The test statistic of Nl for upper or lower outlier is, respectively:
 .......................................................................(1)
.......................................................................(1)
or
 ........................................................................(2)
........................................................................(2)
whereas that of N2 is
 ........................................................(3)
........................................................(3)
Here, for an ordered array x(1), x(2), x(3),... x(n–2), x(n–1), x(n)of n observations x(1) is the lowest observation and x(n) the highest one;  is the sample mean; and s is the sample standard deviation.
is the sample mean; and s is the sample standard deviation.
Two standard deviation method: a statistically erroneous and outdated version of tests N1 and N2
For the standard normal distribution, the total probability of observations at a distance greater than l.96σ (i.e., about 2σ) from the mean µ, i.e., outside the (µ ± 1.96σ) is 0.05, in other words, about 95% of the area of the density curve is contained within this range (e.g., Otto, 1999). These considerations of the normal density curve have been used by some workers to fix the limit of 2σ, or more appropriately 2s (because the population parameters µ and σ are not known for most experimental data) for testing samples of finite size for discordant outliers, i.e., observations falling within ( ±2s) are retained and those outside this range are rejected, irrespective of the actual value of n (where n,
±2s) are retained and those outside this range are rejected, irrespective of the actual value of n (where n,  , and s are, respectively, the total number of samples, location parameter – sample mean, and scale parameter – sample standard deviation).
, and s are, respectively, the total number of samples, location parameter – sample mean, and scale parameter – sample standard deviation).
This kind of outlier test belongs to a group of old, outdated test procedures (pre–1925!) characterized by two general defects (see for more details pages 30–31,108–116, and 222–223 in Barnett and Lewis, 1994): they fail to distinguish between population variance (σ) and sample variance (s), and, more importantly, they are erroneously based on the distributional behavior of a random sample value rather than on an appropriate sample extreme value. Barnett and Lewis (1994, p. 31) go on stating that even a more serious shortcoming of such an outdated procedure is "the failure to recognize that it is an extreme x(1) or x(n) which (by the very nature of outlier study) should figure in the test statistic, rather than an arbitrary sample value xj". This shortcoming is certainly overcome by tests Nl or N2 above (see equations 1 to 3), in which an extreme value (x(1) or x(n)) is tested by the respective test statistic. Thus, an ad hoc procedure of a "fixed multiple of standard deviation" leads to rejection of any observation xj for which  is sufficiently large, in fact, >2 for the 2s method or >3 for the 35 method –but with no regard to the effect of sample size n on the distribution form of the statistic. We will further comment on the shortcomings of this procedure after we have presented the new critical values for tests N1 and N2.
is sufficiently large, in fact, >2 for the 2s method or >3 for the 35 method –but with no regard to the effect of sample size n on the distribution form of the statistic. We will further comment on the shortcomings of this procedure after we have presented the new critical values for tests N1 and N2.
Masking and swamping effects and different types of test statistics
We will briefly point out the reasons for our recommendations to apply all outlier tests to a given data set instead of only a few of them (see Verma, 1997,1998; Verma et al., 1998 for more details).
One problem in testing for a single outlier in a normally distributed sample is the sensitivity to the phenomenon of masking (Bendre and Kale, 1987; Barnett and Lewis, 1994). A discordancy test of the most extreme observation (e.g., xn) is rendered insensitive by the proximity of the next most extreme observation (xn–1), in which case the presence of the latter would have masked the first. Dixon test N7 is especially susceptible to such masking effects (see Verma and Quiroz–Ruiz, 2006, for the test statistic TNI), although the Nl statistic (Grubbs, 1950) is probably not too much better. One solution to this problem is to use test statistics that are less sensitive to masking. There are a number of Dixon–like statistics for this purpose (N11–N13; Barnett and Lewis, 1994; Verma and Quiroz–Ruiz, 2006). In the case of test N12, for example, the numerator is the difference between the outlier (xn or x1) being tested and its second–nearest neighbor (xn–2or x3). No masking effect is observed by the measurement value xn–1 or x2.
Outlier masking occurs because there are actually two (or more) outliers, and some statistics, such as Nl, work best when testing data sets with a single outlier (e.g., Prescott, 1978). If a data set contains more than one outlier, it is necessary to modify the statistical approach, considering the next outlier assemblages: (1) two or more upper outliers, (2) two or more lower outliers, and (3) a combination of one (or more) upper outlier(s) and one or more lower outlier(s). Caution is, however, required if one is dealing with chemical data obtained from different analytical techniques, in which case other statistical tests, such as F–test, Student t, or ANOVA, should, in fact, be applied prior to the application of discordancy tests (see, e.g., Verma, 1998, 2005). This topic will be dealt with in more detail in a separate paper.
In general, two testing approaches have been applied for these cases (Barnett and Lewis, 1994): (1) the consecutive testing approach, where a test statistic such as Nl or N7 is applied repeatedly to a data set (one outlier at a time); or (2) the block testing approach, where a statistic simultaneously tests k (= 2, 3, 4, or more) observations in the data set.
In the consecutive testing, the most extreme outlier is evaluated; if it gives a positive test result, i.e., if this outlier is declared to be discordant, it is removed from the data set, and then the most extreme remaining outlier is tested. This procedure is repeated until all the outliers are tested, or until an outlier gives a negative test result, i.e., it is not discordant. However, the disadvantage is the susceptibility of this procedure to masking effects. Tests N1 and N7 are certainly poor candidates for this type of testing procedure although tests N14 and N15 (high–order moment tests) should be applied consecutively when more than one outlier is present in a statistical sample (see Barnett and Lewis, 1994). Test N14 was recommended for a one–sided detection, although Iglewicz and Martinez (1982) reported that this test is greatly affected by masking effect, and thus should not be used when more than one outlier is suspected. Both tests N14 and N15 are used for testing an extreme value (two–sided tests). The poor efficiency of these consecutive tests based on the use of standard deviation (s), such as Nl or N2, can be adduced to the fact that value of s is greatly influenced by the presence of discordant outliers. As a consequence, the presence of several outliers may cause a sufficiently large increase in standard deviation, with the result that no outliers are detected (Barnett and Lewis, 1994).
An alternative to consecutive testing is block testing, where a statistic is used to test all k outliers at once (e.g., test N3 orN4; Table 1). Also, some differences in performance have been reported for block–testing statistics (Prescott, 1978; Hayes and Kinsella, 2003). For example, McMillan (1971) suggested that test N4–k=2 is more robust than test N3–k=2. It is important to point out that, assuming that all outliers have been identified, statistics intended for block tests are not susceptible to outlier masking. However, the application of this procedure could generate another problem, known as outlier swamping (Barnett and Lewis, 1994). A block test could be insensitive if the second observation xn–1 is close to the next neighbor (xn–2) and is not outlying or discordant. The pair xn, xn–1 might not reach discordancy level when tested jointly, even though xn on its own is discordant in relation to the other n–1 observations (i.e., swamping effect of xn–1). In block testing, all k outliers are labeled as contaminants. What this means in practice is that contaminants belong to a different probability distribution than the rest of the data or they are accepted as "normal" deviated measurements drawn from a different normal distribution. There is no middle ground, as there is in consecutive testing, where it is possible to establish when some outliers are contaminants and when some are not. Thus, there is the possibility that a marginal outlier might be falsely declared a contaminant because it is "carried along" in the block testing procedure by others, more extreme, outliers. Or perhaps a few marginal outliers cause the block testing procedure to fail, which means that the contaminants that are in the block will not be identified. However, some procedures have been proposed to establish k (i.e., the number of contaminants in the sample), free from the masking and swamping effects, when testing upper or lower outliers (Zhang and Wang, 1998). The block testing procedure can also be applied consecutively if more that k outliers are suspected in a given data set.
In summary, more work is needed to better understand the relative merits and usefulness of different test procedures. As pointed out in our earlier paper (Verma and Quiroz–Ruiz, 2006), these evaluations can also be performed empirically or through computer simulations, which is planned to be carried out in a future study. From the practical point of view, however, we can evaluate an experimental data set, using both types of outlier tests –single–outlier (consecutive procedure) as well as multiple–outlier (block procedure) tests– termed here as the "multiple–test" method.
SIMULATION PROCEDURE FOR MORE PRECISE AND ACCURATE CRITICAL VALUES
Our highly precise and accurate Monte Carlo type simulation procedure has already been described in detail (Verma and Quiroz–Ruiz, 2006) and, therefore, will not be repeated here. However, some required changes will be mentioned.
As in our earlier work, our simulations were of sizes 100,000, and were repeated 10 times (each using a different set of 10,000,000 random normal variates) for obtaining the final mean critical value or percentage point and its standard error. However, for test Nl, two independent test statistics (one for upper and the other for lower outlier) were simulated and thus 20 independent results couldbe obtained from the same simulation scheme as reported earlier (Verma and Quiroz–Ruiz, 2006). Similarly, because of the availability of the upper or lower version of the statistic (Table 1), 20 results of critical values were obtained for tests N3–k=2,3,4, and N4–k= 1,2,3,4.
Barnett and Lewis (1994; pp. 218–221) have shown that the statistics TN1(u)=(x(n)–  )/s and TN4(1u)=S2n)/S2 are really equivalent (forthe meaning of S2n and S2 see pp. 95–96 of Verma, 2005), and bear the following relationships:
)/s and TN4(1u)=S2n)/S2 are really equivalent (forthe meaning of S2n and S2 see pp. 95–96 of Verma, 2005), and bear the following relationships:
 ...........................................................(4)
...........................................................(4)
and conversely,
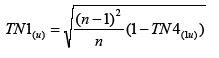 .......................................................(5)
.......................................................(5)
Similar equations are valid for lower outlier statistics TN1(l)and TN4(1l).
The above exact relationships enable us to use the simulation results of TN1(1u) and TN4(1l) to convert them, respectively, for those of TN1(u) and TN1(l), and vice versa. In this way, we obtained 20 more results of critical values from simulations of sizes 100,000 for tests Nl and N4–k=l. Due to the above exact relationships and in order to avoid the "artificial" decrease of standard errors of the mean critical values, we used different starting points (either the first or the second datum in a given simulated normal distribution) for drawing samples of sizes up to 100 (for tests Nl and N4–k=l) from the simulated normal independently and identically distributed IID N(0,l) distributions (see more details in Verma and Quiroz–Ruiz, 2006, and references cited therein).
Thus, in summary, the critical values for tests N1 and N4–k=1 were from 40 simulations of sizes 100,000; for tests N3–k=2,3,4 and N4–k=2,3,4 from 20 such simulations; and for tests N2, N5, N6, N8, N14, and N15 from 10 such simulations.
However, for tests N2, N6, and N15, the standard errors of the mean critical values obtained from 10 simulations of sizes 100,000 were still large (the standard error was generally on the third decimal place, and was the highest for test N15 that involves a fourth order statistic, see the definition of 77V15 in Table 1). Therefore, we decided to simulate these critical values from 10 simulations, but each of sizes 500,000 (five times greater than the sizes used by Verma and Quiroz–Ruiz, 2006), for which 10 different sets of 50,000,000 random normal variates had to be generated. In fact, for tests N6 and N15 we carried out a total of 20 simulations each of sizes 500,000. Twenty instead of 10 simulations were made possible by varying the starting point for a given set of IID N(0,1) while drawing samples of sizes up to 100.
The final critical values tabulated correspond to the largest simulation sizes for each test. These are: 100,000 for N3–k=2,3,4, N4–k=2,3,4, N5, N8, and N14; and 500,000 for N1, N4–k=1, N2, N6, andN15. The mean( ) and standard error of the mean
) and standard error of the mean 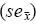 of all individual simulation results for each n and α were estimated and the best results (with the smallest errors) reported in tabular form. The median critical values were found to be in close agreement with these mean values, ascertaining the simulated critical values to be also normally distributed.
of all individual simulation results for each n and α were estimated and the best results (with the smallest errors) reported in tabular form. The median critical values were found to be in close agreement with these mean values, ascertaining the simulated critical values to be also normally distributed.
RESULTS OF NEW CRITICAL VALUES
The new critical values for 22 discordancy test variants (Table 1), for each n from 3 (or 4, 5,6,7, 8, or 9, depending on the type of statistic to be calculated) up to 100 and α= 0.30, 0.20, 0.10, 0.05, 0.02, 0.01, and 0.005 (corresponding to confidence level of 70% to 99.5%, or equivalently significance level of 30% to 0.5%) are summarized in Tables A1–A14, available from the journal web site (electronic supplement 23–3–01). The footnotes in these tables also present the standard error of the mean 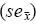 for these critical values. Thus, for all cases our present values are more reliable (error is on the fourth or even the fifth decimal place, although in some cases a small number –1 or 2– on the third decimal place) than the earlier literature values (compiledby Barnett and Lewis, 1994; and Verma, 2005; see also Pearson and Hartley, 1976). In fact, the errors of these literature values are never precisely known. The errors of our present simulations for all values of a ranged as follows: ˜0.0006–0.0011 fortest N1 (Table A1); ˜0.0002–0.0010 for test N2 (Table A2), ˜0.0002–0.0009 for N3–k=2 (Table A3); ˜0.0002–0.0010 for N3–k=3 (Table A4); ˜0.0003–0.0010 for N3–k=4 (Table A5); ˜0.00002–0.0001 for N4–k=1 (Table A6; note most errors on the fifth decimal place); ˜0.00007–0.0003 for N4–k=2 (Table A7; note some errors on the fifth decimal place); ˜0.00008–0.0003 for N4–k=3 (Table A8; note some errors on the fifth decimal place); ˜0.00007–0.0003 for N4–k=4 (Table A9; note some errors on the fifth decimal place); ˜0.00008–0.0004 for N5–k=2 (Table A10; note some errors on the fifth decimal place); ˜0.0002–0.0008 for N6–k=2 (Table A11);–0.0001–0.0005 for N8 (Table A12); ˜0.0002–0.0009 for N14 (Table A13); and ˜0.0002–0.0025 for N15 (Table A14).
for these critical values. Thus, for all cases our present values are more reliable (error is on the fourth or even the fifth decimal place, although in some cases a small number –1 or 2– on the third decimal place) than the earlier literature values (compiledby Barnett and Lewis, 1994; and Verma, 2005; see also Pearson and Hartley, 1976). In fact, the errors of these literature values are never precisely known. The errors of our present simulations for all values of a ranged as follows: ˜0.0006–0.0011 fortest N1 (Table A1); ˜0.0002–0.0010 for test N2 (Table A2), ˜0.0002–0.0009 for N3–k=2 (Table A3); ˜0.0002–0.0010 for N3–k=3 (Table A4); ˜0.0003–0.0010 for N3–k=4 (Table A5); ˜0.00002–0.0001 for N4–k=1 (Table A6; note most errors on the fifth decimal place); ˜0.00007–0.0003 for N4–k=2 (Table A7; note some errors on the fifth decimal place); ˜0.00008–0.0003 for N4–k=3 (Table A8; note some errors on the fifth decimal place); ˜0.00007–0.0003 for N4–k=4 (Table A9; note some errors on the fifth decimal place); ˜0.00008–0.0004 for N5–k=2 (Table A10; note some errors on the fifth decimal place); ˜0.0002–0.0008 for N6–k=2 (Table A11);–0.0001–0.0005 for N8 (Table A12); ˜0.0002–0.0009 for N14 (Table A13); and ˜0.0002–0.0025 for N15 (Table A14).
As for our earlier tables for the six Dixon tests (Verma and Quiroz–Ruiz, 2006), these new critical value data, along with their individual uncertainty estimates, are available in other formats such as txt or Excel or Statistica, on request from any of the authors (S.P. Verma spv@cie.unam.mx, or A. Quiroz–Ruiz aqr@cie.unam.mx).
In spite of this important observation, i.e., our simulation results being more precise than the earlier literature values, we decided to compare the literature critical values for the most commonly used α = 0.05 (5% SL) and 0.01 (1% SL) with our results to highlight the similarities and differences between the two sets. These comparisons are graphically presented in: Figure 1 for single–outlier tests N1, N2, N4–k=1, N8, N14, and N15; Figure 2 for two multiple–outlier tests N3–k=2,3,4 and N4–k=2,3,4; and Figure 3 for the remaining two multiple–outlier tests N5–k=2 and N6–k=2. The differences between our newly simulated critical values and the literature data (Figures 1, 2, 3) are as follows (listed in ascending order of these differences): up to –0.15% for test N1, ˜0.2% for test N6(k=2), ˜0.4% for tests N2 and N3–k=4, ˜0.7% for test N3–k=3, ˜0.8% for test Nl 5, –1% for tests N3–k=2, N4–k= 1, and N4–k=2, ˜2% for test N8, ~6% for test N4–k=3, ˜8% for test N14, ˜15% for test N4–k=4, and ˜20% for test N5(k=2).
These differences are generally larger for 1% SL (99% CL, or α = 0.01) values than for 5% SL (95% CL, or α = 0.05). We attribute these differences to the inaccuracy of literature values (some of them were generated by just one simulation of small sizes of 10,000 only; for others, simulation procedure was not specified) as compared to the present work based on 10 to 40 independent simulations of very large sizes (from 100,000 requiring 10,000,000 random normal variates and IID N(0,l) values to 500,000 requiring 50,000,000 random normal variates and IID N (0,1) values).
For single–outlier test Nl there seem to be small systematic differences for 1% SL values for n >50 (Figure 1a) between our values and the literature values (Grubbs and Beck, 1972); for these sizes (n >50), the literature values are systematically somewhat greater than our new simulated values.
The less–precise literature values for another single–outlier test N2 (available for n only up to 20) differ from our new values by < 0.4% (Figure 1b).
For multiple–outlier test N3 the differences between our newly simulated values and the literature are somewhat larger, up to about 1% for the k=2 variant (Figure 2a), about 0.7% for k=3 (Figure 2b), and about 0.4% for k=4 (Figure 2c). This may be due to the fact that the literature values were generated from a single simulation of sizes 10,000 (Barnett and Lewis, 1994) –much smaller than our present simulations of sizes 500,000 repeated up to 20 times. These differences are even larger than the assumed minimum error of ±0.01 shown as blue–dashed and red–dotted lines in Figure 2 (see numerous %Difference symbols fall above or below these curves).
For multiple–outlier test N4 these differences are still larger than for tests Nl to N3, up to about 1.1 for the k = l (single–outlier version of test N4) and k = 2 variants (Figures 1c and 2d), up to about 6% for k = 3 (Figure 2e), and up to about 15% for k = 4 (Figure 2f).
For multiple–outlier test N5–k=2, the differences of up to 20% (Figure 3a) are due to much smaller sizes of 10,000 for the literature critical values (Barnett and Lewis, 1994).
For multiple–outlier test N6–k=2, on the other hand, very small differences of up to about 0.2% (Figure 3b) were observed; the reason for such a close agreement is not clear.
For single–outlier Dixon–type test N8 (King, 1953), also known as Dixon Q–test, the differences are generally quite large, reaching up to about 2%. This is because the literature values were simulated using small sizes of 10,000.
Single–outlier tests N14 (skewness) and N15 (kurtosis) are specially recommended to be used consecutively (Barnett and Lewis, 1994). Although for test N14 the differences reach up to about 8%, most critical values for n >20 differ only by a much smaller amount (Figure 1e).
Finally, for single–outlier test N15, the differences are relatively small (up to ˜0.8%; Figure 1f).
APPLICATIONS IN SCIENCE AND ENGINEERING
The tests (Table 1) after extending their applicability to samples of sizes up to 100, canbe applied to all examples earlier summarized by us (Verma and Quiroz–Ruiz, 2006). These include: (1) Agricultural and Soil Sciences (Stevens et al, 1995; Batjes, 2005; Lugo–Ospina et al., 2005; Luedeling et al., 2005); (2) Aquatic environmental research (Thomulka and Lange, 1996); (3) Astronomy (Taylor, 2000); (4) Biology (Linkosalo etal, 1996; Schaberand Badeck, 2002); (5) Biomedicine and Biotechnology (Freeman et al., 1997; Woitge et al, 1998; Sevransky etal, 2005); (6) Chemistry (Zaric and Niketic, 1997); (7) Electronics (Jakubowska and Kubiak, 2005); (8) Ecology (Yurewicz, 2004); (9) Geochronology (Bartlett et al, 1998; Wang et al, 1998; Dougherty–Page and Bartlett, 1999); (10) Geodesy (Kern et al, 2005); (11) Geochemistry (Treviño–Cázares et al, 2005); (12) Isotope Geology (Morán–Zenteno etal, 1998); (13) Medical science and technology (Tigges et al, 1999; Hofer and Murphy 2000; Reed et al., 2002; Stancak et al., 2002; Cooper et al, 2006); (14) Meteorology (Graybeal et al, 2004); (15) Paleontology (Alberdi and Corona–M., 2005; Esquivel–Macias et al, 2005; Ifrim et al, 2005; Villaseñor et al, 2005); (16) Petroleum hydrocarbons and organic compounds in sediment samples (Villeneuve et al., 2002); (17) Quality assurance and assessment programs in Biology and Biomedicine (Ihnat, 2000; Patriarca et al, 2005), in cement industry (Sieber et al, 2002), in Food Science and Technology (In't Veld, 1998: Suhren and Walte, 2001; Langton et al, 2002; Morabito et al, 2004; Villeneuve et al, 2004), in Environmental and Pollution Research (Dybczyñski et al., 1998; Gill et al., 2004), in Nuclear Science (Lin et al., 2001), in Rock Chemistry (Velasco–Tapia et al., 2001; Lozano and Bernal, 2005), in Soil Science (Hanson et al, 1998; Verma et al., 1998), and in Water Research (Holcombe et al, 2004); (18) Structural Geology (Dávalos–Álvarez et al, 2005); (19) Water Resources (Buckley and Georgianna, 2001); and (20) Zoology (Harcourt et al, 2005).
Further, as was suggested by Shoemaker et al. (1996) for the Dixon tests, our new critical value tables will be equally useful for applying these discordancy tests for identifying outliers in linear regressions such as those employed by: Verma (2006) for trace element inverse modeling; Guevara et al. (2005) and Santoyo et al. (2006) for instrumental calibration purposes; and Verma et al. (2006) for fluid chemistry and geotermometric temperatures.
Users of a number of internet sites (e.g., SCNPHT, 2006; WORM Database, 2006; and ESMP, 2006) will also benefit from the incorporation of these new tables of critical values and the respective tests into these systems.
Specific examples
We now present a number of examples or case histories to illustrate the use of all discordancy tests for which new critical values have been obtained in this work and by Verma and Quiroz–Ruiz (2006). We have designed and used a Statistica spreadsheet to apply all 15 tests (Nl to N15) with 33 test variants. A computer program is currently under preparation for an easy use of our multiple–test method. For these applications, we chose the strict confidence level of 99% (i.e., we used the 99% CL, or 1% SL, or 0.01 α n; see the respective critical values in Tables A1–A14 in the electronic supplement to present work; and tables 2–7 of Verma and Quiroz–Ruiz, 2006).
Example 1: Petroleum hydrocarbons in a sediment reference sample
We used the example of IAEA–417 (IAEA–International Atomic Energy Agency) used by Villeneuve et al. (2002) for an inter–laboratory study to highlight our multiple–test method and compare its performance with the box–and–whisker plot method used by the original authors. The individual data for six selected compounds (phenan–threne, chrysene, fluorenthene, pyrene, benz(a) anthracene, and benz(a) pyrene) were summarized in our earlier paper (see table 9 in Verma and Quiroz–Ruiz, 2006, compiled from the original report by Villeneuve etal, 2002). Our multiple–test method consists of applying all nine single–outlier (with 13 test variants) and seven multiple–outlier tests (with 20 test variants) to a given set of data (see Table 2). Note one test (N4) is common to both these categories; in fact, we have used 15 (and not 16) tests –Nl to N15 (because precise critical values fortest N16 are still not available; seeBarnett and Lewis, 1994, or Verma, 2005). The performance of these tests for detecting discordant outliers in each set of petroleum hydrocarbon data is summarized in Table 2, in which all applied tests, along with the tests that were successful or unsuccessful in detecting outliers, in the categories of single– and multiple–outlier tests are listed.
After the identification of discordant outliers, these were eliminated and the tests applied to the remaining data until no more outliers were detected by any of the 15 tests or 33 test variants. The concentration data along with the basic statistical information are summarized in Table 3. It is not surprising to see such highly dispersed data for a given compound in the same sample distributed and analyzed by laboratories around the world (see the initial range of individual values that differ by nearly two orders of magnitude); unfortunately, this is the "state–of–the–art" in geochemistry! The same type of situation should exist in other science or engineering fields as well (see for example, the numerous references cited above for "Quality Assurance and Assessment Programs").
More discordant outliers were detected by the present multiple–test method than the box–and–whisker plot method used by the original authors (Villeneuve et al., 2002) in the data for most compounds listed in Table 3. Note the initial mean and standard deviation data strongly differ from the final statistical parameters.
We conclude that the multiple–test method exemplified in this work can be advantageously used in future to arrive at the final statistical parameters in such inter–laboratory studies. This multiple–test method was already proposed and documented by Verma and collaborators (Verma, 1997, 1998,2005; Verma et al, 1998; Guevara et al, 2001; Velasco et al, 2000; Velasco–Tapia et al, 2001). The availability of new, precise and accurate critical values for sample sizes up to 100 (this work; and Verma and Quiroz–Ruiz, 2006) makes this proposal much more powerful than the other methods such as the box–and–whisker plot method.
Example 2: Two chemical elements in a geochemical reference material from Japan
We present the example of just two elements (a major element or oxide MgO and a trace element Zr) in a rock reference material peridotite JP–1 from Japan. The same kind of reasoning will be valid for other elements in JP–1 and for all other international geochemical reference materials. The individual data were downloaded from the Geological Survey of Japan–Geochemical Reference Samples Database (GSJ–GRS, 2006) and are presented in the footnote of Table 2. The results of the application of our multiple–test method are summarized in Tables 2 and 3. Unfortunately, no information is available on the currently used method of data processing for the Japanese geochemical reference materials; the only available information was taken from Imai et al. (1995). These authors had used the two standard deviation method for outlier detection, which was already criticized by Verma and collaborators (Verma, 1997, 1998, 2005; Verma et al, 1998; Guevara et al, 2001; Velasco et al, 2000; Velasco–Tapia et al, 2001).
Example 3: The need of outlier tests in other geoscience studies
We now briefly comment on the need of using the above multiple–test method in numerous geoscience studies. As the third example, we applied the multiple–test method to the oxygen isotope data for the Los Azufres hydrothermal system (see individual data in the 4th column of table 3 of Torres–Alvarado, 2002) to test if there were any outliers in these data. Our application of the multiple–test method showed no outliers in this dataset, implying that the conventional location and scale parameters –mean and standard deviation– can be safely used to handle these data (see Verma, 2005 for more details).
This and the other two examples (Tables 2 and 3) clearly show the need for processing the raw univariate data by the multiple–test method, irrespective of if or not any outliers were eventually detected. This is true, for example, for the recent studies by Mendoza–Amézquita et al. (2006) and Ramos–Arroyo and Siebe–Grabach (2006). These authors did not actually report the individual data; consequently, the multiple–test method could not be applied by us. However, they reported mean and standard deviation values as indicators of central tendency (location) and dispersion (scale) parameters, for which it is always advisable to first apply our multiple–test method to identify any discordant outliers and only then use these location and scale parameters for interpretation purposes (see Verma, 2005 for more details). The discordant outliers, if present, are of much value to further understand the geological processes (again, see Verma, 2005 for more details).
As yet other application examples, we may mention the chemical data for a given mineral or rock type such as those presented by Vattuone et al. (2005), Rodriguez (2005), or Lozano and Bernal (2005). We suggest that these raw data should first be processed using this outlier–scheme (multiple–test method) and only then their mean and standard deviation can be used as the proper central tendency and dispersion parameters for a given mineral or rock type.
Finally, as an example, we may mention that the application of our multiple–test method may also be highly advantageous for correctly processing the grain size data of sands recently reported by Kasper–Zubillaga and Carranza–Edwards (2005), in which the mean, skewness andkurtosis parameters were used (after applying some other tests) for interpreting these data. These authors used a probably inappropriate Kolmogorov–Smirnov one–sample test for normality, which is best applied when the mean and standard deviation of the normal distribution are known a priori and not estimated from the data (Statistica for Windows, 1998). The Levene's test used by these authors has also certain restrictions and conditions to be fulfilled.
In summary, therefore, the multiple–test method proposed and exemplified in our paper is strongly recommended to be used for experimental data under the assumption that the data are drawn from a normal distribution and departure from this assumption due to any contamination or presence of discordant outliers can be properly handled by tests Nl to N15 (15 tests with their 33 variants). Unfortunately, most commercially available software packages do not pay due attention to these fundamental tests. Nevertheless, the computer program currently under preparation by our group will greatly facilitate the use of our multiple–test method. In the mean while, the interested persons can use the Statistica spreadsheet prepared by us or an old computer program SIP VADE (Verma et al., 1998) to process their experimental data.
Two standard deviation method
Comparison with a valid multiple–outlier test
We present additional arguments against the use of the "two standard deviation" method (henceforth called the 2s method) by comparing the performance of this method with that of just one multiple–outlier test N3–k=2,3,4 (with three variants). For this purpose, we applied this test to the inter–laboratory data on the geochemical reference material granodiorite GSP–1 from U.S.A., compiled and processed by Gladney et al. (1992) using the 2s method. In order to make this comparison objective, test N3–k=2,3,4 was applied at the 95% confidence level (or 5% significance level) to exactly the same compiled data that had been evaluated by Gladney et al. (1992).
The results obtained for the trace element data with initial number of observations between 20 and 100, are shown in Table 4. The inter–laboratory data show a large scatter for most elements as seen from the wide range of values as well as from large standard deviation values. Test N3–k=2,3,4 detected, in general, more discordant outlier than the 2s method (Table 4). Agraphical comparison of the results is presented in Figure 4. Those data that fall close to the diagonal line in Figures 4a and 4b or close to the horizontal "zero value" line in Figures 4c and 4d show no significant differences between the two methods. However, many elements plot away from these reference lines, and document the superiority of test N3–k=2,3,4 as compared to the 2s method (Figure 4).
It is beyond any reasonable doubt that the combined performance of all the tests proposed in our multiple–test method should be at least similar to, if not better than, the test N3–k=2,3,4 evaluated here. Therefore, the 2s method can be safely abandoned, and our proposal of multiple–test method adopted for all future work, especially for evaluating inter–laboratory compositional data.
Not recommended for samples of finite size
We present more arguments against the use of the 2s method to process inter–laboratory compositional data (or for that matter, any other kind of univariate data). We have plotted in Figure 5 the 95% and 99% critical values for tests Nl and N2. The use of the 2s method is shown schematically as the solid horizontal line, which means that all individual data falling anywhere below this line (in the field marked A) will be considered as legitimate or valid observations, whereas any observations lying above this line in any of the fields B, C, or D will be considered discordant outliers. Note the sample size–independent nature of the 2s method represented schematically by the "critical values" lying on the horizontal line in Figure 5 –an erroneous property according to Barnett and Lewis (1994). As was explained earlier, tests Nl and N2 are the statistically–correct versions of this 2s method; the corresponding critical values strongly depend on the sample size (see the different critical value "curves" –not "straight lines"– in Figure 5). The observations below a given curve, falling in both fields A and B for 95% CL, or in fields A, B, and C for 99% CL, will be considered as legitimate data, where as those falling above these curves (shown in blue for test Nl 95%CL, in red for test Nl 99%CL, in magenta for test N2 95%CL, and in green for test N2 99%CL) would be discordant outliers. Therefore, in most cases, legitimate observations (those falling in fields B or C) will be erroneously eliminated by the 2s method, whereas some (those falling in field E) will be erroneously retained by the 2s method. This reasoning combined with the problems mentioned earlier, clearly show that the 2s method should be abandoned in future for data handling of samples of finite sizes such as those encountered in most experimental work, including the study of international geochemical reference materials. Instead, our present multiple–test method should be adopted for these purposes.
CONCLUSIONS
We have used our established and well–tested Monte Carlo type simulation procedure for generating new, precise and accurate critical values for nine discordancy tests with 22 test variants for sample sizes up to 100. Occasionally, these values were found to be similar to (differences <0.4%), but more precise and accurate than the existing literature values; for most tests, however, larger differences (˜0.4–20%) were observed between the two sets.
These new critical values will be of great use in many diverse fields of science and engineering. Three specific examples are presented to highlight the use of these new critical values as well as those recently published by Verma and Quiroz–Ruiz (2006).
The multiple–test method outlined in the present work seems to perform better than the box–and–whisker plot method used for processing inter–laboratory data on petroleum hydrocarbon compounds.
Finally, the frequently used "two standard deviation" (2s) method is shown to be statistically erroneous and less efficient in detection of outliers in comparison to our proposed multiple–test method, and should, therefore, be abandoned. The multiple–test method (15 tests with 33 variants) is shown to be highly suited for handling of experimental data, including those for international geochemical reference materials.
ACKNOWLEDGEMENTS
This research was partly supported by the Sistema Nacional de Investigadores (Mexico), through a scholarship to A. Quiroz–Ruiz as the first author's (SPV) "Ayudantes de Investigador Nacional Nivel 3". The revision of this manuscript benefited from constructive comments from two anonymous reviewers.
REFERENCES
Alberdi, M.T., Corona–M., E., 2005, Revisión de los gonfoterios en el Cenozoico tardío de México: Revista Mexicana de Ciencias Geológicas, 22(2), 246–260. [ Links ]
Ando, A., Mita, N., Terashima, S., 1987, 1986 values for fifteen GSJ rock reference samples, "Igneous rock series": Geostandards Newsletter, 11(1), 159–166. [ Links ]
Ando, A., Kamioka, H., Terashima, S., Itoh, S., 1989, 1988 values for GSJ rock reference samples, " Igneous rock series": Geochemical Journal, 23, 159–166. [ Links ]
Barnett, V., Lewis, 1, 1994, Outliers in Statistical Data: Chichester, John Wiley, Third edition, 584 p. [ Links ]
Bartlett, J.M., Dougherty–Page, J.S., Harris, N.B.W., Hawkesworth, C.J., Santosh, M., 1998, The application of single zircon evaporation and model Nd ages to the interpretation of polymetamorphic terrains: an example from the Proterozoic mobile belt of south India: Contributions to Mineralogy and Petrology, 131(2–3), 181–195. [ Links ]
Batjes, N.H., 2005, Organic carbon stocks in the soils of Brazil: Soil Use and Management, 21(1), 22–24. [ Links ]
Bendre, S.M., Kale, B.K., 1987, Masking effect for outliers in normal samples: Biometrika, 74(4), 891–896. [ Links ]
Buckley, J.A., Georgianna, T.D., 2001, Analysis of statistical outliers with application to whole effluent toxicity testing: Water Environment Research, 73(5), 575–583. [ Links ]
Cooper S.J., Trinklein N.D., Anton E.D., Nguyen L., Myres R.M., 2006, Comprehensive analysis of transcriptional promoter structure and function in 1% of the human genome: Genome Research 16(1), 1–10. [ Links ]
Dávalos–Álvarez, O.G., Nieto–Samaniego, A.F., Alaniz–Alvarez, S.A., Gómez–González, J.M., 2005, Las fases de deformación cenozoica en la región de Huimilpan, Querétaro, y su relación con la sismicidad local: Revista Mexicana de Ciencias Geológicas, 22(2), 129–147. [ Links ]
David, H.A., Paulson, A.S., 1965, The performance of several tests for outliers: Biometrika, 52, 429–436. [ Links ]
Dixon, W.J., 1950, Analysis of extreme values: Annals of Mathematical Statistics, 21(4), 488–506. [ Links ]
Dixon, W. J., 1951, Ratios involving extreme values: Annals of Mathematical Statistics, 22(1), 68–78. [ Links ]
Dixon, W.J., 1953, Processing data for outliers: Biometrics, 9(1), 74–89. [ Links ]
Dougherty–Page, J.S., Bartlett, J.M., 1999, New analytical procedures to increase the resolution of zircon geochronology by the evaporation technique: Chemical Geology, 153(1–4), 227–240. [ Links ]
Dybczyñski, R., 1980, Comparison of the effectiveness of various procedures for the rejection of outlying results and assigning consensus values in interlaboratory programs involving determination of trace elements o rradionuclides: Analytica Chimica Acta, 117(1), 53–70. [ Links ]
Dybczyñski, R., Tugsavul, A., Suschny, O., 1979, Soil–5, a new IAEA certified reference material for trace element determinations: Geostandards Newsletter, 3(1), 61–87. [ Links ]
Dybczyñski, R., Polkowska–Motrenko, H., Samczynski, Z., Szopa, Z., 1998, Virginia tobacco leaves (CTA–VTL–2) – new Polish CRM for inorganic trace analysis including microanalysis: Fresenius Journal of Analytical Chemistry, 360(3–4), 384–387. [ Links ]
Esquivel–Macías C, León–Olvera, R.G., Flores–Castro, K., 2005, Caracterización de una nueva localidad fosilífera del Jurásico Inferior con crinoides y amonites en el centro–oriente de México: Revista Mexicana de Ciencias Geológicas, 22(1), 97–114. [ Links ]
ESMP, 2006, Detection and Accommodation of Outliers in Normally Distributed Data Sets (online) by Fallón A., Spada, C: Environmental Sampling and Monitoring Primer, http://ewr.cee.vt.edu/environmental/teach/smprimer/outlier/outlier.html. [ Links ]
Freeman, B. D., Quezado, Z., Zeni, F., Natanson, C, Danner, R.L., Banks, S., Quezado, M., Fitz, Y., Bacher, J., Eichacker, P.Q., 1997, rG–CSF reduces endotoxemia and improves survival during E–coli pneumonia: Journal of Applied Physiology, 83(5), 1467–1475. [ Links ]
Gill, U., Covaci, A., Ryan, J.J., Emond, A., 2004, Determination of persistent organohelogenated pollutants in human hair reference material (BCR 397); an interlaboratory study: Analytical and Bioanalytical Chemistry, 380(7–8), 924–929. [ Links ]
Gladney, E.S., Roelandts, I., 1988, 1987 compilation of elemental concentration data for USGS BIR–1, DNC–1 and W–2: Geostandards Newsletter, 12(1), 63–118. [ Links ]
Gladney, E.S., Roelandts, I., 1990, 1988 compilation of elemental concentration data for USGS geochemical exploration reference materials GXR–1 to GXR–6: Geostandards Newsletter, 14(1), 21–118. [ Links ]
Gladney, E.S., Jones, E.A., Nickell, E.J., 1992, 1988 compilation of elemental concentration data for USGS AGV–1, GSP–1 and G–2: Geostandards Newsletter, 16(2), 111–300. [ Links ]
Gladney, E.S., Jones, E.A., Nickell, E.J., Roelandts, I., 1991, 1988 compilation of elemental concentration data for USGS DTS–1, G–l, PCC–1, and W–l: Geostandards Newsletter, 15(2), 199–396. [ Links ]
Graybeal, D.Y., DeGaetano, A.T., Eggleston, K.L., 2004, Improved quality assurance for historical hourly temperature and humidity; development and application to environmental analysis: Journal of Applied Meteorology, 43(11), 1722–1735. [ Links ]
Grubbs, F.E., 1950, Sample criteria for testing outlying observations: Annals of Mathematical Statistics, 21(1), 27–58. [ Links ]
Grubbs, F.E., 1969, Procedures for detecting outlying observations in samples: Technometrics, 11(1), 1–21. [ Links ]
Grubbs, F.E., Beck, G., 1972, Extension of sample sizes and percentage points for significance tests of outlying observations: Technometrics, 14(4), 847–854. [ Links ]
GSJ–GRS, 2006, GSJ Geochemical Reference samples DataBase (online): National Institute of Advanced Industial Science and Technology, Geochemical Standards Database, www.aist.go.jp/RIODB/geostand, accessed on April 6, 2006. [ Links ]
Guevara, M., Verma, S.P., Velasco–Tapia, F., 2001, Evaluation of GSJ intrusive rocks JG1, JG2, JG3, JG1a, and JGb1: Revista Mexicana de Ciencias Geológicas, 18(1), 74–88. [ Links ]
Guevara, M., Verma, S.P., Velasco–Tapia, F., Lozano–Santa Cruz, R., Girón, P., 2005, Comparison of linear regression models for quantitative geochemical analysis; Example of X–ray fluorescence spectrometry: Geostandards and Geoanalytical Research, 29(3), 271–284. [ Links ]
Hanson, D., Kotuby–Amacher, J., Miller, R.O., 1998, Soil analysis; Western States proficiency testing program for 1996: Fresenius Journal of Analytical Chemistry, 360(3–4), 348–350. [ Links ]
Harcourt, A.H., Coppeto, S.A., Parks, S.A., 2005, The distribution–abundance (density) relationship; its form and causes in a tropical mammal order, Primates: Journal of Biogeography, 32(4), 565–579. [ Links ]
Hawkins, D.M., 1979, Fractiles of an extended multiple outlier test: Journal of Statistical and Computational Simulations, 8, 227–236. [ Links ]
Hayes, K, Kinsella, T, 2003, Spurious and non–spurious power in performance criteria for tests of discordancy: Journal of the Royal Statistical Society, Series D (The Statistician), 52 (1), 69–82. [ Links ]
Hofer, J.D., Murphy, J.R., 2000, Structured use of the median in the analytical measurement process: Journal of Pharmaceutical and Biomedical Analysis, 23(4), 671–686. [ Links ]
Holcombe, G., Lawn, R., Sargent, M., 2004, Improvements in efficiency of production and traceability for certification of reference materials: Accreditation and Quality Assurance, 9(4–5), 198–204. [ Links ]
Ifrim, C, Stinnesbeck, W., Schafhauser, A., 2005, Maastrichtian shallow–water ammonites of northwestern Mexico: Revista Mexicana de Ciencias Geológicas, 22(1), 48–64. [ Links ]
Ihnat, M., 2000, Performance of NAA methods in an international interlaboratory reference material characterization campaign: Journal of Radioanalytical and Nuclear Chemistry, 245(1), 73–80. [ Links ]
Iglewicz, B., Martinez, J., 1982, Outlier detection using robust measures of scale: Journal of Statistical Computation and Simulation, 15, 285–293. [ Links ]
Imai, N., Terashima, S., Itoh, S., Ando, A., 1995, 1994 compilation of analytical data for minor and trace elements in seventeen GSJ geochemical reference samples, "Igneous rock series": Geostandards Newsletter, 19(2), 135–213. [ Links ]
Imai, N., H., S., Terashima, S., Itoh, S., Ando, A., 1996, 1996 Compilation of analytical data on nine GSJ geochemical reference samples, "sedimentary rock series": Geostandards Newsletter, 20 (2), 165–216. [ Links ]
In't Veld, PH., 1998, The use of reference materials in quality assurance programmes in food microbiology laboratories: International Journal of Food Microbiology, 45(1), 35–41. [ Links ]
Itoh, S., Terashima, S., Imai, N., Kamioka, H., Mita, N., Ando, A., 1993, 1992 compilation of analytical data for rare–earth elements, scandium, yttrium, zirconium and hafnium: Geostandards Newsletter, 17(1), 5–79. [ Links ]
Jakubowska, M., Kubiak, W.W., 2005, Removing spikes from voltammetric curves in the presence of random noise: Electroanalysis, 17(18), 1687–1694. [ Links ]
JGRMW, 2006, Japan Geochemical Reference Material Website, www.aist.go.jp/RIODB/Geostand/; accessed on April 6, 2006. [ Links ]
Kasper–Zubillaga, J.J., Carranza–Edwards, A., 2005, Grain size discrimination between sands of desert and coastal dunes from northwestern Mexico: Revista Mexicana de Ciencias Geológicas, 22(3), 383–390. [ Links ]
Kern, M., Preimesberger, T, Allesch, M., Pail, R., Bouman, J., Koop, R., 2005, Outlier detection algorithms and their performance in GOCE gravity field processing: Journal of Geodesy, 78(9), 509–519. [ Links ]
King, E.P, 1953, On some procedures for the rejection of suspected data: Journal of American Statistical Association, 48(263), 531–533. [ Links ]
Langton, S.D., Chevennement, R., Nagelkerke, N., Lombard, B., 2002, Analysing collaborative trials for qualitative microbiological methods; accordance and concordance: International Journal of Food Microbiology, 79(3), 175–181. [ Links ]
Lin, Z., Inn, K.G.W., Filliben, J.J., 2001, An alternative statistical approach for interlaboratory comparison data evaluation: Journal of Radioanalytical and Nuclear Chemistry, 248(1), 163–173. [ Links ]
Linkosalo, T, Hakkinen, R., Hari, P., 1996, Improving the reliability of a combined phenological time series by analyzing observation quality: Tree Physiology, 16(7), 661–664. [ Links ]
Lozano, R., Bernal, J.P., 2005, Assessment of eight new geochemical reference materials for XRF major and trace element analysis: Revista Mexicana de Ciencias Geológicas, 22(3), 329–344. [ Links ]
Luedeling, E., Nagieb, M., Wichern, F., Brandt, M., Deurer, M., Buerkert, A., 2005, Drainage, salt leaching and physico–chemical properties of irrigated man–made terrace soils in amountain oasis of northern Oman: Geoderma, 125(3–4), 273–285. [ Links ]
Lugo–Ospina, A., Dao, T.H., Van Kessel, J.A., Reeves III, J.B., 2005, Evaluation of quick tests for phosphorus determination in dairy manures: Environmental Pollution, 135(1), 155–162. [ Links ]
McMillan, R.G., 1971, Tests for one or two outliers in normal samples with unknown variance: Technometrics, 13, 87–100. [ Links ]
Mendoza–Amézquita, E., Armienta–Hernández, M.A., Ayora, C, Soler, A., Ramos–Ramírez, E., 2006, Potencial lixiviación de elementos traza en jales de las minas La Asunción y Las Torres, en el Distrito Minero de Guanajuato, México: Revista Mexicana de Ciencias Geológicas, 23(1), 75–83. [ Links ]
Morabito, R., Massanisso, P, Cámara, C, Larsson, T, Freeh, W., Kramer, K.J.M., Bianchi, M., Muntau, H., Donard, O.F.X., Lobinski, R., McSheehy, S., Pannier, F., Potin–Gautier, M., Gawlik, B.M., Bowadt, S., Quevauviller, P, 2004, Towards anew certified reference material for butyltins, methylmercury and arsenobetaine in oyster tissue: Trends in Analytical Chemistry, 23(9), 664–676. [ Links ]
Moran, M.A., McMillan, R.G., 1973, Tests for one or two outliers in normal samples with unknown variance; a correction: Technometrics, 15(3), 637–640. [ Links ]
Morán–Zenteno, D.J., Alba–Aldave, L.A., Martinez–Serrano, R.G., Reyes–Salas, M.A., Corona–Esquivel, R., Angeles–García, S., 1998, Stratigraphy, geochemistry and tectonic significance of the Tertiary volcanic sequences of the Taxco–Quetzalapa region, southern Mexico: Revista Mexicana de Ciencias Geológicas, 15(2), 167–180. [ Links ]
Otto, M., 1999, Chemometrics. Statistics and Computer Application in Analytical Chemistry: Weinheim, Wiley–VCH, 314 p. [ Links ]
Patriarca, M., Chiodo, E, Castelli, M., Corsetti, E, Menditto, A., 2005, Twenty years of the Me.Tos. project; an Italian national external quality assessment scheme for trace elements in biological fluids: Microchemical Journal, 79(1–2), 337–340. [ Links ]
Pearson, E.S., Hartley, H.O., 1976, Biometrika Tables for Statisticians, v. I: England, Biometrika Trust, third edition, 263 p. [ Links ]
Prescott, P., 1978, Examination of the behaviour of tests for outliers when more than one outlier is present: Applied Statistics, 27(1), 10–25. [ Links ]
Prescott, P., 1979, Critical values for a sequential test for many outliers: Applied Statistics, 28(1), 36–39. [ Links ]
Quesenberry, C.P., David, H. A., 1961, Some tests for outliers: Biometrika, 48, 379–387. [ Links ]
Ramos–Arroyo, Y.R., Siebe–Grabach, CD., 2006, Estrategia para identificar jales con potencial de riesgo ambiental en un distrito minero; estudio de caso en el Distrito de Guanajuato, Mexico: Revista Mexicana de Ciencias Geológicas, 23(1), 54–74. [ Links ]
Reed, D.S., Smoll, I, Gibbs, P., Little, S.F., 2002, Mapping of antibody responses to the protective antigen of Bacillus anthracis by flow cytometric analysis: Cytometry, 49(1), 1–7. [ Links ]
Rodríguez, S.R., 2005, Geology of Las Cumbres volcanic complex, Puebla and Veracruz states, México: Revista Mexicana de Ciencias Geológicas, 22(2), 181–198. [ Links ]
Rosner, B., 1975, On the detection of many outliers: Technometrics, 17, 221–227. [ Links ]
Santoyo, E., Guevara, M., Verma, S.P, 2006, Determination of lanthanides in international geochemical reference materials by reversed– phase high performance liquid chromatography; An application of error propagation theory to estimate total analysis uncertainties: Journal of Chromatography A, 1118(1), 73–81. [ Links ]
Schaber, J., Badeck, F. W., 2002, Evaluation of methods for the combination of phenological time series and outlier detection: Tree Physiology, 22(14), 973–982. [ Links ]
SCNPHT, 2006, Statistics for Chemists, (Non–parametric Hypothesis Tests) (online): http://www.webchem.science.ru.nl/cgi–bin/Stat/HypT/nphypt.pl. [ Links ]
Sevransky, J., Vandivier, R.W., Gerstenberger, E., Correa, R., Ferantz, V, Banks, S.M., Danner, R.L., Eichacker, P.Q., Natanson, C, 2005, Prophylactic high–dose Nω–monomethyl–L–arginine prevents the late cardiac dysfunction associated with lethal tumor necrosis factor–a challenge in dogs: Shock, 23(3), 281–288. [ Links ]
Shapiro, S.S., Wilk, M.B.,Chen, H.J., 1968, A compartive study of various tests for normality: Journal of American Statistical Association, 63, 1343–1371. [ Links ]
Shoemaker, D.P, Garland, C.W., Nibler, J.W., 1996, Experiments in Physical Chemistry. Sixth edition: New York, McGraw Hill, 778 p. [ Links ]
Sieber, J., Broton, D., Fales, C, Leigh, S., MacDonald, B., Marlow, A., Nettles, S., Yen, J., 2002, Standards reference materials for cements: Cement and Concrete Research, 32(12), 1899–1906. [ Links ]
Srivastava, M.S., 1980, Effect of equicorrelation in detecting a spurious observation: Canadian Journal of Statistics, 8(2), 249–251. [ Links ]
Stancak, A., Hoechstetter, K., Tintera, J., Vrana, J., Rachmanova, R., Kralik, J., Scherg, M., 2002, Source activity in the human secondary somatosensory cortex depends on the size of corpus callosum: Brain Research, 936(1–2), 47–57. [ Links ]
Statistica for Windows, 1998, General Convention and Statistics I. Second edition: Tulsa, OK, Statsoft, 1878 p. [ Links ]
Stefansky, W., 1971, Rejecting outliers by maximum normed residual: Annals of Mathematical Statistics, 42(1), 35–45. [ Links ]
Stevens, R.J., O'Bric, C.J., Carton, O.T., 1995, Estimating nutrient content of animal slurries using electrical conductivity: Journal of Agricultural Science, 125(2), 233–238. [ Links ]
Stoch, H., Steele, T.W., 1978, Analyses, by several laboratories, of three ferromanganese slags: Network of Independent Monitors (NIM) South Africa Report 1965, 34 p. [ Links ]
Suhren G., Walte H.G., 2001, Determination of precision data of the bactoscan FC–method by an interlaboratory study: Kieler Milchwirtschaftliche Forschungsberichte 53(4): 269–282. [ Links ]
Taylor, B.J., 2000, A statistical analysis of the metallicities of nine old superclusters and moving groups: Astronomy and Astrophysics, 362, 563–579. [ Links ]
Thomulka, K.W., Lange, J.H., 1996, Amixture toxicity study employing combinations of tributyltin chloride, dibytyltin dichloride, and tin chloride using the marine bacterium vibrio harveyi as the test organism: Ecotoxicology and Environmental Safety, 34(1), 76–84. [ Links ]
Tietjen, G.L., Moore, R.H., 1972, Some Grubbs–type statistics for the detection of several outliers: Technometrics, 14(3), 583–597. [ Links ]
Tietjen, G.L., Moore, R.H., 1979, Corrigendum "Some Grubbs–type statistics for the detection of several outliers": Technometrics, 21(3), 396. [ Links ]
Tigges, M., Iuvone, P.M., Fernández, A., Sugrue, M.F., Mallorga, P.J., Laties, A.M., Stone, R.A., 1999, Effects of muscarinic cholinergic receptor antagonists on postnatal eye growth of rhesus monkeys: Optometry and Vision Science, 76(6), 397–407. [ Links ]
Tiku, M.L., 1975, A new statistic for testing suspected outliers: Communications in Statistics, 4(8), 737–752. [ Links ]
Tiku, M.L., 1977, Rejoinder; Comment on 'Anew statistic for testing suspected outliers': Communications in Statististics, Theory and Methods, A6( 14), 1417–1422. [ Links ]
Torres–Alvarado, I.S., 2002, Chemical equilibrium in hydrothermal systems; the case of Los Azufres geothermal field, Mexico: International Geology Review, 44(7), 639–652. [ Links ]
Treviño–Cázares, A., Ramírez–Fernández, J.A., Velasco–Tapia, F., Rodriguez–Saavedra, P., 2005, Mantle xenoliths and their host magmas in the Eastern Alkaline Province (NE Mexico): International Geology Review, 47(12), 1260–1286. [ Links ]
Vattuone, M.E., Latorre, CO., Leal, PR., 2005, Polimetamorfismo de muy bajo a bajo grado en rocas volcánicas jurásico–cretácicas al sur de Cholila, Chubut, Patagonia Argentina: Revista Mexicana de Ciencias Geológicas, 22(3), 315–328. [ Links ]
Velasco, F., Verma, S.P, Guevara, M., 2000, Comparison of the performance of fourteen statistical tests for detection of outlying values in geochemical reference material databases: Mathematical Geology, 32(4), 439–464. [ Links ]
Velasco–Tapia, F., Guevara, M., Verma, S.P, 2001, Evaluation of concentration data in geochemical reference materials: Chemie der Erde, 61(1), 69–91. [ Links ]
Verma, S.P, 1997, Sixteen statistical tests for outlier detection and rejection in evaluation of International Geochemical Reference Materials; example of microgabbro PM–S: Geostandards Newsletter, Journal of Geostandards and Geoanalysis, 21(1), 59–75. [ Links ]
Verma, S.P, 1998, Improved concentration data in two international geochemical reference materials, USGS basalt BIR–1 and GSJ peridotite JP–1) by outlier rejection: Geofísica Internacional, 37(3), 215–250. [ Links ]
Verma, S.P, 2005, Estadística Básica para el Manejo de Datos Experimentales; Aplicación en la Geoquímica (Geoquimiometría): México, D.F., Universidad Nacional Autónoma de México, 186 p. [ Links ]
Verma, S.P, 2006, Extension–related origin of magmas from a garnet–bearing source in the Los Tuxtlas volcanic field, Mexico: International Journal of Earth Sciences (Geologische Rundschau), 95(5), 871–901. [ Links ]
Verma, S.P, Quiroz–Ruiz, A., 2006, Critical values for six Dixon tests for outliers in normal samples up to sizes 100, and applications in science and engineering: Revista Mexicana de Ciencias Geológicas, 23(2), 133–161. [ Links ]
Verma, S.P, Orduña–Galván, L.J., Guevara, M., 1998, SIPVADE; Anew computer programme with seventeen statistical tests for outlier detection in evaluation of international geochemical reference materials and its application to Whin Sill dolerite WS–E from England and Soil–5 from Peru: Geostandards Newsletter, Journal of Geostandards and Geoanalysis, 22(2), 209–234. [ Links ]
Verma, S.P, Pandarinath, K., Santoyo, E., González–Partida, E., Torres–Alvarado, I.S., Tello, E., 2006, Fluid chemistry and temperatures prior to exploitation at the Las Tres Vírgenes geothermal field, Mexico: Geothermics, 35(2), 156–180. [ Links ]
Villaseñor, A.B., González–León, CM., Lawton, TE, Aberhan, M., 2005, Upper Jurassic ammonites and bivalves from Cucurpe Formation, Sonora (Mexico): Revista Mexicana de Ciencias Geológicas, 22(1), 65–87. [ Links ]
Villeneuve, J.–P., de Mora, S.J., Cattini, C, 2002, World–wide and regional intercomparison for the determination of organochlorine compounds and petroleum hydrocarbons in sediment sample IAEA–417: Vienna, Austria, International Atomic Energy Agency, Analytical Quality Control Services, 136 p. [ Links ]
Villeneuve, J.–P., de Mora, S., Cattini, C, 2004, Determination of organo–chlorinated compounds and petroleum in fish–homogenate sample IAEA–406; results from a worldwide interlaboratory study: Trends in Analytical Chemistry, 23(7), 501–510. [ Links ]
Wang, X.–D., Soderlund, U., Lindh, A., Johansson, L., 1998, U–Pb and Sm–Nd dating of high–pressure granulite– and upper amphibolite facies rocks from SW Sweden: Precambrian Research, 92(4), 319–339. [ Links ]
Woitge, H.W., Scheidt–Nave, C, Kissling, C. Leidig–Bruckner, G., Meyer, K., Grauer, A., Scharla, S.H., Ziegler, R., Seibel, M.J., 1998, Seasonal variation of biochemical indexes of bone turnover; Results of a population–based study: Journal of Clinical and Endocrinological Metabolism, 83(1), 68–75. [ Links ]
WORM Database, 2006, http://www.wormbase.org/ [ Links ]
Yurewicz, K.L., 2004, A growth/mortality trade–off in larval salamanders and the coexistence of intraguild predators and prey: Oecologia, 138(1), 102–111. [ Links ]
Zaric S., Niketic S.R., 1997, The anisotropic n–effect of the nitro group in ammine–nitro cobalt(III) complexes: Polyhedron, 16(20), 3565–3569. [ Links ]
Zhang, J, 1998, Tests for multiple upper or lower outliers in an exponential sample: Journal of Applied Statistics, 25(2), 245–255. [ Links ]
Zhang, J, Wang, X., 1998, Unmasking test for multiple upper or lower outliers in normal samples: Journal of Applied Statistics, 25(2), 257–261. [ Links ]














