Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agricultura técnica en México
versión impresa ISSN 0568-2517
Agric. Téc. Méx vol.32 no.2 México may./ago. 2006
Artículos
Escurrimiento superficial como fuente de excesos de agua sobre terrenos agrícolas tropicales*
Surface runoff as a source of excess water on tropical farmlands
Pablo Miguel Coras Merino1, , Federico Hahn Schlam1, Lamine Diakite Diakite1 y Ramón Arteaga Ramírez1
, Federico Hahn Schlam1, Lamine Diakite Diakite1 y Ramón Arteaga Ramírez1
1 Departamento de Irrigación, Universidad Autónoma Chapingo. Km 38.5 carretera México–Texcoco. 56230 Chapingo, Estado de México, México.
 Autor para correspondencia:
Autor para correspondencia:
e–mail: mpcoras@correo.chapingo.mx
* Recibido: Mayo de 2005
Aceptado: Mayo de 2006
RESUMEN
El municipio de Huimanguillo, en el estado de Tabasco, México, es afectado por el anegamiento de las aguas de escurrimiento sobre la superficie de terrenos agrícolas, perdiéndose total o parcialmente la producción de los cultivos. Con la finalidad de analizar este problema se plantearon los siguientes objetivos: calcular el escurrimiento superficial originado por lluvias máximas consecutivas a través de cinco métodos y estimar, con el mejor método identificado, los gastos hidráulicos por hectárea a remover por drenes colectores. El estudio se realizó en el año 2003. Se definieron las lluvias de diseño para los cultivos chile, frijol, sorgo y pasto, y se calculó el escurrimiento real en 24 h, así como la descarga de diseño para definir el sistema de drenaje en cada cultivo. Se encontró que los escurrimientos superficiales en 24 h y las descargas de diseño estimadas variaron entre métodos y cultivos. Se aceptó el método del Número de la Curva para estimar las lluvias de diseño y descargas a remover por considerar las variables edáficas, climáticas, hidrológicas y agronómicas sencillas de aplicar. Los valores de escurrimiento superficial y descarga de diseño obtenidos fueron: 42.00 mm y 0.55 m3 s–1 para el cultivo de chile; 148.88 mm y 2.12 m3 s–1 para frijol; 130.84 mm y 1.15 m3 s–1 para sorgo y 79.37 mm y 0.89 m3 s–1 para pasto.
Palabras clave: Precipitación, drenaje agrícola.
ABSTRACT
The Huimanguillo county in the state of Tabasco, Mexico, is affected by flooding that results from heavy water surface runoff that is deposited on farmland, therefore crop production is frequently lost. In order to analyze this problem the following objectives were stated: determine surface runoff due to maximum consecutive rains throughout five methods and estimate, with the best method identified, the discharge of water per hectare to be removed by drain collectors. The study was conducted in 2003. Design rainfalls were defined for chili pepper, common bean, sorghum, and grass, the real runoff in 24 h and the design discharge were also calculated to define the drainage system suited for each crop. It was found that the surface runoff in 24 h and the estimated design discharges varied with the utilized method and crop. The Curve Number method was chosen because it takes into consideration information on simple and easy to use variables of soil, climate, and hydrological and agronomic factors. Run off and discharge values of 42.00 mm and 0.55 m3 s–1 were defined for chili pepper, 148.88 mm and 2.12 m3 s–1 for common bean, 130.84 mm and 1.15 m3 s–1 for sorghum, and 79.37 mm and 0.89 m3 s–1 for grass, respectively.
Key words: Rainfall, farmland drainage.
INTRODUCCIÓN
La necesidad de aumentar las áreas de cultivo debido a la constante demanda de alimentos, mantiene a los investigadores en una intensa búsqueda de medidas que permitan el mejor aprovechamiento de los recursos agua y suelo en áreas tropicales húmedas; a pesar de las limitantes que tienen para su aprovechamiento agrícola por la falta de información edáfica, agronómica e hidrológica, éstas representan una reserva importante para la producción de alimentos para el país.
Las condiciones de exceso de agua sobre la superficie del suelo en el trópico húmedo se presentan en áreas planas y bajas con relación a áreas circundantes, en donde no existe una salida de agua por gravedad, razón por la cual el hombre ha tenido que hacer uso de artificios o técnicas que le permiten aprovechar estas áreas inundables.
La protección de las tierras agrícolas ante inundaciones es prioridad en países con altas precipitaciones pluviales de origen ciclónico en verano. El desarrollo de métodos para el diseño de estructuras de protección es por lo tanto una línea de investigación prioritaria (Carrillo et al., 2001).Una solución es el drenaje agrícola, el cual, según Rojas (1976) y Martínez (1986) consiste en la eliminación, por medios artificiales, del exceso de agua en el suelo o de la superficie del terreno, siendo su objetivo hacer al suelo más apto para la agricultura a fin de aumentar la producción y maximizar su beneficio neto.
La necesidad del drenaje superficial se justifica en zonas donde los factores climáticos, hidrológicos, edáficos, topográficos y de uso de la tierra, dan lugar a que el agua inunde la superficie del suelo, durante un tiempo superior al que los cultivos pueden soportar sin manifestar efectos significativos sobre los rendimientos (Herrera et al., 1999).
El exceso de agua sobre los terrenos tiene cuatro causas principales: precipitación, inundaciones, limitaciones topográficas y edáficas. La precipitación es la principal fuente de exceso de agua; las inundaciones son consecuencia de la precipitación y las limitaciones topográficas y edáficas que agravan la acción de las causas anteriores (Rojas, 2002).
Kraijenhoff y Van De Seur (1977) mencionan que entre los factores que afectan los escurrimientos se encuentran los siguientes: precipitación (intensidad, duración y área de distribución, y frecuencia); fisiográfico (área de la cuenca, topografía, forma de la cuenca, red de drenaje, pendiente y longitud del cauce); físico (cubierta del suelo, filtraciones superficiales y tipo de suelo).
Dentro del campo de la hidrología el escurrimiento es uno de los factores que más influyen en los proyectos agrícolas. En el sureste del país se tiene clima tropical, el cual se caracteriza por lluvias intensas de corta duración, que en muchos casos superan la capacidad de infiltración del suelo, provocando que el agua corra por la superficie o se encharque.
El escurrimiento con frecuencia se expresa como altura de lámina de agua y en el caso de terrenos inundables constituye la cantidad de agua que se requiere sacar del área de drenaje en un período de tiempo determinado. Esta lámina de agua se conoce como el coeficiente de drenaje y puede variar para un tiempo de 24 h, de 0.6 a 10.16 mm; con mayor frecuencia varía de 0.95 a 5 mm (Luthin, 1977). El cálculo del coeficiente de drenaje es una de las partes importantes en el diseño de los sistemas de drenaje en cuencas pequeñas; los resultados que se obtienen se usan para dimensionar los canales de desagüe y las obras hidroagrícolas. Un error en el cálculo trae consigo un sobredimensionamiento del sistema y por tanto incrementa el costo de la obra, o bien, un subdimensionamiento y por tanto pérdidas en los beneficios esperados.
La capacidad de una zanja abierta debe ser adecuada para eliminar el agua superficial y subsuperficial a una velocidad que no cause daños a los cultivos. Las zanjas abiertas normalmente no se diseñan para llevar un escurrimiento máximo, debido a que se requiere levantar secciones transversales grandes con pendientes planas y económicamente no sería factible su construcción.
En Estados Unidos se obtuvieron, por medio de aforos, los gastos unitarios de lluvias en exceso en cuencas planas (pendiente de 1% o menores), encontrándose que el gasto disminuye a medida que aumenta el área de aportación al dren, relación que fue establecida mediante ecuaciones que estiman los gastos de diseño de los drenes (Martínez, 1986; SCS, 1972).
Para las condiciones climáticas de Cuba, Monteagudo (1981) desarrolló un algoritmo matemático que permite determinar la precipitación para una probabilidad dada a partir del mapa isoyético al 1% de probabilidad; la precipitación así estimada fue utilizada en el Método Racional Modificado por éste autor, para estimar la descarga de diseño.
El intervalo entre cada ocasión en que hay escurrimiento, o bien un determinado valor de ese escurrimiento para una serie dada de condiciones y las necesidades de drenaje del cultivo, son esenciales para hacer un diseño apropiado de los drenes. Generalmente se pueden conseguir los datos de lluvia, tales como intensidad, duración, frecuencia y distribución superficial, y estacional (Luthin, 1977).
Para calcular el escurrimiento con datos de lluvia y de infiltración se necesita hacer la evaluación de las pérdidas sufridas por evaporación del agua superficial, transpiración, infiltración profunda, almacenamiento de agua en el perfil del suelo, que está influido por la humedad anterior y el almacenamiento superficial de tipo temporal y permanente.
Es sencillo estimar por métodos matemáticos o mecánicos, el volumen de escurrimiento en una cuenca agrícola cuando existe un cauce bien definido o un canal terminal con características físicas determinables. Sin embargo, no siempre es posible conducir el escurrimiento de una precipitación, en una cuenca dada, para poder medirlo directamente. Por ello, en muchos casos se tiene que recurrir a métodos empíricos de evaluación del escurrimiento (Kessler y Road, 1978; Pizarro, 1985; López, 1995; Becerra, 1999).
El estado de Tabasco, México, está localizado en una de las zonas agrícolas más afectadas por inundaciones perdiéndose total o parcialmente la producción de los cultivos. Con la finalidad del análisis y solución de este problema se plantearon los siguientes objetivos: a) Calcular el escurrimiento superficial originado por lluvias máximas consecutivas a través de cinco métodos, y b) Estimar, con el mejor método identificado, los gastos hidráulicos por hectárea a remover por los drenes colectores.
MATERIALES Y MÉTODOS
Caracterización del área de estudio
El estudio se realizó en el año 2003 en áreas agrícolas del municipio Huimanguillo, Tabasco, en 420 ha con problemas de inundación. Las características planimétricas y altimétricas se obtuvieron de la carta topográfica Huimanguillo E15C18 escala 1:50 000, elaborada por el INEGI (1999).
Las variables climáticas se obtuvieron de la base de datos ERICII (IMTA, 2000) estación meteorológica No. 27018 ubicada en los 17° 52' de latitud norte, 93° 28' de longitud oeste y altitud de 193 msnm. El clima se clasifica como cálido húmedo, lluvioso en verano y otoño. La lluvia promedio anual es de 1925 mm, existiendo dos períodos bien definidos, uno húmedo que ocurre desde el mes de junio hasta octubre donde cae 70% de la lluvia promedio anual (1357 mm) y otro seco desde el mes de noviembre hasta mayo con 30% (568 mm). La evaporación promedio anual es de 1515 mm (INEGI, 1999).
En la región agrícola se encuentran suelos de los tipos gleysol, vertisol, cambisol, fluvisol y los acrisol. En el área de estudio el suelo es vertisol con velocidad de infiltración básica de 3 mm h–1, determinada por pruebas de infiltración in situ y textura arcillosa del tipo montmorillonítico que dificultan el movimiento del agua en el perfil de suelo (Coras, 2000). El coeficiente de almacenamiento promedio en el suelo es de 68 mm (Coras, 2003). Las pendientes en el área de estudio son menores al 2%.
Procedimiento de cálculo
Definidos los tiempos de drenaje (td) para los cultivos chile, frijol, sorgo y pasto de acuerdo con FIRA (1985) y la curva de profundidad–duración para un período de retorno (tr) de 10 años, se determinaron las lluvias de diseño (LLd) procediendo a calcular los flujos superficiales a partir de los métodos siguientes:
Método del Balance Hídrico. Se basa en la ecuación simplificada del balance hídrico para estimar el escurrimiento en una cuenca agrícola (Rojas, 2002; Aparicio, 2004), siendo la misma:

donde:
E= Escurrimiento total durante el tiempo de drenaje (mmtd–1); P= Lluvia de diseño durante el tiempo de drenaje (mmtd–1); I= Infiltración total durante el tiempo de drenaje (mmtd–1) y Et= Evapotranspiración durante el tiempo de drenaje (mmtd–1).
Método del Número de la Curva (CN). Este método fue desarrollado por el Servicio de Conservación del Suelo de EE. UU. (SCS, 1972) para estimar el escurrimiento máximo en función de la precipitación y de las características físicas de la cuenca. El método se basa en la relación que existe entre la infiltración y el escurrimiento potencial y los valores reales de ambos. La relación es la siguiente:

donde:
F= Infiltración real (mm); S= Infiltración potencial (mm), E= Escurrimiento real (mm), Pe= Escurrimiento potencial o excesos de precipitación (mm).
El procedimiento de cálculo fue el siguiente:
• Determinar el área de la cuenca de drenaje, A.
• A partir del conocimiento de las características de la cuenca, se determina el grupo hidrológico a que pertenece y se obtiene el valor de CNII para las condiciones media de humedad antecedente.
• Con la precipitación acumulada de los cinco días antes del evento en consideración, se obtiene la categoría de humedad previa a la que pertenece.
• Con el valor de CNII y la categoría de humedad previa se determina el verdadero valor de CN.
• Se calcula la infiltración potencial (S) en mm y el escurrimiento real (E) en mm como:

donde:
P= Precipitación total estimada para el área en mm.
• El escurrimiento máximo se obtiene a partir del área de la cuenca, con las siguientes expresiones:
Cuencas >50 ha Q= CA5/6,
donde:

Cuencas >50 ha Q= cdA,
donde:

donde:
E= Escurrimiento en mm; C= Coeficiente de drenaje; (L s–1 ha–1); td= Tiempo de drenaje (h).
Q= Gasto (L s–1)
Método Racional Modificado. Es muy utilizado debido a su sencillez y puede ser expresado por:

donde:
Q= Escurrimiento máximo (m3 s–1); C= Coeficiente de escurrimiento; i= Máxima intensidad media de la lluvia crítica, para una duración de td, mm h–1; A= Área efectiva de la cuenca (ha).
El procedimiento a seguir fue el siguiente:
• Determinar el área de la cuenca.
• Estimar el coeficiente del drenaje (C) en función de la pendiente del terreno, vegetación y textura.
• En el caso de drenaje agrícola la duración del evento es igual al td.
• La intensidad para la lluvia de diseño se calcula con los métodos citados anteriormente.
• El escurrimiento máximo se calcula con la ecuación 7.
Fórmula de McMath. Esta fórmula es inducida a partir de transformaciones hechas al Método Racional Modificado (Batista, 1983). La descarga de diseño (Q) se estima a partir de:

donde:
Q= Escurrimiento máximo (m3 s–1); C= Coeficiente de escurrimiento de McMath tomado de Batista (1983); i= Intensidad de la lluvia (mm h–1), A= Área de la cuenca (ha), S= Pendiente máxima (mm–1).
El procedimiento de cálculo es similar al Método Racional Modificado, solo que el coeficiente de escurrimiento de McMath (C) se determina a partir de la suma de tres coeficientes relacionados con el tipo de vegetación, suelo y topografía.
Método de Boonstra. Según Boonstra (1989), seleccionada la curva de duración–profundidad– frecuencia, para obtener la descarga de diseño se procede de la siguiente forma:
• Se escoge la capacidad máxima de almacenamiento de agua en el suelo (mm) y se señala en el eje Y.
• A partir del valor de almacenamiento máximo del suelo se traza una recta tangente a la curva cuya frecuencia sea igual a la frecuencia de diseño.
• Se determina la pendiente de la recta trazada y el valor obtenido corresponde al hidromódulo de descarga en mm día–1.
• La descarga de diseño se obtiene a partir de la fórmula:

donde:
Q= Gasto de diseño (m3 s–1); q= Hidromódulo de descarga (mm d–1); A= Área de la cuenca (ha).
Dimensionamiento del dren colector
Los parámetros de dimensionamiento de una zanja de sección trapezoidal se indican en la Figura 1.
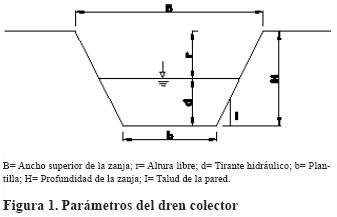
Para calcular estas dimensiones se utilizan las siguientes ecuaciones:
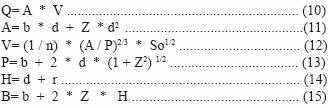
donde:
Q= Caudal de drenaje (m3 s–1); A= Área transversal de conducción (m2); V= Velocidad del flujo (m3 s–1); b= Plantilla (m); d= Tirante hidráulico (m); Z= Talud de la pared (adim); n= Coeficiente de rugosidad de Manning (adim); P= Perímetro mojado (m); So= Pendiente de la rasante (m•m–1); H= Profundidad de la zanja (m); r= Altura libre (m); B= Ancho superior de la zanja (m).
RESULTADOS Y DISCUSIÓN
En el Cuadro 1 se muestran los tiempos de drenaje (td), lluvias de diseño (LLd) e infiltraciones en los tiempos de drenaje (Itd) obtenidas por la multiplicación de la infiltración del suelo (3 mm/h) por el tiempo de drenaje (td), los escurrimientos (E) para el td (Etd) y 24 h (E24) estimados por el método del Balance Hídrico; se consideró la evapotranspiración de los cultivos en estudio (Etmax), calculada por el método de Blaney–Criddle (Norero, 1976). El tiempo de drenaje indica el máximo de horas que los cultivos soportan estar inundados (FIRA, 1985).
En el área a sembrar de chile, el flujo superficial total (E) para las 8 y 24 h fue de 48.13 mm; por la sensibilidad del cultivo a los excesos de humedad se consideró el mismo valor en ambos casos (Etd y E24); por lo anterior, necesita ser drenado en un td inferior a 24 h (Cuadro 1). En el pasto, que es el cultivo menos sensible a inundación, para td de 72 h el escurrimiento en el tiempo de drenaje (Etd) fue 71.45 mm y el escurrimiento en 24 h (E24) fue 23.82 mm. Lo anterior demuestra que en el área cultivada con pasto, a pesar de tener un escurrimiento superficial mayor para 72 h y menor para 24 h que el área sembrada con chile, las secciones hidráulicas de los drenes serán menores, debido a que el td requerido para evacuar los excesos de lluvia es superior. Los mayores valores de flujo superficial en 24 h se obtuvieron para el cultivo del frijol, siendo 2.32 veces mayor con respecto al cultivo del chile.
Los gastos de diseño calculados difieren en los cuatro cultivos a establecer, el menor valor fue para el cultivo de pasto con 0.43 m3 s–1 y el mayor correspondió a frijol con 1.68 m3 s–1, esto se debió a que la superficie a sembrar de frijol y el escurrimiento superficial en 24 h fue superior al resto de los cultivos en estudio (Cuadro 1).
En el Cuadro 2 se observan los valores del flujo superficial para 24 h calculados por el método CN, para un suelo de textura arcillosa, de infiltración muy lenta, grupo de suelo D, CN de 87 (en el pasto NC= 80) y condiciones hidrológicas buenas.
Al comparar los gastos de diseño (Q) entre los cultivos, se observó que la superficie sembrada con chile tuvo el valor más bajo 0.55 m3 s–1 (Cuadro 2), mientras que el área cultivada con frijol alcanzó el máximo valor con 2.12 m3 s–1, lo que obliga a diseñar sistemas de drenaje con secciones hidráulicas de mayor magnitud. El pasto fue el segundo cultivo con valores de flujo superficial y descarga de diseño más bajo, alcanzando valores de 79.37 mm y 0.89 m3 s–1, esto se debe a que posee el mayor tiempo de drenaje, el cual incide inversamente sobre los cálculos del coeficiente de drenaje.
La estimación del gasto de diseño por el método Racional Modificado se muestra en el Cuadro 3, variando el coeficiente C entre 0.6 y 0.4 según los cultivos y características de las zonas agrícolas. En el área cultivada con chile y pasto se obtuvieron valores de Q igual a 0.52 y 0.57 m3 s–1, mientras que en el área sembrada con frijol se reportaron los mayores valores con 2.27 m3 s–1, lo que indica que el agua a evacuar de la zona de frijol es mayor con relación a chile y pasto.
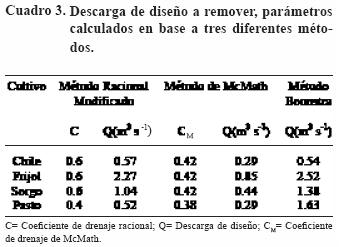
El Cuadro 3 muestra los parámetros requeridos para el método de McMath, siendo los valores de coeficiente de vegetación (C1) de 0.16 para todos los cultivos excepto el pasto que fue de 0.12, coeficiente de suelo (C2) de 0.22 y topografía (C3) de 0.04 respectivamente, estimandose el coeficiente de escurrimiento de McMath (CM) CM= C1+C2+C3.
Al igual que en los demás métodos de cálculo de descarga de diseño, el área sembrada con frijol mostró los mayores valores con 0.85 m3 s–1 (Cuadro 3) y los menores coinciden en los cultivos de chile y pasto, siendo éste de 0.29 m3 s–1. Estas diferencias en las descarga de diseño se deben fundamentalmente a la magnitud de la lluvia de diseño y el área a sembrar en cada caso.
En el Cuadro 3 se tienen los valores de descarga de diseño calculados por el método de Boonstra, siendo el hidromódulo de descarga de 125 mm/día. Aunque los mayores valores de Q coincidieron con el área cultivada de frijol (2.52 m3 s–1) y los menores con la zona sembrada con chile (0.54 m3 s–1) (Cuadro 3), no siguió la tendencia de los demás métodos evaluados, ya que obtuvo un hidromódulo de descarga que fue igual para todos los cultivos por considerarse solamente el coeficiente de almacenamiento en el suelo, el cual no fue determinado "in situ", además no incluyó parámetros importantes para la estimación de la descarga de diseño como son: tiempo de drenaje, condiciones de vegetación y topografía, entre otros.
La utilización del método Racional Modificado para la estimación de la descarga de diseño en los cultivos con td menor o igual a 24 h, por lo general conlleva a un sobredimensionamiento de la sección hidráulica del dren colector, mientras que para td mayores de 24 h tiende a un subdimiensionamiento de los mismos (Cuadro 3). Esto se debe a que en la mayoría de las áreas agrícolas no existen datos de intensidades de lluvia y por tanto se toma una relación entre la lámina total caída y el tiempo de drenaje, además las pendientes de las áreas agrícolas son por lo general pequeñas, no se tiene en cuenta el efecto del almacenamiento superficial y su principio se basa en considerar una lluvia de intensidad uniforme para toda la cuenca, durante un tiempo igual al tiempo de concentración; resultados similares mencionaron Linsley (1977) y Smedema y Rycroft (1988).
En la fórmula de McMath los valores que se obtuvieron para la descarga de diseño (Cuadro 3) fueron menores que el resto de los valores obtenidos por los otros métodos. Esto se debe a que la fórmula tiene en cuenta el factor de reducción de área, el cual influye en los resultados para áreas pequeñas, coincidiendo con lo planteado por Batista (1983), que recomienda su empleo para cuencas mayores de 200 ha.
Al comparar las láminas de agua máximas y mínimas de las áreas sembradas de chile y pasto obtenidas por los métodos de Balance Hídrico y por el NC, se encontró que los flujos superficiales en 24 h calculados por el primero fue 6.13 mm mayor al número de curvas en el cultivo de chile y lo estimado por el NC fue 55.55 mm mayor al Balance Hídrico para el cultivo de pasto. Estas diferencias pueden ser debido a que el NC considera aspectos agronómicos, edáficos y condiciones hidrológicas, y el Balance Hídrico reconoce la evapotranspiración máxima y la infiltración del agua en el suelo; éste último es un fenómeno complejo que está regulado por innumerables factores como espacio poroso, grado de dilatación de los coloides del suelo, contenido de materia orgánica, duración de la lluvia, la temperatura del suelo y agua, factores difíciles de controlar (Kramer, 1974). Se encontró que la infiltración, del agua de lluvia en el cultivo de chile fue menor que en el cultivo de pasto como se muestra en el Cuadro 1.
Para el dimensionamiento de los drenes se utilizaron los flujos superficiales calculados por el método NC por considerar las propiedades físicas y agronómicas del suelo. Para el cultivo de chile fue de 0.55 m3 s–1, dicho valor fue menor en 1.57, 0.60 y 0.34 m3 s–1 a los cultivos de frijol, sorgo y pasto, respectivamente (Cuadro 4). Las diferencias de gastos encontradas en los cuatro cultivos, tienen que ver con los tiempos de drenaje definidos ya que el agua en la superficie se mueve obedeciendo la fuerza de la gravedad y a una carga de presión. Según Herrera et al. (1999), cuando el espesor de la capa de agua a remover de la superficie del suelo es muy pequeño (velocidad despreciable), entonces, el flujo puede ser considerado flujo gradualmente variado y puede ser descrito adecuadamente por la ecuación de continuidad derivado del principio de conservación de la masa y la ecuación dinámica.
Las secciones hidráulicas del dren parcelario, del área a cultivar de frijol fue 2.62 m2, siendo 1.26 y 1.66 veces mayor a la superficie a sembrar de pasto y chile respectivamente (Cuadro 4).
CONCLUSIONES
Se determinó que el escurrimiento superficial por hectárea a evacuar de los cultivos fueron: 2.12 m3 s–1 frijol; 1.15 m3 s–1 sorgo; 0.89 m3 s–1 pasto y 0.55 m3 s–1 chile.
Se determinó que el escurrimiento superficial por hectárea a evacuar del cultivo chile fueron 1.57, 0.60 y 0.34 m3 s–1 menores a los cultivos de frijol, sorgo y pasto.
De cinco métodos aplicados para estimar los flujos superficiales (E24), el método de Número de Curva fue adecuado para diseñar las secciones hidráulicas de los drenes colectores, por considerar aspectos hidrológicos, edáficos y agronómicos del área de estudio.
LITERATURA CITADA
Aparicio M., F. 2004. Fundamentos de hidrología superficial. Limusa. México, D. F. 303 p. [ Links ]
Batista M., J. 1983. Escurrimiento superficial. Corporación de Desarrollo del Valle de San Francisco (CODEVASF). Brasilia, Brasil. [ Links ]
Becerra M., A. 1999. Escorrentía, erosión y conservación de suelo y agua. Universidad Autónoma Chapingo. Departamento de Publicaciones. Chapingo, Estado de México, México. p. 50–77. [ Links ]
Boonstra, J. 1989. Rainfall runoff relations I. In: Syllabus of the 28th International Course on Land Drainage. ILRI, Wageningen, The Netherlands. [ Links ]
Carrillo A., E.; Nájera H., F.; Palacios V., O. L. y Landeros S., C. 2001. Evaluación agrícola de un módulo de drenaje subsuperficial controlado en la Chontalpa, Tabasco. In: Simposio de Drenaje y Salinidad Agrícola. Memorias del XI Congreso Nacional de Irrigación. Guanajuato, México. p. 49–57. [ Links ]
Coras, M. P. 2000. Riego por aspersión. Universidad Autónoma Chapingo, Departamento de Fitotecnia. Chapingo, Estado de México, México. 209 p. [ Links ]
Coras, M. P. 2003. Propiedades físicas del suelo relacionadas con el riego. Universidad Autónoma Chapingo, Departamento de Publicaciones. Chapingo, Estado de México, México. 203 p. [ Links ]
Fideicomisos Instituidos en Relación a la Agricultura (FIRA) 1985. Riego y drenaje. Instructivos técnicos de apoyo para la formulación de proyectos de financiamiento y asistencia técnica. Banco de México, Subdirección de Evaluación de Proyectos y Asistencia, División de Agricultura. México, D. F. p. 27–32 (Serie de Agricultura Vol. 2). [ Links ]
Herrera, J.; López, G. y Reyes, J. 1999. Consideraciones sobre el diseño de las redes de drenaje superficial. Centro de Hidrología y Calidad de las Aguas, Instituto de Investigación de Riego y Drenaje (CENHICA–IIRD). Ciudad Habana, Cuba. [ Links ]
Instituto Mexicano de Tecnología del Agua (IMTA) 2000. Extractor rápido de información climatológica. ERIC. Ver. 2.0 Jiutepec, Morelos, México. [ Links ]
Instituto Nacional de Estadística Geografía e Informática (INEGI) 1999. Anuario estadístico de Tabasco. México. [ Links ]
Kessler, J. y Road, J. 1978. Análisis de los datos pluviométricos. In: Principios y Aplicaciones del Drenaje. Tomo III. Estudio e investigaciones. ILRI, Wageningen, Holanda. p. 16–57. [ Links ]
Kraijenhoff, D. A. y Van De Seur. 1977. Relación lluvias escorrentía y modelos para el cálculo. In: Principios y aplicaciones de drenaje. Vol. II. ILRI Internacional Institute for Land Reclamation and Improvement. Wageningen, Holanda. p. 263–342. [ Links ]
Kramer, J. P. 1974. Relaciones hídricas de suelo y planta. Edutex. México, D. F. 538 p. [ Links ]
Linsley, K. R. 1977. Hidrología para ingenieros. McGraw Hill. México, D. F. 385 p. [ Links ]
López, G. 1995. Estimación del escurrimiento superficial en una cuenca llana con vistas al cálculo de la capacidad de drenaje. Ingeniería Hidráulica en México. 16(2–3):48–53. [ Links ]
Luthin, J. N. 1977. Drenaje de tierras agrícolas. Teoría y aplicaciones. Limusa. México. 684 p. [ Links ]
Martínez, B. J. 1986. Drenaje agrícola, Vol. I. Ministerio de Agricultura, Pesca y Alimentación, España. 239 p. [ Links ]
Monteagudo, O. 1981 Recomendaciones sobre el cálculo del módulo de drenaje. Voluntad Hidráulica 18(56):12–15. [ Links ]
Norero, S. A. 1976. Evaporación y transpiración, Capítulo 4. Preparado para el curso de conservación de aguas y tierras. Centro Interamericano de Desarrollo Integral del Agua y Tierra CIDIA. Mérida, Venezuela. [ Links ]
Pizarro, F. 1985. Drenaje agrícola y recuperación de suelos salinos. 2a. ed. Agrícola Española. España. 521 p. [ Links ]
Rojas, M. 1976. Drenaje superficial de tierras agrícolas. Centro Interamericano de Desarrollo Integral de Agua y Tierra CIDIA. Venezuela. 93 p. [ Links ]
Rojas, M. 2002. Diseño de drenaje superficial local. Universidad Autónoma Chapingo, Departamento de Irrigación. Chapingo, Estado de México, México. p. 11–28. [ Links ]
Soil Conservation Service (SCS). 1972. National engineering handbook. Hydrology Section 4, Chapter 4–10. p. 19. [ Links ]
Smedema, L. K. and Rycroft, D. W. 1988. Land drainage: planning and design of agricultural drainage systems. Batsford Ltd. London. [ Links ]














