Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista internacional de contaminación ambiental
versión impresa ISSN 0188-4999
Rev. Int. Contam. Ambient vol.25 no.1 Ciudad de México feb. 2009
Simulación matemática de un digestor anaerobio tipo tanque agitado para el tratamiento de vertidos residuales
Mathematical simulation of an anaerobic shaken type tank digestor for the treatment of residual spills
Jorge DEL REAL OLVERA1, Francisco PRIETO GARCÍA2,*, Eva María SANTOS LÓPEZ2, Alma Delia ROMÁN GUTIÉRREZ2 y Alberto José GORDILLO MARTÍNEZ2
1 Facultad de Ingeniería Química, Universidad Veracruzana, Zona Xalapa, Circ. Aguirre Beltrán s/n, Xalapa, Veracruz, México.
2 Centro de Investigaciones Químicas, Universidad Autónoma del estado de Hidalgo, carretera Pachuca–Tulancingo, Km. 4.5 C.P. 42076, Pachuca, Hidalgo, México.* Correo electrónico: prietog@uaeh.reduaeh.mx
Recibido abril 2007
Aceptado septiembre 2008
RESUMEN
En los últimos años, el modelado matemático ha sido empleado para tratar de representar los cambios químicos que ocurren en el ambiente. Tradicionalmente los modelos se fundamentan en los balances de materia y la cinética química de los bioprocesos. En este estudio se aplican y simulan las ecuaciones obtenidas para un reactor biológico isotérmico tipo tanque agitado mediante ecuaciones lineales adimensionales en estado semi–estacionario. Para darle validez a los resultados derivados de la solución analítica, estos se comparan con los resultados experimentalmente obtenidos a nivel laboratorio para un digestor metanogénico en el régimen mesofílico de temperatura y en donde se trataron los vertidos residuales provenientes de una industria alcoholera bajo diferentes condiciones de operación, empleando como consorcio microbiano fluido ruminal vacuno. Los resultados del modelo concuerdan favorablemente bien con la producción de biogás y la disminución de la carga orgánica (expresada como DQO), teniendo un factor de ajuste promedio para ambos casos de R2=0.9960 y una variación del 0.01601, cuando se propone una cinética de reacción de primer orden y empleando en el medio células libres. Además que dicho modelo es capaz de predecir cuándo el sistema alcanza el estado estacionario.
Palabras clave: mesofílico, simulación matemática, metanogénico, bioproceso.
ABSTRACT
In the last years, mathematical modeling has been used to try to represent the chemical changes that occur in the environment. Traditionally the models are based on the mass balance and the kinetic chemistry of the bioprocesses. In this study the equations obtained for a biological isothermal reactor type shaken tank are applied and simulated by using adimensional linear equations in quasi–stationary state. In order to give validity to the results derived from the analytical solution, these are compared with the results experimentally obtained at laboratory level for a methanogenic digester in a mesophyll regime of temperature, used for treating residual effluents from the distillery industry under different operational conditions, using as microbial partnership bovine rumen fluid. The results of the model agree with the production of biogas and the reduction of organic charge (expressed like COD), having an average factor of adjustment for both cases of R2=0.9960 and a variation of 0.01601, when a kinetic reaction of first order is proposed, and using free cells in the environment. In addition this model is able to predict when the system reaches the stationary state.
Key words: mesophyllic, mathematic simulation, methanogenic, bioprocess.
INTRODUCCIÓN
Debido a la enorme complejidad que exhiben los procesos de degradación anaerobia es difícil desarrollar un modelo matemático que refleje su "realidad biológica". Esto ocasiona que los modelos existentes sean frecuentemente simplificaciones de dicha realidad. Sin embargo, el modelado y la simulación matemática se transforman en una herramienta útil para diseñar y evaluar el desempeño de sistemas digestivos. Debido a que la parte experimental es algo difícil y tediosa de realizar por los altos tiempos de reacción, no se dispone de abundantes datos, lo que genera que los estudios de modelado sean cada vez más necesarios. Una estrategia general del modelado involucra los siguientes pasos:
a. Modelar el proceso de degradación anaerobia de sustratos complejos, los fenómenos de transporte y los cinéticos–difusivos.
b. Integrar los resultados anteriores a un reactor ideal (discontinuo, tanque agitado o flujo pistón).
c. Considerar las desviaciones del patrón de flujo, geometría e hidrodinámica del sistema para modelar distintos tipos de reactores reales (lecho fijo, fluidizado, etc.)
Los primeros modelos que se desarrollaron sobre este tema (Andrews 1969, 1971, Buhr y Andrews 1977) contemplaban solamente la velocidad de degradación del ácido acético para describir la velocidad total de digestión de la materia orgánica (se asumió que la degradación del ácido acético era la etapa controlante).
El desarrollo de modelos matemáticos que describen el procesamiento anaerobio con consorcios de procedencia animal comenzó en la década de los años 70 debido a la necesidad ecológica de tratar los residuos de rastros en países de Europa Central. Entre los primeros trabajos realizados se encuentran los de Hill y Barth (1977), que incluyen modelos para la digestión de residuos de cerdos. En estos modelos se incorporan las etapas de hidrólisis y acidogénesis para estimar el efecto de la sobrecarga orgánica en la velocidad de metanización.
Boekhorst et al. (1981) señalan que los digestores anaerobios que utilizan residuos animales raramente operan en verdadero estado estacionario, son generalmente estados semi–estacionarios. Afirman que es el modelo dinámico el que posee la capacidad de predecir la respuesta del estado semi–estacionario y permite la optimización del proceso y un mejor diseño.
Angelidaki et al. (1993) presentan un modelo matemático para la degradación anaerobia de material orgánico complejo (estiércol) al igual que Hill (1982), con ciertas mejoras. El modelo incluye una etapa de hidrólisis enzimática y cuatro etapas biológicas, involucrando doce compuestos químicos. El amoníaco disuelto y el ácido acético constituyen los principales factores reguladores de su modelo propuesto.
Se sabe que para el diseño de digestores se requiere conocer la velocidad de reacción intrínseca en la superficie catalítica. Sin embargo, la concentración y la temperatura con la que se calculan éstas, se miden experimentalmente a la salida del reactor, lo cual no corresponde con las condiciones existentes en donde se está llevando a cabo la reacción ya que se ven afectadas por la hidrodinámica del sistema y la transferencia de masa. Lo anterior obliga a tener parámetros que ayuden a inferir las características cinéticas en la superficie catalítica. Experimentalmente los reactores químicos de tanque agitado son probablemente los sistemas más usados para la determinación de las constantes de velocidad de reacción. Para obtener la información cinética, es necesario planear adecuadamente los pasos experimentales, los cuales incluyen la resistencia a la transferencia de masa y calor, en el fluido y en los sólidos catalíticos (Marroquín et al. 2002). Los experimentos dinámicos se usan para la evaluación de parámetros tales como la constante de velocidad de reacción, las constantes de equilibrio y los coeficientes de transporte, asimismo permiten elucidar mecanismos de reacción por medio del análisis de respuesta de los reactores catalíticos heterogéneos a cambios en la concentración de alimentación.
Un procedimiento típico consiste en introducir una perturbación en la composición de la corriente de entrada y monitorear la respuesta en la corriente de salida (Datta y Rinker 1983). En este tipo de experimentos, la interpretación de los datos cinéticos puede ser incorrecta si las resistencias a la transferencia de masa no son consideradas, por lo tanto es necesario usar modelos que incluyan los efectos más importantes, para decidir cuales resistencias pueden ser despreciadas. El tratamiento de este problema se ha realizado considerando soluciones matemáticas aproximadas, de tal forma que se pueden mencionar en primera instancia aquellas en las que no se consideran las resistencias externas al transporte de masa.
Así se reporta por Towler y Rice (1974), quienes analizaron un sistema de dos fases en un reactor continuo de tanque agitado (RCTA). En su modelo consideran un sistema dinámico e isotérmico, con resistencias a la transferencia de masa interna pero no consideran la externa, ya que asumen que el sistema se encuentra bien mezclado. Las expresiones resultantes pueden ser útiles para la determinación de la difusividad efectiva y las constantes de velocidad de reacción, a partir de la medición de la concentración en la salida del reactor. Dichos autores presentan gráficas de concentración contra tiempo, en las cuales aparece un mínimo para ciertas combinaciones de los parámetros adimensionales que describen el sistema. Con base a este comportamiento, sugieren que este mínimo puede ser usado para la determinación de parámetros cinéticos; sin embargo, no dan las condiciones bajo las cuales puede obtenerse dicho punto. Por otro lado, Do y Rice (1982) presentan un estudio realizado a un sistema en el que se encuentran partículas catalíticas inmersas en un RCTA. Proponen que la reacción es de primer orden y consideran las resistencias a la transferencia de masa. Basados en la técnica de perturbación, determinan las condiciones para las cuales se presenta el mínimo reportado por Towler y Rice (1974), concluyendo que una condición para que lo anterior ocurra, es que el tiempo de residencia en el tanque sea mucho menor al tiempo de difusión en la partícula:

Debido a que tanto el volumen, como el flujo pueden controlarse experimentalmente, se pueden ajustar de tal forma que se cumpla la relación expresada anteriormente. Determinando el tiempo al cual ocurre el mínimo, se puede obtener la constante de velocidad de reacción.
Datta y Rinker (1983) reportan soluciones dinámicas que modelan un reactor tipo RCTA isotérmico en donde ocurre una reacción química de primer orden irreversible junto con difusión, tanto en las partículas catalíticas como en el líquido estancado. Las soluciones son obtenidas en forma general, no se especifica la forma de la partícula y el modelo incluye los efectos de las resistencias a la transferencia de masa externa (interfase sólido–fluido) e interna (en la intrapartícula).
Szukiewics (2000) propone un método aproximado basado en la fórmula LDF (Linear Driving Force) para un proceso de difusión–reacción. Dicha aproximación consiste en reemplazar la ecuación diferencial parcial del balance de masa en la partícula, por una ecuación diferencial ordinaria. Con esto, la solución se simplifica y en muchos casos los resultados obtenidos son una muy buena aproximación al modelo riguroso. Se considera al sistema en estado transitorio y la reacción de primer orden, con lo cual la ecuación que gobierna el transporte del reactivo en la partícula esférica es:

Marroquín et al. (2002) consideran también un RCTA en el cual se encuentran partículas catalíticas suspendidas en un fluido perfectamente mezclado, suponen un proceso isotérmico, una reacción de primer orden, donde además consideran las resistencias a la transferencia de masa internas y externas. El fenómeno de difusión–reacción es modelado en términos de ecuaciones de promedio volumétrico y para su resolución utilizan el método de la transformada de Laplace.
Szukiewicks (2002) continúa trabajando en métodos aproximados para problemas de difusión–reacción en estado transitorio mediante la aplicación de la formula LDF para cualquier tipo de expresión cinética. Cuando las cinéticas son no lineales, es necesario linealizarlas mediante series de Taylor, tal como lo sugieren Marroquín et al. (1999). El método obtenido presenta buena concordancia con la solución exacta para valores bajos del módulo de Thiele, el cual es el parámetro adimensional que relaciona la transferencia de masa y la cinética de reacción.
Chaudhari y Ramachandran (1980) presentan el análisis de un sistema trifásico en el cual ocurre una reacción de orden cero y consideran las resistencias externas e internas a la transferencia de masa. Su modelo es isotérmico y al igual que en la mayoría de los estudios reportados es en estado estacionario, aunque consideran la variación de la concentración del reactivo en fase gas con respecto al espacio. En este trabajo se muestra que para este tipo de sistemas existe una concentración crítica de la fase gaseosa por debajo de la cual los efectos difusivos son de amplia importancia y en donde se presenta una zona sin reacción dentro de la partícula catalítica, debido a que la concentración del reactivo es igual a cero en algún punto dentro de ella. Entre las expresiones analíticas que presentan se encuentra la ecuación para determinar el valor del factor de efectividad (como su nombre lo indica este parámetro estima la eficiencia o eficacia de la partícula catalítica en el proceso) que es:

Chang (1982) considera un problema de difusión–reacción isotérmico en estado estacionario en el que se presenta una cinética del tipo de Michaelis–Menten, incluyendo los efectos de las resistencias a la transferencia de masa interna y externa. En dicho trabajo se propone un método de cálculo para la evaluación del factor de efectividad a valores altos del módulo de Thiele. El método propuesto utiliza expresiones analíticas para calcular los perfiles de concentración empleando una cinética de primer orden como aproximación a la región en la cual se presenta la dificultad numérica.
A pesar de las diversas soluciones aproximadas que se han desarrollado, el problema sigue siendo de gran interés debido a que dichas soluciones propuestas están restringidas a casos particulares. El interés fundamental para el desarrollo del presente modelo matemático, se justifica por la falta de modelos generales que permitan describir el comportamiento de los sistemas digestivos anaerobios en el tratamiento de vertidos residuales. Se considera que la reacción química se realiza en un digestor trifásico, continuo tipo tanque agitado el cual contiene al consocio microbiano del fluido ruminal representado como partículas catalíticas porosas, suspendidas por la acción de un fluido perfectamente mezclado (Fig. 1). El reactivo A (sustrato), se alimenta en la fase líquida y se transporta hasta los poros del catalizador, en donde reacciona de acuerdo al modelo de Michaelis–Menten y de los principales productos es el biogás que abandona el sistema.

Para que cualquier especie química alimentada en el sustrato pueda reaccionar sobre la superficie activa del catalizador, debe ocurrir (Fig. 2):

1) Transporte del reactivo A desde el seno del líquido a la superficie catalítica, CA
2) Transporte difusivo en la intrapartícula a través de los poros catalíticos, CAS
3) Adsorción del reactivo A en los sitios activos del catalizador, CAi
4) Reacción superficial heterogénea de A para la conversión en productos, CRt
5) Desorción de los productos de los sitios activos, CRS
6) Difusión del producto a través de los poros, CRSE
7) Transporte del producto de la superficie catalítica al seno del líquido., CR
En la figura 3 se muestra el perfil de concentración generado para una especie que exhibe una reacción irreversible en un reactor continuo de tanque agitado. La zona intermedia entre el seno del fluido y el sólido representa una película de líquido estancado (capa límite) donde se manifiestan las resistencias externas a la transferencia de masa.

Debido a que las partículas tienden a moverse con el líquido, existe poca velocidad relativa entre el sólido y el líquido presentes en la suspensión, originando una capa límite casi inmóvil alrededor de las partículas. Dicha capa provoca que el reactivo deba ser transferido por difusión a través de ella para llegar a la superficie del catalizador. Esta resistencia al transporte del reactivo resultará en una diferencia de concentraciones, entre el seno del fluido y la superficie catalítica, la cual puede retardar significativamente la velocidad global de reacción. Finalmente, debido a que la conductividad térmica de los líquidos es relativamente alta, incrementa el coeficiente de transferencia externo de calor. Con esto y la baja generación de calor en las reacciones biológicas, se puede afirmar que se mantienen condiciones isotérmicas. Por tanto, las diferencias externas e internas de temperatura pueden despreciarse (Smith 1986).
Con base en lo mencionado anteriormente, se establecen las siguientes suposiciones para el modelo:
• El sólido es esférico.
• El tamaño de la partícula es homogéneo.
• El fluido está perfectamente mezclado.
• Se lleva a cabo un proceso isotérmico.
• La velocidad de desaparición del reactivo (sustrato) en la superficie de las partículas porosas obedece a una cinética del tipo de Michaelis–Menten.
• No existe reacción alguna en la fase gaseosa.
• No se consideran los efectos debidos a la desactivación (muerte) ni generación (crecimiento) de la biomasa.
Debido a que el fluido está perfectamente mezclado, es razonable considerar que el transporte de masa en las partículas ocurre sólo en la dirección radial.
MATERIALES Y MÉTODOS
Las vinazas fueron colectadas en la planta destiladora "La Aurora" ubicada en el municipio de Actopan, Veracruz, la cual utiliza jugo natural de caña para obtener el alcohol. El cultivo primario de bacterias se obtuvo del fluido ruminal vacuno. La oxidación biológica anaerobia se llevó a cabo en un digestor de vidrio de 4 litros, agitado mecánicamente y operado por lotes a una temperatura de 35 ± 2 °C y 250 rpm. El proceso digestivo con células libres, se inicia con 0.5 litros de inóculo metanogénico y se añaden 2.5 litros de vinaza neutralizada y diluida con la finalidad de adaptar a los microorganismos a su nuevo ambiente (del Real et al. 2007). Los parámetros analizados fueron, cantidad de biogás generado, demanda química de oxígeno (NMX–AA–030–SCFI–2001) y pH del vertido contaminante, analizado y estabilizado para asegurar que se trabaja en condiciones metanogénicas (NMX–AA–008–SCFI–2000).
El proceso de difusión–reacción es modelado en términos de ecuaciones de transporte promedio de materia como lo propone Whitaker (1999). Las ecuaciones de balance para cualquier componente se describen:
Para la fase líquida:

para la fase gaseosa:

la fase sólida está descrita por:

siendo εβ la fracción porosa de partículas; es decir, el espacio no cubierto por la fase sólida ni la fase gaseosa, mientras que Def es la difusividad efectiva, r es la variable radial de la partícula y CAi es la concentración intrínseca promedio en las partículas definida por Whitaker (1999). Los números adimensionales propuestos para llegar a la solución del problema se definen como:
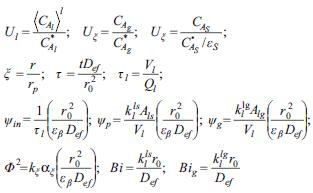
Lo que da como resultado las siguientes ecuaciones adimensionales:
Para la fase líquida:

Para la fase gaseosa:

y para la fase sólida:

Con las consecuentes condiciones de frontera adimensionales:

Una vez acopladas las correspondientes condiciones de frontera y resolviendo el sistema de ecuaciones se obtienen los siguientes resultados:
En la fase gaseosa:

En la fase líquida:

En la fase sólida:

RESULTADOS Y DISCUSIÓN
Los resultados obtenidos al simular las expresiones analíticas adimensionales que describen los perfiles de concentración para el problema de difusión–reacción isotérmica, se muestran a continuación. Para ello se ha seguido el modelo propuesto por Whitaker, considerando una cinética del tipo Michaelis–Menten y en estado semi–estacionario. Se presenta también el comportamiento del factor de efectividad calculado para la partícula catalítica involucrada en este estudio. El primero de los perfiles adimensionales generado con el modelo describe el comportamiento que tiene la concentración del gas a través del tiempo (ecuaciones 1 y 2). La figura 4, muestra una curva hiperbólica ascendente la cual llega a un estado de equilibrio final. Esto sugiere que en un principio el biogás se estará formando dentro del digestor de manera cambiante durante una primera etapa, pero posteriormente llega a ser una cantidad fija la que se genera. Dicho comportamiento hace suponer que después de esa primera etapa, se llega a un estado estable para este producto de reacción.

Como se ha indicado, la reacción química se está llevando a cabo sobre la superficie catalítica, es decir en los microorganismos, los cuales son considerados por el modelo como partículas esféricas porosas en suspensión, como una aproximación matemática. Los resultados obtenidos para este parámetro junto con los problemas difusionales externos de masa se muestran en la figura 5.

Se puede observar cómo los problemas externos a la transferencia de masa, generan que la concentración de sustrato que llega a la superficie catalítica sea inferior al 50% (al inicio de la curva); se sugiere que el sistema, aun cuando está perfectamente mezclado, no puede evadir los problemas de transporte, los cuales no se toman en cuenta en muchos de los modelos propuestos en la literatura y en este caso sí se hace. Por otro lado, los problemas internos son también importantes ya que casi el 40 % del sólido catalítico está desaprovechado, la concentración del sustrato hacia dentro del sólido decae drásticamente, llegando a ser cero aproximadamente al 24 %. Dicho comportamiento indica que un sistema con soporte catalítico incluido trabajará de manera más eficiente ya que tendrá menos problemas difusivos hacia el interior de la partícula. Con este mismo razonamiento, resulta lógico pensar que la eficiencia del biocatalizador es baja gracias a los diversos problemas de transporte de materia. La curva que muestra el factor de efectividad (η) con respecto al radio (ecuación 3) se muestra en la figura 6.

Esta curva de efectividad confirma el comportamiento anterior, ya que conforme se analiza el fenómeno hacia el interior del poro la eficacia de la reacción disminuye significativamente. Para darle validez a los perfiles teóricos calculados por el modelo, se comparan estos con los reportados en trabajos anteriores (del Real et al. 2007) de manera experimental en un digestor anaerobio. Los parámetros comparados son la concentración de biogás generado (Fig. 4) y la disminución de la carga orgánica, expresada como DQO (Fig. 5). Para el primer caso, se muestra como cambia la concentración de biogás con el tiempo (Fig. 7).

Para este caso el ajuste de ambas curvas fue excelente, indicando que el comportamiento de este parámetro puede ser perfectamente predicho con el empleo de este modelo y sus consideraciones anteriormente explicadas. El factor de ajuste o coeficiente de regresión obtenido que fue R2=0.9960 con una variación mínima de datos, así lo demuestra.
Finalmente, se compararon los datos de disminución de DQO (Fig. 5) obtenidos por ambos métodos. Dichos resultados se muestran en la figura 8, donde se observa que la tendencia de ambos comportamientos es muy semejante, llegando a un estado estable al final del proceso. Para este caso los valores calculados para el factor de ajuste fueron de R2=0.9943 lo cual hace muy favorable el empleo del modelo aquí propuesto para predecir o estimar la eficiencia del tratamiento de vertidos residuales.

CONCLUSIONES
Se puede afirmar que de acuerdo con datos reportados previamente (del Real et al. 2006), por el grado de DQO disminuido y la generación de biogás en el sistema de biodegradación Vinaza–Fluido ruminal, se justifica la aplicación de este modelo con fines netamente ambientales. De igual manera se puede implementar dicho modelo para cálculos de ingeniería, ya que ofrece la posibilidad de manejo de variables para lograr con esto, condiciones óptimas del proceso digestivo incrementando así el desempeño del biorreactor y estimar además, el tiempo necesario para obtener la estabilidad.
REFERENCIAS
Andrews J.F. (2005). Dynamic model of the anaerobic digestion process. J. San. Eng. Div. Proc. Am. Soc. Civ. Eng. SA 1, 95–116. [ Links ]
Andrews J.F. (1969). Microbial adherence studies for anaerobic filters. J. San. Eng. Div. Proc. Am. Soc. Civ. Eng. 95, 95. [ Links ]
Angelidaki I., Ellegaarg L. y Ahring B. (1993). A mathematical model for dynamic simulation of anaerobic digestion of complex substrates: focusing on ammonia inhibition. Biotech. Bioeng. 42, 159–166. [ Links ]
Boekhorst R.H., Ogilvie J.R. y Pos J. (1981). An overview of current simulation models for anaerobic digesters. En: Livestock waste: A renewable resource. (R.J. Smith, Ed.) ASAE Publication N° 2–81. ASAE, St. Joseph, MI. p. 85. [ Links ]
Burh H.O. y Andrews J.F. (1977). The thermophilic anaerobic digestion process. Wat. Res. 11, 129–143. [ Links ]
Chang H.N. (1982). Numerical calculation of effectiveness factors for the Michaelis–Menten type kinetics with high Thiele moduli". AIChE J. 28, 1030–1032. [ Links ]
Chaudhari R.V. y Ramachandran P.A. (1980). Three phase slurry reactors. AIChE J. 26, 177–201. [ Links ]
Datta R., Rinker R.G. (1983). Transient response of three–phase slurry reactors. Chem. Eng. Sci. 39, 893–901. [ Links ]
del Real J., Prieto F., Santos E.M., Román A.D. y Gordillo A.J. (2007). Biocinética y modelado dinámico de la degradación anaerobia de vinazas de jugo de caña. Rev. Ing. San. Amb. 90, 36–44. [ Links ]
Hill D.T. y Barth C.L. (1977). A dynamic model for simulation of animal waste digestion. J. Wat. Pollut. Control Fed. 10, 2119–2143. [ Links ]
Hill D.T. (1982). A comprehensive dynamic model for animal waste methanogenesis. Transactions of the Am. Soc. of Agricul. Eng. 0001–2351/82/2505, p.1374. [ Links ]
Marroquín de la Rosa J.O., Morones Escobar R., Viveros García T. y Ochoa Tapia J.A.(2002). An analytic solution to the transient diffusion–reaction problem in particles dispersed in a slurry reactor. Chem. Eng. Sci. 57, 1409–1417. [ Links ]
Marroquín J.O., Viveros T. y Ochoa J.A. (1999). A linear approximation method to evaluate isothermal effectiveness factors. Chem. Eng. Comm. 174, 53–60. [ Links ]
Norma Mexicana. NMX–AA–008–SCFI–2000. Que establece la metodología para la determinación del pH en aguas residuales. Secretaría de Comercio y Fomento Industrial, México. [ Links ]
Norma Mexicana. NMX–AA–030–SCFI–2001. Que establece la metodología para la determinación de la demanda química de oxígeno mediante la digestión de la muestra con dicromato. Secretaría de Comercio y Fomento Industrial, México. [ Links ]
Smith J.M. (1986). Ingeniería de la cinética química. Mc. Graw Hill. México. p. 47. [ Links ]
Szukiewicz M.K. (2000). New approximate model for diffusion and reaction in a porous catalyst. AICHE J. 46, 661–665. [ Links ]
Szukiewicz M.K. (2002). An approximate model for diffusion and reaction in a porous pellet. Chem. Eng. Sci. 57, 1451–1457. [ Links ]
Towler B.F. y Rice R.G. (1974) A note on the response of a CSTR to a spherical catalyst pellet. Chem. Eng. Sci. 29, 1828–1832. [ Links ]
Whitaker S. (1999). The method of volume averaging. Kluwer Academic Publishers. EUA, p. 67. [ Links ]














