Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Atmósfera
versión impresa ISSN 0187-6236
Atmósfera vol.17 no.3 Ciudad de México jul. 2004
The mechanical influence of continental topography on the trajectories
of tropical cyclones near the west coast of México
L. Zavala Sansón
Departamento de Oceanografía Física, CICESE
Km 107 Carretera Tijuana-Ensenada, 22860 Ensenada, Baja California, México
lzavala@cicese. mx
RESUMEN
La evolución de ciclones tropicales en el Pacífico Norte oriental es estudiada por medio de un modelo barotrópico con topografía continental. El objetivo es investigar la trayectoria de vórtices ciclónicos en esta área cuando son afectados solamente por los efectos β planetario y topográfico. Este último se debe a la pendiente de la orografía continental e induce la deriva del vórtice en la dirección "noroeste" local, la cual coincide con el noroeste geográfico (debido a la orientación de la topografía). Un claro resultado de la combinación de estos dos mecanismos es el aumento de la rapidez de deriva del ciclón. La dirección precisa de la trayectoria depende de la posición inicial con respecto al continente. Los vórtices que inician al sureste de la región de estudio (alrededor de 12° N, 95° O) son desviados hacia el oeste por la Sierra Madre del Sur, y siguen una trayectoria casi paralela al continente. Cuando los vórtices comienzan a latitudes mayores de 15° N, su movimiento se debe principalmente al efecto β planetario, acercándose al continente, hasta que son atraídos hacia la Sierra Madre Occidental a mayores latitudes. Estos resultados sugieren la posible influencia de la orografía continental en las trayectorias de algunos ciclones tropicales observados en esta región.
ABSTRACT
The evolution of tropical cyclonic vortices on the eastern North Pacific is examined by means of a barotropic model with an idealized continental topography. The aim of the study is to investigate the trajectories of cyclones in this area affected by both the topographic and the planetary β effects. The topographic β effect is mainly due to the ascending slope of the orography, and induces the vortex to drift towards local "northwest" direction, which coincides with the geographical northwest (because of the topography orientation). As a result, the vortex drift is clearly enhanced when both effects are considered. The precise direction of the trajectory depends on the initial geographical position with respect to the continent. Vortices initialized at southeastern areas (around 12° N, 95° W) are deflected by the Sierra Madre del Sur more to the west, following a trajectory almost parallel to the continent. For vortices initialized at 15° N or more, their drift is mainly due to the planetary β effect, although eventually they are attracted towards the Sierra Madre Occidental at higher latitudes. These conclusions suggest the possible influence of orography on the trajectories of real tropical cyclones in this area.
Key words: Tropical cyclones, Northeast Pacific, continental topography, hurricanes.
1. Introduction
This paper addresses the influence of continental orography on the motion of tropical cyclones produced in the eastern North Pacific, near the west coast of Mexico. It is well known that this is one of the most hurricane prolific areas during summer and early autumn in the Northern Hemisphere. The motion of such vortices is therefore a fundamental problem in atmospheric sciences that needs to be understood, since they transport important physical properties such as momentum, heat and humidity during their drift, and because of their strong impact on populated areas. The combination of different phenomena affecting the evolution of tropical cyclones, however, makes their motion difficult to interpret. Some of these processes are, for instance, the influence of large-scale zonal flows (Holland, 1983; DeMaria, 1985), vortex size and structure (Fiorino and Elsberry, 1989), and the thermodynamic properties of the atmosphere-ocean interaction along the genesis and evolution of cyclones (Emanuel, 1999). In particular, the β effect in the Northern Hemisphere (associated with the latitudinal variation of the Coriolis parameter) induces cyclonic vortices to drift northwestward (see, e. g., Adem, 1956; Chan and Williams, 1987). In the present paper, the influence of the continental topography on the motion of an idealized vortex is studied by means of a dynamical model, that is, without taking into account its thermo-dynamical nature. The aim is to isolate the mechanical influence of the topography on the trajectory of barotropic vortices, and to determine which cyclones (with a given strength and initial position) are prone to be affected by topographic effects.
There are important previous results directly related with the present study. In particular, Zehnder (1993) and Zehnder and Reeder (1997) have pointed out the possible influence of the Sierra Madre in México on the drift of tropical cyclones, both in the eastern Pacific and in the Gulf of México. In both cases, their numerical results on barotropic vortices on a β-plane suggest that cyclones are apparently deviated toward the Sierra Madre, thus approaching the continent. A more basic study by Zavala Sansón (2002; hereafter ZS02) examined the evolution of a barotropic cyclone on a f-plane interacting with a topographic ridge by means of laboratory experiments and numerical simulations. The main results showed that, even in the absence of β, the purely topographic influence of the ridge is able to induce the vortex motion. Such behaviour is related with the ascending slope of the ridge, which imposes a topographic β-effect associated with the local "northwestern" direction, where the local "north" corresponds with the upslope direction. As a result, the vortex drifts towards the topography, with an additional component parallel to the ridge (i.e. with shallow water to the right). This is a well-known phenomenon related with potential vorticity conservation in a rotating fluid with a sloping bottom (see, e. g., van Heijst, 1994; Zavala-Sansón and van Heijst, 2000).
From a mechanical point of view, therefore, both the planetary and topographic β effects are responsible for the vortex motion due to the redistribution of vorticity as fluid columns move in the north-south directions (planetary effect) or in the uphill-downhill directions over the ridge (topographic effect). These are the essential mechanisms on the trajectory of a barotropic vortex, and they will be further discussed through out the paper.
The physical model considered here assumes a quasi two-dimensional, homogeneous flow on a rotating system, i. e., the fluid moves in columns that remain always vertical. Changes of vorticity are therefore associated with horizontal divergence of fluid due to variable topography and, less importantly, by lateral diffusion. This approach was also used in the numerical simulations of ZS02. The main differences in the present study are that (i) the planetary β-effect is included; (ii) although still idealized, the bottom topography closely resembles the size and orientation of the Sierra Madre; (iii) realistic atmosphere flow parameters are used; and (iv) bottom friction is ignored. It must be mentioned that the topography used here is formed by two superimposed ridges, representing the Sierra Madre Occidental (between 20 and 30° N), and the Sierra Madre del Sur (between 15 and 20° N), each of them with a different orientation. In other words, this paper examines the role of the topographic influence for a very specific region in the western Mexican coast, and the results are interpreted with the help of previously mentioned studies.
The rest of the paper is organized as follows. Section 2 contains the physical model, a description of the topography, the initial cyclones, and the basic scales governing the fluid motion. In section 3, the numerical results are presented, and section 4 contains a discussion and general conclusions.
2. The model
2.1 Governing equations
The physical mechanisms involved in the results described in this paper are governed by the barotropic relative vorticity equation on a β-plane. Written in the ζ-φ formulation, the evolution equation is
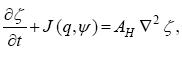 .......................(1)
.......................(1)
where ζ = δv/δx - δu/δy is the vertical component of the relative vorticity, with u = (u, v) the horizontal velocity vector with components in x (west-east) and y (south-north) directions, φ is the stream function, AH is the horizontal eddy viscosity, 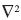 is the horizontal Laplacian operator, J is the conventional Jacobian operator, and q is the potential vorticity defined as
is the horizontal Laplacian operator, J is the conventional Jacobian operator, and q is the potential vorticity defined as
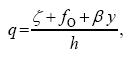 .................................(2)
.................................(2)
with f0 the Coriolis parameter at a reference latitude, b its latitudinal gradient, and h(x, y) is the local fluid height. Note that the time-independence of h implies that free-surface effects have been neglected in the continuity equation. In addition, bottom friction is not considered. Within this approximation the horizontal velocities are assumed to be depth-independent, and given by
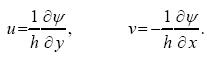 ..................(3)
..................(3)
Using these expressions it is verified that
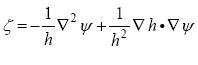 ....................(4)
....................(4)
It can also be noticed that the dynamic equation (1) can be written as
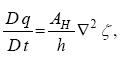 ...................................(5)
...................................(5)
(where D / Dt is the material derivative) showing that the inviscid limit, Dq / Dt = 0, expresses conservation of potential vorticity per fluid column.
2. 2 Bottom topography and initial vortex
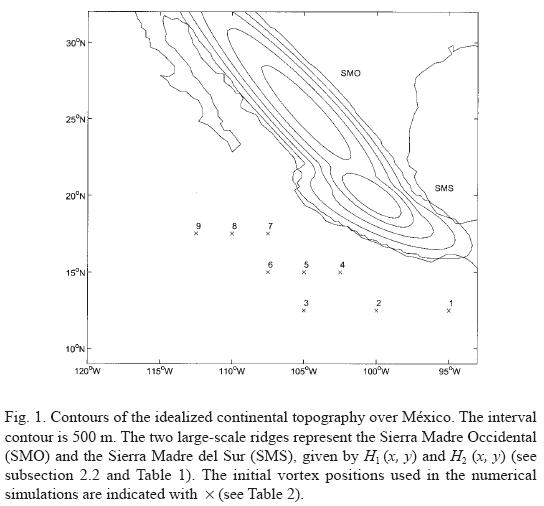
In order to resemble the orography over continental México, an idealized bottom topography based on the work of Zehnder (1993) is used. In that study, the topography is an ellipsoidal ridge, with the major semiaxis oriented in the same direction as the Sierra Madre. In the present case the topography is formed by two large-scale mountain ranges, as shown in Figure 1, in order to take into account the orientation of the Sierra Madre between 20 and 30° N (Sierra Madre Occidental, hereafter SMO) and between 15 and 20° N (Sierra Madre del Sur, SMS). The fluid height h is of the form
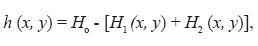 ....................(6)
....................(6)
where H0 is the maximum height. The two topographic features H1 and H2 represent the SMO and SMS, respectively, and they are given by:
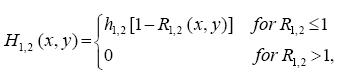 ....................(7)
....................(7)
where
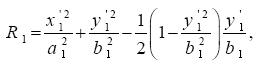 ...................................(8)
...................................(8)
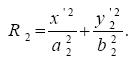 .............................................................(9)
.............................................................(9)
The (x'1,2, y'1,2) axis are the Cartesian directions rotated an angle α1,2:
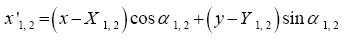 ...................(10)
...................(10)
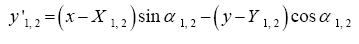 ................(11)
................(11)
Both topographies have an ellipsoidal shape with semiaxis a1,2 and b1,2, a maximum height of h1,2, and they are centred at (X1,2,Y1,2). Note that the SMO, given by H1 is not symmetrical with respect to the corresponding x'1 axis, but its maximum height is slightly shifted towards negative y'1. The parameters of the topography are given in Table 1. The central positions of the ridges (X1,2,Y1,2) are chosen such that the vortex is initially placed at the center of the domain in all simulations. Notice that the height is about 2,000 m (or even higher, at regions where both topographies are superimposed).

The initial condition in the simulations is a circular vortex with initial positions shown in Figure 1. The vortex azimuthal velocity distribution is approximated by
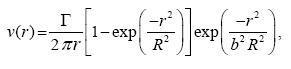 ....................(12)
....................(12)
where Γ is the vortex strength, R a horizontal length scale, r the radial distance to the center of the vortex, and b a nondimensional constant. This structure is a modified version of the so-called Lamb vortex (Saffman and Baker, 1979; see also Kloosterziel and van Heijst, 1992) wich is defined as
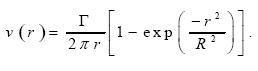 ............................(13)
............................(13)
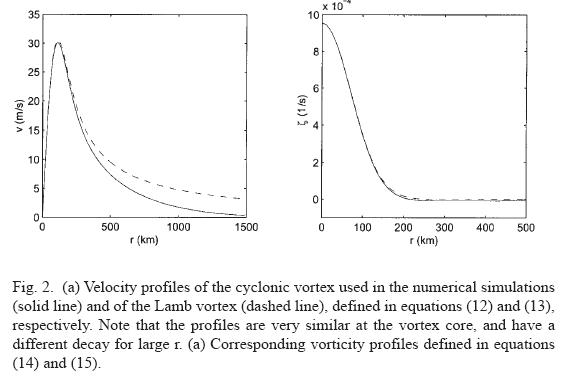
Figure 2 shows the radial profiles of the azimuthal velocity of the two vortices. It can be noticed that they are very similar for r <= R when the factor b is larger than unity (in the present case b = 10 ). The difference becomes important for r >> R, where the Lamb vortex decays as 1/r, whilst expression (12) decays exponentially due to the additional factor exp (-r2/b2R2). Vortex models applied to tropical cyclones present a similar behaviour (see e.g. Fiorino and Elsberry, 1989).
The vorticity profile is given by ζ = (1/r) δ(rv) /δr.
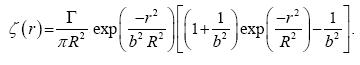 ....................(14)
....................(14)
For b >> 1 this is well approximated by the Lamb profile (see Figure 2)
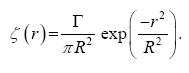 .......................................................(15)
.......................................................(15)
These vortices are non-isolated in the sense of having a single-signed vorticity. This is an important property that enhances the interaction with the topographic feature, even when the vortex is initially placed at a large distance (compared with R) from it (ZS02). The vortex parameters in all simulations are R=100 km and Γ = 3 x 107 m2s-1. Using these values, the maximum azimuthal speed is approximately 100 km/h, which corresponds with the typical speed of atmospheric cyclones.
2.3 Basic scales
The dynamic equation governing the fluid motion can be written as
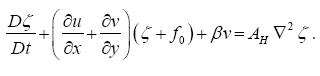 ....................(16)
....................(16)
A scale analysis provides an insight into the fundamental mechanisms governing the vortex motion. According with this expression, the production of vorticity per fluid column is given by the horizontal divergence, the b effect, and horizontal diffusion of vorticity. In this model, the horizontal divergence is only due to the bottom topography hB (x,y) = H1(x,y) + H2(x,y), and it can be written as
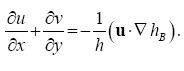 ................................................(17)
................................................(17)
This expression scales as Vrhr /HoW, where Ho is the total depth, W is the horizontal scale of the topography, hr its maximum height, and Vr is the typical azimuthal velocity over the ridge. As mentioned in ZS02, this is a suitable scale for the velocity only for the divergence term when the vortex is far from the ridge (i. e. at a distance Xo > R, with R the vortex lengthscale). In such a case, Vr << V, where V is the maximum azimuthal velocity. The vorticity equation is non-dimensionalized by using the vorticity V/R, the timescale 1/fo, and considering that Vr /V ˜ R/Xo, according with equation (13) for r >> R. This yields
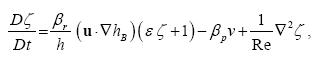 ..................................(18)
..................................(18)
where the nondimensional numbers are:
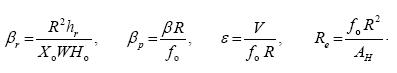 ....................(19)
....................(19)
Typical orders of magnitude for tropical cyclones are R≈100 km, and V≈30 m/s; the topographic parameters are approximately hr≈2 km, W≈200 km; the planetary parameters are fo≈5x10-5s-1:, β≈2x10-11(ms)-1; for the atmosphere, a total depth Ho≈5 km and an eddy viscosity AH≈104 m2s-1 are considered (Pedlosky, 1987; p. 185).
For the present purposes, the most important parameters are the topographic and the planetary β effects (represented by βr and βp, respectively). Using an initial distance Xo ≈ 500 km, the nondimensional β numbers are approximately βr, βp ≈ 0.04, that is, of the same order of magnitude. This indicates that the vortex trajectory is expected to be importantly influenced by both effects. Also, note that the topographic βr becomes dominant when the vortex is close to the topography, and negligible for vortices far from the continent.
Lateral viscous effects are given by the Reynolds number as 1/Re˜O(10-2), and they provide a weak damping through the simulation. For instance, the total kinetic energy for the entire domain diminishes only 18% in a typical simulation after 60 h. The strength of the vortex is measured by the Rossby number ε, which is initially O(1) and eventually becomes smaller as the vortex loses energy due to Rossby wave radiation and lateral friction. The maximum tangential velocity also decreases 18% approximately.
3. Numerical simulations
The barotropic vorticity model in the ζ - φ formulation is solved by means of a finite differences code. The original code was developed for purely two-dimensional flows by R. Verzicco and P. Orlandi, and later adapted by J. van Geffen. In order to include the effects of the topography, the relation between the relative vorticity and the stream function, equation (4), is solved by using a multigrid method from a NAG routine (Zavala Sansón et al., 1999; Zavala Sansón and van Heijst, 2000; ZS02).
The numerical domain is a 3990 km x 3990 km square with free-slip boundary conditions, which is discretised by 129 x 129 grid points. The dimensions of this domain are large enough to avoid the influence of lateral boundaries on the motion of the vortices. Additional numerical simulations were performed using two larger domains (squares with 5000 and 6000 km side length), and the obtained results were essentially the same. In all simulations, the initial position of the cyclones coincides with the center of the numerical domain. The domain represents a β -plane with longitudinal and latitudinal limits given by (-1995, 1995; -1995, 1995) km. The reference latitude is chosen as 16° N, so the Coriolis parameter at the origin is fo = 4 x 10-5 s-1 :. The planetary β parameter is β = 2 x 10-11 (ms)-1. The spatial resolution was tested by performing additional simulations with 257 X 257 gridpoints and verifying that similar results were also obtained. The timestep is 12 min, and the horizontal eddy viscosity is AH=104m2s-1 for all cases.
3.1 Vortex trajectory without topography
Before showing the trajectories of vortices on a β plane with variable topography, a standard example of a barotropic vortex only influenced by the planetary β effect is presented (i. e. on a flat bottom). This is shown in Figure 3a, where the trajectory of a cyclonic vortex is drawn every 12 h during 3 days; the numerically calculated vorticity contours at t=36 h are shown in panel (b). The vortex speed is approximately cβ˜10.5 km/h. This problem has been extensively studied by several authors, analytically and numerically, for atmospheric and oceanic vortices (see e. g. Fiorino and Elsberry, 1989; Mc Williams and Flierl, 1979). The important point to recall here is the formation of the so-called β-gyres (Figure 3b) due to the cyclonic motion and to potential vorticity conservation, which are responsible for the observed vorticity redistribution. Basically, the negative (positive) relative vorticity produced at the northeastern (southwestern) part of the cyclone induces the vortex to drift in the northwest direction. A complete description of the vortex trajectory , however, is very complicated. For instance, the precise direction of the initial trajectory depends on several factors, such as the vortex structure (size and strenght), and the β parameter. Furthermore, for these parameters the vortex drift can change dramatically after several days. This is due, in part, to the Rossby wave radiation, which directly interacts with the vortex structure. In order to clearly understand the influence of the topography on the initial vortex motion the numerical simulations in the following subsections are focused on periods of 3 days. Within this time-span, the vortex motion keeps an almost straight, northwestward trajectory.
Vortex trajectories for different latitudes
A set of 9 simulations on a β plane with variable topography has been performed, in which the same cyclonic vortex is initialized at 9 different positions (see Figure 1). The initial vortex positions are given in Table 2. For clarity, the results are analyzed separately in three groups of vortices each with the same initial latitude. Thus, vortices of simulations 1, 2 and 3 start at 12.5° N, cases 4, 5 and 6 are initialized at 15° N, and simulations 7, 8 and 9 start at 17.5° N. The general features of the vortex trajectories observed in the three groups are described here, and a more detailed discussion of the physical mechanisms is presented in subsequent sections.
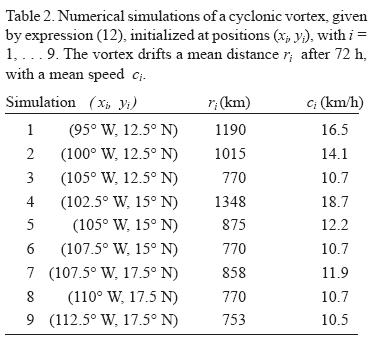
The vortex trajectories for latitude 12.5° N are shown in Figure 4, where the vortex center is indicated every 12 hours, and up to three days. The corresponding northwestward trajectory on the purely β plane (shown in Figure 3a) is also included. Obviously, the vortex motion in the absence of topography is identical for the three cases. A visible effect when the topography is included in the simulations is that cyclones 1 and 2 are forced to drift a larger distance than in cases without topography. On average, these vortices travel about 450 and 250 km more, respectively, when the topography is present than in the purely β plane. This is also shown in Table 2, where an approximate value of the traveled distance and of the mean speed is estimated for each simulation. Vortices 1 and 2 are clearly influenced by the continental topography due to their relative vicinity of it. For instance, vortex 1 is approximately at 370 km (3.7R) from the coast. Vortex 3, in contrast, is initially located at 550 km (5 5R), and drifts a similar distance as in the purely β plane case. This indicates that the topography plays a less important role on its increased speed (see subsection 3.3).
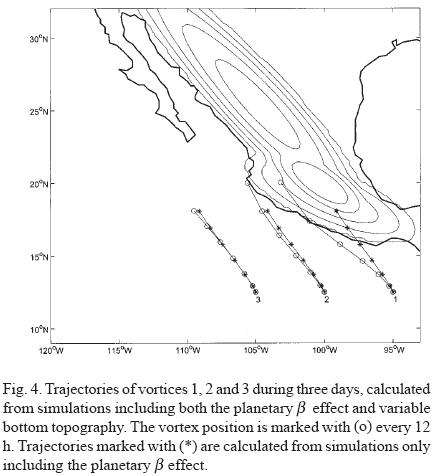
There are also important differences in the direction of the trajectories of these three examples. Clearly, vortex 1 is deflected more to the west, whilst vortex 3 keeps almost the same path as in the purely planetary drift. An evident reason for this is the orientation of the SMS, which is the closer topographic feature to this group of vortices. Because of its initial position, vortex 1 encounters the SMS, which acts as a barrier, forcing the cyclone to move more to the west. In contrast, vortex 3 is able to maintain its northwestward path, experiencing only a weak influence of the far topography. An intermediate case is vortex 2, which is also deflected to the west, although less dramatically than vortex 1. This is apparently because the cyclone does not get as close to the coast as vortex 1. Besides, as vortex 2 moves further north, the influence of the SMS becomes weaker, and the presence of the SMO (with a different orientation) starts to dominate.
Figure 5 shows the corresponding trajectories of vortices initiated at latitude 15° N. As in the previous figure, the three cyclones drift faster than in the case with no topography (see Table 2). The increased speed is much stronger for vortex 4 (closer to the continent) and weaker for vortices 5 and 6. Regarding the direction of the trajectories, vortices 4 and 5 have an additional component towards the continent as they move northwestward. Apparently, this is the typical "attraction" of the vortex towards the large scale topography, shown by Zehnder (1993) and described in ZS02. In particular, vortex 4 moves very fast towards the SMO, reaching the coast in almost 2.5 days. Vortex 5 moves somewhat slower and approaches over Baja California Sur in 3 days (recall, however, that the Peninsula is "flat" in these simulations). Since vortex 6 is far from the topography it is only slightly accelerated in the original northwest direction. It is worth noting that the attraction towards the continent is in contrast with the westward deflection observed in vortex 1 (previous figure). Basically, the SMS deflects the trajectory of that vortex to the left because this topographic feature is obstructing its northwestward motion, and the vortex is not able to climb it. In contrast, the orientation of the SMO does not obstruct the vortex trajectory. Instead, the purely topographic β effect associated with this orientation induces cyclone 4 to move further to the northwest. When the planetary β effect is added, the vortex gets closer to the continent.
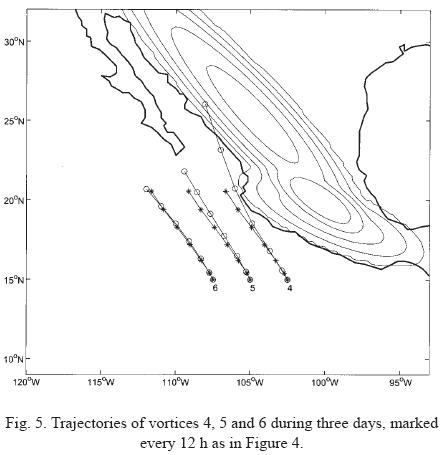
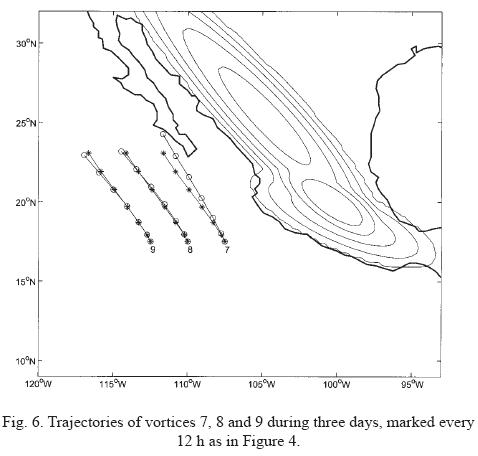
Trajectories of vortices initiated at a latitude 17.5° N are presented in Figure 6. The attraction of vortex 7 towards the continent is similar to that shown in previous figure. This can be attributed mainly to the SMO: as the cyclone drifts northward, the influence of the SMS becomes less important, whilst the influence of the SMO increases. Also, notice that the vortex moves faster when initialized closer to the coast; in contrast, vortices 8 and 9 nearly escape from the influence of the continental topography.
3.3 Increase of vortex speed
A remarkable influence of the topography on the vortex behaviour is the increase of the northwestward translation speed with respect to the case of the purely planetary β drift. This can be appreciated from most of the vortex trajectories in previous figures and in Table 2. Such behaviour can be attributed to the combination of the planetary and topographic β effects, which favors the northwestward motion. Indeed, for the present topographic orientation, the local "northwest" direction associated with the ascending slope of either the SMO and the SMS, points towards the geographic northwest direction (recall that the uphill direction corresponds with the local "north", see e.g. Zavala Sansón and van Heijst, 2000).
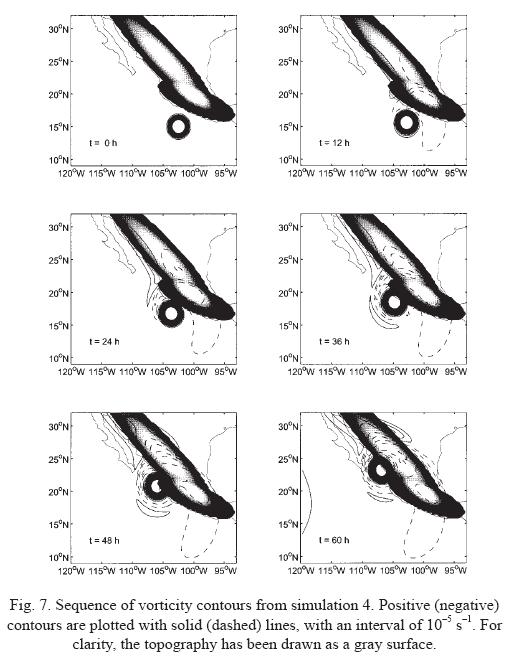
In order to study the vortex structure as it is forced to speed up, Figure 7 shows the calculated vorticity contours in simulation 4 during 60 h. This case is examined because the vortex travels about 450 km more than in the situation without topography during the same period of time (see Figure 5). Several important aspects can be observed from these plots. First, note the development of cyclonic, positive vorticity at the western part of the SMO at t=12 h; anticyclonic vorticity is also produced over the SMO and SMS. Both situations are due to stretching and squeezing effects due to the vortex circulation: fluid on top of the topography moves downhill, which induces the production of positive relative vorticity, while uphill motion implies squeezing of fluid columns which in turn acquire negative relative vorticity. The important point to stress here is that the anticyclonic vorticity over the topography reinforces the northwestward motion of the original cyclone along the coast. The mean speed of the vortex in this case is about 70% more than in the purely planetary β case (see Table 2). It must be emphasized, therefore, that the sum of the anticyclonic circulation induced by the topography and the planetary β gyres, is the physical mechanism associated with the increased speed of the vortex.
It is important to recall that even in the absence of the planetary β effect, a large-scale topography like the one used here induces a barotropic cyclone to drift. This was reported in the experiments and simulations on a f-plane by ZS02. This topographically-induced drift is shown in Figure 8a, where the trajectory of vortex 7 is plotted for the three cases: the purely topographic β, the purely planetary β, and the sum of both effects. The topographic β effect shows that the vortex is forced to move northward, although with a lower mean speed of approximately 3.6 km/h. As mentioned above, the case of the planetary β drift has a mean speed of Cβ ˜ 10.5 km/h. When both effects are added the vortex translation is reinforced in magnitude (C7 ˜ 11.9 km/h), and the resultant direction lies between the purely topographic and planetary trajectories. Vorticity contours calculated from a simulation with purely topographic effects at t =36 h are shown in Figure 8b. The negative relative vorticity induced over the SMO and SMS is evident, although weaker than in Figure 7. As a result, the vortex drifts at a much slower speed, than in the case of the combined β effects.
3.4 The topography as a barrier
In subsection 3.2 it was noted that the northwestward trajectory of vortex 1 (initially at 12.5° N, 95° W), is deflected towards the west due to the SMS. A similar situation occurs, although less dramatically, for vortex 2. This indicates that vortices are not able to "climb" the continental topography, but rather that they tend to move parallel to it. Therefore, the orientation of the continental topography plays a very important role in the vortex trajectory. Figure 9a shows the corresponding trajectories of vortex 1 under the influence of the topographic and/or planetary β effects. In contrast with simulation 7 (where the vortex is mainly influenced by the SMO, see Figure 8), the purely topographic β effect due to the SMS forces vortex 1 to move westward at a mean speed of 1.6 km/h, approximately. When the planetary β effect is added, however, the cyclone rapidly approaches the continent, where the topographic effect becomes important, and thus induces the vortex to drift nearly parallel to the coast. Figure 9b shows the corresponding vorticity contours from the simulation with only topography effects at t =36 h.
4. Discussion
The interaction of a cyclonic vortex with an idealized bottom topography representing the Mexican continental orography (the SMO and SMS) has been described by means of a barotropic model. A series of numerical simulations are performed, in which the vortex is initialized at the eastern North Pacific with latitudes between 12.5 and 17.5° N. This configuration resembles the motion of tropical cyclones produced in that area. The basic hypothesis of this study is that topography modifies the northwestward planetary β drift of the vortices by means of the redistribution of relative vorticity, due to stretching mechanisms associated with the mountains. This idea has been examined before by Zehnder (1993) and Zehnder and Reeder (1997), and experimentally verified by ZS02. The approach of the present paper, therefore, is to isolate the dynamical mechanisms affecting the vortex motion in a very specific region where cyclones are frequently formed.
The Main results are the following:
• The combination of the planetary and topographic β effects produces an increased vortex speed along its northwestern trajectory. This behavior was observed in all studied cases where the vortex is close enough to the continent. Such an effect is due to the anticyclonic circulation produced over the mountains, which pairs the β gyres and thus reinforces the drift speed.
• The direction of the trajectory, in contrast, depends on the initial position of the vortex with respect to the topography, and on the initial latitude. For vortices produced at southeastern regions (e. g. Figure 4) it was found that the orientation of the SMS is fundamental for the direction of the vortex path. Initially the cyclone approaches the continent mainly due to the planetary β effect. Due to the presence of the SMS, however, its path is strongly deflected westward, moving almost parallel to the coast. Because of purely mechanical effects, therefore, it is concluded that the vortices in this area are not able to move inland, or to "climb" the SMS.
• Vortices initialized at higher latitudes (see e. g. Figures 5 and 6) might be attracted towards the continental topography of the SMO. This deviation has been experimentally studied in ZS02 (see also Zehnder, 1993). By observing the whole vortex motion (e. g. Figure 7), it can be concluded that vortices close to the continent tend to drift along the coast, trapped under the influence of the SMO.
In general, a northwestward motion is usually observed for most of the tropical cyclones registered in the eastern Pacific. Their trajectories, however, often have a stronger western component than those presented in this study. There might be several reasons for this, such as the lack of a background mean-flow advecting the cyclones in the present simulations. On the other hand, when vortices are intense and induce a significant wind velocity over the continent, the present results suggest that they might be more prone to be affected by the continental topography, and therefore, a large-scale flow would be less important. Consider, for instance, the trajectory of hurricane Pauline (1997) in Figure 10, which was formed around 94° W, 13° N.
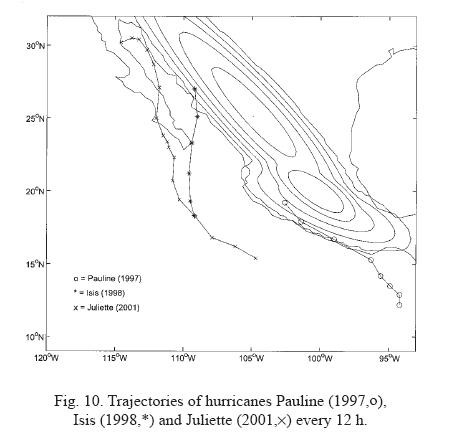
This vortex drifted almost parallel to the SMS, in a similar fashion as vortex 1 in Figure 4. Pauline also seems to show an increment on its drift speed when moving along the coastline, as reported here. It has also been observed that some intense vortices formed at northern regions (more than 15° N) tend to recurve their path and turn towards the continent. Such a behaviour is shown in Figure 10 for hurricanes Isis (1998) and Juliette (2001). These trajectories suggest that, as the vortices move towards higher latitudes, they approach the SMO and might get trapped by its influence (see e. g. Figure 6).
There are, of course, several cases of real tropical cyclones which have not followed the type of paths described in this study. It must be recalled that the present study deals with a strongly simplified model of cyclonic vortices affected by the Earth's rotation and by a very specific topographic feature, and therefore there is no intention to numerically reproduce historical tracks, nor to make predictions of vortex trajectories. The relevance of the present results (which are interpreted by exploiting the simplicity of the two-dimensional formulation) is that they give an indication on which vortices might be affected by large-scale topography, according to their position relative to the continent. A good understanding of the barotropic situation might also be important when using more sophisticated models, which are often difficult to interpret.
Using the present results as a starting point, there are at least two important issues that need further study: (i) Systematic, statistical studies of historical trajectories in the eastern North Pacific, together with the corresponding atmospheric and oceanic conditions. The aim could be to determine the possible importance of the mechanical effects considered in this study, or to discard them in cases where more evident physical mechanisms have a greater influence on the trajectory of the cyclones. (ii) An extended numerical study with barotropic vortices, in order to examine the role of the vortex parameters (strength, size), and topographic parameters (shape, height, orientation) in this area.
References
Adem, J., 1956. A series solution for the barotropic vorticity equation and its application in the study of atmospheric vortices. Tellus 8, 364-372. [ Links ]
Chan, J. C. L. and R. T. Williams, 1987. Analytical and numerical studies of the Beta-effect in tropical cyclone motion. Part I: Zero mean flow. J. Atmos. Sci., 44, 1257-1265. [ Links ]
DeMaria, M., 1985. Tropical cyclone motion in a nondivergent barotropic model. Mon. Wea. Rev. 113, 1199-1210. [ Links ]
Emanuel, K. A., 1999. Thermodynamic control of hurricane intensity. Nature 401, 665-669. [ Links ]
Fiorino, M. and R. L. Elsberry, 1989. Some aspects of vortex structure related to tropical cyclone motion. J. Atmos. Sci. 46, 975-990. [ Links ]
Holland, G. J., 1983. Tropical cyclone motion: Environmental interaction plus a beta effect. J. Atmos. Sci. 40, 328-341. [ Links ]
Kloosterziel, R. C. and G. J. F. van Heijst, 1992. The evolution of stable barotropic vortices in a rotating free-surface fluid. J. Fluid Mech, 239, 607-629. [ Links ]
McWilliams, J. C. and G. R. Flierl, 1979. On the evolution of isolated, nonlinear vortices. J. Phys. Oceanogr. 9, 1155-1182. [ Links ]
Pedlosky, J., 1987. Geophysical Fluid Dynamics, Springer-Verlag, 710 p. [ Links ]
Saffman, P. G. and Baker G. R., 1979. Vortex interactions. Ann. Rev. Fluid Mech. 11, 95-122. [ Links ]
Van Heijst, G. J. F., 1994. Topography effects on vortices in a rotating fluid. Meccanica 29, 431-451. [ Links ]
Zavala Sansón, L., G. J. F. van Heijst and J. J. J. Doorschot, 1999. Reflection of barotropic vortices from a step-like topography. Il Nuovo Cimento C 22, 909-929. [ Links ]
Zavala Sansón, L. and G. J. F. van Heijst, 2000. Interaction of barotropic vortices with coastal topographies: Laboratory experiments and numerical simulations. J. Phys. Oceanogr. 30, 2141-2162. [ Links ]
Zavala Sansón, L. 2002. Vortex-ridge interaction in a rotating fluid. Dyn. Atmos. Oceans 35, 299-325. [ Links ]
Zehnder, J. A. 1 993. The influence of large-scale topography on barotropic vortex motion. J. Atmos. Sci. 50, 2519-2532. [ Links ]
Zehnder, J. A. and M. J. Reeder, 1997. A numerical study of barotropic vortex motion near a large-scale mountain range with application to the motion of tropical cyclones approaching the Sierra Madre. Meteorol. Atmos. Phys. 64, 1-19. [ Links ]














