Introducción
Este estudio contiene dos demostraciones. Primero, que además de describirse, los resultados electorales pueden predecirse geográficamente. Segundo, que la estadística espacial tiene importantes aplicaciones en el área de los estudios electorales. Consecuentemente, en teoría este estudio confirma que la geografía es importante para el caso (O’Loughlin, 2002), y afirma que la geografía electoral mexicana, aunque incipiente, cuenta con un gran potencial teórico para los estudios electorales, particularmente por su situación de democracia emergente.
La realización de estas demostraciones reviste gran importancia para dos públicos en particular. Por un lado para los geógrafos políticos, quienes pueden ver con alivio que se responde en forma afirmativa a la pregunta que se plantea en el título de este estudio.1 Por el otro lado para los politólogos mexicanos, que confiadamente podrán analizar y considerar en sus análisis empíricos la importancia de los contextos geográficos en la determinación de los resultados electorales, al menos cuando se hable de resultados agregados geográficamente. La trascendencia de la geografía o el estudio de agregados humanos en unidades geográficas dentro de los estudios electorales deriva precisamente de la enorme ayuda que ofrece en la determinación de las razones “agregadas”, espaciales y temporales, que explican y predicen las victorias electorales. Esto lo logra porque analíticamente supone que las preferencias electorales de los individuos en un lugar no son independientes una de la otra, sino que están parcialmente correlacionadas. Las elecciones se ganan por mayorías, y no todos los partidos compiten con la misma fuerza en todos los lugares, por lo que resulta necesario ganar o en muchos lugares o en ciertos lugares que son clave por su número de votantes. Un análisis que utiliza solamente información individual de los votantes y no toma en cuenta los patrones de la autocorrelación geográfica y temporal del voto, sólo puede llegar a adivinar los resultados de una elección por simple azar.
Las dos demostraciones que contiene este estudio se construyen sobre tres tesis geográficas relativas a la Ciudad de México y que son las siguientes: 1) en la Ciudad de México son bajos los niveles de marginación y altos los niveles de segregación espacial socioeconómica, 2)presenta una marcada geografía del voto, y 3) la misma se halla más dividida geográficamente en su voto que en su ingreso (Vilalta, 2007a).2
El análisis espacial realizado aquí ratifica las tres tesis anteriores y agrega las dos siguientes: 1) que en la Ciudad de México la Alianza por el Cambio (APC)3 y el Partido de la Revolución Democrática (PRD) se excluyen geográficamente, y 2) sus resultados fueron altamente dependientes de la segregación espacial socioeconómica en la ciudad, si bien la Alianza es más espacialmente dependiente que el PRD.4 La implicación de estos hallazgos para futuras elecciones es que si la división entre ricos y pobres en la Ciudad de México aumenta, y en consecuencia también lo hace la segregación espacial socioeconómica, esto tendrá el efecto de dividir geográficamente aun más a la ciudad en sus preferencias partidistas.
Conceptual y metodológicamente hablando, los conceptos geográficos de cluster y outlier espaciales, así como las técnicas de estadística espacial que utilizamos en este trabajo, derivan de ideas originales traducidas en axiomas geográficos que han sido explicados a pro-fundidad en otros trabajos ya clásicos (Anselin, 1995; Tobler, 1970). Y aunque las aplicaciones aquí presentadas son novedosas dentro de la geografía electoral, sus proposiciones son factuales y sus formulaciones fácilmente comprobables.5
Además de la presente introducción, el estudio se ha ordenado en cuatro partes. La primera se divide en dos secciones: una consiste en una revisión de estudios previos sobre la geografía electoral mexicana, y la otra en una revisión de estudios sobre la segregación espacial y la marginación. La segunda parte detalla la metodología del estudio. La tercera parte muestra los resultados de los análisis, y contiene tres secciones, las cuales presentan los cálculos y mapas de la geografía del voto, de la segregación espacial socioeconómica, y finalmente la predicción geográfica de los resultados electorales. La cuarta parte se destina a la discusión y las conclusiones del estudio. Al final se incluye la bibliografía consultada.
Estudios previos
Esta parte se divide en dos secciones. En la primera se presenta un resumen de los estudios previos sobre la geografía electoral mexicana. La segunda sección se refiere a los estudios sobre segregación espacial socioeconómica también en México.
Sobre la geografía electoral mexicana y sus orígenes teóricos
El objetivo y la aportación de la geografía electoral mexicana han consistido en realizar una detección sistemática de los espacios y contextos regionales y locales favorables o desfavorables para los partidos en competencia. Cabe mencionar que esto ocurre en una etapa emergente de elecciones multipartidistas. En esta área de las ciencias sociales las teorías y las tendencias metodológicas estadounidenses han logrado un efecto significativo,6 lo cual se debe en buena medida a que algunos estudiantes mexicanos acuden a las universidades estadounidenses y al regresar traen consigo ciertos conocimientos y técnicas de investigación que son de uso común en ese país.7
La geografía electoral mexicana no tiene la tradición de otras ciencias sociales en el país. Hace sólo 40 años que con el uso de datos agregados y con carácter estatal se analizó y demostró la correlación que existe entre los diversos indicadores de modernización y los resultados electorales (Reyna, 1967). Desde entonces, y muy en particular desde finales de los ochenta, la literatura nacional especializada ha venido desarrollándose conforme a estándares científicos más que suficientes, y recientemente ha empezado a mostrar su propia revolución cuantitativa.8
Es interesante que con casi cuatro décadas de estudios la capacidad explicativa y el potencial predictivo de la geografía electoral no hayan sido cuestionados en los gremios de politólogos y geógrafos mexicanos,9 pues no hay estudios científicos en el país que la pongan a prueba o que por lo menos cuestionen una posibilidad al respecto, aunque fuera rutinaria u ocasional, a diferencia de lo que ha sucedido en otros países, principalmente Estados Unidos e Inglaterra, en donde los argumentos geográficos han sido cuestionados rigurosamente dentro de los estudios electorales (Flint, 2000; King, 1996).
Una razón posible de esta aceptación o ausencia de cuestionamientos en el ámbito electoral geográfico es la escasez misma de estudios de geografía electoral en el país; no se puede rechazar lo que escasea. Una buena noticia es que han aumentado las posibilidades de desarrollo de la geografía electoral nacional como consecuencia de la creciente compilación de datos fácilmente disponibles y organizados temporal y geográficamente. Asimismo, y en relación con lo anterior, ha habido un progresivo aumento de estudios electorales empíricos que utilizan una variedad de modelos estadísticos, que van desde los más simples pero suficientemente informativos, hasta otros más novedosos y específicos para el análisis geográfico y espacial.10
Los estudios previos que hemos revisado muestran un uso exclusivo y por ende una total dependencia de la teoría de la modernización (Deutsch, 1961; Huntington, 1991); todos dependen, y quizás sin saberlo los mismos autores, de la teoría de la estructuración (Giddens, 1990).11 Por un lado, la teoría de la modernización aplicada a la geografía electoral parte de la premisa de que el “lugar” o “contexto local” es una variable útil para explicar el comportamiento electoral en las sociedades tradicionales, pero no en las modernas. Por el otro lado, la teoría de la estructuración aplicada a la geografía electoral conecta el contexto local con el comportamiento individual.
Por ejemplo, dos efectos muy importantes de la modernización sobre el espacio social son el desarrollo de las comunicaciones y la urbanización. El primero hipotéticamente reduce la separación entre los individuos y estandariza el comportamiento sociopolítico; también hipotéticamente minimiza la relación afectiva del individuo con el lugar: vive en un lugar y piensa en otro u otros. Al respecto Meyrowitz y Maguire (1993) comentan que los medios de comunicación electrónicos han separado el “lugar social” del “lugar físico”; dicen por ejemplo que los medios de comunicación masivos en Estados Unidos han ocasionado una reducción en la diversidad de las experiencias personales, los comportamientos, las actitudes, las perspectivas y las expectativas de la sociedad estadounidense.
En cuanto a la urbanización, Deutsch (citado por Dietz y Shidlo, 1998) argumenta que las ciudades están más politizadas que las áreas rurales debido a que los residentes de las áreas urbanas están expuestos a más estímulos políticos, tales como los que emergen de los partidos políticos, sindicatos, movimientos sociales, medios masivos de comunicación, etc. (Deutsch, 1961). En el mismo sentido Huntington (1991) argumenta que conforme avanza la urbanización se politizan las necesidades sociales y se vuelven temas de debate.
Por otra parte, la teoría de la estructuración sugiere que tanto la agencia como la estructura humanas se afectan mutuamente. Por un lado la agencia es influida por “tradiciones, instituciones, códigos morales y maneras establecidas de hacer las cosas” (Giddens y Pierson, 1998: 77 ); por el otro, los individuos transforman las estructuras al ignorarlas, sustituirlas o reproducirlas de manera diferente a través de tiempo y del espacio. Esto implica que, como decía Durkheim (citado por Parkes y Thrift, 1980), no es posible separar el cambio social del espacio y del tiempo en donde se desarrolla; la sociedad, el espacio y el tiempo se complementan. Lo anterior ha motivado una variedad de estudios dirigidos a comprender precisamente “el efecto que tienen las características de las unidades geográficas donde los individuos residen en su comportamiento” (Books y Prisby, 1991: 38 ). Lo que más llama la atención respecto de esta revisión de estudios previos en el país es que pese a sus perspectivas teóricas tan claramente distinguibles, pocos mencionan que hacen uso de la teoría de la modernización y casi ninguno se refiere a su uso de la teoría de la estructuración.
Dados sus antecedentes modernistas, en la geografía electoral mexicana es posible ver el amplio uso de variables descriptivas de la modernización y por ende de la urbanización y la industrialización. Este uso de la modernización es múltiple, pero en esencia repetitivo si se observa al detalle. Cabe agregar que en el balance estas variables han mostrado ser efectivamente capaces de explicar las variaciones geográficas en los resultados electorales de México en los distritos electorales, municipios, ciudades, sistemas de ciudades y entidades federativas (véase el cuadro 1). Los resultados de los partidos políticos que con más frecuencia se han analizado son los del Partido Revolucionario Institucional (PRI), el Partido Acción Nacional (pan) y el Partido de la Revolución Democrática (PRD).12
CUADRO 1 Resumen de estudios previos sobre la geografía electoral de México*
| Autor y año | Unidad de análisis, Variable elección y periodo de estudio a | Variable predictiva | Medición | Efecto para el partido político a |
| Reyna (1967) | Estados (N = 32) | Urbanización | % > 2 500 habs. | PRI (-) |
| Presidente 1958 | Industrialización | % Trabs. manuales/no manuales | PRI (-) | |
| % Trabs. en manuf. | PRI (-) | |||
| % Trabs. agricultura | PRI (+) | |||
| Alfabetismo | % > 15 años analf. | PRI (-) | ||
| Ames (1970) | Estados (N = 32) | Urbanización | % > 2 500 habs. | PRI (-) |
| Presidente y Congreso 1952-1967 | Modernización | % Población benef. de progs. De agua potable | PRI (-) | |
| Reyna (1971) | Estados (N = 32) | Urbanización | % > 2 500 habs. | No PRI(+) |
| Presidente y Congreso 1952-1967 | Industrialización | % Trabs. en manuf. | No PRI(+) | |
| Tradicionalismo | % Pob. indígena | PRI (+) | ||
| Alfabetismo | % > 6 años alfabetas | No PRI(+) | ||
| Ingreso | Ingreso per cápita | No PRI(+) | ||
| Clase social | % Gerentes y profs. | No PRI(+) | ||
| % Vend. y admón. | No PRI(+) | |||
| % Trabs. industria | No PRI(+) | |||
| % Trabs. agricultura | No PRI(+) | |||
| Walton y Swen (1971) | Municipios (N = 318) | Urbanización | % Urbano | PRI (-) |
| Presidente y Congreso 1961-1967 | Industrialización | Cons. de electricidad | PRI (-) | |
| Valor prod. industria | PRI (-) | |||
| % Trabs. no agrícolas | PRI (-) | |||
| % Trabs. no manual | PRI (-) | |||
| % Trabs. prof. y tec. | PRI (-) | |||
| Ramos (1985) | Estados (N = 32) | Industrialización | % Trabs. industria | No PRI(+) |
| Presidente | Urbanización | % > 20 000 habs. | No PRI(+) | |
| 1964-1982 | Ingreso | Ingreso medio famil. | No PRI(+) | |
| Alfabetismo | % > 10 años alfabetas | No PRI(+) | ||
| Pobreza | Marginalidad | No PRI(+) | ||
| Klesner (1987) | Estados (N = 32) | Urbanización | % > 5 000 habs. | PAN (+), PRI(-), Izq.(+)b |
| Congreso | % > 50 000 habs. | PAN (+), PRI(-), Izq.(+) | ||
| 1961-1982 | Fuerza de trabajo | Agricultura | PAN (-), PRI (+) | |
| Industria | PAN (-), PRI (+) | |||
| Servicios | PAN (-), PRI (+) | |||
| Clase social | Clase alta urbana | PAN (-), PRI (+) | ||
| Clase media urbana | PAN (-), PRI (+) | |||
| Clase baja urbana | PAN (-), PRI (+) | |||
| Clase baja rural | PAN (-), PRI (+) | |||
| Estados (N = 32) | Urbanizacion | % > 5 000 habs. | PAN (+), PRI(-), PSUM(+)d | |
| Presidente 1982 | % > 80 000 habs. | PAN (+), PRI(-), PSUM(n.s.) | ||
| en áreas metropolitanas | ||||
| Industrializacion | % Trabs. en manuf. | PAN (+), PRI(-), PSUM(n.s.) | ||
| Region | 7 regiones | Afecta a todos (+,-) | ||
| Molinar y Valdés (1987) | Ciudad de mexico | Edad | Años de edad | PAN (n.s.), PRI(+), PRD(-) |
| Congreso | Mujer | Sexo femenino | PRI (+) | |
| 1985 | Ocupacion | Amas de casa | PRI (+) | |
| Burócrata | PRI (+) | |||
| Estudiantes | No especificado | NO PRI (+) | ||
| Molinar y Weldon (1990) | Distritos electorales | Urbanizacion | % > 50 000 habs. | PAN (+) |
| (N=290) | Manufacturas | % Trabs. en manuf. | PAN (+) | |
| Presidente y Congreso 1979-1988 | Educación | % > 6 años alfabetas | PAN (+) | |
| Habla indígena | % Pob. indígena monolingüe | PRI (+) | ||
| Inmigrantes | % de otro estado | PRD (+) | ||
| Region | 5 regiones | Afecta a todos (+,-) | ||
| Butler, Pick, y Jones (1991)d | Estados (N = 32) | Urbanizacion | > 2 500 habs. | PAN (+), PRI (-) |
| Presidente | > 5 000 habs. | PAN (+), PRI (-) | ||
| 1988 | Ocupacion | Agricultura | PAN (-), PRI (+) | |
| Construcción | PAN (+), PRI (-) | |||
| Administración | PAN (+), PRI (-) | |||
| Servicios | PAN (+), PRI (-) | |||
| Otros | PAN (+), PRI (-) | |||
| Desempleo | PAN (+), PRI (-) | |||
| Educacion | Primaria | PRI (-) | ||
| Secundaria | PAN (+), PRI (-) | |||
| Superior | PAN (+), PRI (-) | |||
| Alfabetismo | PAN (+), PRI (-) | |||
| Ingreso | Bajo | PAN (+), PRI (-) | ||
| Medio | PAN (+), PRI (-) | |||
| Alto | PAN (+), PRI (-) | |||
| Religion | No católicos | PAN (-), PRI (+) | ||
| Poblacion | Tamaño poblacional | PRI (-), FND(+)C | ||
| Densidad poblacional | PRI (-), FND(+) | |||
| Proyección a 1985 | PAN (+), PRI (-) | |||
| Habla indígena | PAN (-), PRI (+) | |||
| Migracion | Emigración | PRI (-), FND(+) | ||
| Población nativa | PAN (-) | |||
| Vivienda | Cocina y cuarto | PRI (+) | ||
| Agua potable | PAN (+), PRI (-) | |||
| Electricidad | PAN (+), PRI (-) | |||
| Televisión | PAN (+), PRI (-) | |||
| Teléfonos | PAN (+), PRI (-) | |||
| Vehículos | PAN (+), PRI (-) | |||
| Consumo de gas | PAN (+), PRI (-) | |||
| familia | Niños deseados | PAN (-), PRI (+) | ||
| Embarazos fallidos | PAN (+), PRI (-) | |||
| Jamas casados | PAN (-) | |||
| Actualmente casados | PAN (-) | |||
| Uso de píldoras | PAN (+) | |||
| Turismo | No especificado | PAN (+) | ||
| Empresa | Numero/personas | Afecta a todos (+,-) | ||
| Region | 5 regiones | PAN (+), PRI (-), IZQ(-)b | ||
| Klesner (1993) | Distritos electorales | Industrializacion | % Trabs. Sect secund. | PAN (+), PRI (-), IZQ(-) |
| (N = 157, 184 y 287) | Urbanizacion | % > 20 000 habs. | PAN (+), PRI(-)IZQn.s.) | |
| Congreso | Sin educación | % Sin educación | PAN (+), PRI(-)IZQn.s.) | |
| 1967-1991 | Participacion | % Votos válidos | PAN (-), PRI(+)Izq(+-) | |
| Catolicismo | % Pob. católica | Pan (+)PRI (-)PRD (-) | ||
| Region | 4 regiones | Afecta a todos (+,-) | ||
| Peschard (1997) | Ciudad de México | Educacion | Años de estudios | PAN (+), PRI(-)PRD (n.s.) |
| Preelecciones | Ingreso | Salario mínimo | PAN (+), PRI(-)PRD (n.s.) | |
| 1988-1994 | Edad | Años de edad | PAN (-), PRI(+), PRD(-) | |
| Klesner (1998) | Municipios | Industrializacion | % Trabs. sect. secund. | PAN (+), PRI (-), IZQ(-)b |
| (N = 2 403) | Urbanizacion | % > 20 000 habs | PAN (+), PRI (-), IZQ(+) | |
| Congreso | Sin educación | % Sin educación | PAN (-), PRI (+), IZQ(n.s.) | |
| 1991-1997 | Participacion | % votos válidos | PAN (-), PRI (+), IZQ(+-) | |
| Catolicismo | % Pob. Católica | PAN (+), PRI(-)PRD (-) | ||
| Ingreso | Nivel de ingreso | PAN (+), PRI(-)PRD (-) | ||
| Educacion | Nivel de educación | PAN (+), PRI(-)PRD (+) | ||
| Ocupacion | Desempleados | PRD (+) | ||
| Burocratas | PRI(+) | |||
| Estudiantes | PRD (+) | |||
| Amas de casa | PRI(+) | |||
| Region | 5 regiones | Afecta a todos (+,-) | ||
| Vilalta (2004) | Ciudades | Poblacion | % > 100 000 habs | APC(n.s), ePRI (n.s.), PRD (+) |
| (N = 89) | Etnicidad | % Lengua indígena | APC(+), PRI (n.s.), PRD (-) | |
| Congreso | Migración | % De otro estado | APC(n.s), PRI (-), PRD (n.s) | |
| 1994-2000 | Ocupacion | % Trabs. manuf. | APC(+)PRI(n.s.) PRD (+) | |
| Alfabetismo | % > 15 años alfabetas | APC(+)PRI(n.s.) PRD (-) | ||
| Ingreso | % > 10 sal. mínimos | APC(+)PRI(n.s.) PRD (-) | ||
| Religion | % Católicos | APC(+)PRI(n.s.) PRD (+) | ||
| Difucion espacial | % Voto en ciudades vecinas en elecciones previas | No afecta a ninguno | ||
| Region | 5 regiones | Afecta a todos (+,-) | ||
| Vilalta (2006) | Ciudades | Poblacion | % > 100 000 habs. | APC(n.s.), ePRI(n.s.) PRD (n.s.) |
| (N = 89) | Etnicidad | % Lengua indígena | APC(+), PRI(n.s.) PRD (n.s.) | |
| Congreso | Migracion | % De otro estado | APC(n.s.), PRI(n.s.) PRD (n.s.) | |
| 2000 | Ocupacion | % Trabs. manuf. | APC(+), PRI(n.s.) PRD (-) | |
| Alfabetismo | % > 15 años alfabetas | APC(n.s.), PRI(n.s.) PRD (n.s.) | ||
| Ingreso | % > 10 sal. mínimos | APC(+), PRI(n.s.) PRD (-) | ||
| Religion | % Católicos | APC(n.s.), PRI(-) PRD (n.s.) | ||
| Region | 5 regiones | Afecta a todos (+,-) |
* Este resumen contiene algunos estudios que incorporan información agregada geográficamente e información de carácter individual; invariablemente se describen los efectos de ambos tipos de información.
a Se lee como una correlación.
b El autor decidió considerar dentro de este grupo a todos los partidos con una ideología de izquierda.
c Frente Democrático Nacional (FDN), antecesor del actual PRD.
d Partido Socialista Unificado de México (PSUM).
e APCSE refiere a la Alianza por el Cambio, la coalición del PAN y el PVEMEN esa elección.
Para describir y explicar los resultados electorales de estos partidos se han utilizado variables sociodemográficas y socioeconómicas.13 Las sociodemográficas fueron principalmente la educación y la religión.14 En cuanto a la educación, se encontró que los lugares con porcentajes altos de población y niveles altos de educación han tendido a favorecer al pan, a desfavorecer al PRI, y para el PRD la relación ha sido variable (Vilalta, 2004; Klesner, 1993 y 1998; Peschard, 1997; Molinar y Weldon, 1990; Ramos, 1985; Reyna, 1971). En cuanto a la religión, se ha encontrado que los lugares con porcentajes altos de población católica15 son favorables para el pan y desfavorables para el PRI y el PRD (Vilalta, 2004 y 2006; Klesner, 1993 y 1998), aunque para el PRD hay excepciones (Vilalta, 2004).16
Dentro de las variables socioeconómicas destacan el ingreso17 y la especialización económica. Se ha encontrado que los lugares con porcentajes altos de población de ingresos altos tienden a favorecer al pan y a desfavorecer al PRI y al PRD (Vilalta, 2004 y 2006; Klesner, 1998; Ramos, 1985; Reyna, 1971). En cuanto a la especialización económica se observa que los lugares con altos porcentajes de población ocupada en la industria o en las manufacturas han tendido históricamente a favorecer al pan y a desfavorecer al PRI y al PRD (Vilalta, 2004y 2006; Klesner, 1987, 1993 y 1998; Molinar y Weldon, 1990; Story, 1987; Ramos, 1985; Walton y Sween, 1971; Reyna, 1971).
Más allá de la composición sociodemográfica y socioeconómica de cada lugar, se ha detectado la operación de importantes efectos contextuales locales en los resultados electorales.18 Entre estos efectos se encuentran las ya clásicas variaciones regionales en el apoyo a los partidos no priistas y el efecto del tamaño poblacional y del nivel de urbanización. Por ejemplo, en términos regionales se ha encontrado que el pan tiende a ser favorecido sistemáticamente en las regiones norte y Bajío del país, el PRI recientemente en algunas zonas urbanas del norte, y el PRD en el sur y en la Ciudad de México (Vilalta, 2004 y 2006; Klesner, 1993 y 1998; Molinar y Weldon, 1990; Story, 1987).
El efecto del tamaño de población y del nivel de urbanización también es o ha sido importante para algunos partidos. Se ha encontrado que a mayor población o nivel de urbanización, mayor es el apoyo para el pan y para el PRD y menor para el PRI (Vilalta, 2004; Klesner, 1987, 1993 y 1998; Molinar y Weldon, 1990; Ramos, 1985; Story, 1985; Walton y Sween, 1971; Ames, 1970; Reyna, 1967).
En síntesis, la detección de espacios de apoyo o rechazo para diferentes partidos políticos por la geografía electoral mexicana han sido su objetivo y su aportación natural desde que se fundara en los años setenta. El campo de la geografía electoral no muestra un amplio despliegue de teorías sobre la relación entre las características de los lugares y sus resultados electorales. Esto se debe a la escasez misma de teorías en la geografía política que pudieran ser sensatamente aplicables al comportamiento electoral, y realmente independientes entre ellas y especialmente de la teoría de la modernización.19
Tal vez sin pretender crear una teoría unificadora en la geografía política quede claro que al menos en la geografía electoral existe la necesidad de contar con “descripciones compactas, indicaciones para explicaciones, y herramientas para trabajar mejor” (Jones, 1954: 1). Entre las teorías más interesantes para ser aplicadas en el campo de la geografía electoral estarían la globalización20 (Castells, 1996), la difusión espacial de la democracia y de los partidos políticos (Vilalta, 2004; O’Loughlin et al., 1998).21 Metodológicamente está pendiente la resolución de otros asuntos que ya se han advertido en las elecciones mexicanas, como la posible heterogeneidad espacial en los resultados electorales y las implicaciones estadísticas resultantes (Vilalta, 2006).
Sobre la segregación espacial y la marginación
El estudio de la segregación espacial en México es más reciente y se halla menos desarrollado que la geografía electoral. La segregación espacial se ha definido como la “ocupación del espacio por grupos diferentes […] no distribuidos homogéneamente, sino al contrario, tendiendo a agruparse de acuerdo a características comunes de estatus, origen étnico, etc.” (Machado, 2001: 5 ).
En esta área de estudio también encontramos dos tipos de variables y en correspondencia de segregación: la segregación sociodemográfica y la segregación socioeconómica.22 En cuanto al primer tipo de segregación, dos artículos mexicanos arbitrados se han enfocado expresa pero aisladamente en la edad y en la etnia. Por ejemplo, en cuanto a la edad se ha registrado para el caso de la ciudad de Toluca un claro patrón de división residencial entre la población adulta mayor y la de otras edades, con la tendencia de los mayores a residir en el centro de la ciudad (Garrocho y Campos, 2005).23 En cuanto a la etnia, también se han analizado espacialmente -o en relación a lugares- la desigualdad social y la presión cultural que ejerce sobre la población inmigrante indígena en la Ciudad de México la sociedad dominante (Oehmichen, 2001).
En los estudios sobre la segregación socioeconómica en México -y en algunos casos sobre otros países de Latinoamérica-, se encuentra que los patrones de progresiva desigualdad social se desarrollan en simultaneidad con la multiplicación de las comunidades cerradas y la autosegregación de los más pudientes (Svampa, 2004; Cabrales y Zamora, 2001; Schteingart, 2001).
Particularmente frecuente en esta área de estudios es el uso -directo o indirecto- de la teoría de la globalización (González, 2005; Roberts, 2005; Graizbord et al., 2003). Con base en esta teoría se explican el empeoramiento de los ingresos, el aumento en las diferencias salariales entre trabajadores calificados y no calificados, el incremento en el número de mujeres que participan en las actividades económicas, y en consecuencia los aumentos en la segregación socioespacial (González, 2005).
Cuando se revisan estudios sobre otros aspectos relacionados con la segregación socioeconómica -pero analizados aisladamente-, como la marginación, la marginalidad y la pobreza, se advierte que la producción científica mexicana es mucho más amplia y cabe decir que de gran calidad (Cortés, 1997 y 2002; Bolvitnik y Hernández, 1999; Székely, 1998; Levy, 1994; Hernández-Laos, 1990).24 Nótese que académicamente la marginación y la pobreza se definen de manera diferente (González, 2005) pero siempre precisa. Una definición precisa de la marginación la formula Cortés (2002), quien la presenta como un concepto que intenta dar cuenta de las diferencias en el acceso a los beneficios del desarrollo para la población. La marginación es conceptualmente próxima a la idea de segregación espacial, puesto que entiende el fenómeno de la exclusión social por medio de mediciones geográficas; es decir, la marginación habla de lugares más que de individuos (Cortés, 2002).25
En cuanto a la pobreza y su reflejo geográfico, nuevamente se reporta un incremento en la desigualdad de los ingresos entre ricos y pobres, y una creciente separación física. También se advierten la sub-urbanización de la pobreza y el creciente alejamiento de las fuentes de trabajo en las ciudades para la población pobre (Roberts, 2005; Graizbord et al., 2003).26
En resumen, todos los estudios previos presentan en forma recurrente similares preocupaciones en Latinoamérica durante las últimas décadas: altos niveles de pobreza, una creciente desigualdad entre ricos y pobres, y también una creciente segregación espacial de tipo socioeconómico. Estos hallazgos y preocupaciones invitan a poner a prueba la hipotética relación entre la segregación espacial y los resultados electorales.
Metodología
Con fundamento en las ideas y evidencias previas, la hipótesis central de este estudio es que los patrones y procesos de la segregación espacial socioeconómica pueden predecir los resultados de sus elecciones locales. En esta sección se explica cómo se puso a prueba esta hipótesis para posteriormente, en la parte de resultados, realizar la comprobación de la misma.
En este estudio se utilizan como unidad geográfica base las delegaciones políticas de la Ciudad de México (N = 16). Decidimos analizar las elecciones locales en la Ciudad de México en el año 2000 por tres razones: la primera es que se trata de una ciudad en donde se ha medido previamente la segregación socioespacial y se ha discutido al respecto; la segunda razón es que se encuentra altamente politizada, en el sentido de que los votantes cuentan con un nivel de información política superior al de otras ciudades del país; y la tercera razón es que tiene la presencia de los tres partidos políticos mayoritarios del país, a diferencia de otras ciudades en donde la competencia es muy baja o es de corte bipartidista.
Como variable dependiente (VD) se utilizan como información base los resultados de la elección para jefe de gobierno de la ciudad en el año 2000.27 Como variable independiente (vi) se utilizan como información base los niveles de segregación espacial en el año 2000 y el cambio en los niveles de segregación espacial entre los años 1995 y 2000. Sobre la información base de todas las variables se elaboran coeficientes estadísticos espaciales que posteriormente se convierten en mediciones relevantes para el análisis (véase el cuadro 2). Este procedimiento se explicará a continuación.
CUADRO 2 Descripción de las variables*
| Variable dependiente (VD) | Descripción | |
| Resultados electorales | Porcentaje del voto para la apc, priy prden las elecciones para jefe de gobierno (2000) | |
| Variables independientes (VI) | Descripción | Efecto esperado en la VD* |
| Segregación espacial | Coeficientes locales de autocorrección (cael) sobre los índices de marginación (2000) | APC(+),PRI(n.s.), PRD(+) |
| Cambio en la segregación espacial | Coeficientes locales de autocorrelación espacial (CAEL) sobre el cambio en los índices de marginación (1995-2000) | APC(+), PRI(n.s.), PRD(+) |
* El efecto se lee en el sentido de una correlación.
Fuente: Elaboración propia.
Los índices de marginación oficiales de 1995 y 2000 fueron elaborados con un número diferente de variables. En este estudio fue indispensable rehacer o recalcular los índices para hacerlos comparables entre ambas fechas y poder obtener una razón de cambio válida para el periodo.28 El recálculo siguió la misma metodología estadística diseñada por el Consejo Nacional de Población (Conapo), con la virtud de que los índices recalculados poseen el mismo tipo y número de variables para cada año y por lo tanto son comparables.
El índice de marginación es un factor de varias variables consideradas como medidas apropiadas para representar la marginación. Conviene aclarar que los índices para cada año utilizan un número de variables diferente (véase el cuadro 3), pero su elaboración sigue la misma metodología estadística: el análisis factorial. El hecho de que las variables contenidas en los factores sean diferentes para cada año provoca que los índices como tales no sean comparables. Para resolver el problema de que fueran comparables entre años se decidió elaborar nuevos índices (análogos) con base en las mismas variables disponibles para 1995 y 2000, siguiendo el mismo procedimiento estadístico de Conapo. De esta manera pudimos obtener índices análogos, los cuales cuentan con la ventaja de proveer en paralelo el mismo tipo de información y hacer posible la búsqueda de una correlación entre ambas fechas. Una vez halladas las mismas variables disponibles para cada año, que servirían como base para el cálculo de los índices de marginación, se procedió a compilar tal información con base en las fuentes de información disponibles, que se detallan en el cuadro 4.
CUADRO 3 Descripción de las variables utilizadas en el cómputo de los índices de marginación de Conapo y análogo
Fuente: Elaboración propia con base en información de Conapo, 1995 y 2000.
CUADRO 4. Variables y fuentes de información del índice de marginación análogo
| Índice de marginación | Índice de marginación análogo (1995) análogo (2000) | |
| Porcentaje de población de 15 años o más analfabeta. | Conteo de Población, INEGI(1995) | Censo de Población, INEGI (2000) |
| Porcentaje de población de 15 años o más sin primaria completa. | Censo de Población, INEGI(1990) | Censo de Población, INEGI (2000) |
| Porcentaje de ocupantes en viviendas particulares sin agua entubada. | Conteo de Población, INEGI (1995) | Censo de Población, INEGI (2000) |
| Porcentaje de ocupantes en viviendas particulares sin drenaje ni servicio sanitario exclusivo. | Conteo de Población, INEGI (1995) | Censo de Población, INEGI (2000) |
| Porcentaje de ocupantes en viviendas particulares con piso de tierra. | Conteo de Población, INEGI (1995) | Censo de Población, INEGI (2000) |
| Porcentaje de ocupantes en viviendas particulares sin energía eléctrica. | Conteo de Población, INEGI (1995) | Censo de Población, INEGI (2000) |
| Porcentaje de población ocupada con ingresos de hasta dos salarios mínimos. | Censo de Población, INEGI (1990) | Censo de Población, INEGI (2000) |
Fuente: Elaboración propia.
No fue posible construir un índice de marginación análogo para el año 2005 y contar así con una observación más reciente y con una serie de tiempo de tres momentos. Las razones fueron dos y están relacionadas entre ellas. La primera es que el Conteo 2005 no contiene información sobre los ingresos de la población. La segunda es que para incluir tal variable en el índice se habría tenido que utilizar la información respectiva del censo del año 2000, por lo que la información necesaria para el cálculo de los factores de 2000 y 2005 habría tenido correspondencias de datos entre ambos años. Por consiguiente, tales factores o índices no habrían sido independientes, lo que anulaba la posibilidad de realizar comparaciones.
Se utilizan dos técnicas de estadística espacial y otra de estadística paramétrica común.29 Las técnicas y el orden en que se aplican son: 1)el coeficiente I de autocorrelación espacial global (CAEG), 2) los coeficientes I de autocorrelación espacial locales (CAEL), y 3) el análisis de regresión lineal simple (OLS). La primera técnica ya ha sido probada y comentada en México en estudios previos de geografía electoral (Vilalta, 2004 y 2006) y de economía regional (Vilalta, 2003). La segunda, pese a su alta utilidad analítica no parece haber sido aplicada en estudios previos en México.30 Las principales características de estos coeficientes locales son su novedad en la literatura científica y su comparativa robustez frente al coeficiente global de autocorrelación.31 La tercera técnica es de uso amplio en las ciencias sociales.
Aunadas a las tres técnicas estadísticas previamente mencionadas, se incorporan al estudio dos categorías espaciales que tampoco han sido utilizadas en estudios previos en México, pero que indudablemente son de fundamental importancia en cualquier análisis espacial: el cluster y el outlier espaciales.32 El cluster espacial puede definirse como un lugar o conjunto de lugares significativamente distinguibles por su relativa concentración de características similares y su relativa cercanía física. El outlier espacial puede definirse como un lugar o conjunto de lugares significativamente distinguibles por su relativa concentración de características diferentes de las de sus lugares vecinos en términos de cercanía física. En términos electorales y para efectos de este estudio, un cluster electoral sería una delegación o un conjunto de delegaciones con resultados electorales similares, y un outlier electoral sería una delegación o un conjunto de delegaciones con resultados electorales diferentes de los de sus vecinos.
El coeficiente I de autocorrelación espacial global (CAEG) permite detectar patrones geográficos generales dentro de un conjunto de datos. La fórmula es la siguiente (Moran, 1950):
En esta fórmula N significa el número de las unidades geográficas (delegaciones) en el mapa, w (i,j) es la matriz de distancias que define si las delegaciones i y j son o no vecinas geográficamente, y S 0 se formula de la siguiente manera:
El diseño de este coeficiente es similar al del coeficiente de correlación de Pearson. Sus valores varían entre +1 y -1, en donde el primer valor significa una autocorrelación positiva perfecta (perfecta concentración), y el segundo una autocorrelación negativa perfecta (perfecta dispersión); el cero significa un patrón espacial totalmente aleatorio.
Los coeficientes I de autocorrelación espacial locales (CAEL) permiten detectar los clusters y outliers espaciales.33 La fórmula es la siguiente (Anselin, 1995):34
En donde S 2 se obtiene de la siguiente manera:
El procedimiento que se sigue para probar la hipótesis de este estudio consta de cuatro pasos. El primer paso consiste en realizar el recálculo de los índices de marginación de cada delegación de la Ciudad de México y su cambio para el periodo 1995-2000. Esto nos permite contar con datos comparables.
El segundo paso consiste en calcular los coeficientes de autocorrelación espacial global (CAEG) para los resultados electorales para jefe de gobierno en 2000, para los índices de marginación en 2000, y para el cambio en los índices de marginación entre 1995 y 2000. Esto nos lleva a conocer los niveles de concentración del voto y de la marginación o segregación espacial y sus cambios en la Ciudad de México durante el periodo de interés.
En el tercer paso se calculan los coeficientes de autocorrelación espacial locales (CAEl) también para los resultados electorales y los índices de marginación. Estos coeficientes nos permiten, primero: hacer la detección específica de las delegaciones tipo clusters y outliers espaciales, y segundo: utilizar estos mismos coeficientes como mediciones de la variable independiente -la segregación espacial- en la ecuación de regresión lineal.
Finalmente el cuarto paso consiste precisamente en el análisis de regresión lineal. Se ejecutan cuatro ecuaciones -sobre dos modelos diferentes para dos de los tres partidos políticos mayoritarios- en donde la variable dependiente la integran los coeficientes de autocorrelación espacial locales (CAEL) de los resultados electorales por delegación en las elecciones locales del año 2000. Como variable independiente se utilizan en un modelo los CAEL de los índices de marginación, y en el otro modelo el cambio en los mismos entre 1995 y 2000. Este último paso, como se presenta en la parte siguiente, es el que demuestra la utilidad de la segregación espacial para la predicción de los resultados electorales en la Ciudad de México. Conviene mencionar que aun con un tamaño de muestra -o universo en este caso- tan pequeño, que sólo incluye 16 delegaciones o unidades geográficas, son claramente visibles los patrones de comportamiento, además de que las pruebas de significancia mantienen su capacidad de detectar relaciones estadísticamente significativas. Lo anterior se debe precisamente a la marcada geografía del voto en la Ciudad de México.
Por último es pertinente aclarar que toda la información base de este estudio está disponible en los sitios de internet del Instituto Electoral del Distrito Federal (IEDF) y del Consejo Nacional de Población (Conapo).
Resultados
Esta parte del trabajo está dividida en tres secciones. En la primera sección se mide y luego se mapea la geografía del voto en la Ciudad de México. En la segunda sección primero se mapea y luego se mide la segregación espacial socioeconómica. Estas dos secciones proceden de manera inversa porque el cambio en los niveles de marginación en esta ciudad tiene un patrón espacial particular que limita la capacidad de medición precisa de los coeficientes globales de autocorrelación espacial (CAEG).35 En la tercera sección probamos la capacidad de la segregación espacial para predecir el voto en la Ciudad de México.
La geografía del voto en la Ciudad de México: clusters espaciales
En esta sección se miden estadísticamente y se muestran cartográficamente los patrones geográficos de apoyo y de rechazo para cada uno de los tres partidos mayoritarios en las elecciones para jefe de gobierno del Distrito Federal del año 2000. Compitieron por el gobierno de la ciudad un total de diez partidos, de los cuales, la Alianza por el Cambio (APC, alianza compuesta por el Partido Acción Nacional y el Partido Verde Ecologista de México), el Partido Revolucionario Institucional (PRI) y el Partido de la Revolución Democrática (PRD) fueron los mayoritarios; en total recibieron 91% de los votos.
El cuadro 5 muestra los resultados de la elección para cada partido por delegación. El PRD obtuvo la victoria en la ciudad con 34.5% del voto total, la APC alcanzó 33.4%, y el PRI se quedó atrás de ambos con 22.8%. Cuando revisamos el promedio del voto y la desviación estándar para el conjunto de las delegaciones observamos que las diferencias entre los partidos empiezan a ser de mayor magnitud, sobre todo para el PRD y la APC. Se advierte que para el PRI la dispersión es mínima, es decir, su voto tiende a ser uniforme en todas las delegaciones de la ciudad.
CUADRO 5 Elección para jefe de gobierno (2000): porcentaje del voto de los tres partidos mayoritarios*
| Delegación | APC | PRI | PRD |
| Álvaro Obregón | 36.1 | 23.1 | 30.8 |
| Azcapotzalco | 38.5 | 22.4 | 30.9 |
| Benito Juárez | 42.3 | 22.1 | 27.8 |
| Coyoacán | 33.9 | 21.3 | 36.0 |
| Cuajimalpa | 35.0 | 25.2 | 30.8 |
| Cuauhtémoc | 34.1 | 25.2 | 31.4 |
| Gustavo A. Madero | 35.1 | 22.1 | 33.5 |
| Iztacalco | 32.4 | 22.9 | 35.3 |
| Iztapalapa | 28.6 | 23.0 | 38.3 |
| La Magdalena Contreras | 31.0 | 23.0 | 35.4 |
| Miguel Hidalgo | 40.0 | 25.2 | 26.8 |
| Milpa Alta | 15.1 | 25.4 | 50.4 |
| Tláhuac | 24.3 | 23.9 | 41.2 |
| Tlalpan | 32.2 | 21.2 | 37.7 |
| Venustiano Carranza | 34.8 | 24.2 | 31.8 |
| Xochimilco | 26.4 | 20.2 | 43.7 |
| Distrito Federal | 33.4 | 22.8 | 34.5 |
| Promedio | 32.5 | 23.2 | 35.1 |
| Mediana | 34.0 | 23.0 | 34.4 |
| Desviación estándar | 6.4 | 1.5 | 6.0 |
* El promedio, mediana y desviación estándar son sobre los resultados de las dele gaciones. N = 16.
Fuente: IEDF, 2000 y cálculos propios.
El cuadro 6 muestra los coeficientes de autocorrelación global espacial (CAEG). Los coeficientes globales indican que el voto para la APC y el PRD está concentrado espacialmente; el correspondiente al PRD es el más concentrado (I = 0.575).36 El coeficiente global para el voto del PRI no tiene ninguna significancia estadística (p = 0.293), por lo que se concluye que no posee ningún patrón geográfico y por consiguiente ninguna relación de dependencia o causalidad espacial probable.37
CUADRO 6 Elección para jefe de gobierno (2000): coeficientes de autocorrelación espacial global (CAEG)*
| APC | PRI | PRD | |
| Coeficiente I= | 0.446 | 0.083 | 0.575 |
| Significancia | 0.000 | 0.293 | 0.000 |
* La definición de vecindad en la prueba es la de estricta contigüidad física entre las delegaciones. La significancia estadística es una prueba Z de dos colas sobre una distribución teóricamente normal.
Fuente: Elaborado con base en los datos del cuadro 1.
Pasando ahora al análisis espacial local, el cuadro 7 muestra los coeficientes I de autocorrelación espacial locales (CAEL) para cada una de las delegaciones, junto con la interpretación espacial del mismo. La interpretación consiste en saber si la delegación cuenta con delegaciones vecinas similares o diferentes en sus resultados electorales. Nótese que en este caso un CAEL estadísticamente significativo de signo positivo (+) indica una delegación similar a sus vecinas (cluster espacial) y un CAEL de signo negativo (-) indica una delegación diferente a sus vecinas (outlier espacial).
CUADRO 7 Elección para jefe de gobierno (2000): coeficientes de autocorrelación espacial locales (CAEL)*
| APC | PRI | PRD | ||||
| Delegación | CAEL | Interpretación | CAEL | Interpretación | CAEL | Interpretación |
| Álvaro Obregón | 0.289 | 0.03 | 0.328 | |||
| Azcapotzalco | 0.580 | -0.319 | 0.540 | |||
| Benito Juárez | 0.410 | -0.132 | 0.415 | |||
| Coyoacán | 0.022 | 0.954 | 0.013 | |||
| Cuajimalpa | 0.344 | 0.860 | 0.768 | |||
| Cuauhtémoc | 0.186 | 0.000 | 0.429 | |||
| Gustavo A. Madero | 0.213 | -0.345 | 0.170 | |||
| Iztacalco | -0.005 | -0.049 | -0.014 | |||
| Iztapalapa | 0.060 | 0.067 | 0.151 | |||
| La Magdalena Contreras | -0.061 | 0.062 | -0.007 | |||
| Miguel Hidalgo | 0.873 | 0.387 | 1.119 | |||
| Milpa Alta | (2,081) | Cluster | -1.305 | (2.481) | Cluster | |
| Tláhuac | 1.841 | -0.089 | 1.549 | |||
| Tlalpan | 0.028 | 0.449 | 0.302 | |||
| Venustiano Carranza | 0.078 | 0.110 | 0.160 | |||
| Xochimilco | 0.850 | 0.235 | 1.358 | |||
* Coeficientes significativos en paréntesis; el nivel de confianza es de 99%. No se incluyen en el cuadro los valores Z por razones de espacio.
** APC: Alianza por el Cambio formada por el Partido Acción Nacional y el Partido Verde Ecologista de México.
Fuente: Elaborado con base en los datos del cuadro 1.
De tales coeficientes se concluye que la APC y el PRD contaron al menos con un cluster espacial o una delegación que se hallaba significativamente por encima o por debajo del promedio de voto en la ciudad. La delegación Milpa Alta -al sur de la ciudad- es la que posee esta característica de cluster espacial para ambos partidos.
Para la APC la delegación Milpa Alta representa un cluster espacial de rechazo electoral. Es decir, los resultados para la APC van mejorando conforme se aleja de Milpa Alta. Para el PRD en cambio, Milpa Alta representa un cluster espacial de apoyo electoral; este apoyo va disminuyendo conforme se aleja de Milpa Alta. Al comparar la magnitud de los coeficientes de los dos partidos queda claro que aun en semejanza, es más un cluster de apoyo para el PRD (I i = 2.481) que un cluster de rechazo para la APC (I i = 2.081). Aquí queda cuantificada y demostrada estadísticamente la geografía de exclusión entre ambos partidos. El PRI tampoco muestra algún patrón específico geográfico local.
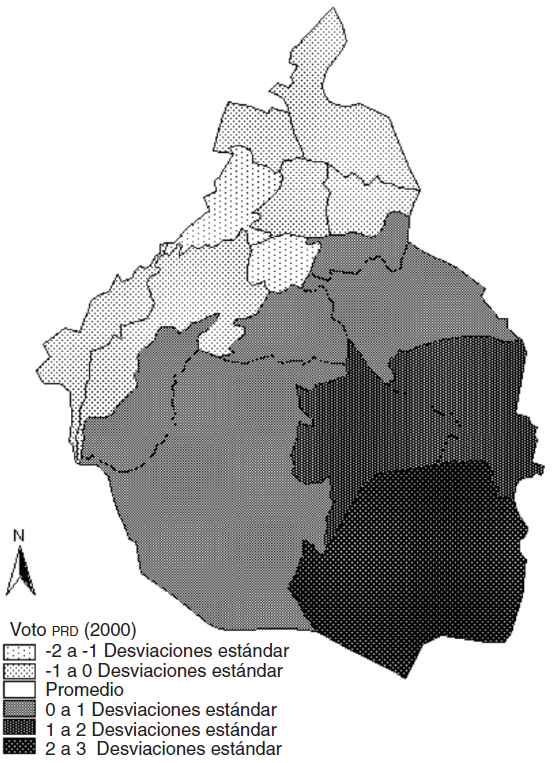
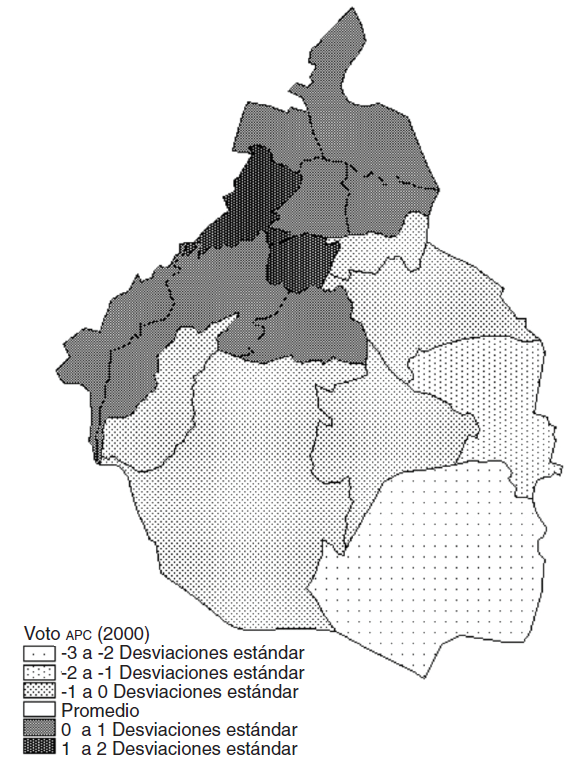
A continuación se presentan los mapas de los resultados electorales para la APC y el PRD (véase los mapas 1 y 2). Se observa gráficamente que el voto por la APC tuvo resultados mayores que el promedio -o se concentró- en las zonas norte y noroeste de la ciudad, mientras que el voto para el PRD fue mayor que el promedio en las zonas sur y sureste. En conclusión, las mediciones de los estadísticos espaciales y la representación gráfica de los mapas muestran la espacialidad del voto para la APC y el PRD y la exclusión geográfica entre ambos. 38 El caso del PRI es significativamente diferente del de los otros dos partidos, pues no muestra ningún patrón geográfico probable. Esto sugiere que su voto es aespacial, y que a diferencia de los otros, aquí no cabría ninguna explicación geográfica, al menos para esa elección en la Ciudad de México.39
FUENTE: Elaboracion propia con base en los datos del cuadro 5
Mapa 1. Voto por APC** *Se muestra el voto en desviaciones estándar **APC. Alianza por el Cambio formada por el Partido Accion Nacional y el Partido Verde Ecologista de Mèxico.
La segregación espacial socioeconómica: clusters y outliers espaciales
En la sección previa se comprobó que la APC y el PRD se excluyen geográficamente en la Ciudad de México. En esta sección se comprueba y mide ahora la segregación espacial socioeconómica que está presente en dicha ciudad.
El cuadro 8 muestra los índices de marginación oficiales no comparables y los índices ad hoc comparables de 1995 y 2000.40 Estos índices se utilizan como mediciones de segregación socioeconómica. Los cambios en los índices de marginación para el periodo 1995-2000 se muestran en el cuadro 9. Nótese que los índices oficiales de 1995 y 2000 contienen variables diferentes para cada año, por lo que la comparación es inválida. En cambio el índice recalculado contiene las mismas variables para 1995 y para 2000, por lo que la comparación entre ambos años es válida.
CUADRO 8 Índices de marginación (1995 y 2000)
| Delegacion | Indices de marginación oficiales (no comparables) | Ìndices de marginación recalculados (comparables) | ||
| 1995 | 2000 | 1995 | 2000 | |
| Álvaro Obregón | -1.656 | -1.873 | -0.003 | -1.106 |
| Azcapotzalco | -1.785 | -2.005 | -0.591 | -0.642 |
| Benito Juárez | -2.448 | -2.448 | -1.457 | -1.503 |
| Coyoacán | -2.102 | -2.190 | -0.825 | -0.858 |
| Cuajimalpa | -1.410 | -1.797 | 0.0679 | 0.313 |
| Cuauhtémoc | -2.005 | -2.090 | -0.838 | -0.717 |
| Gustavo A. Madero | -1.700 | -1.873 | -0.326 | -0.191 |
| Iztacalco | -1.709 | -1.930 | -0.497 | -0.440 |
| Iztapalapa | -1.447 | -1.726 | 0.327 | 0.302 |
| La Magdalena Contreras | -1.540 | -1.756 | 0.287 | 0.562 |
| Miguel Hidalgo | -2.004 | -2.136 | -0.849 | -0.871 |
| Milpa Alta | -0.913 | -1.305 | 2.745 | 2.747 |
| Tláhuac | -1.213 | -1.728 | 0.765 | 0.284 |
| Tlalpan | -1.672 | -1.884 | 0.344 | 0.540 |
| Venustiano Carranza | -1.750 | -1.938 | -0.640 | -0.573 |
| Xochimilco | -1.305 | 1.704 | 0.879 | 1.151 |
| Distrito Federal | - | |||
FUENTE: Elaboracion propia con base en la metodología de Conapo, 1995 y 2000 y datos disponibles para 1990, 1995 y 2000.
CUADRO 9 Cambio en los índices de marginación (∆ 1995-2000)
| Delegacion | Índices de marginación oficiles (no comparables)* | Índices de marginación recalculados (comparables)** |
| Álvaro Obregón | Disminuyó | Disminuyó |
| Azcapotzalco | Disminuyó | Disminuyó |
| Benito Juárez | Igual | Disminuyó |
| Coyoacán | Disminuyó | Disminuyó |
| Cuajimalpa | Disminuyó | Disminuyó |
| Cuauhtémoc | Disminuyó | Aumentó |
| Gustavo A. Madero | Disminuyó | Aumentó |
| Iztacalco | Disminuyó | Aumentó |
| Iztapalapa | Disminuyó | Disminuyó |
| La Magdalena Contreras | Disminuyó | Aumentó |
| Miguel Hidalgo | Disminuyó | Disminuyó |
| Milpa Alta | Disminuyó | Aumentó |
| Tláhuac | Disminuyó | Disminuyó |
| Tlalpan | Disminuyó | Disminuyó |
| Venustiano Carranza | Disminuyó | Aumentó |
| Xochimilco | Disminuyó | Aumentó |
| Distrito Federal | Disminuyó | Aumentó |
* Se destaca que los datos no son comparables válidamente.
** Comparación hecha con base en los datos del cuadro 4.
Fuente: Conapo, 1995 y 2000.
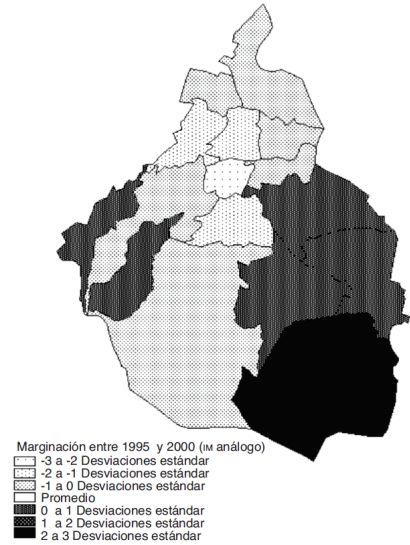
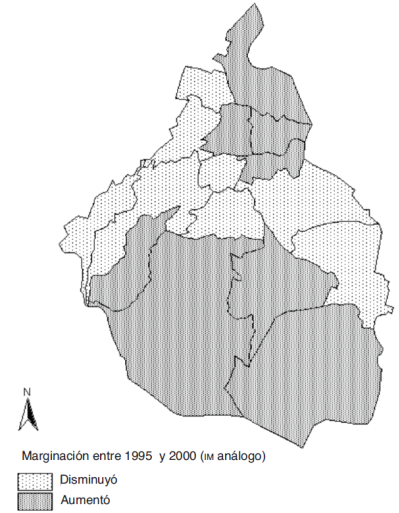
En números totales, la marginación aumentó en 8 delegaciones y disminuyó en las otras 8. Los dos mapas abajo presentan el cambio en la marginación en desviaciones estándar (véase los mapas 3 y 4). Geográficamente, el mapa 4 muestra que la marginación disminuyó en la parte central y aumentó en las zonas periféricas al norte y al sur de la ciudad.41
Pasando al análisis inferencial espacial, el cuadro 10 muestra los coeficientes de autocorrelación global (CAEG), los cuales nos llevan a tres conclusiones. Las dos primeras reflejan el fenómeno en estudio, y la tercera evidencia una limitación metodológica del CAEG.
CUADRO 10 Segregacion espacial socioeconómica: coefecientes de autocorrelacion espacil global (CAEG)*
| Indices de marginación recalculados (comparables) | |||
| 1995 | 2000 | ∆ 1995-2000 | |
| Coeficiente I= | 0.407 | 0.390 | 0.000 |
| Significancia * | 0.000 | 0.001 | 0.644 |
* La significancia estadística es una prueba Z de dos colas sobre una distribución teóricamente normal.
Fuente: Con base en los datos del cuadro 4. La definición de vecindad en la prueba es la de estricta contigüidad física entre las delegaciones.
La primera conclusión a que llegamos es que la segregación espacial en la Ciudad de México se mantuvo en niveles similares entre 1995 y 2000 (Vilalta, 2007 a ). La segunda es que estos coeficientes globales sobre la geografía de la marginación son menores en comparación con los coeficientes globales respectivos al voto para la APC y el PRD. Esto indica que la Ciudad de México está más dividida en lo electoral que en lo socioeconómico. La tercera conclusión es que el coeficiente global (CAEG), precisamente por ser global, es vulnerable a fallos en el registro de ciertos patrones geográficos.
Para explicar esto último conviene revisar de nuevo el mapa 4 y observar cómo se incrementa la marginación tanto en el norte como en el sur de la ciudad, y cómo disminuye en el centro, justamente dividiéndola en tres partes o franjas distintivas. Aunque efectivamente existió un patrón geográfico del cambio “centro frente a norte-sur”, éste no fue detectado por el coeficiente global (I = 0.000) a razón del arreglo espacial desconectado de la variable marginación. Esta desconexión física entre los dos grupos de delegaciones “aumenta o disminuye” ocasiona que el coeficiente global no pueda detectar ese patrón geográfico particular.
Los coeficientes de autocorrelación locales (CAEL) son insensibles a la circunstancia geográfica previa. El cuadro 11 muestra los coeficientes locales sobre los niveles de marginación en el año 2000 y sobre el cambio en los mismos entre 1995 y 2000.42
CUADRO 11 Segregación espacial socioeconómica: coeficientes de autocorrelación espacial local (CAEL)sobre el nivel de marginación (2000) y su cambio (∆ 1995-2000)
| Índices de marginación recalculados (comparables0029 | ||||
| Delegación | Coeficiente 2000 | Interpretación 2000 | Coeficiente ∆ 1995-2000 | Interpretación ∆ 1995-2000 |
| Álvaro Obregón | -0.057 | -0.002 | ||
| Azcapotzalco | 0.233 | -0.104 | ||
| Benito Juárez | 0.827** | Cluster | 0.001 | |
| Coyoacán | 0.134 | -0.051 | ||
| Cuajimalpa | -0.176 | 0.600* | Cluster | |
| Cuauhtémoc | 0.488 | 0.073 | ||
| Gustavo A. Madero | -0.047 | 0.162 | ||
| Iztacalco | 0.077 | 0.044 | ||
| Iztapalapa | -0.287 | 0.029 | ||
| La Magdalena Contreras | 0.047 | 0.338 | ||
| Miguel Hidalgo | 0.559 | 0.052 | ||
| Milpa Alta | 1.236** | Cluster | 0.000 | |
| Tláhuac | 0.898 | -1.045** | Outlier | |
| Tlalpan | 0.0329 | 0.426 | ||
| Venustiano Carranza | 0.041 | 0.185 | ||
| Xochimilco | 0.423 | -0.482 | ||
* p < .10; ** p < .05.
Fuente: Elaborado con base en los datos del cuadro 4 y sobre el cambio en los índices de marginación recalculados (comparables). definición de vecindad en la prueba es la de estricta contigüidad física entre las delegaciones.
Para el año 2000 destacan los resultados de una concentración -clustering- estadísticamente significativa de delegaciones con baja marginación alrededor de la delegación Benito Juárez, y de delegaciones con alta marginación alrededor de Milpa Alta, de mayor magnitud en esta última.
Sobre el cambio entre 1995 y 2000, destacan los resultados estadísticamente significativos de las delegaciones Cuajimalpa y Tláhuac. En el primer caso, la delegación Cuajimalpa es la central de un conjunto de delegaciones que redujeron en similitud con ella sus niveles de marginación durante ese periodo. Particularmente se trata de las delegaciones de Miguel Hidalgo y Álvaro Obregón, las cuales poseen de hecho niveles de marginación que están por debajo del promedio de la ciudad y van en progresivo descenso. La conclusión que arroja el CAEL es que Cuajimalpa es una especie de isla de baja marginación y en proceso de mejora en el interior de la Ciudad de México.
El caso de la delegación Tláhuac resulta llamativo geográficamente porque allí ocurre exactamente lo contrario a Cuajimalpa en su carácter de outlier espacial. Se trata de una delegación rodeada de otras cuya dinámica de marginación es diferente. Los niveles de marginación de Tláhuac están por encima del promedio de la ciudad, pero disminuyeron entre 1995 y 2000; lo que la hace espacialmente diferente es que dos de sus delegaciones vecinas, Xochimilco y Milpa Alta, tienen también niveles de marginación por encima del promedio, pero aumentaron o empeoraron entre 1995 y 2000. La delegación Iztapalapa también es vecina de Tláhuac y posee junto con ella niveles de marginación superiores y un proceso de disminución de los mismos. Sin embargo el efecto espacial de Xochimilco y Milpa Alta sobre Tláhuac es mayor, y es lo que la hace espacialmente diferente de sus tres delegaciones vecinas.
¿Se pueden predecir geográficamente los resultados electorales?
La pregunta que abre esta sección es central para la geografía electoral y la respuesta es afirmativa. Para responderla se utiliza como mecanismo geográfico causal la relación entre los niveles de segregación espacial y resultados electorales. Al poner a prueba el mecanismo se demuestra que tal relación es de una magnitud importante.43
En esta prueba se utilizan dos modelos de regresión para los dos partidos cuya distribución del voto poseía atributos de espacialidad: la APC y el PRD. En ambos modelos la variable dependiente (VD) son los coeficientes de autocorrelación locales (CAEL) en cada delegación sobre el voto para jefe de gobierno para la APC y el PRD en el año 2000.
En el primer modelo la variable independiente (VI) son los coeficientes de autocorrelación local de los índices de marginación recalculados para el año 2000 (CAEL-im00). O sea, mediciones de segregación espacial específicas para el año 2000. En el segundo modelo la variable independiente (VI) son los coeficientes de autocorrelación local (CAEl) de los índices de marginación recalculados para el cambio entre 1995 y 2000 (cael-Dim95-00). O sea, mediciones del cambio en la segregación espacial para el periodo 1995-2000. Ambas variables independientes representan mediciones de la segregación espacial en cada delegación respecto al promedio de la ciudad.
El cuadro 12 muestra los resultados del análisis de regresión. El primer modelo logra explicar casi 68% de la variación geográfica en el voto para la APC y 60% para el PRD. El segundo modelo logra explicar casi 38% de la variación geográfica del voto por la APC y 20% de la variación geográfica del PRD. Esto se debe a que el voto por el PRD dependió menos del cambio en los niveles de segregación que el voto por la APC.
CUADRO 12 Resultados de los modelos de regresión
| Modelo 1 | Modelo 2 | |||
| CAEL-APC | CAEL-PRD 2000 | CAEL-APC 2000 | CAEL-PRD 2000 | |
| CAEL-IM00a | 0.822*** | 0.777*** | - | - |
| CAEL-∆IM95-00a | - | - | -0.614** | -0.449* |
| Coeficiente de determinación (R2) | 0.676 | 0.604 | 0.377 | 0.202 |
| Anova (F) | 29.155*** | 21.377*** | 8.487** | 3.536* |
| Coeficiente Durbin -Watson (D-W) | 2.272 | 2.119 | 1.455 | 1.562 |
| Factor de inflación de varianza (VIF) | 1.000 | 1.000 | 1.000 | 1.000 |
a Coeficientes estandarizados (beta). Estas variables independientes son las mediciones de la segregación espacial.
* p < .10; ** p < .05; *** p < .01.
Nótese que los signos de los coeficientes en cada modelo son diferentes y que en el primero son de signo positivo. Para la APC el coeficiente estandarizado de signo positivo (B = 0.822) indica que su voto se concentra en las delegaciones que poseen bajos niveles de marginación. Para el PRD el coeficiente estandarizado de signo positivo en el primer modelo (B = 0.777) indica que su voto se concentra en las delegaciones que poseen altos niveles de marginación. Recuérdese que ambos partidos se excluyen geográficamente y que la marginación tiene efectos contrarios para cada uno. Pero al ser la VI una medición de la segregación espacial de la delegación y no el índice de marginación, el signo de esta relación para ambos partidos es positivo.44 En este sentido, la comparación de los resultados de cada ecuación para cada partido se debe enfocar en la magnitud del efecto y no en el signo del coeficiente.
En el segundo modelo los signos de los coeficientes estandarizados son negativos para ambos partidos. Para la APC el coeficiente estandarizado (B = -0.614) indica que donde menos cambian los niveles de segregación espacial, más se concentra espacialmente su voto. Lo mismo sucede para el PRD, aunque en menor magnitud (B = -0.449). Es decir, nuevamente la comparación indica que ambos partidos fueron más votados en las zonas en donde los cambios de los niveles de segregación socioeconómica resultaron más similares (clusters), ya fuera que subieran o bajaran, y la APC fue más dependiente de ello que el PRD. Esto puede significar que el PRD tiene un patrón geográfico del voto más estable, que su voto es más leal y menos dependiente del cambio en las circunstancias de infraestructura o del espacio construido en la Ciudad de México.
El primer modelo es, bajo cualquier estándar, altamente explicativo. El segundo modelo es aceptablemente explicativo.45 Algo importante que ambos modelos indican para ambos partidos es que la segregación espacial socioeconómica no solamente permite predecir su voto, sino que los beneficia en términos electorales. Comparativamente beneficia más a la APC que al PRD. Aunado a lo anterior y en terminología de geografía electoral, ambos modelos son indicativos de un efecto contextual local que opera en la Ciudad de México.46 Esto también sugeriría tentativamente la posibilidad de que hubiera un voto de clase social en la Ciudad de México, aunque se requerirían mayores pruebas al respecto.
Finalmente, ningún modelo parece adolecer de problemas de autocorrelación temporal en los residuales ni de multicolinealidad. No se incluyó al PRI en esta parte del análisis porque mostró ser un partido a espacial o sin una geografía del voto en la Ciudad de México para esta elección del año 2000.
Conclusiones
Este estudio evidencia dos cuestiones teórica y metodológicamente relevantes. Primero, que la geografía electoral influye en mucho más que lo indispensable, de ahí su importancia, y segundo, que la estadística espacial contribuye a aclarar tal importancia.47 Los estudios empíricos previos que se han realizado en el país confirman que la Ciudad de México está dividida electoralmente y segregada socioeconómicamente (Vilalta, 2007 a ).48
La demostración de la importancia de la geografía electoral se fundamenta en la prueba de que el voto y la segregación socioeconómica son espacialmente dependientes. El mecanismo causal geográfico opera en esta relación, ya que la segregación espacial socioeconómica tiene implicaciones electorales con base en el principio de que “donde un partido mejor refleje los intereses locales, ahí es donde recibirá el mayor apoyo” (Brustein, 1988: 71 ). Este principio se puede deducir de los hallazgos que han presentado los estudios previos de geografía electoral en México.49
En específico, la evidencia mostrada en este estudio confirma que tanto la APC como el PRD se excluyen geográficamente (Vilalta, 2007 a ). También se observa que el voto para el PRD está más concentrado geográficamente que el voto para la APC. Asimismo se prueba que ambos partidos dependen de la segregación socioeconómica de la población en la ciudad, pero que la APC es más dependiente de esto que el PRD.
Por ende, en caso de que esta dependencia se mantuviera constante se podría llegar a concluir que si aumentaran los niveles de segregación espacial socioeconómica en la ciudad, esto sería beneficioso para ambos partidos, y marcadamente para los partidos que conformaron en el año 2000 la APC.50 Más en concreto, en relación con los estudios previos y para efectos de predicciones electorales, si las diferencias de ingreso y la segregación espacial entre ricos y pobres siguiera aumentando conforme viene ocurriendo en las ciudades latinoamericanas (González, 2005; Roberts, 2005; Graizbord et al., 2003), y si esta alta dependencia entre segregación y resultados electorales se mantuviera constante, tanto la APC como el PRD dependerían fuertemente de la dinámica socioeconómica de la ciudad. Para el PRI todo lo anterior es irrelevante, puesto que su voto no sigue un patrón geográfico detectable en la Ciudad de México.51
La implicación social, riesgosa para los partidos políticos, de depender electoralmente de la segregación socioeconómica, es la tentación de caer en la promoción de campañas electorales que hagan un uso irresponsable de la confrontación de clases y la consecuente promoción del voto de clase social sobre cualquier otra alternativa. Este tipo de confrontación y discurso de clase social se presentó de hecho durante las elecciones presidenciales de 2006, y los conflictos políticos postelectorales fueron particularmente graves en la Ciudad de México.
Finalmente y en forma de nota metodológica cabe aclarar que la utilidad de la geografía y la estadística espacial para predecir el voto por la APC y el PRD y en este caso la inutilidad de predecir el voto por el PRI sugieren claramente la necesidad de incorporar en futuros estudios electorales dos tipos de información o unidades de análisis electoral: información individual e información agregada geográficamente.52 Con cuatro décadas y un número escaso de estudios en geografía electoral, y sin pretender ingenuamente buscar una teoría integral del comportamiento electoral en general, sigue siendo necesario que los estudios mexicanos ofrezcan respuestas demostrativas y ganen en ingenio y capacidad en la prueba de teorías formales.











 nueva página del texto (beta)
nueva página del texto (beta)