1.Introduction
De Young & Axford (1967) derived the so-called “plasmon” solution, which consists of the balance between the gas pressure within a decelerating (or accelerating) isothermal clump of gas and the ram-pressure of the environment into which it is travelling. This simple solution still continues to be used to model the dynamics of different astrophysical flows involving cometary clumps (see, e.g., Rivera-Oríz et al. 2019a, b; Veilleux et al. 1999; De Young 1997).
Modified versions of the plasmon solution of De Young & Axford (1967) have been obtained including the effects of:
the centrifugal pressure of the shocked environment (Cantó et al. 1998),
the self-gravity of the clump (Lora et al. 2015),
a clump with a polytropic equation of state (Cantó & Raga 1995),
entrainment of clump material by the streaming environment (Rivera-Ortíz et al. 2019a, b).
The formation of “tails” by wind/clump interactions was explored analytically by Dyson, Hartquist & Biro (1993).
Numerical simulations show that plasmon-style “interstellar bullet” flows are highly unstable, with rather intense fragmentation of the plasmon configuration (see, e.g., Klein et al. 2003; Raga et al. 2007). It can be argued that if a high speed flow rapidly disrupts a liquid droplet (see, e.g., Nicholls & Ranger 1969), a gas cloud would be disrupted with even greater ease.
On the other hand, it is clear that some astrophysical flows (e.g., the Orion “fingers” around the BN-KL object, see Rivera-Ortíz et al. 2019a) do show the characteristics predicted by the “braking plasmon” analytic model. In a recent series of papers, Pittard et al. (2009, 2010) and Goldsmith & Pittard (2017, 2019) show that clumps with high clump to environment density ratios can be substantially braked (or accelerated, depending on the reference system) before fragmenting and mixing with the environment. This “dense clump regime” was also explored by Rivera et al. (2019b), who carried out a comparison between an analytic plasmon model and numerical simulations. At least for such dense gas clumps, it appears that the plasmon model of De Young & Axford (1967) is still relevant.
In the present paper we consider the effect of the environmental gas pressure on the structure of a plasmon. This pressure will of course have an important effect for a plasmon moving at a relatively low Mach number (with respect to the environmental sound speed). Also, even in the case of a high Mach number plasmon, the environmental pressure will have an important effect in the plasmon “wings”, where the bow shock becomes highly oblique.
The paper is organized as follows. In § 2, we present the new plasmon model, and derive a full analytic solution for the shape of the plasmon. In § 3 we derive the equation of motion for the modified plasmon, and integrate it numerically to determine the velocity and position of the plasmon as a function of time. Finally, we present a discussion of the results in § 4.
2.The Plasmon Model
We consider the situation shown in the schematic diagram of Figure 1. In a cylindrical reference frame moving with the plasmon, the surrounding environment (of density
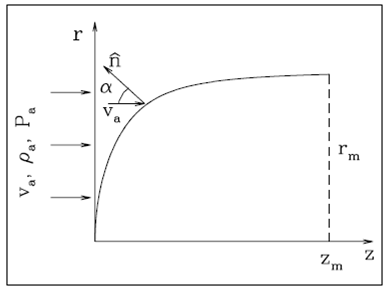
Fig. 1 Schematic diagram of a plasmon. In a frame of reference at rest with the plasmon, the environment (of density
In our model, we assume that the environment is isothermal, with a position-independent sound speed c a . We also assume that the plasmon is isothermal, but allow it to have a different sound speed c0. This choice is appropriate for a dense clump in an outflow from a young star, travelling within a higher temperature, neutral or partially ionized environment.
We assume that at any time in its evolution, the internal pressure stratification of the decelerating (or accelerating) plasmon instantaneously relaxes to the hydrostatic equilibrium, so that:
for an isothermal gas, where
with c0 being the isothermal sound speed and α the acceleration/deceleration of the plasmon. An exploration of the validity of equation 1 is presented in Appendix B.
As discussed in Appendix A, the pressure of the shocked environment in contact with the plasmon is approximately given by:
where
with
where M is the Mach number calculated with the velocity v a of the plasmon and the isothermal sound speed c a of the environment.
Now, setting
with β given by equation (5).
From the second equality of equation (6) we obtain:
with
It is clear that the plasmon solution ends at a finite zm, for which
In order to obtain the z(r) solution, we first consider the first equality of equation (6):
where ω is defined in equation (8). Also, from equation (7) we have:
Combining equations (10-11) we obtain the differential equation:
which can be integrated to obtain:
with ω given by equation (8). Equations (8) and (13) are then the solution for the shape of a plasmon interacting with an environment with a non-zero gas pressure.
This solution has the following limiting cases:
Equation (16) is the plasmon solution of De Young & Axford (1967).
In Figure 2, we plot the r(z) solutions (equations 8 and 13) for different values of β. It is clear that the length-to-width ratio of the plasmon grows as a function of decreasing β. This effect can be quantified by calculating the length-to-width ratio
where for the second equality, we have used the
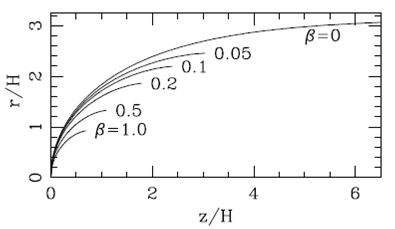
Fig. 2. The plasmon solution for different values of β. The curves are labeled with the corresponding β values.
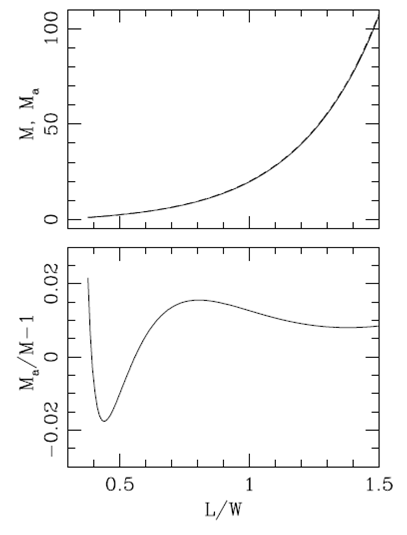
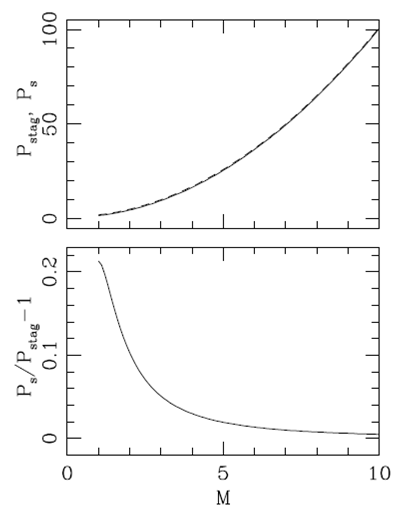
Fig. 3. Topplot: Mach numbers M (from the “exact” equation 17) and M a (from the approximate inversion 18) as a function of the length-to-width ratio of the plasmon. Bottom plot: relative error of the approximate inversion as a function of L/W.
It is of interest to have an analytic expression for calculating the Mach number M of the plasmon flow as a function of the observed L/W length-to-width ratio. As equation (17) does not have an analytic inversion, we propose the fit:
In Figure 3, we also show M
a
vs. M/L solution, as well as its relative deviation
Finally, we calculate the mass of the plasmon. To do this, we combine equations (1), (4) and (8) to obtain
with
with
We have not been able to carry out this integral analytically. However, in the limits of low and high β one obtains:
This latter, β >> 1, limit corresponds to a highly subsonic flow, for which our model is probably not appropriate.
A good analytic approximation for β in the full
with
Figure 4 (top) shows the dimensionless mass m obtained from a numerical integration of equation (21) as a function of β, as well as the analytic approximation m a . The bottom plot shows the relative deviation between these two solutions, and we can see that the approximate analytic solution has deviations of less that 3% relative to the exact (i.e., numerical) solution.
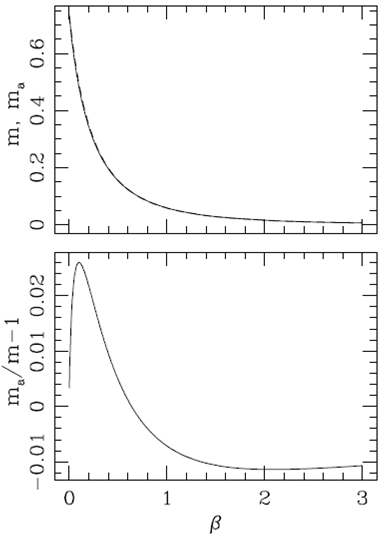
Fig. 4. Topplot: Dimensionless mass m (solid line, obtained from a numerical integration of equation 21) and the approximate solution m a (dashed line, from equation 24) as a function of β =1/M2 (where M is the Mach number of the flow). Bottom plot: relative error of the approximate, analytic solution as a function of β.
3.The Equation of Motion for the Plasmon
The plasmon’s equation of motion can be straightforwardly derived noting that the deceleration of the plasmon is
where we have also used equation (4). We note that in this equation,
Equation (26) was derived assuming that the plasmon has a time-independent mass. This is of course not necessarily true, since
the plasmon could evaporate from the back side (which is probably not an important effect in the pressure confined plasmon tail that we are modelling here),
the flow around the plasmon head could entrain a substantial amount of plasmon material.
A parametrization of the “detrainment” of material from a plasmon has been obtained by Rivera-Ortíz et al. (2019b) by comparing a mass-losing plasmon analytic model with numerical simulations. Through their combined analytic and numerical aproach, these authors estimate a characteristic timescale
for substantial mass loss from the plasmon. A mass conserving plasmon model is therefore appropriate only for evolutionary times
We first define dimensionless variables:
where x is the position of the plasmon, and
In terms of these dimensionless variables, equation (26) takes the form:
This is the equation of motion for the plasmon, and a numerical integration is presented in § 3.
For
(see equation 22 and 25) in the second equality of equation (30). With an initial condition (the initial Mach number of the plasmon), we integrate this equation to obtain:
It is clear that
We can integrate again to obtain the dimensionless position of the plasmon as a function of time:
where we have assumed that
In Figure 5 we present a comparison of the “large Mach number” analytical solution (equations 32 and 34) with a full, numerical integration of equation (30) for a plasmon with a
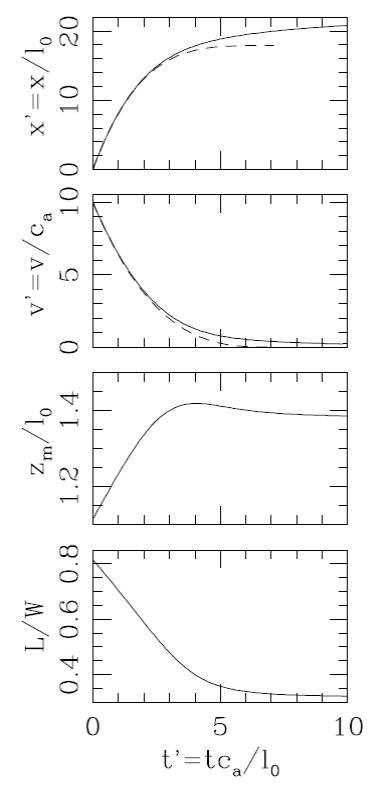
Fig. 5 Dimensionless position (top) and velocity (second from top) as a function of time. The solid curves correspond to the full (numerical solution of equation (30), and the dashed curves to the “high Mach number” analytic solution (equations 32 and 34). The two bottom frames show the dimensionless axial extent zm/l0 and the length-to-width ratio L/W of the plasmon as a function of time.
Figure 5 also shows the axial extent zm (equation 9) and the length-to-width ratio (L/W, given by equation 17) of the plasmon as a function of time. The length zm initially grows with time, reaches a peak (of ≈1.42l0) and then slowly decreases for times
4.Discussion
We have derived an analytic solution for the problem of an isothermal plasmon travelling supersonicaly within an environment with a non-zero pressure.
For a hypersonic flow with M >>1, our model coincides with the De Young & Axford (1967) plasmon solution.
Interestingly, we find that even for large values of M the non-zero environmental pressure produces a cut-off for the plasmon, which is terminated at the distance zm and cylindrical radius rm from the plasmon head given by equations (9) and (15). Thus cutoff results in rather stubby plasmons (see Figure 2), unless one goes to very high Mach number flows.
We find that the length-to-width ratio of the plasmon solution (equations 17 and 18) has values ranging from ≈0.4 to ≈1.5 for Mach numbers
We also integrated the equation of motion for the new plasmon solution, and for high Mach numbers we find (not surprisingly) a time-dependent position and velocity which are similar to the ones found from the De Young & Axford (1967) plasmon solution. When the flow reaches a Mach number of ≈3, the new solution starts to separate from the De Young & Axford model, with the plasmon slowing down more slowly, and never stopping completely (while the De Young & Axford plasmon stops at a finite distance along its direction of motion).
Finally, we would like to point out an important qualitative result obtained from our new model. The ratio between the extent along the symmetry axis of the plasmon zm and the scale-height H (equation 9) only has a logarithmic dependence on











 nueva página del texto (beta)
nueva página del texto (beta)