1. Introduction
Turbulent, collimated flows (plumes and jets) in stratified environments can be modeled in terms of radially averaged conservation equations, which are solved to obtain the flow properties as a function of position along the outflow axis. In their classical paper, Morton et al. (1956) derived the equations and proposed a parametrized form for the "entrainment velocity", with which environmental material is dragged into the collimated flow.
Morton et al. (1956) derived an analytic solution for a collimated, entraining, buoyant flow in the so-called "Boussinesq approximation". In this approximation, the effect of the compressibility of the flow was neglected, except in the "buoyancy term" which appears in the momentum equation.
In the astrophysical context, this kind of approach was first used by Bicknell (1984) to model extragalactic jets. An application of this kind of model to Herbig-Haro (HH) jets was presented by Raga et al. (1993).
For the case of HH jets, one can assume that the heating due to shocks and/or turbulent dissipation is balanced by the radiative cooling of the gas. Because of the steep rise of the cooling function of the ISM for temperatures above ≈ 103 K, the energy balance condition results in very similar temperatures regardless of the magnitude of the shock/turbulent heating. Therefore, the flow can be approximated as being approximately isothermal (see Raga et al. 1993).
As with the Boussinesq approximation (appropriate for almost incompressible flows), the assumption of an isothermal flow leads to a simplified set of conservation equations. These equations have an approximate analytic solution, valid for high Mach number jets embedded in exponentially stratified environments. These solutions are applicable for bipolar HH outflows at the outer edge of a molecular cloud (which can be modeled as having an exponential density/pressure stratification extending over a few pressure scale heights).
The paper is organized as follows. In § 2, we derive the model equations. An analytic solution of these equations is derived in § 3. In § 4, examples for different flow parameters (appropriate for HH jets) are presented. § 5 discusses in some detail the approximations that have been done in order to construct the model. Finally, the conclusions are presented in § 6.
2. The entraining jet model
In order to have a simple model leading to analytic results, we study a radially averaged turbulent jet model, in which the equations are closed by giving a recipe for an entrainment velocity The model is further simplified by assuming that both the jet and the surrounding environment are isothermal (though with different temperatures).
The isothermal approximation for an HH jet has been used, e.g., by Raga et al. (1993). The justification for this is that the turbulent dissipation produces an energy gain that is balanced by the rapidly rising ISM cooling function at ≈ 103K. The energy then always results in a temperature of this order, regardless of the precise value of the thermal energy source. We then model the jet as a. flow with a constant, co = 3 km s-1 isothermal sound speed. For the surrounding environment, we assume a temperature of ≈ 100 K, leading to a ca = 1 km s-1 isothermal sound speed. The energy equation of the flow in this way is replaced by the (much simpler) condition of isothermality.
We further assume lateral pressure balance between the jet and a hydrostatic the ambient medium:
where ρa is the (stratified) ambient density, ρ is the jet density (constant over the jet cross section because of the isothermal and pressure balance conditions) and Pa is the ambient pressure, which obeys the hydrostatic balance condition:
where g is the acceleration of gravity (with positive values of g corresponding to a gravitational force in the - z direction). For constant g this equation has the well-known integral:
Where P0 is the pressure at z = 0 and
We now write the continuity and the z-momentum equation for an axisymmetric flow:
where z is the axial coordinate, r the cylindrical radius, w the axial velocity, u the radial velocity, p the density, and P is the pressure.
As is usual for modelling turbulent jets or plumes (see, e.g., Hunt & van den Bremer 2011), we apply an operator
where we have also used equations (1) and (2), and assumed that the jet has a "top hat" axial velocity cross section (with an axial velocity w). These equations can straightforwardly be interpreted as the mass and momentum (non-) conservation of the gas flowing along the jet.
In order to close the system of equations (6-7) we use the simple "a-prescription":
with α ≈ 0.1, appropriate for a jet with Mach number M = w/ca > 1 (see Raga et al. 1993).
Expanding the derivatives of equations (6) and (7) and using conditions (1) and (2) we can obtain the differential equations:
where
M = w/ca is the (appropriately defined) Mach number of the jet, r is the outer radius of the jet cross section and H is the environmental pressure (and density) scale height (see equation 3).
Equations (9-10) can be integrated numerically in a straightforward way starting from the conditions M = M0 and r = r0 at z = 0. In the following section, we describe an approximate, analytic solution for this system of differential equations.
3. Approximate analytic solution
In order to proceed analytically, we carry on as follows. It is clear that for a highly supersonic jet (with M≫1, as appropriate for an HH jet) the second term on the right hand side of equation (9) is much smaller than the first term. This can be seen in more detail evaluating the two terms with the values of α, c0 and c given above, and assuming a jet with M ≈ 100, r ≈ 1015cm and an environment with H ≈ 1016cm. Also, from the scaling with M of the two terms on the right hand side of equation (10), we see that they dominate over the third term (inserting the parameters discussed above, one sees that the first two terms are actually comparable).
In this way, we derive the simplified system of equations:
This simplication is due to the simple fact that the buoyancy terms are negligible in a high Mach number flow.
Now, in order to obtain an analytic solution, equations (12-13) can be combined to obtain the differential equation:
with solution:
This result can then be inserted in equation (12) to obtain the differential equation for the Mach number:
with solution:
with
where for the second equality we have used the definition of β given by equation (11).
This result can now be inserted in equation (15) to obtain the jet radius as a. function of z:
Equations (17-19) are the full analytic solution for the propagation of a steady, entraining, isothermal, highly supersonic jet moving in the direction of decreasing pressure within an exponentially stratified hydrostatic environment.
The model can be straightforwarldy recalculated for the case in which the acceleration of gravity points in the +z direction (i.e., changing the sign of g in equation 7). The resulting solution is:
This is the solution for a jet moving into a hydrostatic environment in the direction of increasing pressures (which can be directly obtained from equations 17-19 with the substitution H → -H).
4. Numerical examples
Let us now consider a bipolar outflow embedded in an exponentially stratified environment with the outflow axis aligned with the pressure gradient. Given the parameters of the system, we can use equations (17-19) and equations (20-21) to compute the flow in the directions of decreasing and increasing ambient pressures (respectively).
For the environment, we assume an isothermal sound speed ca = 1 km s-1 and a pressure scale height H = 1016cm. For the jet we assume a c0 = 3 km s-1 sound speed, a w0 = 100 km s-1 initial velocity (corresponding to a M0 = w 0 /ca = 100 initial Mach number) and a r0 = 1015cm initial radius. We also assume that the "entrainment prescription" has α = 0.1 (see equation 8). These parameters have already been used in § 2 and § 3. With these parameters, from equation (18) we obtain κ = 0.36.
The results obtained for this value of κ (as well as for two bracketing values κ = 0.1 and κ = 1.0) are shown in Figure 1. In this Figure, for positive z we show the solution corresponding to decreasing ambient pressures equations (17-19) and for negative z the solutions corresponding to increasing ambient pressures equations (20-21).
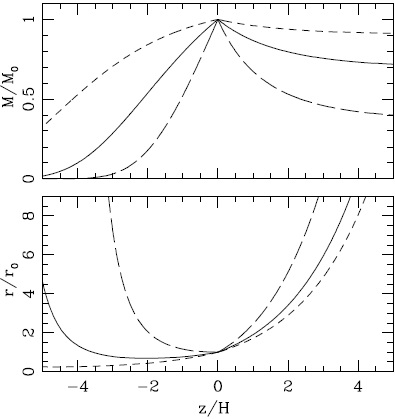
Fig. 1 Mach number (top) and jet radius (bottom) as a function of distance z from the source. The Mach number and the jet radius are adimensionalized with the corresponding ejection values, and the distance from the source is given in units of the environmental pressure scale height H. The exponential environmental stratification has pressures that decrease for positive z (and increase for negative z). The solid curves correspond to a model with the dimensionless parameter κ = 0.36 (see equation 18) deduced from the nominal HH jet parameters chosen in § 4. The short and long dash curves correspond to the two bracketing values κ = 0.1 and 1.0 (respectively).
In the top frame of Figure 1, we see that (as expected) a stronger slowing down of the outflow is obtained for the lobe in the region of increasing ambient pressures (i.e., for negative z). In the bottom frame of Figure 1 we see that for z > 0 the jet radius monotonically grows with z. For the κ = 0.1 and 0.36 solutions, for z < 0 the jet radius first decreases with increasing distances from the source (i.e., for more negative z-values) and then has a rapid rise at larger distances. In the k = 1.0 solution, the jet radius grows monotonically (for increasing distances from the source) in the z < 0 region. These behaviours can be understood from a visual analysis of equations (17-21).
A clear feature of the jet Mach number is that for z > 0 (i.e., in the direction of decreasing ambient pressure) it has a non-zero asymptotic limit for large distances from the source (see the top frame of Figure 1). From equation (17), it is clear that this asymptotic Mach number has a value:
Therefore, an evaluation of the k parameter (see equation 18) directly gives us an estimate (through equation 22) of whether or not entrainment will produce a substantial braking in a jet emerging from a stratified environmental structure.
For the case of an outflow travelling in the direction of increasing environmental pressure, the Mach number of the jet goes to zero in a rather drastic way (as an exponential of an exponential, see equation 20). For this outflow lobe one would expect a jet velocity that has a dramatic drop over distances corresponding to a few environmental scale heights.
5. Discussion
5.1 The effect of neglecting the buoyancy force
This paper discusses a simple steady, isothermal, entraining jet model. This problem has an analytic solution valid for high Mach number jets, in which the buoyancy force can be neglected. The magnitude of the errors introduced by neglecting the buoyancy can be evaluated as follows.
If we have a non-entraining, steady, isothermal jet, the flow along the axis obeys Bernoulli's theorem:
where c0 is the isothermal sound speed of the jet, w is the axial velocity, w0 is the ejection velocity, ρ is the density, and ρ0 the ejection density. Assuming lateral pressure balance (i.e., ρ/ ρ0 = Pa (z)/P0 where Pa (z) is given by equations 2-3), we then obtain the relation
where M = w/ca is the Mach number of the flow (relative to the environmental sound speed ca). We note that this equation can be obtained straightforwardly by setting α = 0 in equation (9).
Therefore, as expected, the effect of the buoyancy is to produce an encrease in the velocity (or Mach number) of a jet travelling in the direction of decreasing environmental pressure. For our example of a jet with an initial Mach number M0 = 100 and with c0 /ca = 3, this effect is quite small. Putting these numbers in equation (24), we see that for z = 10H. the jet Mach number has a value M10 ≈ 100.9, so that the resulting acceleration is indeed very small. Because of this, neglecting the buoyancy force does not introduce significant effects for jets of Mach number ≈ 100.
5.2. The assumption of lateral pressure balance
The assumption of lateral jet/environment pressure balance for modelling astrophysical jets in a stratified environment was first used by Icke (1991). It is, however, unclear that this is a valid approximation in the case of high Mach number flows, since they can develop relatively large pressure imbalances. These pressure imbalances lead to the formation of "crossing shocks", as shown by the steady simulations of jets in stratified environments of Falle & Wilson (1985) and Wilson & Falle (1985).
Canto & Raga (1996) carried out comparisons between steady jet simulations and analytic, lateral pressure balance models of jets travelling in an exponentially stratified environment. Interestingly, they find that even though the numerical simulations develop systems of crossing shocks (corresponding to local lateral pressure imbalances), the general properties of the flow (i.e., the jet velocity and trajectory) are in good agreement with the analytic, lateral pressure balance analytic model.
Therefore, we expect that the predictions from the models described in the present paper are likely to be at least a qualitatively correct description of the real flows.
5.3. The assumption of an outflow axis parallel to the pressure gradient
We have assumed that we have an outflow system with a jet/counterjet axis parallel to the direction of the environmental pressure gradient. If we have a jet in the outer edge of a molecular cloud (which could be modeled as having an exponential pressure stratification), this is indeed a very particular case!
For the general case of an outflow axis at an angle to the direction of the environmental gradient, a steady, non-entraining jet model predicts that the jet/counterjet system will curve in the direction of decreasing pressures (see Canto & Raga 1996).
However, as this deflection of the jet beam is due to the buoyancy force, in the case of high Mach number jets it occurs over distances of many scale heights (see Canto & Raga 1996). Therefore, for outflows propagating over distances of only a few environmental pressure heights we will have straight jets in which the entrainment produces the slowing down of the outflow velocity described by equations (17-21), but with an effective scale height Heff = H/cosφ (where H is the environmental pressure height and φ is the angle between the pressure gradient and the outflow axis).
5.4. The entrainment velocity parametrization
As described in § 2, it is necessary to adopt a "parametrization" for calculating the entrainment velocity (see equation 8). We have adopted the parametrization of Raga et al. (1993), which was based on the analysis of experimental results of Canto & Raga (1991). This parametrization is of course not unique (see Komissarov 1990, who adopted a somewhat different parametrization).
Experiments of subsonic jets in stratified environments (Kaminski et al. 2005) show that parametrizations of the entrainment velocity similar to the one of Raga et al. (1993) are also appropriate (at least in an approximate way) for this kind of flow. Adjustments to the entrainment velocity parametrization (in order to reproduce laboratory experiments of subsonic jets in stratified environments) have been proposed by van Reeuwijk et al. (2016).
As there are no published experimental results of supersonic jets in stratified environments (that we are aware of), we are forced to assume that in this case the entrainment velocity parametrizations for jets in uniform environments are still approximately applicable (as is the case for subsonic jets, see van Reeuwijk et al. 2016). Clearly, this parametrization is the primary source of uncertainties in the models that we are presenting.
6. Conclusions
This paper describes a simple, new analytic solution for the problem of an entraining jet in a stratified environment. This solution is an interesting addition to the modelling of turbulent jets and plumes, for which analytic solutions exist in some limiting cases, but which generally depends on numerical integrations of the conservation equations (see, e.g.. Hunt & van de Bremer 2010).
The model describes a jet/counterjet system embedded in an exponentially stratified, isothermal environment, which could correspond to the outer boundary of a molecular cloud. There are two solutions:
Jet travelling into regions of decreasing pressure: the entrainment of environmental material leads to a slowing down of the jet, which can be substantial provided that the dimensionless parameter k (see equation 18) is at least of order unity (see equation 22). Otherwise, the jet will emerge unscathed (i.e., with a velocity very similar to the ejection velocity) from the molecular cloud,
(Counter-) jet travelling into regions ofincreasing pressure: over a distance of a few environmental scale heights a substantial braking of the jet will take place, regardless of the parameters of the flow.
This is a very interesting prediction, which gives a clear framework for interpreting observations of bipolar HH jets, and can also serve as a guide for computing numerical simulations of HH jets in stratified environments (see, e.g., O'Neill et al. 2005).











 nueva página del texto (beta)
nueva página del texto (beta)


