ARTÍCULO ORIGINAL

 

Análisis estadístico para datos de conteo: aplicaciones para el uso de los servicios de salud

 

Statistical analysis for count data: use of healthcare services applications

 

 

Aarón Salinas-Rodríguez, M en C; Betty Manrique-Espinoza, M en C; Sandra G Sosa-Rubí, Dr en C

Centro de Investigación en Evaluación y Encuestas, Instituto Nacional de Salud Pública. Cuernavaca, Morelos, México

Solicitud de sobretiros

 

 

---

RESUMEN

OBJETIVO: Describir algunos de los modelos estadísticos para el estudio de variables expresadas como un conteo en el contexto del uso de los servicios de salud.
MATERIAL Y MÉTODOS: Con base en la Encuesta de Evaluación del Seguro Popular (2005-2006) se calculó el efecto del Seguro Popular sobre el número de consultas externas mediante el uso de los modelos de regresión Poisson, binomial negativo, binomial negativo cero-inflado y Hurdle binomial negativo. Se utilizó el criterio de información de Akaike (AIC) para definir el mejor modelo.
RESULTADOS: La mejor opción estadística para el análisis del uso de los servicios de salud resultó ser el modelo Hurdle, de acuerdo con sus presuposiciones y el valor del AIC.
DISCUSIÓN: La modelación de variables de conteo requiere el empleo de modelos que incluyan una medición de la dispersión. Ante la presencia de exceso de ceros, el modelo Hurdle es una opción apropiada.

Palabras clave: variables de conteo; uso de servicios de salud; modelos de regresión; estadística; México

---

ABSTRACT

OBJECTIVE: To describe some of the statistical models for the study of count variables in the context of the use of health services.
MATERIAL AND METHODS: We used the Seguro Popular Evaluation Survey to estimate the effect of Seguro Popular on the frequency of use of outpatient health services, using Poisson regression models and negative binomial, zero-inflated negative binomial and the hurdle negative binomial models. We used the Akaike Information Criterion (AIC) to define the best model.
RESULTS: Results show that the best statistical approach to model the use of health services is the hurdle model, taking into account both the main theoretical assumptions and the statistical results of the AIC.
DISCUSSION: The modelling of count data requires the application of statistical models to model data dispersion; in the presence of an excess of zeros, the hurdle model is an appropriate statistical option.

Key words: health services; statistical models; statistics; Mexico

---

 

 

El uso y análisis de variables que se expresan en la forma de un conteo (variable con un valor entero no negativo, y = 0,1,...) es frecuente en el ámbito de la salud pública. Esto es en particular cierto para el caso específico del uso de servicios de salud, en los cuales y para el contexto específico de los modelos de regresión, en muchos de los análisis se utiliza como variable de respuesta una variable de conteo; pueden mencionarse los siguientes: el número de visitas al médico (algunas veces desagregadas por especialidad del médico),^1,2 el número de días de estancia hospitalaria,³ el número de fármacos prescritos,⁴ o el número de visitas a los servicios de emergencia,⁵ entre otros.

En general, un enfoque estándar para analizar variables de conteo es el modelo de regresión Poisson.^6,7 Sin embargo, son conocidas las limitaciones de este enfoque que se desprenden del supuesto restrictivo de que la media y la varianza para la distribución Poisson deben ser iguales.^6-8 Por esta razón se ha planteado en la literatura una serie de alternativas, incluidos el uso de la regresión binomial negativa,⁹ los modelos de clase latente⁵ o los modelos de ecuaciones estructurales.¹⁰

En este último sentido, el objetivo de este trabajo es describir algunas de las alternativas estadísticas disponibles para el análisis de las variables de conteo y comparar los distintos modelos expuestos para evidenciar sus ventajas y desventajas, todo ello en el contexto general del uso de los servicios de salud.

En la descripción que sigue se exponen los fundamentos de algunos de los modelos de regresión alternativos para variables de conteo y en seguida se ilustra su aplicación mediante el empleo de datos referentes a la utilización de servicios de salud en el contexto de la evaluación de impacto del Seguro Popular (SP). Es importante mencionar que, dado que el texto está dirigido a investigadores de la salud, el nivel de complejidad y notación técnica se mantendrá al mínimo para permitir al lector seguir la secuencia de la exposición; empero, donde sea necesario, se utilizan algunas expresiones o fórmulas y, de manera particular, notación matricial para denotar un vector de valores (para las variables independientes o los coeficientes de regresión) mediante el uso de símbolos con una raya inferior.

Modelos de regresión para datos de conteo

Regresión Poisson

Como se mencionó, el modelo de regresión común para datos de conteo es el de regresión Poisson. Este modelo se ha descrito ampliamente en la bibliografía estadística en general^6-8 y en textos específicos para datos de con-teo,^9,11 por lo que aquí sólo se enuncian sus principales características, así como su especificación dentro de una estructura de regresión y en términos de su función de verosimilitud.

Como cualquier modelo de regresión, el de regresión Poisson requiere una correcta especificación de la media condicional, es decir, que la distribución condicional para la variable de respuesta sea correctamente especificada así como el parámetro relacionado con su valor esperado. Para la regresión Poisson se asume que la distribución condicional de y_i dado x_i se distribuye como una variable aleatoria Poisson con función de densidad:

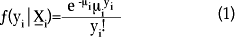
y el parámetro para la media condicional:

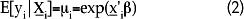
Si la especificación para la distribución condicional de la variable de respuesta, así como la de la media condicional, es correcta, y bajo el supuesto de que se tienen observaciones independientes, entonces se puede utilizar la siguiente función de log-verosimilitud para obtener estimadores consistentes de β:

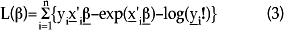
donde L(·) representa la función de log-verosimilitud.

Por lo regular, los paquetes estadísticos ofrecen estimadores de β que maximizan esta función. Sin embargo, y para obtener inferencias válidas respecto de β, todavía es necesario verificar el supuesto de que la media y varianza condicionales para este modelo son iguales. Se ha demostrado que, aunque este supuesto no se cumpla (lo cual sucede la mayor parte de las veces), el estimador puntual de β es aún válido, pero no así el estimador de su error estándar, y por tanto las inferencias respecto de β.^9,11

Por ello se han propuesto algunas alternativas que conservan el supuesto de una distribución condicional Poisson, pero que suavizan el supuesto de que la media y la varianza son iguales, esencialmente al ajustar los errores estándar ante la presencia de sobredispersión (que la varianza sea más grande que la media) o sub-dispersión (que la varianza sea más pequeña que la media). En particular se ha propuesto el uso de errores estándar robustos (algo también conocido como método de estimación de pseudomáxima verosimilitud)⁶ el empleo de un enfoque de quasiverosimilitud⁷ o la utilización de errores estándar bootstrap.¹²

Aun así, se han detallado bien las limitaciones del modelo de regresión Poisson, en particular para modelar datos relativos al uso de servicios de salud. Cameron y Trivedi¹¹ han mostrado que el modelo no es adecuado por lo siguiente: a) no se cumple el supuesto de equi-dispersión, debido sobre todo a la presencia de heterogeneidad no observada; b) existe un número excesivo de ceros, esto es, una frecuencia observada de ceros que no es consistente con el modelo Poisson; y c) hay mul-timodalidad, ya que si las observaciones se toman de distintas poblaciones, la distribución observada puede ser multimodal. Sin embargo, esto puede corregirse si el efecto de las covariables es el mismo para las distintas poblaciones.

Regresión binomial negativa

Una de las principales razones por las que el modelo Poisson falla es la heterogeneidad no observada. Esto significa que hay factores no observados, en especial características de los individuos, que ejercen alguna influencia sobre la variabilidad relacionada con la variable de respuesta.

El problema es que la heterogeneidad no observada puede tener algunas consecuencias para los procesos de inferencia estadística.^9,13 En primer término, puede introducir sobredispersión y, en segundo, un número excesivo de ceros. Esta heterogeneidad, ignorada por el modelo Poisson, puede modelarse de manera explícita mediante el uso de la regresión binomial negativa.^9,11

Existen al menos dos formas en las que la distribución binomial negativa puede derivarse;^7,9 la más común consiste en asumir que se está ante la presencia de una mezcla de distribuciones, en la cual los datos observados se distribuyen como una Poisson, pero se presupone un elemento de heterogeneidad individual no observado (que sigue una distribución gamma en su formulación clásica) que refleja el hecho de que la verdadera media no se ha medido perfectamente.⁹ La segunda asume que existe una forma particular de dependencia entre eventos, en el sentido de que la ocurrencia de un evento incrementa la probabilidad de ocurrencia de otros pos-teriores,¹¹ aunque esto último sólo puede dilucidarse en estudios longitudinales. Para fines de este artículo se utiliza la primera derivación.

La función de densidad para la distribución binomial negativa se determina por la siguiente expresión:

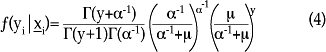
donde α es un parámetro de dispersión (α > 0) y Γ(·) es la función gamma. El parámetro de dispersión a es el que ayuda a definir la relación entre la media y la varianza condicionales, conocida en términos estadísticos como función varianza. Si, por ejemplo, α = 0, entonces la media y la varianza son iguales y se tiene el modelo Poisson. Por otro lado, las funciones más comunes para la relación media-varianza de la distribución binomial negativa son la lineal y la cuadrática.⁷

La función de log-verosimilitud para el modelo de regresión binomial negativa, con función de varianza cuadrática, después de alguna manipulación algebraica de la función de densidad, es la siguiente:

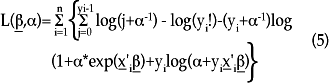
que es la utilizada por la paquetería estadística para encontrar los estimadores de β.

Regresión Poisson cero-inflado

Si bien es cierto que el modelo binomial negativo se ha desarrollado para modelar de modo explícito la heterogeneidad no observada, también es cierto que esa misma heterogeneidad es originada por un número excesivo de ceros. Es decir, observar más ceros que los que son consistentes con el modelo Poisson, cuestión que llega a ser común cuando se analizan datos relativos al uso de los servicios de salud, en especial para la utilización de los servicios hospitalarios.

De manera particular, es posible que el mecanismo aleatorio que dio origen a los datos de conteo muestre una mayor concentración para algún valor específico, que puede ser el cero (como ocurre con el uso de los servicios de salud) o cualquier otro valor positivo. Esto implica que dicho valor tiene una mayor probabilidad de ocurrencia que la especificada por la distribución Poisson o cualquier otra distribución.

Para el caso específico de los ceros -y en el contexto del uso de los servicios de salud- es posible que los ceros tengan un doble origen. Por ejemplo, si se pregunta ¿cuántas veces en los últimos 12 meses acudió a solicitar servicios de salud como paciente externo? Los ceros observados pueden ser originados porque la persona no utiliza los servicios de salud nunca o porque en esos 12 meses no utilizó los servicios de salud. Esto significa que se tiene una mezcla de distribuciones, por lo que no sería adecuado asumir en esta instancia que los ceros y no ceros se han generado por un mismo proceso.

En todo caso, si se tiene información respecto del origen de los ceros, se pueden estimar los parámetros relacionados con una distribución con valores concentrados en cero. De manera particular, los modelos para datos de conteo cero-inflado le confieren mayor peso a la probabilidad de que la variable de conteo sea igual a cero, al incorporar un mecanismo que divide a los sujetos con valor en cero, y cuya probabilidad es p(x_1iβ₁), e individuos con valor positivo y probabilidad 1 - p(x_1iβ₁). En consecuencia, la función de probabilidad para un modelo de regresión Poisson cero-inflado es una mezcla de un modelo Poisson estándar y una distribución con función de masa concentrada en cero.

De manera más formal, y de acuerdo con Lambert,¹⁴ el modelo de regresión Poisson cero-inflado puede especificarse como sigue. Primero se definen las siguientes cantidades Φ_i = Pr(y_i = 0) y μ_i = μ(x_i,β); la primer a cantidad es la probabilidad de que la variable de conteo sea igual a cero y, la segunda, el valor esperado cuando la variable de conteo asume un valor positivo.

En primera instancia, debe hallarse una manera estadística para expresar Φ_i, de tal modo que se obtengan sólo valores no negativos. Para esa razón, Lambert propuso una parametrización para Φ_i con base en la función logística y la ubicó en una estructura de regresión, de tal forma que un vector de covariables z_i podía utilizarse para modelarΦ_i, es decir:

En tal caso, y en términos de un modelo de regresión, el interés se centra en calcular (γ,β). Si se define de manera adicional una variable indicadora para denotar que y toma el valor de 1 si y_i = 0, y cero en cualquier otro caso, entonces la función de log-verosimilitud conjunta, después de omitir las constantes, es:

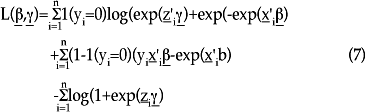
Esta función puede utilizarse para encontrar los estimadores de β (de interés primordial), así como γ. Vale la pena señalar que aunque aquí se ha hecho la derivación de la función de log-verosimilitud en términos del modelo de regresión Poisson cero-inflado, es también posible hacerlo para el modelo de regresión binomial negativa cero-inflado.

Modelos de regresión Hurdle

Al igual que el modelo de regresión para datos de conteo cero-inflado, el modelo Hurdle asume la presencia de una mezcla de distribuciones, sólo que dicho modelo tiene una interpretación en dos partes.^* La primera se refiere a un modelo con variable de respuesta binaria y la segunda a un modelo de datos de conteo truncado-en-cero. En consecuencia, esta configuración en dos partes permite la interpretación de que los valores positivos se generan toda vez que el umbral (Hurdle) en cero se ha cruzado. Por consiguiente, la primera parte modela la probabilidad de que el umbral sea cruzado, mientras que la segunda modela el valor esperado de los valores positivos.

De manera un poco más formal, el modelo Hurdle puede especificarse como sigue. Puesto que se asume una mezcla de dos distribuciones, los momentos de dichas distribuciones difieren de una distribución Poisson y pueden especificarse como sigue:

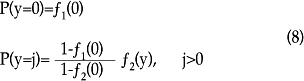
el cual se colapsa al modelo Poisson sólo si f₁(·) = f₂(·). En otras palabras, no se asume que los procesos que generaron los ceros y los valores positivos sean iguales.

En términos más simples, el modelo Hurdle es una mezcla finita generada mediante la combinación de una función de densidad que origina los ceros, y otra función de densidad que produce los valores positivos. De allí que los momentos del modelo Hurdle están determinados por la probabilidad de cruzar el umbral y por los momentos de la función de densidad truncada-en-cero, es decir:

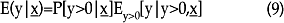
Por lo tanto, el modelo global, con ceros y valores positivos, se utiliza para estimar los parámetros vinculados con ambas densidades.

Para estimar los parámetros del modelo Hurdle se puede utilizar alguna distribución de probabilidad para variables de conteo (Poisson o binomial negativa), sólo que sin perder de vista que se tiene una variable truncada-en-cero.

Si se utiliza, por ejemplo, la distribución binomial negativa con función varianza cuadrática y se especifican las siguientes cantidades:

μ1i = exp(xi,β1)	media condicional para el caso de que el conteo sea igual a cero
μ2i = exp(xi,β2)	media condicional para el caso de que el conteo sea positivo, j = {1,2, ...}
1[yi∈J] = 1	Si yi es positiva
1[yi∈J] = 0	Si yi = 0

se pueden calcular entonces las siguientes probabilidades:

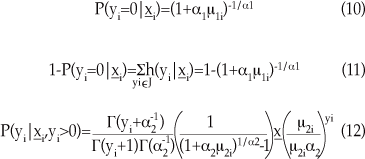
En (10) se define la probabilidad de que la variable de conteo sea igual a cero, mientras que en (11) se define la probabilidad de que el umbral sea cruzado. Por último, (12) es la distribución binomial negativa, con función de varianza cuadrática, truncada-en-cero.

Si se emplean estas probabilidades se puede especificar la función de log-verosimilitud en dos partes, a saber:

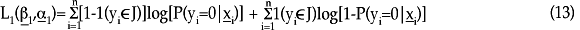
y

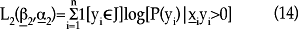
así que

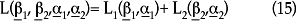
Aquí, L(β₁,α₁) es la log-verosimilitud para el proceso binario que divide a las observaciones en ceros y valores positivos; y L(β₂,α₂) es la log-verosimilitud relacionada con la parte truncada-en-cero con una distribución binomial negativa para los valores positivos. Dado que se asume que estos dos procesos son independientes,¹¹ la función global puede maximizarse al trabajar por separado con las dos respectivas funciones de log-verosimilitud.

Mullahy¹⁵ fue quien primero desarrolló esta clase de modelos Hurdle en el contexto del consumo diario de bebidas, aunque lo hizo mediante el uso de las distribuciones Poisson y geométrica, mientras que los resultados presentados aquí se han elaborado a partir de la distribución binomial negativa según Cameron y Trivedi.¹¹

 

Material y métodos

Con el objetivo de ilustrar la aplicación de los modelos descritos hasta aquí, se utilizará información concerniente al uso de servicios de salud dentro de la Encuesta de Evaluación del Seguro Popular (2005-2006). King y colaboradores han descrito los detalles sobre el diseño y características de la encuesta.¹⁶ El estudio recibió la aprobación de las comisiones de Ética y Bioseguridad del Instituto Nacional de Salud Pública.

Entre otros motivos, la Encuesta de Evaluación del Seguro Popular se diseñó para determinar si la afiliación al Seguro Popular tendría algún efecto sobre el uso de los servicios de salud, en el entendido de que la oferta de servicios del SP de manera gratuita^** podría permitir que las familias afiliadas obtuvieran un mayor acceso a los servicios de salud.

En ese sentido, la encuesta cuenta con información relativa al uso de los servicios de salud tanto para la consulta externa como para los datos de hospitalización, además de contar con dos mediciones, la basal y la de seguimiento, llevada a cabo 11 meses después. En particular, y para los análisis aquí presentados, se pretende evaluar el efecto del SP sobre la probabilidad de uso de los servicios de salud (consulta externa) y sobre la intensidad de uso de dichos servicios (número de consultas), mediante la aplicación del estimador de diferencias-en-diferencias.¹⁷ Para ello se tiene una muestra de 21 537 individuos que cuentan con información sobre estas variables.

Para los modelos de regresión utilizados se han tomado en cuenta, además del estatus de afiliación al SP, aquellas covariables consideradas en las publicaciones como relevantes para explicar el uso de los servicios de salud, tales como a) nivel individual: sexo, edad, nivel educativo, condición indígena, estado de unión, condición laboral, condición de aseguramiento, enfermedad crónica, percepción del estado de salud; b) nivel hogar: tamaño del hogar, nivel socioeconómico, afiliación a Oportunidades; y c) nivel localidad: condición de ruralidad.

Por último, para comparar los modelos analizados se utiliza el criterio de información de Akaike (AIC).^6,7 Y, con la finalidad de homogeneizar la comparación entre modelos en relación con el estimador vinculado con la afiliación al SP, los resultados se presentan en términos de efectos marginales. Todos los análisis incorporan el hecho de que se tiene un diseño pareado a nivel localidad mediante la inclusión de un efecto fijo (variable indicadora) a nivel de localidad, y se realizaron en el paquete estadístico R.¹⁸

 

Resultados

La figura 1 muestra la distribución para el número de consultas externas. Es posible observar una elevada concentración de valores en cero, un total de 10 552 observaciones (38.89%), lo cual puede introducir mayor variabilidad de la que nominalmente asume el modelo Poisson. De manera adicional, los datos contienen más ceros de los que serían predichos por un modelo Poisson con media de 1.58. Es decir, bajo la presuposición de una distribución Poisson se esperaría observar un total de 27 135*e^1.58 = 5 589 ceros, 47% menos que la frecuencia observada.

En el cuadro I se presentan los resultados para los modelos Poisson, binomial negativo (función de varianza lineal, NB1) y binomial negativo (función de varianza cuadrática, NB2). Para los tres modelos, el efecto del SP sobre el número de consultas externas es altamente significativo. Por otro lado, los resultados muestran, según el valor de AIC, que los modelos de regresión binomial negativa son una mejor opción que el modelo Poisson, lo cual se corrobora también al llevar a cabo la prueba del cociente de verosimilitudes, LR_NB1=12,145, LR_NB2=12,115, ambas significativas (p<0.001). Además, los estimadores del parámetro de dispersión (a) para NB1 y NB2 son estadísticamente distintos de cero (p<0.001), lo que significa que existe evidencia de sobredispersión. Finalmente, al comparar estos dos modelos, el valor de AIC muestra que es preferible el modelo NB1.

Los resultados de los modelos de regresión binomial negativa cero-inflado y Hurdle, con función de varianza lineal, se muestran en el cuadro II. Como se mencionó en la introducción, estos modelos tienen una especificación en términos de mezcla de distribuciones, razón por la cual los resultados de ambos modelos se encuentran divididos en dos secciones.

Para el modelo cero-inflado, la primera sección incluye los resultados al modelar la probabilidad de ocurrencia de los ceros y se han incluido aquellas variables que pueden explicar dicha ocurrencia.^*** Es posible advertir que el hecho de ser mujer implica una menor probabilidad de no utilizar los servicios de salud, al igual que tener una mala / muy mala percepción del estado de salud, entre otros datos. En cuanto a los valores positivos, que en este contexto tienen una interpretación de intensidad de uso, los datos muestran que el efecto del SP es altamente significativo para incrementar el uso de servicios de consulta externa. Por su valor de AIC, este modelo debe preferirse sobre los modelos Poisson, NB1 y NB2. En cuanto al parámetro de dispersión, su valor es significativamente distinto de cero, lo que evidencia una vez más la presencia de sobredispersión.

Por su parte, los resultados del modelo Hurdle están presentados en dos partes; en la primera se modela la probabilidad de uso, mientras que en la segunda se modela la intensidad de uso. Aquí, el efecto del SP es significativo tanto para la probabilidad de uso de los servicios de consulta externa como para incrementar el número promedio de consultas externas. También es significativo (distinto de cero) el valor del parámetro de dispersión, y el valor de AIC de este modelo es el más bajo de los cinco modelos comparados, lo cual sugiere que el modelo Hurdle es el que mejor se ajusta a los datos observados.

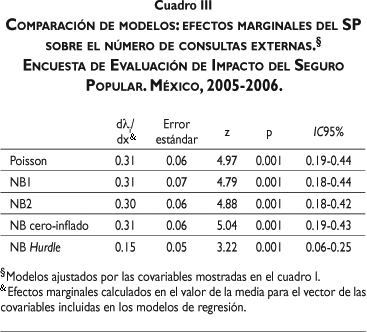
Por último, en el cuadro III figuran los resultados de la comparación entre modelos en relación con el efecto del SP en términos de efectos marginales. Los modelos Poisson, NB1, NB2 y NB cero-inflado muestran estimadores similares, en los cuales se puede observar en general que el número promedio de visitas de consulta externa para familias beneficiarias del SP es 0.3 veces más grande respecto de las familias no beneficiarias, en tanto que para el modelo Hurdle esta cantidad es de 0.15.

 

 

Discusión

Las variables expresadas como un conteo pueden hallarse prácticamente en cualquier ámbito de aplicación de la salud pública. En el contexto particular del uso de servicios de salud, su aplicación se ha extendido, ya que numerosos estudios utilizan como variable de respuesta una variable de conteo. A pesar de que el modelo Poisson es el más empleado cuando se tiene una variable de conteo, no existe una práctica generalizada en cuanto al tipo del modelo de regresión que debe utilizarse, aun cuando existen una gran variedad de modelos que pueden utilizarse.^9,11 En este artículo se han revisado algunas de las medidas más empleadas para construir un modelo de regresión cuando la variable de interés es un conteo.

Los resultados muestran que los estimadores puntuales de los cinco modelos son similares, aunque difieren en el valor de los estimadores de sus errores estándar, y por tanto en los niveles de significancia, sobre todo para el modelo Poisson. Este fenómeno se reconoce en la bibliografía^7,9,11 y es atribuible a la presencia de sobredispersión; en consecuencia, los resultados concuerdan con lo esperado desde el punto de vista teórico.

En este sentido, todos los modelos que han incorporado un parámetro adicional para modelar la dispersión tienen un valor de AIC menor al del Poisson, lo que confirma la importancia de tomar en cuenta el hecho de que la media y varianza para una variable de conteo no son casi nunca iguales.⁹ Se debe resaltar que en este artículo se ha determinado la significancia del valor del parámetro de dispersión a a partir de la estimación hecha por los modelos mismos de regresión binomial negativa, aunque en las publicaciones estadísticas existen diversas pruebas de hipótesis relacionadas con este estimador.^19-21

Los resultados muestran que el modelo Hurdle es el que exhibe un mejor ajuste para los datos de uso de servicios de consulta externa, de acuerdo con sus supuestos y el valor de AIC, y que de los otros cuatro modelos, el binomial negativo cero-inflado podría ser una opción viable, sin perder de vista que puede sobreestimar el efecto de las covariables de interés. Es decir, y de acuerdo con los resultados en relación con los valores de AIC, es posible pensar que el efecto del SP lo sobre-estiman los modelos Poisson, NB1, NB2, y NB cero-inflado, pero aun así el efecto es significativo bajo el modelo Hurdle; esto indica que el SP incrementa el número de consultas externas, además de la probabilidad de uso de estos servicios de consulta externa. Lo anterior es consistente con los hallazgos notificados en la bibliografía, en la cual se analiza si el modelo Hurdle es un mejor punto de partida que los modelos de regresión binomial negativa.^1,3,4

Por último, esta presentación se ha restringido a cinco modelos de regresión específicos para datos de conteo y han quedado fuera otras propuestas, muchas de ellas detalladas en las revisiones monográficas de Cameron-Trivedi¹¹ y Hilbe.⁹ No obstante, hay tres que en particular vale la pena mencionar. Primero, y sin dejar de reconocer la complejidad vinculada con el uso de servicios de salud, se ha hecho uso de los modelos de ecuaciones estructurales,^10,22,23 los cuales han mostrado cierta flexibilidad para modelar las relaciones de causalidad entre las variables relacionadas con el uso de servicios de salud. En segundo lugar aparecen los modelos de clase latente o mezclas finitas, los cuales se han aplicado también en el estudio del uso de servicios de salud.^24,25 De manera específica, estos modelos son útiles porque permiten modelar de forma directa la heterogeneidad no observada; de ahí la presencia de sobredispersión o subdispersión. Por último, en fecha reciente se ha propuesto el uso combinado de los modelos de clase latente con el modelo Hurdle?⁶ En esta clase de modelos se pretende modelar la heterogeneidad no observada mediante la introducción de clases latentes, pero se conserva el hecho de que el uso de servicios de salud puede ser el resultado de un proceso en dos partes: la decisión de utilizar y la frecuencia del uso.

Agradecimientos

Los autores agradecen a la Secretaría de Salud, en particular a la Dirección General de Evaluación del Desempeño, por la autorización para el uso de la base de datos de la Encuesta de Evaluación del Seguro Popular, 2005-2006. Los resultados presentados constituyen un análisis y edición adicional de los autores. Los puntos de vista expresados no representan una posición oficial de la Secretaría de Salud, y son sólo responsabilidad de los autores.

 

Referencias

1. Pohlmeier W, Ulrich V. An econometric model of the two-part decision process in the demand for health. J Hum Res 1995;30(2):339-361.         [ Links ]

2. Santos-Silva JMC,Windmeijer F. Two-part multiple spell models for health care demand. J Econo 2001;104(1):67-89.         [ Links ]

3. Gerdtham UG. Equity in health care utilization: further tests based on Hurdle models and swedish micro data. Health Econo 1997;6:303-319.         [ Links ]

4. Grootendorst PV. A comparison of alternative models of prescription drug utilization. Health Econo 1995;4:183-198.         [ Links ]

5. Deb P, Trivedi PK. Demand for medical care by the elderly: a finite mixture approach. J Appl Econo 1997;12:313-336.         [ Links ]

6. Hardin J, Hilbe J. Generalized linear models and extensions. 2nd ed. Texas: Stata Press, 2007.         [ Links ]

7. McCullagh P, Nelder JA. Generalized linear models. 2nd ed. New York: Chapman & Hall, 1989.         [ Links ]

8. Dobson A, Barnett A. An introduction to generalized linear models. 3rd ed. New York: Chapman & Hall/CRC, 2008.         [ Links ]

9. Hilbe J. Negative binomial regression. Cambridge: Cambridge University Press, 2007.         [ Links ]

10. Congdon P, Almog M, Curtis S, Ellerman R. A spatial structural equation modelling framework for health count responses. Stat Med 2007;26:5267-5284.         [ Links ]

11. Cameron AC, Trivedi PK. Regression analysis of count data. Cambridge: Cambridge University Press, 1998.         [ Links ]

12. Efron B, Tibshirani R. An introduction to the bootstrap. New York: Chapman & Hall/CRC, 1993.         [ Links ]

13. Jones AM. Applied health economics. Oxford: Routledge, 2007.         [ Links ]

14. Lambert D. Zero-inflated poisson regression with an application to defects in manufacturing. Technometrics 1992;34:1-14.         [ Links ]

15. Mullahy J. Specification and testing of some modified count data models. J Econo 1986;33:341-365.         [ Links ]

16. King G. A "politically robust" experimental design for public policy evaluation, with application to the Mexican Universal Health Insurance Program. J Pol Anal Manag 2007;26(3):479-506.         [ Links ]

17. Ashenfelter O, Card D. Using the longitudinal structure of earnings to estimate the effect of training programs. Rev Econo Stat 1985;67(4):648-660.         [ Links ]

18. R Development Core Team. [sitio de internet]. R: a language and environment for statistical computing. R Foundation for Statistical Computing,Vienna,Austria 2008. ISBN 3-900051-07-0. [Consultado 2009 feb 10]. Disponible en http://www.R-project.org.         [ Links ]

19. Cameron AC, Trivedi PK. Econometric models based on count data: comparisons and applications of some estimators and tests. J Appl Econo 1986;(1):29-53.         [ Links ]

20. Cameron AC, Trivedi PK. Regression-based tests for overdispersion in the poisson model. J Econo 1990;46:347-364.         [ Links ]

21. Dean C, Lawless JF. Tests for detecting overdispersion in poisson regression models. J Am Stat Ass 1989;84:467-472.         [ Links ]

22. Ellencweig AY, Pagliccia N. Utilization patterns of cohorts of elderly clients: a structural equation model. Health Serv Res 1994;29:225-245.         [ Links ]

23. Andersen AS, Laake P A causal model for physician utilization: analysis of Norwegian data. Med Care 1983;21:266-278.         [ Links ]

24. Deb P, Trivedi PK. The structure of demand for health care: latent class versus two-part models. J Health Econo 2002;21:601-625.         [ Links ]

25. Jimenez-Martin S. Latent class versus two-part models in the demand for physician services across the European Union. Health Econo 2002;11:301-321.         [ Links ]

26. Bago d'Uva T. Latent class models for health care utilization. Health Econo 2006;15:329-343.         [ Links ]

 

 

Solicitud de sobretiros:
Betty Manrique-Espinoza
Centro de Investigación en Evaluación y Encuestas, INSP
Av. Universidad 655, col. Santa María Ahuacatitlán
62100 Cuernavaca, Morelos, México
Correo electrónico: bmanrique@insp.mx, bs_manrique@yahoo.com.mx

Fecha de recibido: 16 de febrero de 2009
Fecha de aprobado: 17 de junio de 2009

 

 

* Por esa razón esta clase de modelos se conoce comúnmente como two-part hurdle models.
** Es importante mencionar que el costo del SP es nulo para las familias que se ubiquen en los dos primeros deciles de ingreso, mientras que para las demás familias se realiza una aportación proporcional al ingreso.
*** Aunque se ha incluido todo el vector de covariables utilizadas para modelar el valor esperado del conteo E(Y), no existe restricción alguna para incluir un subconjunto del total de covariables, aunque es importante notar que la elección de estas covariables debe realizarse, como siempre sucede, con un marco teórico que justifique su elección.