Research
High Energy Physics
Initial State Radiation and Beamstrahlung in the production of a resonance of mass mZ' in 3-3-1 model
C. A. Morgan Cruza
G. H. Ramírez Ulloaa
A. I. Rivasplata Mendozaa
K. J. Ramos Villalobosa
J. F. Rabanal Muñoza
R. J. Gil Ramíreza
J. E. Cieza Montalvob
a Universidad Nacional de Trujillo, Departamento de Física, Av. Juan Pablo II S/N; Ciudad Universitaria, Trujillo, La Libertad, Perú.
b Instituto de Física, Universidade do Estado do Rio de Janeiro, Rua São Francisco Xavier 524, 20559-900 Rio de Janeiro, RJ, Brazil.
Abstract
In this work we study the effects of Initial State Radiation (ISR) and Beamstrahlung (BS), in the production of Z’ in the 3-3-1 model with heavy leptons. The impact of the ISR and BS on precision measurements strongly afects the behaviour of the production cross section around the resonance points: mZ'=5976.43(6830.21; 8539.47) GeV for vχ=3.5(4.0; 5.0) TeV, at the Compact Linear Collider (CLIC).
Keywords: Charged Higgs; 3-3-1 model; initial state radiatio; beamstrahlung
1. Introduction
The SM provides a very good description of all the phenomena related to hadron and lepton colliders. This includes the Higgs boson which appears as elementary scalar and which arises through the breaking of electroweak symmetry. So, on 4 July 2012, the discovery of a new particle with a mass measured by CMS Collaboration to be 125.35 GeV was announced; physicists suspected that it was the Higgs boson. Since then, the particle has been shown to behave, interact, and decay in many of the ways predicted for Higgs particles by the Standard Model, as well as having even parity and zero spin, two fundamental attributes of a Higgs boson. This also means it is the first elementary scalar particle discovered in nature, [1]. Any discovery of a charged Higgs boson would be confirmation of new physics and the CLIC can admit or exclude such a probability.
Different types of Higgs bosons, if they exist, may lead us into new realms of physics beyond the SM. Since the SM leaves many questions open, there are various extensions. For instance, if the SM at high energies is restrained in the Grand Unified Theory (GUT), subsequently the Higgs bosons related with GUT symmetry breaking required masses of order MX∼O(1015) GeV. Supersymmetry [2] supplies a solution to hierarchy problem through the cancellation of the quadratic divergences via fermionic and bosonic loops contributions [3,4,5,6]. Furthermore, the Minimal Supersymmetric extension of the SM can be obtained as an effective theory of supersymmetric GUT [7,8,9].
There are also other class of models based on SU(3)C⊗SU(3)L⊗U(1)N gauge symmetry (3-3-1 model) [10,11,12], where the anomaly cancellation mechanisms occur when the three basic fermion families are considered and not family by family as in the SM. This mechanism is peculiar because it requires that the number of families is an integer multiple of the number of colors. This feature combined together with the asymptotic freedom, which is a property of quantum chromodynamics, requires that the number of families is three. Moreover, according to these models, the Weinberg angle is restricted to the value sW2=sin2θW<1/4 in the version of heavy-leptons [10]. Thus, when it evolves to higher values, it shows that the model loses its perturbative character when it reaches to mass scale of about 4 TeV [13]. Hence, the 3-3-1 model is one of the most interesting extensions of the SM and is phenomenologically well motivated to be probed at the CLIC and other accelerators.
Future TeV-scale linear colliders will cause a significant degradation of the energy of the center of mass during the collision of electrons and positrons, so corrective effects such as Beamstrahlung (BS) [14,15,16,17], that is, the Radiation from a beam of charged particles in a linear collider, due to its interaction with the electromagnetic field of the other beam, causes a bending in the path of the particles under the influence of such electromagnetic fields. During this bending, the particles radiate photons, causing a loss of beam energy.
Another correction that must be made in the production of new particles is due to initial and final state radiation (ISR) [18], which is perturbative, it occurs in any process that contains electrically charged or colored particles, either in the initial state, where one of the incoming particles emits radiation before the interaction with the others, so reducing the beam energy previously to the momentum transfer, as in the final state and manifests with gluon or photon radiation.
So, these corrective effects such as BS and ISR will make it possible to have more precise measurements of the cross section, near the point of resonance.
This paper is organized as follows. In Sec. 2 we discuss the relevant features of the model. In Sec. 3 we compute the total cross sections and introduce the ISR and BS effects. Finally in Sec. 4 we present our concluding remarks.
2 Relevant features of the model
If there exist any model beyond the standard model (BSM), then it is no strange that it is still hidden in the scalar sector. As one of the simplest BSM models, is the 3—3—1 model, which has been extensively investigated in the literature.
These is a promissory model which is based on the SU(3)C⊗SU(3)L⊗U(1)N (3-3-1 for short) semi simple symmetry group [10], which contains both charged Higgs bosons. In this model the three Higgs scalar triplets
η=η0η1-η2+∼3,0,ρ=ρ+ρ0ρ++∼3,1,χ=χ-χ--χ0∼3,-1,
(1)
generate the fermion and gauge boson masses in the model. The neutral scalar fields develop the vacuum expectation values (VEVs) 〈η0〉=vη, 〈ρ0〉=vρ and 〈χ0〉=vχ, with vη2+vρ2=vW2=(246 GeV )2. The pattern of symmetry breaking is
SU(3)L⊗U(1)N⟼〈χ〉SU(2)L⊗U(1)Y⟼〈η,ρ〉U(1)em
and so, we can expect vχ≫vη,vρ. The η and ρ scalar triplets give masses to the ordinary fermions and gauge bosons, while the χ scalar triplet gives masses to the new fermions and new gauge bosons. The most general, gauge invariant and renormalizable Higgs potential is
η,ρ,χ=μ12η†η+μ22ρ†ρ+μ32χ†χ+λ1η†η2+λ2ρ†ρ2+λ3χ†χ2+η†η[λ4ρ†ρ+λ5χ†χ]+λ6ρ†ρχ†χ+λ7ρ†ηη†ρ+λ8χ†ηη†χ+λ9ρ†χχ†ρ+λ10η†ρη†χ+12fϵijkηiρjχk+ H. c. .
(2)
Here f is a constant with dimensions of mass and the λi, (i = 1,…,10) are dimensionless constants with λ3 < 0 from the positivity of the scalar masses. The term proportional to λ10 violates lepto-barionic number so that, it was not considered in the analysis of the Ref. [19] (another analysis of the 3-3-1 scalar sector are given in Ref. [20] and references cited therein). We can notice that this term contributes to the mass matrices of the charged scalar fields, but not to the neutral ones. However, it can be checked that in the approximation vχ≫vη,vρ we can still work with the masses and eigenstates given in Ref. [19]. Here this term is important to the decay of the lightest exotic fermion. Therefore, we are keeping it in the Higgs potential.
We present the Yukawa Lagrangians that respects the gauge symmetry and that is given in several papers (see, for example, [21]).
-Ll=12{1vρ[cων¯UνlH1++vρ+sωH10-cωH20e-¯+sϕP+¯UPlH++]MlGRe-+1vχ[cων¯VνPH2-+cϕe-¯VlPH--+vχ+H30+ih0P+¯]MPGRP+}+H.c,
(3)
Where GR = 1 + γ5, the Cabbibo-Kobayashi-Maskawa mixing matrix, Uνl,UPl,VνP,VlP are arbitrary mixing matrices, Ml=diagme mμ mτ, MP=diagmE mM mT.
Symmetry breaking is initiated when the scalar neutral fields are shifted as φ=vφ+ξφ+iζφ, with φ=η0,ρ0,χ0. Thus, the physical neutral scalar eigenstates H10,H20,H30 and h0 are related to the shifted fields as
ξηξρ≈1vWvηvρvρ-vηH10H20,ξχ≈H30,ζχ≈h0,
(4)
and in the charge scalar sector we have
η1+≈vρvWH1+,ρ+≈vηvWH2+,χ++≈vρvχH++,
(5)
with the condition that vχ≫vη,vρ[19].
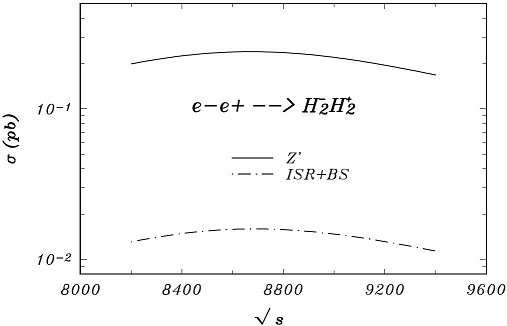
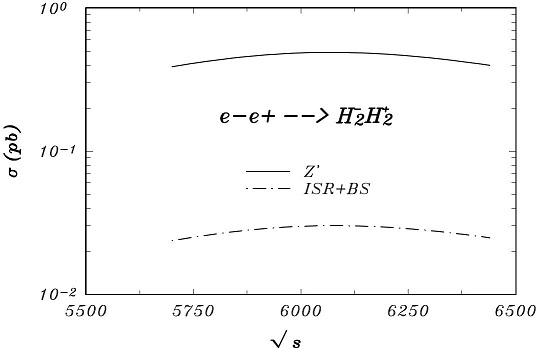
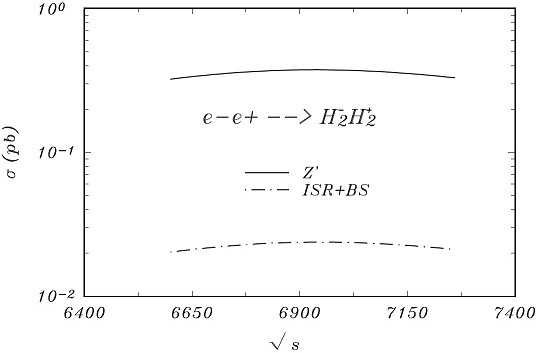
In this work we introduce the ISR and BS as corrections effects to the cross section around the resonances points: mZ'=5976.43 GeV, mZ'=6830.21 GeV and mZ'=8539.47 GeV for vχ=3.5(4.0;5.0) TeV, at the CLIC with 3 and 5 TeV [22].
3 Cross section production
The process e-e+→H2-H2+, take place through the exchange of the bosons γ, Z and Z’ in the s channel. Then using the Yukawa Lagrangians written above we evaluate the differential cross section for the H2±
dσ^dΩ=164π2s^(Mγ2¯+MZ2¯+MZ'2¯+2ReMγMZ¯+2ReMγMZ'¯+2ReMZMZ'¯).
(6)
Writing separately the cross-sections, we will have
dσ^γdcosθ=βH2±α2π(ΛγH2-H2+)216s3sin2θWŁstu,
(7)
dσ^Zdcosθ=βH2±α2π(ΛZH2-H2+)2(gV2+gA2)64sin4θWcos2θWs(s-mZ2+imZΓZ)2Łstu,
(8)
dσ^Z'dcosθ=βH2±α2π(ΛZ'H2-H2+)2(gV'2+gA'2)192sin4θWcos2θWs(s-mZ'2+imZ'ΓZ')2Łstu,
(9)
dσ^γ-Zdcosθ=-βH2±α2π(ΛγH2-H2+)(ΛZH2-H2+)(gV)16sin3θWcosθWs2(s-mZ2+imZΓZ)Łstu,
(10)
dσ^γ-Z'dcosθ=-βH2±α2π(ΛγH2-H2+)(ΛZ'H2-H2+)gV'163sin3θWcosθWs2(s-mZ'2+imZ'ΓZ')Łstu,
(11)
dσ^Z-Z'dcosθ=-βH2±α2π(ΛZH2-H2+)(ΛZ'H2-H2+)(gVgV'+gAgA')323sin4θWcos2θWs(s-mZ2+imZΓZ)(s-mZ'2+imZ'ΓZ')Łstu,
(12)
where we have defined the Łstu parameter
Łstu=s(s-4mH2±2)-(t-u)2,
and the βH2± is the Higgs velocity in the c.m. of the process which is equal to
βH2±=1-4mH2±2s,
and t and u are
t=mH2±2-s21-βH2±cosθ,
u=mH2±2-s21+βH2±cosθ,
where θ is the angle between the Higgs and the incident electron in the CM frame.
The primes (′) are for the case when we take a Z’ boson, ΓZ'[25,23], are the total width of the
Z’ boson, gV,A are the standard lepton
coupling constants, gV’,A’ are the 3-3-1 lepton coupling
constants, s is the center of mass energy of the
e—e+ system, g=4 π α/sinθW and α is the fine structure constant, which we take equal to α= 1/128..
For the Z’ boson we take mZ'=5.9-8.6 TeV [26,27], since mZ' is proportional to the VEV vχ
[19,11,12]. For the standard model parameters,
we assume Particle Data Group values, i.e.,
mz = 91.19 GeV, sin2θW=0.2315, and MW=80.33 GeV [28], the velocity of the Higgs in the c.m of the
process we denote through βH2±, t and u are the kinematic invariants.
We have also defined the ΛγH2-H2+ as the coupling constants of the γ to Higgs H2±, the ΛZH2-H2+ as the coupling constants of the Z to Higgs H2± and the ΛZ'H2-H2+ as being the coupling constants of the Z’ to Higgs H2±.
ΛγH2-H2+=tW(vχ2-vρ2)1+4tW2 (vχ2+vρ2),
ΛZH2-H2+=-vρ2(1+6tW2)-2t2vχ2(vχ2+vρ2)(1+4tW2)(1+3tW2),
ΛZ'H2-H2+=vρ2(6tW2-1)+2vχ2(vχ2+vρ2)(1+3tW2),
Where
tW=sW1-4sW2,
And
sW=sinθW.
We will now consider the effects of ISR and BS. The ISR corrections to the cross section for
e+e— annihilations at
high energies are presented. These corrections are not at tree-level but with
accuracy up to the α2 terms. The cross section will be folded with the
distributions given by [14,18]. Then we have
σ(s)=∫dχσZ'((1-χ)s)H(χ,s)
(13)
where σZ' represents the resonance cross section, χ=1-4me/s and H(χ,s) is a radiator function that summarize the results of the ISR corrections.
H(χ,s)=Δ'2βχβ-1(1-π2β2/24)+Δ'2βχβ2-1/2[(1-χ)-β2-1]-Δ'β/2[(2-χ)χβ2-β/2[(2-χ)ln(1-χ)-χ]]+β2/16[(2-χ)[2ln(1-χ)-4lnχ]-4[ln(1-χ)]/χ-6+3χ],
(14)
where we have for
β=2απlog(sme2-1),
(15)
Δ'=1+3β8.
(16)
On the other side, BS is an effect that occurs in high-energy
e+e— collisions, when
each beam of e+(e—), due to
its high density, generates a strong electromagnetic field. So when the other beam
passes through this electromagnetic field, its path is curved and the curved
particles will radiate photons. This energy loss is called BS.
The effective differential cross section for a final state with the effect of the BS is related to the effective differential cross section without effect, by means of the following formula:
dσ(s,y)dy=WBS(y) σZ'(s(1-y)),
(17)
where
WBS(y)=0.2ασzγλΥ21-yΥy×exp-23Υ1-yy+41-y,
(18)
is the function that describes the probability density of the BS and the variable y is the fraction of energy lost through emitted photons from the BS, ϒ is the effective beamstrahlung parameter, which is given by
Υ=56re2γNασz(σx+σy),
(19)
where re is the radius of the electron, N the number of particles
per beam, γ the Lorentz factor, α the fine structure constant and (σx,
σy, σz) are the beam parameters.
Therefore, the effective cross section, considering the BS effect is:
σ=∫σZ'(s(1-y)) WBS(y)dy.
(20)
4 Results and conclusions
Precision tests of the 3-3-1 theory around the Z’ are in this context a
relevant question. In particular a significant role is played by the ISR and BS
corrections to the initial electron-positron state. The physics involved in the
problem of ISR and BS corrections is related to the emission of photons in the
process of annihilation of electrons and positrons and its effect on the resonance
peak. That is, in the production of a resonance of mass mz' with colliding beams of total energy of the center of mass s=2E, the emission of hard and soft photons occurs.
The impact of the initial state radiaton (ISR) and beamstrahlung (BS) on precision measurements strongly affects the behaviour of the production cross section around the resonance peaks, modifying as the shape as the size, so Figs. 1, 2 and 3 shows the cross section with and without ISR + BS around the resonances points: mZ'=5976.43 GeV, mZ'=6830.21 GeV and mZ'=8539.47 GeV for vχ=3.5(4.0;5.0) TeV, at the CLIC with 3 and 5 TeV. As can be seen the peak of the resonance shifts to the right and is lowered as a result of the ISR + BS effects.
References
1. The CMS Collaboration, Constraints on anomalous Higgs boson
couplings using production and decay information in the four-lepton final state,
Phys. Lett. B
775 (2017) 1,
https://doi.org/10.1016/j.physletb.2017.10.021.
[ Links ]
2. J. Wess and B. Zumino, Supergauge transformations in four
dimensions, Nucl. Phys. B
70 (1974) 39,
https://doi.org/10.1016/0550-3213(74)90355-1.
[ Links ]
3. J. Wess and B. Zumino, A lagrangian model invariant under
supergauge transformations, Phys. Lett. B
49 (1974) 52,
https://doi.org/10.1016/0370-2693(74)90578-4.
[ Links ]
4. J. Iliopoulos and B. Zumino, Broken supergauge symmetry and
renormalization, Nucl. Phys. B
76 (1974) 310,
https://doi.org/10.1016/0550-3213(74)90388-5.
[ Links ]
5. S. Ferrara, J. Iliopoulos and B. Zumino, Supergauge invariant
Yang-Mills theories, Nucl. Phys. B 77 (1974) 413,
https://doi.org/10.1016/0550-3213(74)90559-8.
[ Links ]
6. E. Witten, Dynamical breaking of supersymmetry, Nucl.
Phys. B 188 (1981) 513,
https://doi.org/10.1016/0550-3213(81)90006-7.
[ Links ]
7. S. Dimopoulos and H. Georgi, Softly broken supersymmetry and
SU(5), Nucl.Phys. B
193 (1985) 150,
https://doi.org/10.1016/0550-3213(81)90522-8.
[ Links ]
8. S. Dimopoulos, S. Raby, and F. Wilczek, Supersymmetry and the
scale of unification, Phys. Rev. D
24 (1981) 1681,
https://doi.org/10.1103/PhysRevD.24.1681.
[ Links ]
9. L. Ibañez and G. G. Ross, Low-energy predictions in
supersymmetric grand unified theories, Phys. Lett. B
105 (1981) 439,
https://doi.org/10.1016/0370-2693(81)91200-4.
[ Links ]
10. V. Pleitez and M. D. Tonasse, Heavy charged leptons in an
SU(3)L⊗U(1)N model, Phys. Rev. D
48 (1993) 2353,
https://doi.org/10.1103/PhysRevD.48.2353.
[ Links ]
11. F. Pisano and V. Pleitez, SU3⊗U1 model for electroweak
interactions, Phys. Rev. D
46 (1992) 410,
https://doi.org/10.1103/PhysRevD.46.410.
[ Links ]
12. P. H. Frampton, Chiral dilepton model and the flavor question,
Phys. Rev. Lett.
69 (1992) 2889,
https://doi.org/10.1103/PhysRevLett.69.2889.
[ Links ]
13. A. G. Dias, Evading the few TeV perturbative limit in 3-3-1
models, Phys. Rev. D
71 (2005) 015009,
https://doi.org/10.1103/PhysRevD.71.015009.
[ Links ]
14. O. Nicrosini and Luca Trentadue, Soft photons and second order
radiative corrections to
e+e—→Z0,
Phys. Lett. B
196 (1987) 551,
https://doi.org/10.1016/0370-2693(87)90819-7.
[ Links ]
15. P. Chen, Differential luminosity under multiphoton
beamstrahlung, Phys. Rev. D
46 (1992) 1186,
https://doi.org/10.1103/PhysRevD.46.1186.
[ Links ]
16. K. Yokoya and P. Chen, Beam-beam phenomena in linear colliders, In Frontiers of Particle Beams: Intensity Limitations. (Springer, Berlin, Heidelberg, 1992), pp. 415-445. https://doi.org/10.1007/3-540-55250-237.
[ Links ]
17. O. Cakir, Production of doubly charged Higgs bosons at linear
e—
e— colliders, New J. Phys.
8 (2006) 145,
https://doi.org/10.1088/1367-2630/8/8/145.
[ Links ]
18. E. A. Kuraev and V. S. Fadin, Yad. Fiz, On Radiative Corrections
to e+
e— Single Photon Annihilation at High-Energy,
Sov. J. Nucl. Phys. 41 (1985)
466.
[ Links ]
19. M. D. Tonasse, The scalar sector of 3-3-1 models, Phys.
Lett. B
381 (1996) 191,
https://doi.org/10.1016/0370-2693(96)00481-9.
[ Links ]
20. N. T. Anh, N. A. Ky and H. N. Long, The Higgs sector in the
minimal 3-3-1 model with the most general lepton-number conserving potential,
Int. J. Mod. Phys. A
16 (2001) 541,
https://doi.org/10.1142/S0217751X01003184.
[ Links ]
21. J. E. Cieza Montalvo, N.V. Cortez, J. S Borges and M.D. Tonasse,
Searching for doubly charged Higgs bosons at the LHC in a 3-3-1 Model,
Nucl. Phys. B
756 (2006) 1,
https://doi.org/10.1016/j.nuclphysb.2006.08.013.
[ Links ]
22. CLIC Physics Working Group Collaboration, Physics at the CLIC
Multi-TeV Linear Collider, Geneva: CERN
005 (2004) 226,
https://doi.org/10.5170/CERN-2004-005.
[ Links ]
23. J. E. Cieza Montalvo and M. D. Tonasse, Pairs of charged
heavy-leptons from an SU(3)L⊗U(1)N model at
CERN LHC, Nucl. Phys. B
623 (2002) 325,
https://doi.org/10.1016/S0550-3213(01)00643-5.
[ Links ]
24. J. E. Cieza Montalvo and M. D. Tonasse, Pairs of charged heavy
fermions from an SU(3)L⊗U(1)N model at
e+
e— colliders, Phys. Rev. D
67 (2003) 075022,
https://doi.org/10.1103/PhysRevD.67.075022.
[ Links ]
25. J. E. Cieza Montalvo and M. D. Tonasse, Neutral Higgs bosons in
the SU(3)L⊗U(1)N model, Phys. Rev. D
71 (2005) 095015,
https://doi.org/10.1103/PhysRevD.71.095015.
[ Links ]
26. P. S. Bhupal Dev, R. N. Mohapatra, Unified Explanation of the
eejj, Diboson, and Dijet Resonances at the LHC,
Phys. Rev. Lett.
115 (2015) 181803,
https://doi.org/10.1103/PhysRevLett.115.181803.
[ Links ]
27. N. Okada, S. Okada, D. Raut, Natural Z’-portal
Majorana dark matter in alternative U(1) extended standard model, Phys.
Rev. D
100 (2019) 035022,
https://doi.org/10.1103/PhysRevD.100.035022.
[ Links ]
28. J. Beringer et al. (Particle Data Group), Review of Particle
Physics, Phys. Rev. D
86 (2012) 010001,
https://doi.org/10.1103/PhysRevD.86.010001.
[ Links ]











 nueva página del texto (beta)
nueva página del texto (beta)