Optical solitons to a perturbed Gerdjikov-Ivanov equation using two different techniques

Shehata, M. S. M.; Rezazadeh, H.; Jawad, A. J. M.; Zahran, E. H. M.; Bekir, A.; Shehata, M. S. M.; Rezazadeh, H.; Jawad, A. J. M.; Zahran, E. H. M.; Bekir, A.

doi:10.31349/revmexfis.67.050704

Servicios Personalizados

Revista

Articulo

Indicadores

Links relacionados

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.67 no.5 México sep./oct. 2021 Epub 28-Mar-2022

https://doi.org/10.31349/revmexfis.67.050704

Research

Gravitation, Mathematical Physics and Field Theory

Optical solitons to a perturbed Gerdjikov-Ivanov equation using two different techniques

M. S. M. Shehata^a

H. Rezazadeh^b

A. J. M. Jawad^c

E. H. M. Zahran^d

A. Bekir^e

^{^a}Departments of Mathematics, Zagazig University, Faculty of Science, Zagazig, Egypt. e-mail: dr.maha 32@hotmail.com

^{^b}Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran. e-mail: Rezazadehadi1363@gmail.com

^{^c}Departments of Mathematics, Faculty of Science, Al Rafidain University, Iraq. e-mail: anwar jawad2001@yahoo.com

^{^d}Departments of Mathematical and Physical Engineering, Benha University, Faculty of Engineering, Shubra, Egypt. e-mail: e_h_zahran@hotmail.com

^{^e}Neighbourhood of Akcaglan, Imarli Street, Number: 28/4, 26030, Eskisehir, Turkey. e-mail: bekirahmet@gmail.com

Abstract

In this article, the perturbed Gerdjikov-Ivanov equation, describing the dynamics of propagation of solitons, is studied. The balanced modified extended tanh-function and the non-balanced Riccati-Bernoulli Sub-ODE methods are used for the first time to obtain the new optical solitons of this equation. The obtained results give an accurate interpretation of the propagation of solitons. We performed a comparison between our results and those in the literature. The efficiency of these methods for constructing the exact solutions has been demonstrated. It is shown that these different techniques reduce the large number of calculations.

Keywords: The Perturbed Gerdjikov-Ivanov (GI)-equation; the METF method; the RBSub-ODE method; Optical solitons

1. Introduction

The Gerdjikov-Ivanov (GI) equation carries the quartic nonlinearity of latter equation while ’s equation is classically explored with cubic nonlinearity, the dimensionless GI-equation is

$iqt+aqxx+bq4q+icq2q+x=0,$ (1)

where $q*x,t$ denotes the complex conjugation of the complex valued wave structure $qx,t$ with $x$ and $t$ as spatial and temporal variables. The initial and last terms of the dimensionless GI-equation stand for the linear temporal evolution of solitons and the nonlinear dispersion, respectively. All the involved parameters: $a$ , $b$ , and $c$ are real-valued constants such that $a$ gives dispersion of group velocity and $b$ is the coefficient of the quartic nonlinear term.

The famous full nonlinearity structure of the perturbed GI- equation is,

$iqt+aqxx+bq4+icq2qx +=iαqt+λqq2mx+μq2mxq,$ (2)

where $a,$ $μ$ and $λ$ represent the inter-modal dispersion, the higher-order dispersion effect and the self-steepening for short pulses, respectively, while $m$ accounts for full nonlinearity effects.

Big varieties of biological, chemical, and physical phenomena are governed by nonlinear partial differential equations (NLPDEs) which play a crucial role in nonlinear science. The analysis of such equations provides insightful physical information, useful for further applications. Many trails have been penned for the physical problems in the last years to get the analytical solutions of the NLPDEs with the recent computer technology [¹^-¹²]. A variety of powerful methods have been developed such as the $exp-ϕζ$ -expansion expansion method [¹³^,¹⁴], the ( $G'/G$ )-expansion method [¹⁵^,¹⁶], the new extended direct algebraic method [¹⁷^,¹⁸], the first integral method [¹⁹^,²⁰], the extended Jacobi elliptic function expansion method [²¹^,²²], and so on [²³^-³⁰]. Furthermore, the current analysis concentrates over one such nonlinear evolution equation, known as the GI equation [³¹]. A spectral problem and the associated perturbed GI hierarchy [³²] of nonlinear evolution equations is presented and shown that the GI hierarchy is integrable in a Liouville sense and possesses bi-Hamiltonian structure. Numerous efficient and influential methods have been projected for obtaining solutions of GI equation, such as algebra-geometric solutions [³³], soliton hierarchy [³⁴], bifurcations and travelling wave [³⁵], bright and dark soliton solutions [³⁶], Darboux transformations [³⁷] and many more being studied for more than a decade [³⁸^-⁴⁸], and Kaur and Wazwaz [⁴⁹] obtain the optical solitons for perturbed GI equation. In this paper we are going to apply the balanced modified extended tanh-function (METF) method as a new technique to get new exact solution for the perturbed GI equation.

2. The METF method

The main idea of the METF functions method is finding the exact solution of any model which can be expressed by a polynomial of $ϕζ$ controlled by the Riccati differential equation φ ⁰ = b + φ ²(ζ), ζ = x − vt where b, c are arbitrary constants to be determined later. The degree of the polynomial can be calculated by the homogenous balance between the highest order derivative term and the nonlinear term. Equating the coefficients of the different powers of $ϕζ$ to zero, we get the system of algebraic equations. This system of algebraic equations can be solved by Maple or Mathematica to determine the constants of the polynomial.

According to the proposed method the solution is,

$Hζ=a0+∑i=1Maiϕi+biϕi,$ (3)

where $ai$ , $bi$ , are constants to be determined, such that $aM≠0$ or $bM≠0$ and $ϕ$ satisfies the Riccati equation

$ϕ'=b+ϕ2$ (4)

Equation (4) admits several types of solutions according to the value of the constant $b$ , namely,

Case 1. If $b<0,$ then

$φ=--btanh⁡-bζ, orφ=--bcoth⁡-bζ.$ (5)

Case 2. If $b>0,$ then

$φ=btan⁡bζ, orφ=-bcot⁡bζ.$ (6)

Case 3. If $b=0,$ then

$φ=-1ζ$ (7)

Now, for the proposed problem in Eq. (2), let us introduce this wave transformation:

$q=uζexp⁡iψx,t,$ (8)

$qt=exp⁡iψx,t-vu'+i{w-vφ'}u,$ (9)

$qx=exp⁡iψx,tu'-i{k-φ'}u,$ (10)

$qxx=exp⁡iψx,t[u″-iku'-uφ″-u'φ'-ik-φ'u'-k-φ'2u],$ (11)

with ζ=x−vt, ψ(x,t) = − kx + wt + φ(ζ), u(ζ) represents the shape features of the wave pulse, $ψx,t$ is the phase element of the soliton, $k$ , $φ,$ $w$ , $v$ represent the soliton frequency, wave number, phase constant and velocity, respectively. Inserting (8-11) into (2), followed by uncoupling of real and imaginary parts of the equation gives a pair of equations, i.e., the real part is

$au″-w-vφ'+ak2-2αkφ'-aφ'2u+cu3k-φ'+bu5=0,$ (12)

and the imaginary part is

$αuφ″-2αk-2aφ'-cu2u'=0.$ (13)

In order to solve this pair of equations, we use the transformation

$φ'=a1u2+b1,$ (14)

where $a1$ and $b1$ denote the constant and nonlinear chirp parameters, respectively. Substitution of Eq. (14) into Eq. (13) leads to

$4a1a+cu2+2αb1-2αk-v=0.$ (15)

This gives, consequently, $a1=-c/4a$ , $b1=v/2a+k,$

$φ'=v2a+k-c4au2,$ (16)

and upon substitution of Eq. (16) in Eq. (12), we obtain

$u''-n1u+n2u3+n3u5=0,$ (17)

where

$n1=v2-4kvα-4aw4a2, n2=cv2a2, n3=b3c2+16αb16a2.$

When we set $u=H1/2$ in Eq. (17), we obtain the equation

$2HH''-H'2+4n1H2+4n2H3+4n3H4=0,$ (18)

which, after balancing the nonlinear and higher order derivative terms where we obtain that $2M+2=4M$ (hence, $M=1$ ), the solution becomes

$Hζ=A0+A1ϕζ+B1ϕζ.$ (19)

Inserting the expression of Eq. (19) in every term of Eq. (18) and equating the coefficients of each power of $ϕζ$ to zero yields a set of algebraic equations,

$3+4n3A12=0,A0+A12n2+4n3A0=0,6B1+A12b+4n1+12n2A0+8A1n33A02+22A1B1=0,A0b+2n1+12n3A1B1+4n3A0+3n2A1B1=0,3b2-4n3B12=0,A0b2+B12n2+n3A0+n3A1=0,6A1b2+B16b+4n1+4n2A0+24n3A02+16A1B1=0.$ (20)

By solving the system of (20) by any computer program, we have:

$n1=4A02,n2=-16A03,n3=2, A1=-i232, B1=0, b=0,n1=4A02, n2=-16A03, n3=2, A1=i232, B1=0, b=0,n1=-272, n2=4i6, n3=2, A0=-3i232, A1=-i232, B1=0, b=0,n1=-272, n2=-4i6, n3=2, A0=3i232, A1=-i232, B1=0,b=0,n1=-272, n2=-4i6, n3=2, A0=3i232, A1=i232, B1=0, b=0,n1=-114326-10813i, n2=4i6, n3=2, A0=-3i232, A1=-i232,B1=-3613+54i136,b=14413-216i13,n1=-114326+10813i, n2=4i6, n3=2, A0=-3i232, A1=-i232,B1=3613+54i136,b=14413+216i13,n1=-114326+10813i, n2=-4i6, n3=2, A0=3i232, A1=i232,B1=-3613-54i136,b=14413+216i13,n1=-114326+10813i, n2=-4i6, n3=2, A0=3i232, A1=i232,B1=3613-54i136,b=14413-216i13,,$

where the outlined method and the results of (1-6) imply the existence of the solution

$Hζ=-3n216-34φζ, Hζ=-3n216-34ζ, Hx,t=-3n216-34x-vt,x,t=-3n216-34x-vt, x,t=-3n216-34x-vtexp⁡iΨx-vt,$ (21)

where $Ψx,t=-kx+wt+φx,t.$

$qx,t=-3-163A016-34x-vtexp⁡i-kx+wt+1x-vt,$ (22)

$Re qx,t=1-1.74x-vtcos⁡-kx+wt+1x-vt,$ (23)

$Im qx,t=1-34x-vtsin⁡-kx+wt+1x-vt,$ (24)

Similarly, from Eqs. (7-10), another solutions is given by

$Hζ=-3n216-34φζ+1813φζ,$

and since $b>0$ , then

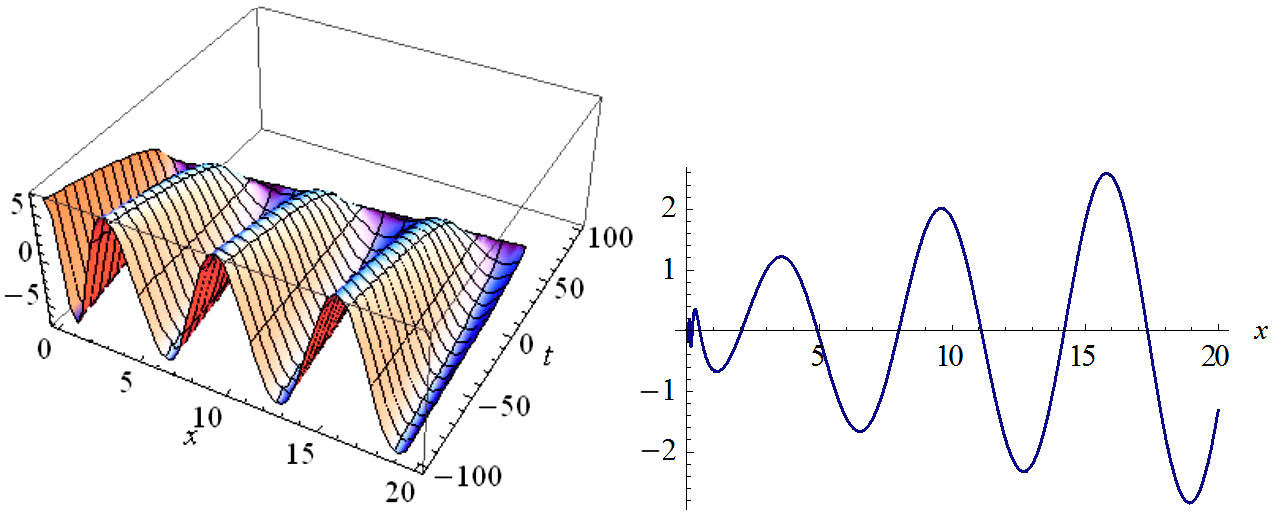
FIGURE 1 The plot of real part Eq. (23) in two and three dimensions with values: $n1=4A02$ , $n2=-16A0/3,$ $n3=2,$ $A1=-(i/2)(3/2)$ , $B1=0,$ $b=0$ .

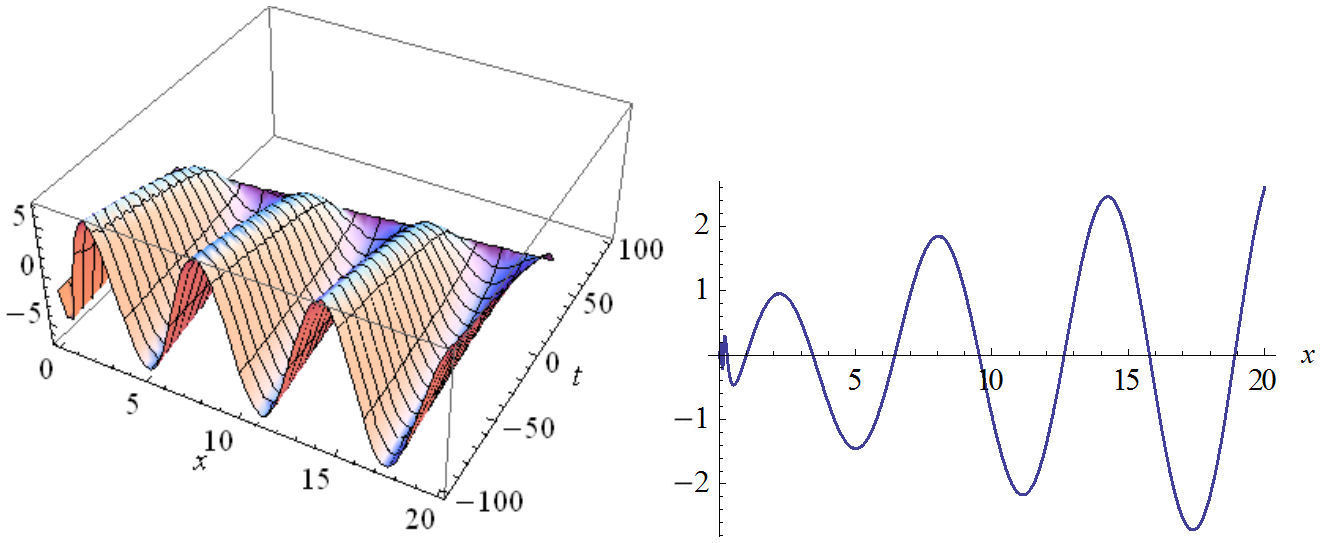
FIGURE 2 The plot of imaginary part Eq. (24) in two and three dimensions with values: $n1=4A02$ , $n2=-16A0/3,$ $n3=2,$ $A1=-(i/2)(3/2)$ , $B1=0,$ $b=0$ .

$Hx,t=-3n216-18313tan⁡7213x-vt+1872tan⁡7213x-vt,ux,t=-3n216-18313tan⁡7213x-vt+1872tan⁡7213x-vt1/2q1x,t=-3n216-18313tan⁡7213x-vt+1872tan⁡7213x-vt1/2exp⁡iΨx-vt,$ (25)

$Re q1x,t=-1.8-8.6tan⁡20{x-vt}+14tan⁡20{x-vt}0.5cos⁡-kx+wt+1x-vt,$ (26)

$Im q1x,t=-1.8-8.6tan⁡20{x-vt}+14tan⁡20{x-vt}0.5sin⁡-kx+wt+1x-vt$ (27)

$Hx,t=-3n216+18313cot⁡7213x-vt-1872cot⁡7213x-vt,ux,t=-3n216+18313cot⁡7213x-vt-1872cot⁡7213x-vt1/2, q2x,t=-3n216+18313cot⁡7213x-vt-1872cot⁡7213x-vt1/2exp⁡iΨx-vt.$ (28)

$Re q1x,t=-1.8-8.6cot⁡20{x-vt}+14cot⁡20{x-vt}0.5cos⁡-kx+wt+1x-vt,$ (29)

$Im q1x,t=-1.8-8.6cot⁡20{x-vt}+14cot⁡20{x-vt}0.5sin⁡-kx+wt+1x-vt,$ (30)

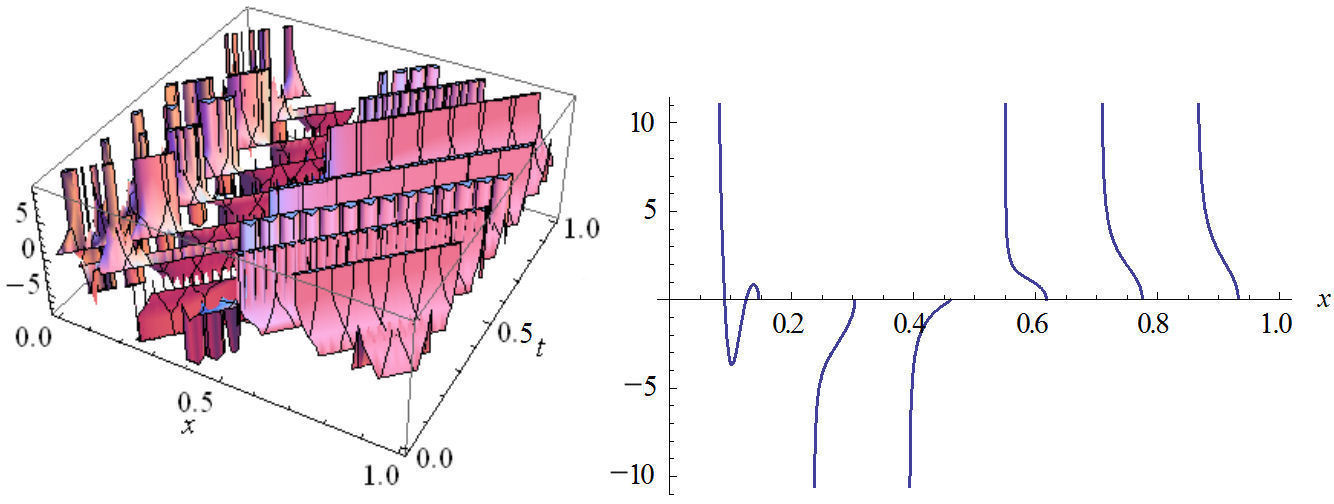
FIGURE 3 The plot of real part Eq. (26) in two and three dimensions with values: $n1=-44-8.3i$ , $n2=-9.8i$ , $n3=2$ , $A0=1.8i$ , $A1=0.6i$ , $B1=(6.9-10i)$ , $b=11.1-16.6i$ .

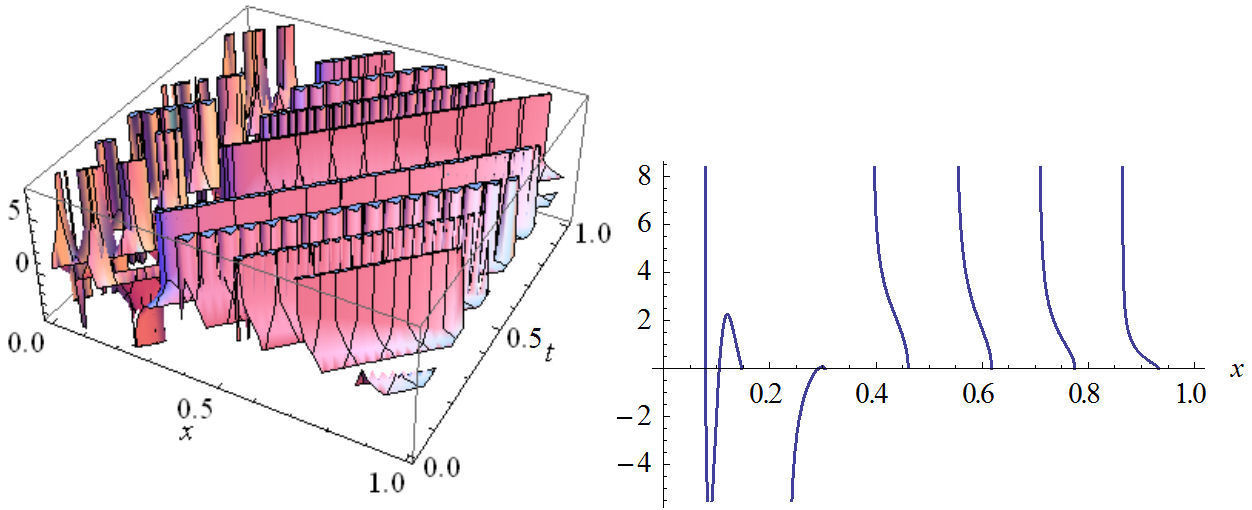
FIGURE 4 The plot of imaginary part Eq. (27) in two and three dimensions with values: $n1=-44-8.3i$ , $n2=-9.8i$ , $n3=2$ , $A0=1.8i$ , $A1=0.6i$ , $B1=(6.9-10i)$ , $b=11.1-16.6i$ .

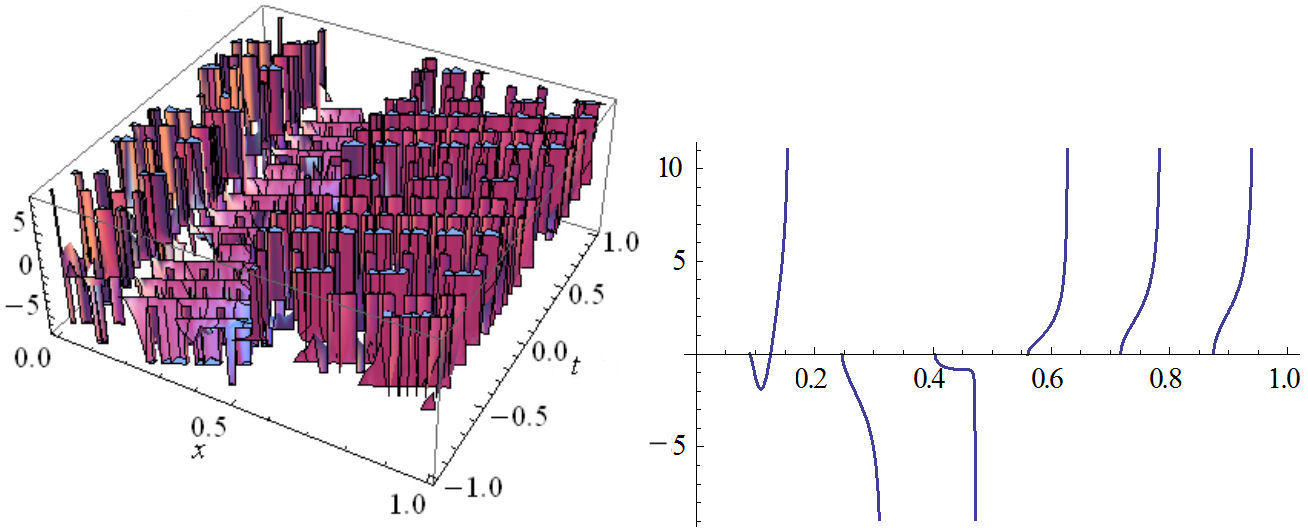
FIGURE 5 The plot of real part Eq. (29) in two and three dimensions with values: $n1=-44-8.3i$ , $n2=-9.8i$ , $n3=2$ , $A0=1.8i$ , $A1=0.6i$ , $B1=(6.9-10i)$ , $b=11.1-16.6i$ .

FIGURE 6 The plot of imaginary part Eq. (30) in two and three dimensions with values: $n1=-44-8.3i$ , $n2=-9.8i$ , $n3=2$ , $A0=1.8i$ , $A1=0.6i$ , $B1=(6.9-10i)$ , $b=11.1-16.6i$ .

3. The RBSub-ODE method

According to the RBSub-ODE method [²⁹^,³⁰] the suggested solution is

$u'=Au2-n+Bu+Cun,$ (31)

where $a,b,c,$ and $m$ are constants to be determined later. It is important to note that when $AC≠0$ and $n=0$ (31) is a Riccati equation. When $A≠0,$ $c=0,$ and $n≠1$ , (31) is a Bernoulli equation. By differentiating Eq. (31) once we get

$u''=AB3-nu2-n+A22-nu3-2n+nC2u2n-1+BCn+1un+2AC+B2u.$ (32)

Substituting the derivatives of $u$ into (31) yields an algebraic equation of by consider the symmetry of the right-hand item of (31) and setting equivalence for the highest power exponents of $u$ we can determine $m.$ Comparing the coefficients of $ui$ yields a set of algebraic equations that can be solved for $A$ , $B$ , and $C$ .

According to the obtained values of these constants and using the transformation $ζ=x-vt$ the RBSub-ODE equation admits the following solutions:

(1) When $n=1$ , the solution of Eq. (31) is,

$uζ=C1εA+B+Cζ.$ (33)

(2) When $n≠1,$ $B=0$ and $C=0$ , the solution of Eq. (31) is,

$uζ=An-1ζ+C11/1-n.$ (34)

(3) When $n≠1,$ $B≠0$ and $C=0$ , the solution of Eq. (31) is,

$uζ=-AB+C1εBn-1ζ1/n-1.$ (35)

(4) When $n≠1,$ $A≠0$ and B²- 4 AC < 0, the solution of Eq. (31) is,

$uζ=-B2A+4AC-B22Atan⁡1-n4AC-B22ζ+C11/1-n,$ (36)

$uζ=-B2A+4AC-B22Acot⁡1-n4AC-B22ζ+C11/1-n,$ (37)

(5) When $n≠1,$ $A≠0$ and B²- 4 AC > 0, the solution of Eq. (31) is,

$uζ=-B2A+B2-4AC2Acoth⁡1-nB2-4AC2ζ+C11/1-n,$ (38)

$uζ=-B2A+B2-4AC2Atanh⁡1-nB2-4AC2ζ+C11/1-n,$ (39)

(6) When $n≠1,$ $A≠0$ and B²- 4 AC = 0, the solution of Eq. (31) is,

$uζ=1An-1ζ+C1-B2A1/1-n,$ (40)

where $C1$ is an arbitrary constant.

Now we will apply the RBSub-ODE method for the equation mentioned above,

$2HH''-H'2+4n1H2+4n2H3+4n3H4=0,$ (41)

that can be rewritten according to the RBSub-ODE method as

$H'=AH2-n+BH+CHn.$

Hence,

$H''=3-nABH2-n+2-nA2H3-2n+nC2H2n-1+n+1BCHn+2AC+B2H,HH''=3-nABH3-n+2-nA2H4-2n+nC2H2n+n+1BCHn+1+2AC+B2H2,$ (42)

which we can substitute into Eq. (41) after taking $m=1$ we get

$23-nABH3-n+2-nA2H4-2n+nC2H2n+n+1BCHn+1+2AC+B2H2-AH2-n+BH+CHn2+4n1H2+4n2H3+4n3H4=0,$ (43)

which can be expressed as

$6ABH3+4A2H\cua+2BCH+4AC+2B2H2-AH2+BH+C2+4n1H2+4n2H3+4n3H4=0.$ (44)

Equating the coefficients of different powers of $H$ to zero, we get a simple system of algebraic equations,

$H4⇒3A2+4n3=0,H3⇒AB+n2=0,H2⇒2AC+B2+4n1=0,Constant⇒C=0.$ (45)

By solving this system of algebraic equations, we get,

$A=±-4n33, B=±n2-4n33, C=0.$ (46)

According to these obtained solutions and the constructed method we have the following cases:

(7) When $n≠1,$ $B≠0$ and $c=0$ , the solution becomes

$Hζ=4n33n2+C1e-Bζ,Hx,t=4n33n2+C1e-Bx-vt,Wx,t=4n33n2+C1e-Bx-vt-1/2, q3x,t=4n33n2+C1e-Bx-vt-1/2ei-kx+wt+θ,$ (47)

$Re q3x,t=4n33n2+C1e-Bx-vt-1/2cos⁡-kx+wt+1x-vt,$ (48)

$Im q3x,t=4n33n2+C1e-Bx-vt-1/2sin⁡-kx+wt+θ.$ (49)

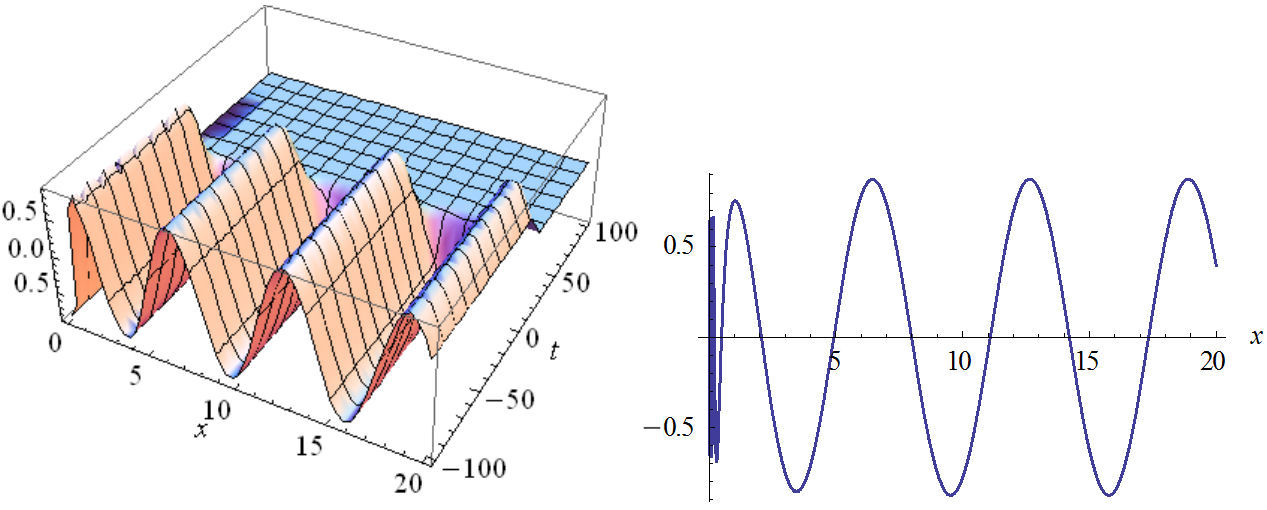
FIGURE 7 The plot of real part Eq. (48) in two and three dimensions with $n2=1$ , $n3=-1,$ $B=0.8,$ $C=0,$ $C1=1,$ $w=1,$ $v=1,$ $A=±1.2$ .

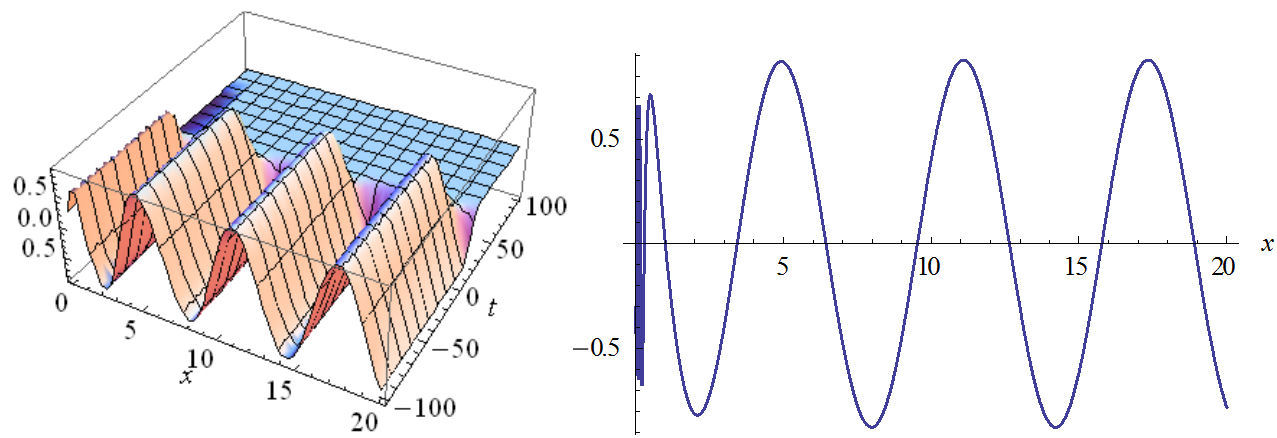
FIGURE 8 The plot of imaginary part Eq. (49) in two and three dimensions with values: n ₂ = 1, n ₃ = −1, B = 0.8, C = 0, C ₁ = 1, w = 1, v = 1, A = ±1.2.

(8) When $n≠1,$ $A≠0$ and B²- 4 AC < 0,

$uζ=4n36n2+9n22-16n32tan⁡3n224n32ζ+C1,$

and

$uζ=4n36n2+9n22-16n32cot⁡3n224n32ζ+C1,$

leading to

$ux,t=4n36n2+9n22-16n32tan⁡3n224n32x-vt+C1,$

and

$ux,t=4n36n2+9n22-16n32cot⁡3n224n32x-vt+C1.$

Thus,

$wx,t=4n36n2+9n22-16n32tan⁡3n224n32x-vt+C1-1/2,$

and

$wx,t=4n36n2+9n22-16n32cot⁡3n224n32x-vt+C1-1/2.$

Hence,

$q4x,t=4n36n2+9n22-16n32tan⁡3n224n32x-vt+C1-1/2ei-kx+wt+θ,$ (50)

$Re q4x,t=0.6+0.75tan⁡0.4{x-vt+C1}-0.5cos⁡-kx+wt+1x-vt,$ (51)

$Im q4x,t=0.6+0.75tan⁡0.4{x-vt+C1}-0.5sin⁡-kx+wt+1x-vt,$ (52)

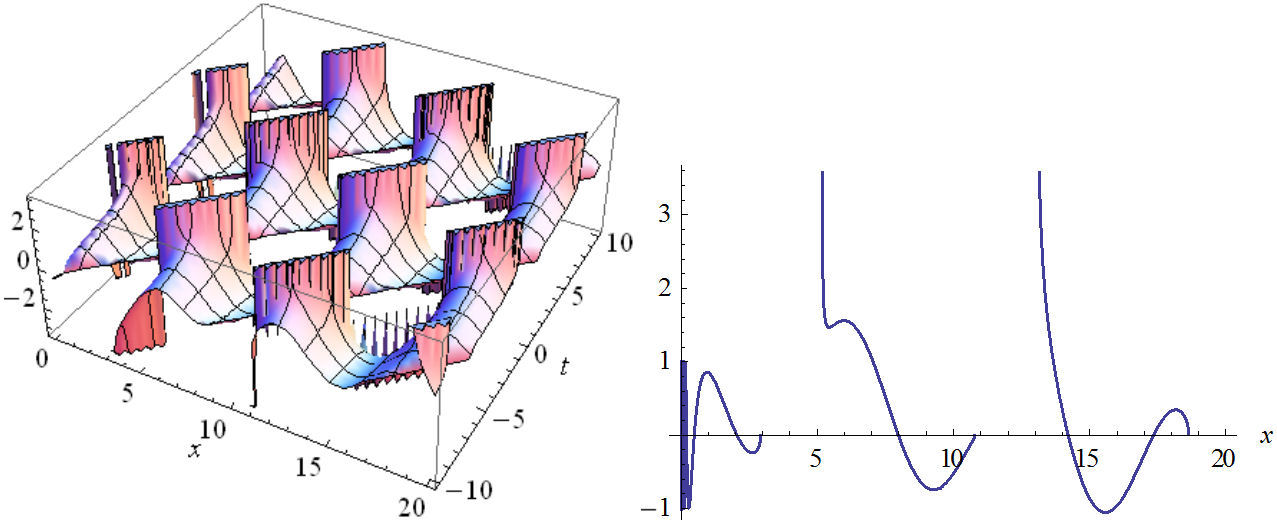
FIGURE 9 The plot of real part Eq. (51) in two and three dimensions with n ₂ = 1, n ₃ = 1, B = 0.8, C = 0, C ₁ = 1, w = 1, v = 1, A = ±1.2.

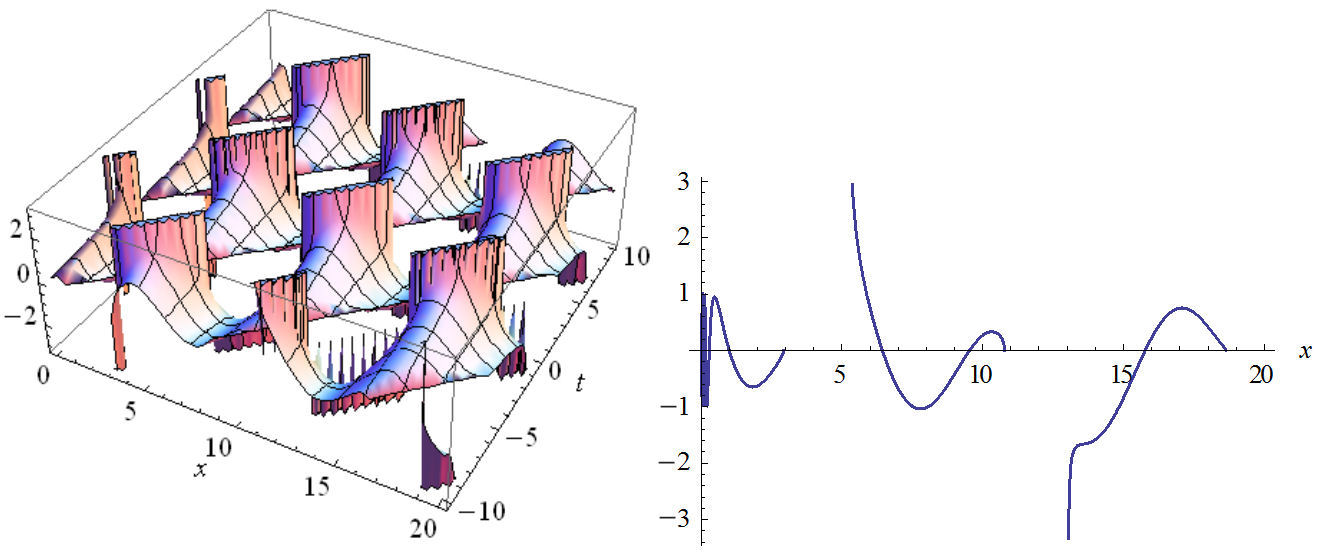
FIGURE 10 The plot of imaginary part Eq. (52) in two and three dimensions with values: n ₂ = 1, n ₃ = 1, B = 0.8, C = 0, C ₁ = 1, w = 1, v = 1, A = ±1.2.

And

$q5x,t=4n36n2+9n22-16n32cot⁡3n224n32x-vt+C1-1/2ei-kx+wt+θ,$ (53)

$Re q5x,t=0.6+0.75cot⁡0.4{x-vt+C1}-0.5cos⁡-kx+wt+1x-vt,$ (54)

$Im q5x,t=0.6+0.75cot⁡0.4{x-vt+C1}-0.5sin⁡-kx+wt+1x-vt.$ (55)

(9) When $n≠1,$ $A≠0$ and B 2 − 4 AC > 0,

$uζ=2n33n2-2n33n2coth⁡n22-34n3ζ+C1,$

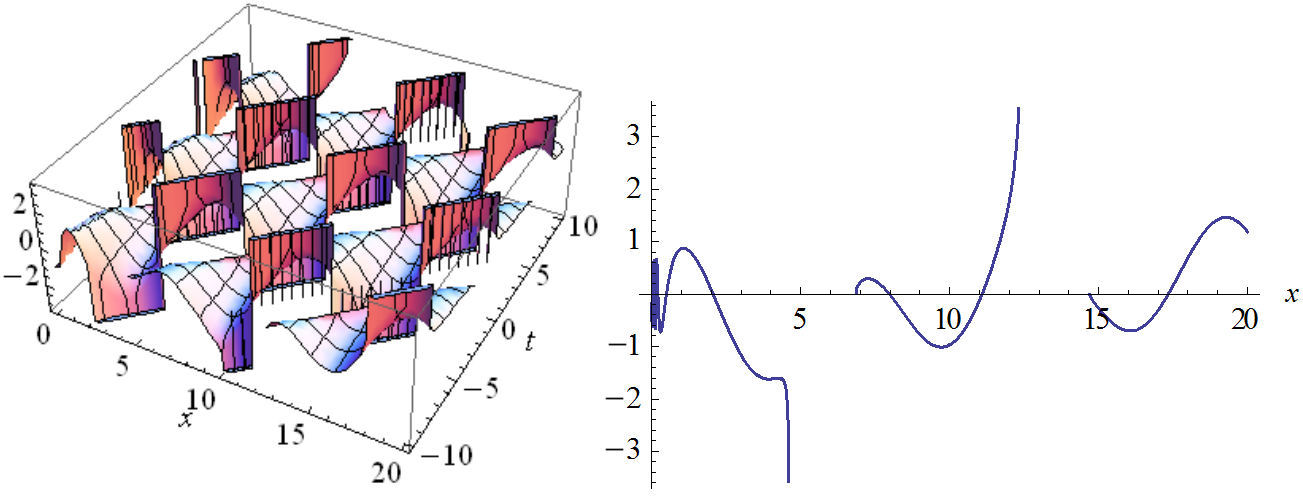
FIGURE 11 The plot of real part Eq. (54) in two and three dimensions with n₂ = 1, n₃ = 1, B = 0.8, C = 0, C₁ = 1, w = 1, v = 1, A = ±1.2.

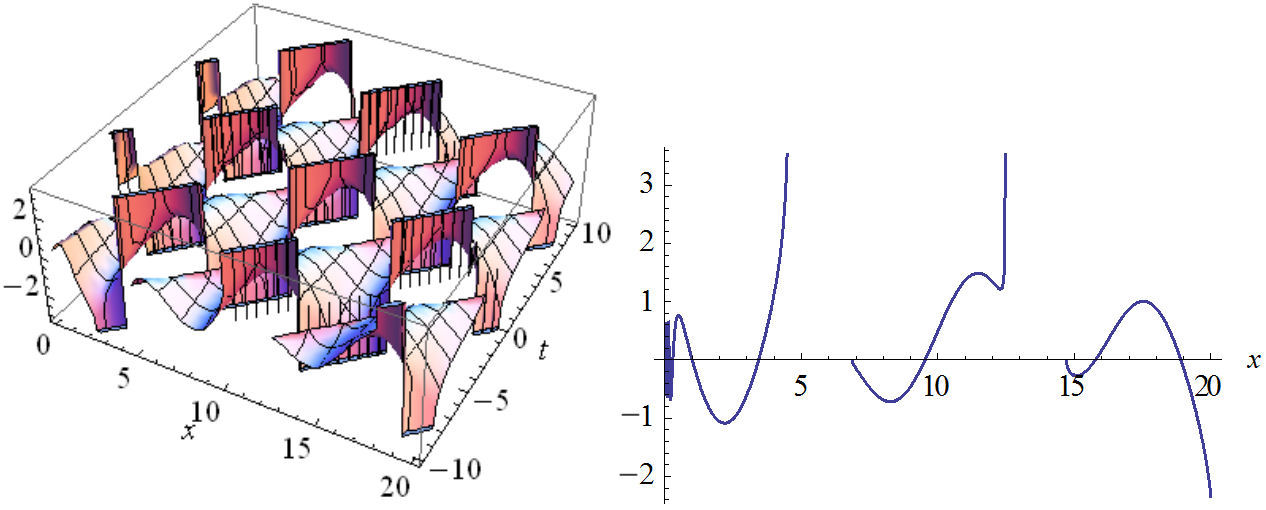
FIGURE 12 The plot of imaginary part Eq. (55) in two and three dimensions with values: n₂ = 1, n₃ = 1, B = 0.8, C = 0, C₁ = 1, w = 1, v = 1, A = ±1.2.

and

$uζ=2n33n2-2n33n2tanh⁡n22-34n3ζ+C1, uζ=2n33n2-2n33n2coth⁡n22-34n3x-vt+C1,$

leading to

$ux,t=2n33n2-2n33n2tanh⁡n22-34n3x-vt+C1.$

Thus

$wx,t=2n33n2-2n33n2coth⁡n22-34n3x-vt+C1-1/2,$

and

$wx,t=2n33n2-2n33n2tanh⁡n22-34n3x-vt+C1-1/2.$

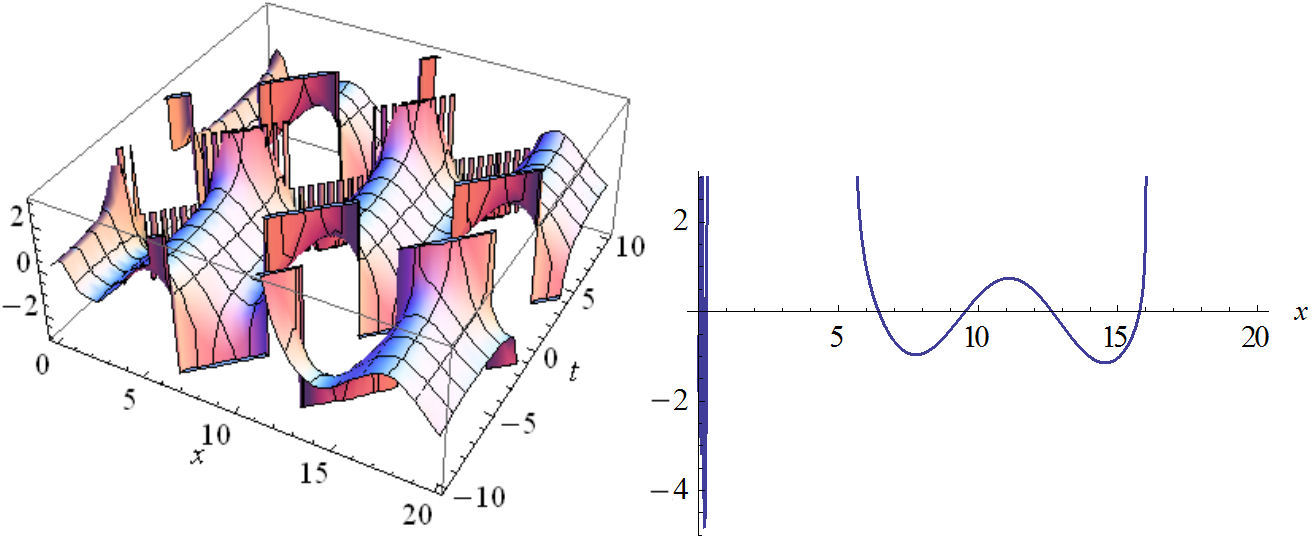
FIGURE 13 The plot of real part Eq. (57) in two and three dimensions with n₂ = 1, n₃ = 1, B = 0.8, C = 0, C₁ = 1, w = 1, v = 1, A = ±1.2.

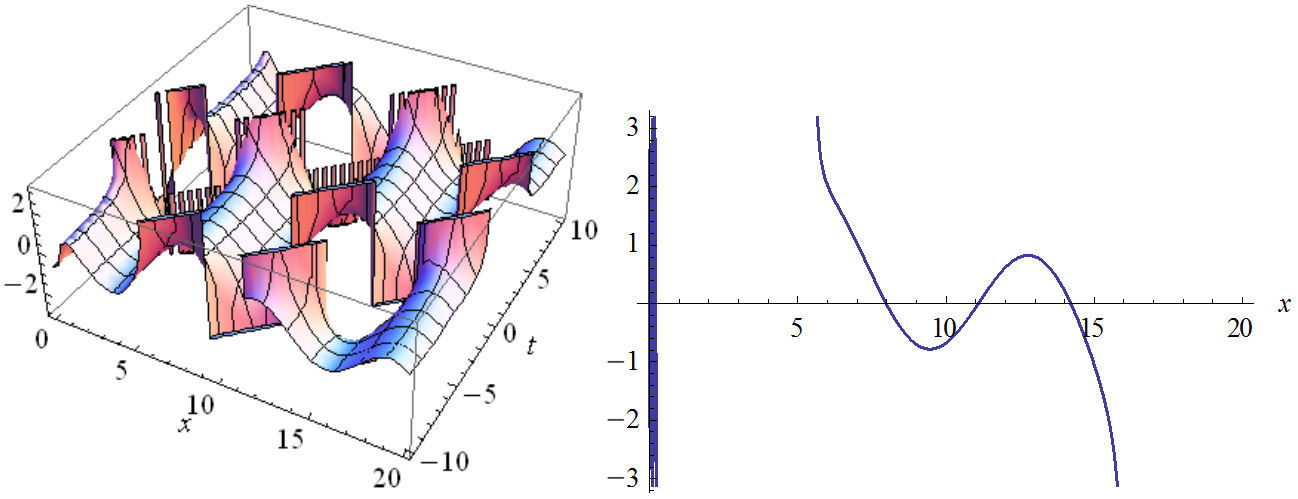
FIGURE 14 The plot of imaginary part Eq. (58) in two and three dimensions with values: n₂ = 1, n₃ = 1, B = 0.8, C = 0, C₁ = 1, w = 1, v = 1, A = ±1.2.

Hence,

$wx,t=2n33n2-2n33n2tanh⁡n22-34n3x-vt+C1-1/2,q6x,t=2n33n2-2n33n2tanh⁡n22-34n3x-vt+C1-1/2ei-kx+wt+θ,$ (56)

$Re q6x,t=0.6-1.2sin⁡0.4{x-vt+C1}-1/2sin⁡-kx+wt+1x-vt,$ (57)

$Im q6x,t=0.6-1.2sin⁡0.4{x-vt+C1}-1/2cos⁡-kx+wt+1x-vt.$ (58)

By the same manner we can easily plot the last equation,

$q7x,t=2n33n2-2n33n2coth⁡n22-34n3x-vt+C1-1/2ei-kx+wt+θ.$

4. Conclusion

In this work, using the solution of the auxiliary (4) in the framework of the METF method, we have obtained the exact solutions for the perturbed GI equation. A new technique, following the RBSub-ODE method, reduces the number of calculations in a significant manner while the treatment of the failure of the balance rule is successfully used to get new optical solitons of the perturbed GI equation. We also conclude that these techniques are effective and convenient methods and can be applied to other NLPDEs.

References

1. C. Gu, Soliton Theory and Its Applications (Springer-Verlag, Berlin, 1995), https://doi.org/10.1007/978-3-662-03102-5. [ Links ]

2. N. A. Kudryashov, On types of nonlinear nonintegrable equations with exact solutions, Physics Letters A. 155 (1991) 269. https://doi.org/10.1016/0375-9601(91)90481-M. [ Links ]

3. H. Zhang, Extended Jacobi elliptic function expansion method and its applications, Commun. Nonlinear Sci. Numer. Simul. 12 (2007) 627, https://doi.org/10.1016/j.cnsns.2005.08.003. [ Links ]

4. L. Kaur and R. K. Gupta, Some invariant solutions of field equations with axial symmetry for empty space containing an electrostatic field, Appl. Math. Comput. 231 (2014) 560, https://doi.org/10.1016/j.amc.2013.12.120. [ Links ]

5. B. Sun and A.-M. Wazwaz, General high-order breathers and rogue waves in the (3+1)-dimensional KP-Boussinesq equation, Commun. Nonlinear Sci. Numer. Simul. 64 (2018) 1, https://doi.org/10.1016/j.cnsns.2018.04.005. [ Links ]

6. A.-M. Wazwaz, Painlevé analysis for a new integrable equation combining the modified Calogero-Bogoyavlenskii-Schiff (MCBS) equation with its negative-order form, Nonlinear Dyn. 91 (2018) 877, https://doi.org/10.1007/s11071-017-3916-0. [ Links ]

7. L. Kaur and A. M. Wazwaz, Similarity solutions of field equations with an electromagnetic stress tensor as source, Rom. Rep. Phys. 70 (2018) 114. [ Links ]

8. L. Kaur and A.-M. Wazwaz, Dynamical analysis of lump solutions for (3+1) dimensional generalized KP-Boussinesq equation and its dimensionally reduced equations, Phys. Scr. 93 (2018) 075203, https://doi.org/10.1088/1402-4896/aac8b8. [ Links ]

9. A. J. M. Jawad, New Exact Solutions of Nonlinear Partial Differential Equations Using Tan-Cot Function Method, Stud. Math. Sci. 5 (2012) 13, https://doi.org/10.3968/j.sms.1923845220120502.1452. [ Links ]

10. B. Ghanbari and J. F. Gómez-Aguilar, The generalized exponential rational function method for Radhakrishnan-Kundu-Lakshmanan equation with β- conformable time derivative, Rev. Mex. Fis. 65 (2019) 503, https://doi.org/10.31349/RevMexFis.65.503. [ Links ]

11. O. A. Ilhan and J. Manafian, Analytical treatment in optical metamaterials with anti-cubic law of nonlinearity by improved exp(-Ω(η))-expansion method and extended sinh-Gordon equation expansion method, Rev. Mex. Fis. 65 (2019) 568, https://doi.org/10.31349/RevMexFis.65.658. [ Links ]

12. Senol, New analytical solutions of fractional symmetric regularized-longwave equation, Rev. Mex. Fis. 66 (2020) 297, https://doi.org/10.31349/RevMexFis.66.297. [ Links ]

13. E. H. M. Zahran, Exact Traveling Wave Solutions of Nano-Ionic Solitons and Nano-Ionic Current of MTs Using the exp(-ϕξ)-Expansion Method, Adv. Nanopart. 4 (2015) 25, https://doi.org/10.4236/anp.2015.42004. [ Links ]

14. M. S. M. Shehata, The exp(-j(x)) Method and Its Applications for Solving Some Nonlinear Evolution Equations in Mathematical Physics, Am. J. Comput. Math. 5 (2015) 468, https://doi.org/ 10.4236/ajcm.2015.54041. [ Links ]

15. M. Mirzazadeh, M. Eslami, and A. Biswas, Soliton solutions of the generalized Klein-Gordon equation by using (G'/G)-expansion method, Comput. Appl. Math. 3 (2014) 831, https://doi.org/10.1007/s40314-013-0098-3. [ Links ]

16. E H Zahran and M. M. Khater Jokull, Exact solutions to some nonlinear evolution equations by the (G'/G)-expansion method, Journal 64 (2014) 226. [ Links ]

17. H. Rezazadeh, New solitons solutions of the complex Ginzburg-Landau equation with Kerr law nonlinearity, Optik 167 (2018) 218, https://doi.org/10.1016/j.ijleo.2018.04.026. [ Links ]

18. H. Rezazadeh et al., New optical solitons of nonlinear conformable fractional Schrödinger-Hirota equation, Optik 172 (2018) 545, https://doi.org/10.1016/j.ijleo.2018.06.111. [ Links ]

19. M. Eslami and H. Rezazadeh, The first integral method for Wu-Zhang system with conformable time-fractional derivative, Calcolo 53 (2016) 475, https://doi.org/10.1007/s10092-015-0158-8. [ Links ]

20. M. Eslami andM. Mirzazadeh , First integral method to look for exact solutions of a variety of Boussinesq-like equations, Ocean Eng. 83 (2014) 133, https://doi.org/10.1016/j.oceaneng.2014.02.026. [ Links ]

21. E. H. M. Zahran and M. M. A. Khater, Exact Traveling Wave Solutions for the System of Shallow Water Wave Equations and Modified Liouville Equation Using Extended Jacobian Elliptic Function Expansion Method, Am. J. Comput. Math. 4 (2014) 455, https://doi.org/10.4236/ajcm.2014.45038. [ Links ]

22. M. S. M. Shehata, Extended Jacobian Elliptic Function Expansion Method and its Applications for Solving some Nonlinear Evolution Equations in Mathematical Physics, Int. J. Comput. Appl. 109 (2015) 1. [ Links ]

23. M. Eslami andM. Mirzazadeh , Optical solitons with Biswas-Milovic equation for power law and dual-power law nonlinearities, Nonlinear Dyn. 83 (2016) 731, https://doi.org/10.1007/s11071-015-2361-1. [ Links ]

24. M. Eslami , Trial solution technique to chiral nonlinear Schrödinger’s equation in (1+2)-dimensions, Nonlinear Dyn. 85 (2016) 813, https://doi.org/10.1007/s11071-016-2724-2. [ Links ]

25. H. Rezazadeh et al., Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Ricatti equation method, Opt. Quantum Electron. 50 (2018) 150, https://doi.org/10.1007/s11082-018-1416-1. [ Links ]

26. F. S. Khodadad, F. Nazari, M. Eslami , andH. Rezazadeh , Soliton solutions of the conformable fractional Zakharov-Kuznetsov equation with dual-powe law nonlinearity, Opt. Quantum Electron. 49 (2017) 384, https://doi.org/10.1007/s11082-017-1225-y. [ Links ]

27. E. H. M. Zahran and M. M. A. Khaater, Modified extended tanh-function method and its applications to the Bogoyavlenskii equation, Appl. Math. Model. 40 (2016) 1769, https://doi.org/10.1016/j.apm.2015.08.018. [ Links ]

28. M. M. A. Khater, D. Lu, and E. H. M. Zahran, Solitary Wave Solutions of the Benjamin-Bona-Mahoney-Burgers Equation with Dual Power-Law Nonlinearity, Appl. Math. Inf. Sci. 11 (2017) 1347, https://doi.org/10.18576/amis/110511. [ Links ]

29. X.-F. Yang, Z.-C. Deng, and Y. Wei, A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its applications, Adv. Differ. Equ. 2015 (2015) 117, https://doi.org/10.1186/s13662-015-0452-4. [ Links ]

30. M. S. M. Shehata, A new solitary wave solution of the perturbed nonlinear Schrödinger equation using a Riccati-Bernoulli Sub-ODE method, Int. J. Phys. Sci. 11 (2016) 80, https://doi.org/10.5897/IJPS2015.4442. [ Links ]

31. V. S. Gerdjikov and M. I. Ivanov, The quadratic bundle of general form and the nonlinear evolution equations. II. Hierarchies of Hamiltonian structures, Bulgarian J. Phys. 10 (1983) 130. [ Links ]

32. E. Fan, Integrable evolution systems based on Gerdjikov-Ivanov equations, bi-Hamiltonian structure, finite-dimensional integrable systems and N-fold Darboux transformation, J. Math. Phys. 41 (2000) 7769, https://doi.org/10.1063/1.1314895. [ Links ]

33. H. H. Dai and E. G. Fan, Variable separation and algebro-geometric solutions of the Gerdjikov-Ivanov equation, Chaos Solitons Fractals 22 (2004) 93, https://doi.org/10.1016/j.chaos.2003.12.059. [ Links ]

34. X. Guo, Two expanding integrable systems of the GI soliton hierarchy and a generalized GI hierarchy with self-consistent sources as well as its extension form, Commun. Nonlinear Sci. Numer. Simul. 14 (2009) 4065, https://doi.org/10.1016/j.cnsns.2009.02.018. [ Links ]

35. B. He and Q. Meng, Bifurcations and new exact travelling wave solutions for the Gerdjikov-Ivanov equation, Commun. Nonlinear Sci. Numer. Simul. 15 (2010) 1783, https://doi.org/10.1016/j.cnsns.2009.07.019. [ Links ]

36. X. Lü et al., Envelope bright- and dark-soliton solutions for the Gerdjikov-Ivanov model, Nonlinear Dyn. 82 (2015) 1211, https://doi.org/10.1007/s11071-015-2227-6. [ Links ]

37. H. Yilmaz, Exact solutions of the Gerdjikov-Ivanov equation using Darboux transformations, J. Nonlinear Math. Phys. 22 (2014) 32, https://doi.org/10.1080/14029251.2015.996438. [ Links ]

38. E. Fan, Darboux transformation and soliton-like solutions for the Gerdjikov- Ivanov equation, J. Phys. A 33 (2000) 6925, https://doi.org/10.1088/0305-4470/33/39/308. [ Links ]

39. C. Rogers and K. W. Chow, Localized pulses for the quintic derivative nonlinear equation on a continuous-wave background, Phys. Rev. E 86 (2012) 037601, https://doi.org/10.1103/PhysRevE.86.037601. [ Links ]

40. J. Manafian and M. Lakestani, Optical soliton solutions for the Gerdjikov- Ivanov model via tan(ϕ/2)-expansion method, Optik 127 (2016) 9603, https://doi.org/10.1016/j.ijleo.2016.07.032. [ Links ]

41. A. Biswas , Y. Yildirim, E. Yasar, and M. M. Babatin, Conservation laws for Gerdjikov-Ivanov equation in nonlinear fiber optics and PCF, Optik 148 (2017) 209, https://doi.org/10.1016/j.ijleo.2017.08.094. [ Links ]

42. H. Triki, R. T. Alqahtani, Q. Zhou, andA. Biswas , New envelope solitons for Gerdjikov-Ivanov model in nonlinear fiber optics, Superlattices Microstruct. 111 (2017) 326, https://doi.org/10.1016/j.spmi.2017.06.046. [ Links ]

43. J.-B. Zhang, Y.-Y. Gongye, and S.-T. Chen, Soliton Solutions to the Coupled Gerdjikov-Ivanov Equation with Rogue-Wave-Like Phenomena, Chin. Phys. Lett. 34 (2017) 090201, https://doi.org/10.1088/0256-307X/34/9/090201. [ Links ]

44. A. Biswas et al., ptical soliton perturbation with full nonlinearity for Gerdjikov-Ivanov equation by trial equation method, Optik 157 (2018) 1214, https://doi.org/10.1016/j.ijleo.2017.12.099. [ Links ]

45. J. Manafian and M. Lakestani, Lump-type solutions and interaction phenomenon to the bidirectional Sawada-Kotera equation, Pramana 92 (2019) 41, https://doi.org/10.1007/s12043-018-1700-4. [ Links ]

46. J. Manafian, Novel solitary wave solutions for the (3+1)-dimensional extended Jimbo-Miwa equations, Comput. Math. Appl. 76 (2018) 1246, https://doi.org/10.1016/j.camwa.2018.06.018. [ Links ]

47. J. Manafian, B. Mohammadi-Ivatloo, and M. Abapour, Lump-type solutions and interatction phenomenon to the (2+1)-dimensional Breaking Soliton equation, Appl. Math. Comput. 356 (2019) 13, https://doi.org/10.1016/j.amc.2019.03.016. [ Links ]

48. M. Dehghan, J. Manafian , and A. Saadatmandi, Solving nonlinear fractional partial differential equations using the homotopy analysis method, Numer. Methods Partial Differ. Equ. 26 (2010) 448, https://doi.org/10.1002/num.20460. [ Links ]

49. L. Kaur and A.-M. Wazwaz, Optical solitons for perturbed Gerdjikov-Ivanov equation, Optik 174 (2018) 447, https://doi.org/10.1016/j.ijleo.2018.08.072. [ Links ]

Received: May 10, 2020; Accepted: September 30, 2020

This is an open-access article distributed under the terms of the Creative Commons Attribution License