1.Introduction

A brane world corresponds to a 4-dimensional hypersurface embedded in a high dimensional bulk, on which gravity is localized . In the most general case, the 4-dimensional sector can be generated by a scalar domain wall interpolating between two asymptotic Anti de-Sitter (AdS) vacuums, with different cosmological constants at each side of the wall, i.e., a solution to the coupled Einstein-Klein Gordon system with a potential with a spontaneously broken discrete symmetry ^3-7. The gravity fluctuations of this spacetime depend on the wall’s thickness and are characterized by both a zero -mode localized on the wall and a spectrum of massive states propagating freely. In the thin- wall limit (6),(12), the gravitational potential can be calculated, and Newtonian gravity is recovered on the 4-dimensional sector of the scenario.

To localize the matter field, a Yukawa coupling between the bulk fermions and the scalar field of the wall is required; however, in this case, only one chiral massless state (left or right) is localized, while the other is repelled by the gravitational field of the wall (13)-(26). Remarkably, we determined that the minimum bound of the Yukawa constant, obtained from conditions of normalization, is not sufficient to confine the fermion in 4-dimensions with maximum probability on the scalar wall.

On the other hand, it is well known that in the absence of Z ₂ symmetry, the gravitational field of the brane shifts the fermion toward the 5-dimensional sector with greater curvature ²². Here, we show that another shift-like effect exists, regardless of the reflection symmetry of the scenario. For some values of the Yukawa coupling constant, the chiral fermion can be shifted simultaneously at each side of the wall, i.e., the bound state exhibits two relative maximums close to the wall and hence the probability of finding the particle is greater around the wall rather than on it.

To rule out the relationship between the symmetry of the scenario and the fermion’s migration, we consider two models differentiated by their reflection symmetry. The first one corresponds to the member with Z ₂ symmetry of a family of asymmetric domain walls ⁴, while the second one is an intrinsically asymmetric wall family ^9,21. In both cases, when the fermion satisfies the normalization condition and it is distributed (centered) around the wall, there are obtained two peaks at each side of the wall, in the probability profile of the fermion. For the other cases, where only the normalization condition is satisfied, the fermion is always confined outside the wall.

2.Set-up

Consider the coupled Einstein scalar field system in 5-dimensions (latin index a,b= 0, ⋯, 4; greek index μ,ν= 0, ⋯, 3)

where the metric is given by

which corresponds to a spacetime with plane parallel symmetry whose energy density is determined by

Here and in the other sections, prime denotes the derivative concerning y.

We are interested in AdS₅ domain wall solutions, scenarios for which geometry is determined by a scalar field ϕ interpolating between the negative minima of the potential V(ϕ). It is well known that the full spectrum of the gravity fluctuations of these scenarios is characterized by a zero -mode localized on the wall, ψ _g ∼e ^2Ay , and a continuum of massive modes propagating freely through the whole 5-dimensional bulk; see ⁹for details.

The chiral massless fermions can also be localized on the wall by a Yukawa coupling between the bulk fermions and the scalar field, λΨ¯ϕΨ. To evidence this, the Dirac equation for the 5-dimensional spinor in the background ([metric]) must be considered

To obtain the coordinates representation of the motion equation, it is common to rewrite Ψ(x,y) in terms of its chiral components left (L) and right (R), and factor its spatial degrees of freedom, as shown below

Where ψRL(x)≡±γ5ψRL(x), which satisfies the massless 4-dimensional Dirac equation

Thus, for ψRL(y) we have

for which

For a domain wall solution, e ^A is an integrable and asymptotically vanishing function, such that, e ^−A ∼e ^k|y| as |ky|≫1, with k=|Λ|/6, i.e., gravitation produces a repulsive effect on fermions. Hence, for the appropriate values of λ one of the ψRL can be normalized. In particular, for ψ _L in the large y limit, it is possible to see that

where ϕ(y= ±∞) = ± ϕ ₀ has been considered. Therefore

to cancel the repulsive effect generated by gravity.

The previous restriction for the Yukawa coupling is a necessary condition, but not sufficient to ensure the confinement of ψ _L on the wall. For some values of λ, we found solutions for ψ _L with two peaks at each side of the wall, generated by the gravitational competition between the geometry of the spacetime and the Yukawa interaction.

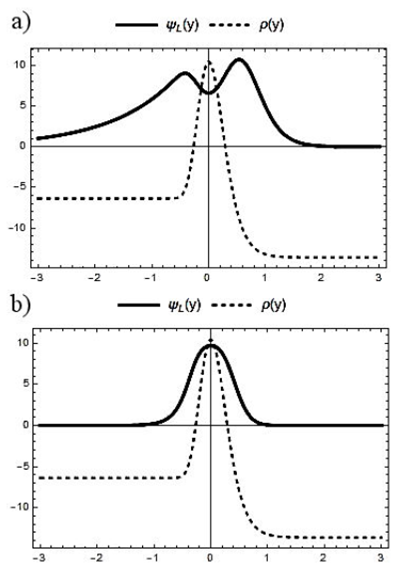
Let λ ₁ be the Yukawa critical constant from which ([hs]) is normalizable. Moreover, let λ ₂ be the Yukawa threshold from which the maximum of ([hs]) is on the wall (λ ₂ >λ ₁ ). Then, for λ<λ ₁ , the fermion is expelled from the thick brane by the gravitational field of the wall; while for λ>λ ₂ the fermion is localized on the wall. On the other hand, the sector λ ₁ <λ<λ ₂ corresponds to a bounded probability distribution with three critical points: a pair of maximums around the wall and a minimum on it. So, the chiral zero -mode of the matter fields is repelled by the thick brane and keeps orbiting around it.

The critical bound λ ₂ can be determined by a saddle point evaluation of (8). By assuming that ψ _L is peaked near the brane, y= 0, and that ψ _L ^′(0)=0 and ψ _L ^′′(0)<0, the following is obtained

Therefore, to preserve it as a real amount, the following is required

Now, to determinate the hierarchy between λ ₁ and λ ₂ , we will consider two specific solutions to the Einstein-Klein Gordon system (1), differentiated by the reflection symmetry of each scenario.

3.Symmetric walls

A solution to the coupled system (1) is given by

and

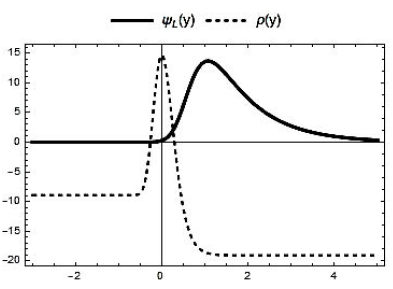
This solution was obtained in ⁴ and corresponds to a two-parameter domain wall interpolating asymptotically between two AdS₅ spacetime, with a cosmological constant given by Λ= −6α ² . Also, it is well known that the zero mode of gravity fluctuations is normalizable, and hence standard gravitation can be recovered in 4-dimensions.

Concerning to the massless fermions, from (8)

where Li_n is the polylogarithm function of order n given by

and from (10) and (12) we find

and

respectively.

Figure 1 shows the fermions profile for some values of λ. We observed that for λ>λ ₂ , ψ _L is normalizable, with maximum probability on the wall. On the other hand, if λ ₁ <λ<λ ₂ , a change occurs in the behavior of ψ _L ; in this case, the competition between gravitational interaction and Yukawa coupling divides the maximum of the profile into two maximums around the wall; i.e., the fermions prefer to orbit around the structure.

FIGURE 1 a) Massless fermion ψ _L and energy density p for λ ₁ <λ<λ ₂ and b) <λ<λ ₂ . 

4.Asymmetric walls

Before considering a thick domain wall with different cosmological constants at each side of the wall, Λ ₊ and Λ ₋ , it is convenient to estimate the asymptotic behavior of ψ _L in this scenario, i.e.,

where ϕ(y= ±∞) =ϕ _± and k±=|Λ±|/6 have been considered.

Obtain a normalizable solution for ψ _L , from (20) reads

Thus, two critical Yukawa constants associated with Λ _± are obtained, which are the result of the lack of Z ₂ symmetry.

Now, suppose that λ ₁₋ >λ ₁₊ and that λ ₁₋ >λ ₂ >λ ₁₊ . In this case, although λ ₂ is greater than one of the asymptotic constants, the migratory effect may not be present because λ ₂ <λ ₁₋ . On the other hand, there is the possibility that λ ₂ >λ ₁₋ , and even though the fermion is normalizable, it is more likely to orbit around the wall. To analyze this, let us consider one specific solution for the domain wall.

An asymmetric solution is determined by

where α and δ are positive constants and Ei is the exponential integral given by

The scalar field and potential for this scenario are

and

This solution was reported in and it corresponds to a two-parameter family of plane symmetric static domain walls without Z ₂ symmetry. The scalar field interpolates between two asymptotic vacua, ϕ ₋ = −ϵ for y< 0 and ϕ ₊ =ϕ ₀ −ϵ for y> 0, with different cosmological constants

Now, Eq. (8) provides that

Notice that, constants ϵ and β fix the asymptotic values of the scalar field and the cosmological constants, in such a way that, neither for the fermion nor for the graviton it is possible to find normalizable solutions as ϵ=β= 0 because ϕ ₋ =Λ ₋ = 0.

Now, to simplify we will consider the case β= 3α/e ² , where the wall is centered in y= 0, without loss of generality. However, the location of the fermion is shifted concerning the brane. To demonstrate this, let us calculate ψ _L near y= 0,

where

Thus, the wave function of the fermion is centered at y ₀ with a width given by eδ/(λϕ0-8α)α. The fermion’s shift was verified numerically beyond the approximation αy/δ≪ 1, and the results are shown in Fig. 2.

FIGURE 2 Massless fermion ψ _L shifted outside of energy density ,λ for ¸ λ > ¸ λ₂. 

Unlike in this article, the shift has previously been used to locate fermions on the wall: in ²⁷ where the spacetime is flat with an orbifold geometry ℝ⁴×S¹; and in ²², where the 5-dimensional spacetime is generated by a static double domain wall, in order to have the graviton and the fermion in different sub-walls.

For a scenario generated by a single wall with one non-compact extra dimension, shifting the fermion does not favor the creation of a brane world, since the maximum of probability is not on the wall. Therefore, in agreement with (29), ϵ=ϕ ₀ /e is required to center the fermion on the wall, and under this circumstance, it is possible to evaluate the migratory effect.

From (21) and (12), the following is obtained

and

in such a way that λ ₂ >λ ₁₋ >λ ₁₊ .

In Fig. 3, we plot the zero-mode fermion for some values of λ. For the migratory sector, λ ₁₊ <λ<λ ₂ , we can see two interfaces associated with the bounded state of ψ _L . The difference in the amplitude of the peaks is generated by the gravitational repulsion applied on the fermions, which expels them towards the region of the greater curvature. For λ>λ ₂ the probability’s maximum is in y= 0, and therefore, ψ _L is confined on the wall.

FIGURE 3 a) Fermion zero mode ψ _L and energy density p for ¸ λ ₁ < ¸ λ < ¸ λ ₂ and b) ¸ λ > λ ₂ . 

5.Discussion

The Yukawa coupling counteracts the repulsion exerted on the fermions by the gravitation of the wall, such that, utilizing a critical value of the Yukawa constant λ>λ ₁ (obtained by asymptotic analysis of the wave function), ensures the normalization of one of the chiral states. However, we found a range of values for the Yukawa constant, λ ₁ <λ<λ ₂ (by the Laplace method), where the fermion is in a normalizable state orbiting around the wall.

We calculated the Yukawa bounds, λ ₁ and λ ₂ , in two scenarios generated by a thick domain wall with or without reflection symmetry.

On the domain wall solution with reflection symmetry , A(y) and ϕ(y), the chiral massless fermion ψ _L is normalizable around the wall. On the other hand, the symmetric wall is part of a family of asymmetric solutions where A(y)→A(y)+βy and ϕ(y)→ϕ(y)−ϵ , and where the zero-mode of the fermion is determined by

the fermion is shifted from the wall by the term e ^−2βy . Therefore, it is not possible to evaluate the migratory effect on another member of the family of solutions, different than the Z ₂ -limit case: (β,ϵ)→(0, 0).

To evaluate the migratory effect on a scenario without Z ₂ symmetry, an intrinsically asymmetric domain wall , A(y) and ϕ(y), is required. This scenario is also a member of a two-parameter family, A(y)+βy and ϕ(y)−ϵ, but without the Z ₂ -limit, and to ensure that ψ _L (y) is centered in the maximum of ρ(y), β= 3α/e ² and ϵ=ϕ ₀ /e must be utilized.

In both cases the constraints imposed on the fermion to get it on the wall, lead to a hierarchy between λ ₂ and λ ₁ , such that, regardless of the scenario’s symmetry, the migratory effect could be present.