Articles

 

Saline intrusion in Guaymas Valley, Mexico from time–domain electromagnetic soundings

 

Silvia Martínez–Retama^1,2, Carlos Flores^1,* and José Castillo–Gurrola³

 

¹ Departamento de Geofísica Aplicada, Centro de Investigación Científica y Educación Superior de Ensenada, CICESE, km. 107 Carretera Tijuana–Ensenada, Ensenada, Baja California, México. * Corresponding author: cflores@cicese.mx

² Departamento de Geología, Universidad de Sonora, Blvd. Luis Encinas y Rosales, Hermosillo, Sonora, México. Email: smartine@cicese.mx

³ Departamento de Agricultura y Ganadería, Universidad de Sonora, km. 21 Carretera Bahía de Kino, Hermosillo, Sonora, México. Email: jcg@rtn.uson.mx

 

Received: August, 19, 2006
Accepted: June 19, 2007

 

Resumen

El grave problema de intrusión salina en el Valle de Guaymas, Sonora, se estudia con 44 sondeos electromagnéticos transitorios. La distribución de la resistividad en la parte sur del valle es simple. Una capa conductora asociada con la intrusión salina en el acuífero superior muestra un aumento sistemático de la resistividad tierra adentro. Bajo tres sondeos pudimos diferenciar una base de menor resistividad dentro de este conductor, lo cual sugiere una mayor salinidad en el fondo. La zona norte tiene una estructura eléctrica más complicada, aunque todavía puede reconocerse el conductor de resistividad creciente. Los resultados sugieren que el acuífero inferior no está afectado por la intrusión.

Las conductividades eléctricas están sesgadas respecto a la predicción hecha con la Ley de Archie cuando se grafican contra las salinidades. La presencia de lentes de arcilla en los sedimentos no saturados puede explicar el sesgo y la dispersión de las conductividades.

Palabras clave: Valle de Guaymas, intrusión salina, sondeos electromagnéticos transitorios y de resistividad.

 

Abstract

A severe salt water intrusion in Guaymas Valley, Sonora is mapped by means of 44 time–domain electromagnetic soundings. In the southern part of the valley the resistivity distribution is simple. A conducting layer associated with the saline intrusion in the upper aquifer shows a systematic increase of resistivity inland. Three soundings feature a low– resistivity layer within this conductor, suggesting higher salinity at the bottom. The northern zone has a complex electrical structure, but a conductor with increasing resistivity can be recognized. The results suggest that the lower aquifer is not affected by the intrusion.

When plotted against salinity the conductivity is biased with respect to the predictions of Archie's Law. Clay lenses in the unsaturated sediments may account for the bias and dispersion of conductivities.

Key words: Guaymas Valley, saline intrusion, transient electromagnetic and resistivity soundings.

 

Introduction

Guaymas Valley, near the south coast of Sonora, Mexico (Figure 1a), is an important agricultural district in a semi–arid region (320 mm of annual average precipitation). As in many coastal areas, the groundwater is affected by the intrusion of seawater due to excess water pumping over a fresh water recharge of 30 million cubic meters/year (Castillo et al., 2002). The intensive irrigation of the valley started in the 1950's, and by 1954 more than 100 wells were pumping close to 80 million cubic meters/year of groundwater. The water table dropped below sea level over a wide region. The overdraft increased in the 1960's, with more than 250 wells pumping 200 million cubic meters/year. About 8,000 hectares of agricultural land were lost because of excess water salinity (Macías et al., 1975).

In 1967, federal regulations reduced pumping to about 80 million cubic meters/year in 2004. The water table reached their maximum depths of about 110 m in the late 1990' s, but has recovered about 15 m, due mainly to saline intrusion. Figures 1b and 1c show water table elevations and Total Dissolved Solids (TDS) after a period of about 20 years (Ríos and Ferrer, 2000; Canales et al., 2000). Notice that the water table near Maytorena recovered in 2004, but the TDS increased sharply.

Guaymas Valley is a graben bounded by north–south trending faults, along the Sierra Santa Ursula to the west and the Sierra El Bacatete to the east (Figure 2). Both ranges comprise felsic to intermediate volcanic flows and tuffs of Miocene age (11–23 Ma), unconformably resting on late Cretaceous intrusive rocks (63 Ma). Both are overlain by 8.5 Ma–old basaltic flows (Roldán–Quintana et al., 2004). Dikes and small stocks of rhyolitic composition intrude the Miocene volcanic section along the edges of the graben. The graben formation is associated with the opening of the Gulf of California.

The subsurface geology is shown in Figure 3a, from several drillholes located close to the profile. Coarse and medium grained sediments (boulders, cobbles, gravels and sands) are grouped together while fine–grained clay layers are emphasized because their low resistivity; a black–filled area is used when clay is the sole component of a layer and gray when clay is mixed with other coarser sediments. The geohydrologic model of Macías et al. (1975) is also shown. It consists of two aquifers of clastic sediments separated by an apparently continuous sequence of marine clays, known as the Blue Clay sequence. The upper aquifer has a thickness of up to 160 m and is formed by boulders, gravel, sand, and clay layers in a chaotic sequence. This is highlighted in Figure 3b, which shows the lithologies from seven twin holes. In each pair, the holes are separated by less than 100 m. Note the poor lateral correlation between holes and the limited lateral extension of the clay layers. The lower aquifer contains gravel, sand, clay, and conglomerates to a thickness of up to 200 m resting on granitic and metamorphic rocks, the impervious basement of the region. The Blue Clay contains lenses of gravel and sand and has thicknesses of 130, 170, and 43 m; it thins landwards and disappears between holes PGB6 and PCGB1. To the north both aquifers merge, where gravel, sand, and conglomerate contain some basalt flows.

The basement morphology (Figure 3) is interpreted from a gravity survey by Alvarez (1991) along profile B–B', about 3 km to the East of profile A–A' (Figure 2). Depth to basement was estimated by Alvarez from 2D modeling of the residual anomaly, assuming a density contrast of 670 kg/m³ between the sediments and the basement. There is a mismatch of about 100 m, but the agreement between this gravity–derived basement and the depths to basement at holes PGB14 and PGB6 is reasonable. The basin is thickest about 15 km from the coast, with a significant thinning inland.

The presence of a geothermal component in the groundwater not polluted by the saline intrusion has been suggested by several authors (Verdugo, 1983; Herrera et al., 1984; Alvarez, 1991; Prol–Ledesma, 1991). This proposal is based on high well temperatures, the extensional tectonic regime that has allowed the emplacement of intrusive bodies and the ascent of lava flows, and the proximity of the young oceanic spreading center of the Guaymas Basin in the Gulf of California (Lawver et al., 1975). Figure 4a shows the temperatures measured by Prol–Ledesma (1991) in 10 wells in the valley (locations are indicated in Figure 4b); their anomalously high geothermal gradients vary from 4 °C/100 m to 9 °C/100 m. This author also estimated temperatures with the silica, Na–K–Ca, and K/Mg geothermometers in water samples of 46 wells and one spring. Figure 4b shows the location of these samples and the isotherms estimated with the K/Mg geothermometer, where three zones with higher temperatures (in the 55–60 °C range) can be noted, located in the Sierra Santa Ursula and in the northern and southeastern portions of the valley. Within our study area the estimated temperatures are in the 45–50 °C range. As these temperatures agree with the extrapolation of the temperatures measured in the wells to a depth of 200 m, Prol–Ledesma suggests that the waters reach their equilibrium temperature at this depth. Regarding their chemical composition, the non–polluted waters have a bicarbonate nature with moderate and local concentrations of sulphates, which suggests that their high temperatures are mainly produced by deep circulation with a possible component associated with the igneous intrusions. It is worth to note the absence of hot springs in the valley, which disfavors the presence of important upflow zones.

Electrical resistivity in this area was investigated by Macías et al. (1975), Herreraet al. (1984a; 1984b), Alvarez, (1991), Canales et al. (2000), and Castillo et al. (2002). Most of the resistivity soundings were shallow, carried out with electrode spacings of less than 300 m. The work by Herrera et al. (1984a; 1984b, referred as Herrera et al.) had better coverage and reached greater depths of investigation. They interpreted 141 resistivity sounding using the Schlumberger configuration, with 2 km spacing between soundings and maximum electrode separations (AB/2) of 1 km (Figure 5). Figure 6 shows their resistivity section and geohydrologic model along the southern portion of line N3, a south–north profile of 18 soundings (Figure 5). They proposed an extensively faulted subsurface and an irregular main electrical conductor associated with clays, which differed from the model of Macías et al. (1975) in Figure 3a. Herrera et al. suggested that the sediments underlying the Blue Clay do not form a good aquifer because of high clay content and the presence of salt water. Other authors after 1984 adopted the geohydrologic model proposed by Herrera et al. but there has been some debate on its validity. Canales et al. (2000) mapped the saline intrusion along several profiles and different subsurface elevations using smooth inversions of transient electromagnetic data, but did not incorporate the subsurface lithologies into their models.

Their study area included the Boca Abierta Valley, located east of the Sierra de San Francisquito (Figure 2), as well as the central part of our study area.

We used transient electromagnetic (TEM) soundings (also known as time–domain electromagnetics) to study the saline intrusion in the southern Guaymas Valley. This technique has been widely used (Stewart and Gay, 1986; Fitterman, 1987; Kafri and Goldman, 2005). First, we invert the TEM data along three profiles and we construct geoelectric and geohydrologic models, which differ from those proposed by Herrera et al. Then, we reinterpret the resistivity soundings of Herrera et al. close to our lines and we show that the results are compatible with our TEM–derived models. Finally, the relationship between the electrical conductivity of the upper aquifer and water salinity is analyzed.

Transient electromagnetic soundings

The locations of our 44 transient electromagnetic soundings are shown in Figure 5. They are distributed along three north–south lines normal to the coast, with separations varying from 2 to 6 km. The mean separation between soundings was close to 2 km. The field data were acquired in five campaigns, in 2004 and 2005. Square and rectangular loops were used to generate the source fields. Their dimensions and shapes depended on access, available space and land–owner permits; dimensions of 300 by 300 m to 150 by 150 m were common. We tried to use large loops to reach the maximum depths of investigation with the available equipment. Only 20 % of the soundings were acquired with the 150 by 150 m loops. Voltages were measured with a horizontal coil at the center of the loop, employing a Geonics TEM57 system with frequencies of 30, 7.5 and 3 Hz. A total of 60 stacked voltages were obtained for each sounding. Care was taken to maximize the signal–to–noise ratio. Each voltage curve was the result of 480, 240, and 720 stacks for 30, 7.5, and 3 Hz repetition frequencies, respectively. We carried out five realizations for each frequency, which were averaged to yield the final voltages. If necessary, raw voltages were edited by eliminating outliers. This process was applied to only 0.6 % of all voltages, mainly to the late–time data, where natural electromagnetic noise produced scattered data in some soundings. In seven soundings some late–time voltages were discarded because of large standard errors and scattered data.

Data inversion

The data for each sounding were inverted assuming a layered earth. We used a linearized iterative algorithm based on singular value decomposition of the Jacobian matrix (Jupp and Vozoff, 1975). The rectangular or square loops were approximated to equal–area circular loops; this approximation distorts only the early–time data and is negligible when the shallow structure is moderately resistive (Flores Luna, 2000). The solution of the direct problem needed in each iteration was obtained with digital linear filters as in Anderson (1975; 1979). The effect of the linear turn–off ramp was accounted for by convolving the current ramp with the step turn–off response (Fitterman and Anderson, 1987).

The final inverted model was selected as having the minimum root mean squared (rms) misfit error and the minimum number of layers. The definition of the rms error used in this work was

where N is the number of data points (usually 60), d_i are the observed voltages, c_i the calculated voltages, and σ_i. the standard errors of the observed data. A misfit error of unity indicates that the model reproduces the observed data as well as the data errors permits.

The optimal model was found by a random search around a preliminary model, also known as Monte Carlo search (e.g., Jones, 1982). In this approach all model parameters, i.e., layer resistivities and thicknesses, were randomly perturbed by up to +/– 25 % around the preliminary model to define the initial model in new data inversions. An inverted model replaced the previous one if it produced a significant decrease in the misfit error. The process was repeated about 20 times. This procedure was also used to estimate the uncertainties of the model parameters. To this end we considered the upper and lower variation bounds for all models with misfit errors falling within 2 % of the error of the best model. This approach of error estimation was complemented by perturbing only the two parameters of a layer suspect of having an equivalence problem, or by perturbing single parameters such as the resistivity of the last layer, or of a high resistivity layer.

Results

The final models had between two to five layers. Most of them (60 %) contained four layers. The voltages were adequately matched by the calculated responses of the inverted models. The average misfit error was 1.58, with a standard deviation of 0.43. The whole set of inverted models is described in Martínez Retama (2007). Figure 7a displays the results for six soundings to illustrate the main features of the dataset. The upper panels of each sounding include the observed apparent resistivities and their corresponding standard errors, solid lines for the calculated responses, and the rms misfit error (ε). These responses are late–time apparent resistivities, derived from the late–time asymptotic approximation by Kaufman and Keller (1983), following the usual convention (Spies and Frischknecht, 1991). Notice that even for the homogeneous half–space, late–time apparent resistivities tend to increase in early–times, unlike what happens with short electrode separations in resistivity soundings. The lower panels in Figure 7a show the final inverted models with the estimated uncertainties in the resistivities and interface depths displayed as error bars. Arrows in the upper bars indicate that the upper bound falls outside the plotted area. The most relevant feature is the presence of a conductive layer at depth. Only one of the 44 soundings was not inverted to a layered medium (sounding 41), because the data suggest dispersive effects. Figure 7b shows the observed voltages for this sounding, located a few tens of meters from a basalt outcrop of the Sierra San Francisquito. The late–time data are negative, suggesting induced polarization effects.

Figure 8 illustrates the approach used to estimate model uncertainties for sounding 10. Fifteen different models (Figure 8a) reproduce the observed data with a misfit error less than 1.639 (Figure 8b), 2 % above the error of 1.607 for the best model (Figure 8c). The fit between calculated and observed apparent resistivities is good except at the three early–time data. Figure 8c shows the estimated error bars for four layer resistivities and three interface depths. The third layer corresponds to the seawater–contaminated aquifer. This layer is well resolved and does not suffer from any serious equivalence problems. This result is also valid for the rest of the soundings. Figure 8a shows that the resistivity of the second layer varies between 70 Ωm and values higher than 10,000 Ωm. This is an expected result; electromagnetic methods have this problem because little current is induced in high–resistivity layers. However, the thickness of this layer has low error and the depth to its top is reasonable well resolved. In about 33 % of the models, there is little sensitivity to high–resistivity layers (Figure 8c).

Resistivity sections were constructed by stitching the layered models together. Figures 9, 10, and 11 emphasize different aspects of these results. Figure 9 shows the three sections with the depths to the layer interfaces, with uncertainties plotted as error bars. For clarity, the shallowest layers are not displayed. The proposed correlations between interfaces of neighboring models are depicted with dashed lines. This figure includes the lithology of nearby drillholes where the clay horizons are emphasized with a solid pattern. Drillholes located more than 1 km away from the sections are indicated by dashed lines. The depths where the drillholes penetrated the top and bottom of the Blue Clay are indicated, showing also the interpolation of its top with small crosses. The depths to the water table for the year 2004 are plotted with small circles, and the values of Total Dissolved Solids (TDS) (Canales et al., 2000), projected along the three lines for the year 2000, are shown in the upper panel. Unfortunately, no TDS data for 2004 are available. Figure 10 displays the layer resistivities with a logarithmic color code, using five equally–spaced intervals per decade, with our interpretation in terms of a geohydrologic model. Finally, Figure 11 portrays, for the vadose zone, upper aquifer, Blue Clay, and lower aquifer, the spatial variation of the resistivity along the three lines with the corresponding uncertainties displayed as error bars.

The spatial behavior of the resistivity in the three sections can be divided into southern and northern zones; the division occurs about 14 to 16 km from the coastline. In the southern zone the behavior is simple and clear, unlike some locations of the northern zone.

The southern zone

This zone is characterized by good lateral correlation between different interfaces. Clearly shown in Figures 9 and 10 is the presence of a conductor with resistivities varying from less than 1 Ωm at the coast to values close to 4 Ωm at 16 km from the coast (Figure 11). This conductor practically outcrops at the coast, gradually deepening inland. Its top is close to the water table, while its bottom closely follows the depth to the top of the Blue Clay unit. All these features, clearly indicate that the conductor is the electrical expression of the upper aquifer intruded by sea water. The TDS profiles displayed in the upper panel of Figure 9 show a systematic decrease of the water salinity away from the coast, except for a local high in Line 3, likely due to excessive pumping of the aquifer by the nearby water wells. A quantitative correlation between the TDS values and the conductivity of the upper aquifer is discussed below. The resistivities of the deepest medium must be associated to the Blue Clay unit, which although higher than those of the upper aquifer, have relatively small values, varying from 2.5 to 22 Ωm. Soundings 5, 27, and 15 in Figure 7a, and 10 in Figure 8, are examples of the data and models in the southern zone, where it can be noticed that the main conductor is well resolved because the uncertainties in its resistivity and in the depths to its top and bottom are quite small. As mentioned above, the least resolved parameter is the resistivity of a resistive layer associated with the vadose zone under some soundings, as is the case for soundings 10 and 15. Except at sites 14 of Line 2, and 46 of Line 3, no deeper interface could be detected below the top of the Blue Clay. The resistivities of the upper aquifer and Blue Clay are so low that practically all the subsurface current is induced in them, impeding the detection of deeper interfaces. In order to significantly increase the depth of investigation, other geophysical technique, such as magnetotellurics, should be applied.

An interesting feature occurs in Line 2 from 13 to 18 km from the coast (Figure 9). Under three contiguous sites (15, 17, and 18) the upper aquifer conductor can be differentiated into two layers. The upper layer/lower layer resistivities in these soundings were 4.1/2.5, 7.1/4.7, and 7.7/5.0, with the lower layer being more conductive. Although these are not strong resistivity contrasts, the layering can be justified by the fact that the resistivity error bars do not overlap in any case. We interpret this intra–layering within the main conductor as a gradational increase with depth of the salinity within the saturated upper aquifer due to the higher density of saltier water.

The northern zone

In this zone the resistivity of the upper aquifer still shows a systematic increase inland (Figure 11), likely due to a decrease of water salinity. However, the electrical structure in this zone is more complicated (Figures 9 and 10), evidenced by the following problems: a) in many locations the depth to the 2004 water table does not agree with the depth to the top of the conductor, b) there are regions where the lateral continuity between layer interfaces is hard to define, and c) the association between the base of the conductor and the Blue Clay is not longer clear. We propose that the presence of many clay layers in the clastic sediments overlaying the Blue Clay is producing the problems in a) and b). From the lithologic evidence found in the seven twin holes (Figure 3b), these clay layers are characterized by variable thicknesses, they occur at different depths, and have typical horizontal dimensions of less than 100 m because the twin drillholes are less than 100 m apart. This disorderly array of clay lenses represents a source of noise to the horizontally homogeneous layer assumed in the inverted models. Although these clay lenses also exist in the southern zone, there the upper aquifer has such low resistivities that its signal is much stronger than the noise from the disordered clay layers. In contrast, in the northern zone the resistivities of the upper aquifer have higher values (Figure 11), such that the global effect of these clay layers may give a shallower depth to the top of the conductor. Regarding problem c), the relatively strong resistivity contrast between the upper aquifer and the Blue Clay that exists in the southern zone is no longer present in the northern zone. Here, the aquifer has resistivities similar to those of the Blue Clay, and even there are some soundings where the resistivity of the Blue Clay is lower than that of the upper aquifer. The weighted average of the resistivity of the Blue Clay for the three lines is 6.04 +/– 1.31.

The higher resistivities found in the northern zone allowed deeper penetrations of the induced current, permitting the detection of interfaces below the Blue Clay, such that there are twelve estimates of the resistivity of the lower aquifer (bottom panel of Figure 11). The weighted average of these resistivities, that is, considering the individual errors in the calculation of the average, is 8.4 +/–2.9. This value is similar to the weighted average resistivity of the upper aquifer in the most northern soundings (7.0 +/– 3.4), where the groundwater is not affected by the saline intrusion. Then, we find no supporting evidence for a saline and low–permeability lower aquifer, as proposed by Herrera et al. (1984) because its resistivity is comparable to the upper aquifer with fresh water and the few drillholes that reach the lower aquifer do not intersect any clay layers.

A resistivity of 35 Ωm, found under soundings 39 of Line 2 represents the only estimate of the basement resistivity. Although this value is not particularly high for an impervious basement, the clay content of the slate found in drillhole PGB–6 (Figure 9) can explain its relatively low value.

The geohydrologic model of Herrera et al. along Line N3, shown in Figure 6b, is significantly different from our model under Line 2 (Figure 10). These two lines (N3 and 2), although do not share their starting and ending points, are almost coincident for a length of 23 km (Figure 5). The model by Herrera et al. (Figure 6) implies intensive faulting, not only of the basement but of practically all the sedimentary cover, and they associate the main conductor to different geologic units having variable clay contents. Our model (Figure 10) does not favor a dislocated faulted subsurface. This is supported by the continuity of the Blue Clay, which works as an index horizon. Besides, we interpret the main conductor as the upper aquifer, associating its variable resistivity with water salinity. Notice that the VES data of Herrera et al. were acquired in 1984 and our TEM data in the years 2004–2005. After 20 years of aquifer exploitation one would expect some changes in the subsurface resistivities, more likely in the thickness and resistivity of the upper aquifer. However, as the geology has not changed in this time, we believe the two models should not be so different.

Inversion of resistivity data

Unconstrained inversions

In order to find the source for the discrepancy between the model of Herrera et al. and our TEM–derived model, we interpreted their resistivity soundings starting from the raw data, considering not only the soundings of Line N3, but all soundings close to our three lines. A total of 40 Schlumberger soundings were analyzed (Figure 5), all of them having 19 apparent resistivity values for half–electrode spacings (AB/2) ranging from 1 to 1000 m. As the original voltage/current ratios were not available and the apparent resistivity values were read from plotted soundings, we assigned a 5 % uniform standard error to the apparent resistivity values. This percentage error is equal to the minimum error assigned to the TEM voltages. The location of the resistivity soundings in our map is approximate as their UTM coordinates are not available. However, we estimate an error in location of the order of 200 m.

As interpretation strategy, we inverted the VES data trying to minimize the inherent bias of the interpreter. Consequently, as a first step in the interpretation each sounding was inverted using the Occam or smooth approach (Constable et al., 1987), which constrains the data inversion process by minimizing the vertical variation of the resistivity of a large number of thin layers while simultaneously minimizing the misfit between observed and calculated responses. Although this method is relatively immune to the bias of the interpreter, there are a number of parameters which influence the final model, such as the number of layers, the minimum and maximum interface depths, and the smoothness of the final model. We used the same number of layers as the number of apparent resistivity data, and minimum and maximum interface depths of 0.5 and 500 m, following the rule of thumb that the maximum depth of investigation with the Schlumberger array is half the current electrode separation AB/2. In each iteration of Constable's algorithm the misfit error is decreased at the expense of the roughness of the model. For the preferred solution we looked for a compromise between the quality of fitness and the model roughness. When plotting the rms error against roughness, this compromise usually occurs at the vertex of a curve with shape of an "L".

As the second step in the interpretation process the soundings were inverted to the familiar stratified models with a small number of layers. For this purpose, the generalized linear inversion algorithm of Jupp and Vozoff (1975) was used. The initial model required in each inversion was defined from the behavior of the corresponding Occam model, i.e., the depths to the layer interfaces were defined where the resistivities of the smooth model showed the highest vertical gradient. An example of this procedure is shown in Figure 12 for sounding E5–4, which displays the smooth model, the initial model defined for the layered inversion (Figure 12a) and the final layered model (Figure 12b). Most of the inverted resistivity models (93 %) were of 4, 5 or 6 layers. The average misfit error for this set of 40 models is 1.649, with a standard deviation of 0.720. These latter values are similar to those obtained for the TEM inversions. The layered models determined with this process are denoted here as unconstrained models because no a priori information was used in their estimation.

Figure 13a shows the smooth or Occam section constructed by stitching together and contouring the 1D Occam models, Figure 13b the 1982 TDS profile, and Figure 13c the section formed by the unconstrained layered models, where the uncertainties in the layer interface depths are indicated with error bars. In this figure the structure shallower than 20 m is omitted. Although there are differences between the resistivity section interpreted by us (Figure 13c) and that from Herrera et al. (Figure 6a), the important feature to notice is that in both sections the resistivities have a high lateral variability and the proposed correlations between interfaces are abrupt. Furthermore, the depth to the top of the conductor does not systematically agree with the depth to the water table, and the depths to the bottom of the main conductor have significantly large uncertainties. This latter feature is produced by equivalence problems, as will be discussed later.

Constrained inversions

With the aim of exploring if a resistivity section similar to the TEM–derived section can be obtained from the VES data, we assumed that the depth and thickness of the conductor associated with the upper aquifer are similar in both data sets, i.e., that they have not changed significantly in the 20–year span between 1984 and 2004. The conductor derived from the TEM soundings has the important advantages that both boundaries are relatively well resolved and that they generally have smooth lateral variations. This assumption has two components: the base and the top of the conductor. Regarding the base, the resistivity contrast between the lower part of the aquifer and the Blue Clay should have already existed in 1984, so we consider this is a robust assumption. The depth to the top of the conductor merits a more detailed analysis. The depth to the water table certainly has changed from 1984 to 2004, as there is a difference in depth of up to 18 m where the water table is depressed most (the Maytorena depression). However, this difference seems not to be important for both geophysical methods, because neither the TEM soundings (except in the southern zone, Figures 9 and 10), or Herrera's interpretation (Figure 6a), or our unconstrained interpretation (Figure 13c) gave systematic agreements between the water table and the top of the conductor. Then, we deduce that this discrepancy is not due to a limitation of the particular geophysical method, but must be produced by the subsurface resistivity distribution, the already mentioned effect of the conductive clay lenses in the sediments overlying the Blue Clay.

The procedure to incorporate the TEM main conductor into the VES models was by inverting again the 40 resistivity soundings using as initial models the unconstrained final models modified by including the depths to the top and bottom of the TEM conductor and using the principle of equivalence to modify the conductor's resistivity. If necessary, additional layers were added to improve the fit. In this process all layer parameters were freed to vary in the inversion. Because we are including a priori information not pertaining to the VES soundings, we will denote these models as constrained models. The average misfit error and standard deviation for the 40 soundings were 1.650 +/– 0.640, values very similar to those obtained for the unconstrained models (1.649 +/– 0.720). These results show that the constrained models are as valid as the unconstrained ones because they reproduce the observed data almost equally well.

Employing the same format of the TEM results, the sections of constrained inversions for the three lines are shown in Figures 14, 15, and 16. Figure 14 displays the depths to interfaces, together with the proposed lateral correlations between soundings. We include also the depth to the 1984 water table, the top and bottom of the Blue Clay as found in the drillholes, and profiles of the 1982 Total Dissolved Solids (TDS). Unfortunately, no TDS data are available for the year 1984. Structure shallower than 20 m is again omitted in this figure. Notice the reduced uncertainties of the base of the main conductor compared to those of Figure 13c. Figure 15 shows the colored sections with the same color scale of Figure 10 and the interpreted geohydrologic model. Figure 16 displays the lateral variation of the resistivities in the vadose zone, upper aquifer, Blue Clay, and lower aquifer. The vadose zone in the inverted models generally is composed by more than three layers. Instead of presenting the resistivities of each one of these layers, the resistivity of the so called vadose zone in Figure 16 is that of the layer immediately over the conductor, which generally is the thickest and more resistive.

The resistivities of the vadose zone (Figure 16) display a significant data dispersion, which is again interpreted as the effect of the chaotic distribution of the clay lenses. The resistivities of the upper aquifer (Figure 16) also show a general increase as the distance from the coast increases, likely associated with the inland decrease of aquifer salinity. The upper aquifer resistivities, compared to the values estimated from the TEM soundings (Figure 11), are more disperse and generally have higher values, qualitatively agreeing with the lower salinities in the year 1984. In several soundings located in the northern part of the sections the resistivity of the Blue Clay is lower than the resistivity of the saturated upper aquifer, a feature also found in some TEM models. Estimates of the resistivity of the lower aquifer were obtained only under three soundings, compared with twelve cases with the TEM method, showing that the currents induced with TEM soundings with 300x300 m loops penetrated deeper than the currents impressed by Schlumberger soundings with maximum electrode separations (AB/2) of 1 km. This statement is supported with the histogram of depths to the deepest layer interface of Figure 17, which shows that, for depths greater than 300 m, there are seven TEM models compared to only three VES models.

One reason for the poor lateral correlation of the unconstrained resistivity section of Figure 13c is the presence of equivalence problems in several layers of the models. The principle of equivalence (Orellana, 1972) in the conductance and resistance of a layer occurs in thin layers with high conductivity and resistivity, respectively. In the first case the layer conductance (the ratio of thickness/resistivity) is well resolved by the data, but not the thickness and resistivity separately. Therefore, there are a large number of possible thickness/resistivity combinations that fit the observed data to practically the same degree. The problem of equivalence in the resistance (the product of thickness times resistivity) is similar, such that the resistance may be well resolved but not the resistivity and thickness individually. Figure 18 illustrates such equivalence problems for sounding E5–4, which is located less than 1 km from the TEM sounding 10 portrayed in Figure 8. Figure 18a shows nine possible five–layer models that fit the observed data with a misfit error less than 0.95. This value is 2 % higher than the 0.93 error of the best constrained model (Figure 18b). The first and second layers are well resolved while the third layer has an equivalence problem in its resistance, but is not too severe. In contrast, the fourth layer, associated with the upper aquifer, suffers from a strong equivalence problem in its conductance.

 

Correlation between electrical conductivity and salinity

The values of 51 out of the 87 upper aquifer conductivity estimates are plotted in Figure 19a as a function of their salinity using logarithmic scales. The salinities for each sounding were estimated by interpolation from the TDS maps of Figure 1c, using the 1982 map for the 1984 resistivity soundings and the 2000 map for the 2004–2005 TEM soundings. For the remaining 36 conductivities there are no TDS data in the vicinity of the corresponding soundings. The salinity dataset has the apparently serious limitation of not being contemporaneous with the geophysical surveys. The uncertainties in the conductivities are denoted with error bars in Figure 19a. The corresponding uncertainties for the salinities are difficult to evaluate because the degree of vertical mixture between fresh and sea water at a given well is not known. As mentioned above, under three soundings we found a more conductive layer at the base of the upper aquifer, a likely evidence of a vertical gradient of salinity. Although the data of Figure 19a show a general increase of conductivity with salinity, the points have a considerable dispersion. This figure shows a best–fit straight line obtained by fitting the data with the weighted least squares method. The envelope around the straight line indicates that within the enclosed area falls the true line with a 90 % confidence level. An rms misfit error of 48.9 reflects the high data dispersion. In order to have an idea of the source of such dispersion, we carried out the following analysis.

The empirical relationship between the bulk conductivity σ_r of a rock composed of granular sediments saturated with water of conductivity σ_w is,

known as Archie's Law, where F, the formation factor, depends on the porosity and fabric of the rock. On the other hand, laboratory measurements have shown that the water conductivity and the amount of dissolved salts are linearly related when plotted in logarithmic scales, that is,

where m₁ and b₁ are the slope and intercept of the straight line, and TDS are the Total Dissolved Solids expressed in parts per million. The values of m₁ and b₁ depend on the type of salt in solution and temperature. Considering that the salt is sodium chloride at 35 °C, which is the average temperature in the middle part of the upper aquifer (Figure 4a), the values of m₁ and b₁ are 0.951 and –3.50, respectively (Davies and DeWiest, 1966; Keller and Frischknecht, 1966). Applying the logarithm to Archie's Law and substituting the last expression, we obtain

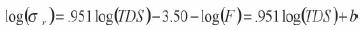
which again is a straight line of slope .951 and intercept b = –3.50 – log (F) if both the rock conductivity and TDS are plotted with logarithmic scales.

To estimate the formation factor, we considered the upper aquifer resistivities estimated at the three TEM soundings located right at the coast (soundings 4, 5, and 40, with resistivities of .948, .988, and .929, average of .955 Ωm), assumed the aquifer is 100 % saturated with sea water of resistivity 0.2 Ωm, and applied Archie's Law, obtaining a value for F of 4.78, giving the relationship,

plotted in Figure 19a with the label "expected".

There is a clear discrepancy between the experimental best fit line and the expected line, the main difference coming from the different intercepts, such that almost all data points have conductivities higher than the expected line. To find the source of the discrepancy, let us recall the assumptions on which we determined the expected line: a) the only solid in solution is sodium chloride at an homogeneous 35 °C temperature, b) there is a 100 % water saturation in the pores of the rock, c) Archie's Law controls the relationship between the bulk conductivity and the water conductivity, and d) the formation factor is homogeneous over the whole area. It is unlikely that the presence of other salts in solution or other temperatures could reduce significantly the discrepancy. If hot fluids of geothermal origin locally exist in the upper aquifer, they are already considered in the conductivity and TDS data. Considering saturations less than 100 % increases the discrepancy because the intercept of the expected line decreases. The assumption of a homogeneous formation factor may not be strictly valid, but to reduce the discrepancy would require a formation factor more than one order of magnitude smaller than the estimated value of 4.78. The most likely source for the discrepancy is that Archie's Law has a limited application in this inhomogeneous environment. The systematic bias of the experimental data toward the more conductive side of the expected line suggests that the conductive clay lenses present in the sediments overlying the Blue Clay, and mainly those immersed in the resistive unsaturated zone, are perturbing and biasing the conductivity of the upper aquifer estimated with the geophysical methods. To modify Archie's Law by including an additional term representing these clays may not be valid because their effect on the conductivity of the upper aquifer depends on the depths, thicknesses, and conductivities of the clay lenses, and on unknown geometrical relationships between the transmitter, the receiver, and the clay lenses.

Estimation of porosity

From the formation factor estimated above we can determine a range of values for the porosity (Φ) with Archie's Law, F=aΦ^–m, where a and m are empirical parameters dependent on the rock fabric. For late Tertiary sediments of the Guaymas Valley a and m may vary from 0.7 to 0.8, and 1.4 to 1.7, respectively (Orellana, 1972), giving porosity values ranging from 23 % to 37 %, with a mean value of 30 %. An argument in favor of using Archie's Law for this derivation is that under the three TEM soundings located right at the coast the resistive vadose zone is practically absent, such that the perturbing effect of the clay lenses might be small.

Saline interface

The saline intrusion into coastal aquifers is a gradational mixture process, varying between the sea water and fresh water end members. Therefore, the determination of the saline interface requires a previous definition of a salinity threshold, such as the conventional 1000 ppm freshwater value. Because of the rather poor correlation between conductivity with salinity, we can not define a saline interface in these terms. However, the similar shapes of the lateral variation of the TEM upper aquifer resistivity along the three lines (Figure 11) is an important result, sufficiently robust as to be ignored. The corresponding shapes of the VES upper aquifer resistivity are not similar and show a significantly higher dispersion (Figure 16). This can be explained by the fact that small–scale near–surface changes in resistivity are much more likely to affect grounded–wire techniques (such as VES) than purely inductive loop–loop methods (Spies and Frischknecht, 1991). Such similitude is highlighted in Figure 19b, where the resistivities of the three lines are superimposed. In order to estimate the location of the maximum horizontal gradient, the data was fitted to a fourth degree polynomial with the weighted least–squares method. The maximum slope of this polynomial occurs at a distance of 9.1 km from the coast, which can be interpreted as the location of the maximum lateral gradient in concentration, which we will denote as the saline intrusion interface.

Conclusions

From the layered inversions of 43 TEM soundings the behavior of the subsurface resistivity can be characterized into southern and northern zones, the division occurring at about 15 km from the coast. In the southern zone there is a good lateral correlation between layers, standing out a well resolved conductor which shows an increasing resistivity away from the coast. Clearly, this conductor is the upper aquifer intruded by saline marine water as its top agrees with the water table and its bottom with the impervious layer represented by the Blue Clay. The low resistivities characteristic of this zone did not allow the induced currents to penetrate deeper than the Blue Clay. In the transition zone between the southern and northern zones we found evidence of internal layering within the main conductor at three contiguous soundings, likely associated with denser saline water within the upper aquifer.

In the northern zone the main conductor with an increasing resistivity inland is also evident, but the agreement of its top and bottom with the water table and the Blue Clay, respectively, are no longer clear under many soundings. These problems are likely due to the combined effect of the noise produced by the series of clay lenses present in the granular sediments overlying the Blue Clay and the absence of strong resistivity contrasts in the subsurface materials. An advantage of the higher resistivities of the northern zone is that the induced currents penetrated below the Blue Clay, giving twelve estimates of the resistivity of the lower aquifer. The weighted average of these resistivities is similar to the average resistivity of the upper aquifer in the non–saline zone. This result can be considered as evidence of a lower aquifer not affected by the saline intrusion, at least in the central and northern zones of the survey area. There was only one estimate (35 Ωm) of the basement resistivity, confirmed by a nearby drillhole where slate was intersected near its bottom.

Seven pairs of closely–spaced drillholes indicate that typical lateral dimensions of the clay lenses are less than 100 m. These confined, and conductive bodies embedded in the resistive unsaturated granular sediments represents a three–dimensional (3D) problem for these geophysical techniques. To carry out a 3D interpretation of the data would require, at least, having a 2D array of soundings with minimum separations of the order of 50 m.

The geophysical and geohydrological models of Herrera et al. along their line N3 do not agree with our model along our line 2. We inverted their resistivity data and obtained unconstrained models with a thick and irregular conductor, similar to that found by them, where many models suffer from a non–uniqueness (equivalence) problem. We proved that by including the conductor's thickness estimated with the TEM inversions into the initial guess VES models, we obtain constrained models which fit the data as well as the unconstrained models and the resistivity sections are similar to the TEM sections. With this approach, applied to 40 VES located close to our three lines, the non–uniqueness of the resistivity soundings is reduced because the TEM models are not affected by equivalence. Consequently, our geoelectric and geohydrologic model agrees with that proposed by Macías et al. (1975), where two aquifers are separated by the Blue Clay. We consider that the Herrera et al's model is not adequate mainly because of the equivalence problem affecting their data.

With the proposed perturbing effect of the clay lenses on the estimated resistivities and layer interfaces, we cannot discard the presence of minor vertical displacements due to faulting in the Blue Clay, probably of few meters in the southern zone and a few tens of meters at most in the northern zone. The presence of faulted blocks with significant vertical displacements, evident in the gravity maps of Herrera et al. (1 984a) and Alvarez (1991), probably affects the basement and the sediments of the lower aquifer, i.e. the major tectonic movements likely occurred previous to the deposition of the Blue Clay.

The TEM method with 300 x 300 m loops penetrated deeper than the Schlumberger array with maximum current electrode separations (AB/2) of 1 km. This statement is inferred from the greater number (12 for TEM, 3 for VES) of lower aquifer resistivity obtained with the TEM soundings.

Both the VES and TEM upper aquifer conductivities are strongly dispersed when plotted against the available aquifer salinities. The least–squares linear fit disagrees with the predicted variation based on Archie's Law. The TDS data do not correspond to the same year of the geophysical surveys, such that part of the discrepancy could be explained by this shortcoming. However, the systematic bias of the actual conductivities respect to the expected line suggests that the heterogeneous electrical nature of the sediments limits the application of Archie's Law to this environment. The multiple clay lenses present in the unsaturated resistive sediments are the most likely candidates for both the bias and dispersion of the actual conductivities.

From the highest lateral gradient of the TEM–derived upper aquifer resistivities we inferred the location of the saline intrusion interface, defined as the highest concentration gradient of the upper aquifer water. This interface is located at 9.1 km from the coast.

By assuming that the perturbing effect of the clay lenses is negligible at the three TEM stations located right at the coast and by adopting Archie's Law, we estimated an upper aquifer fractional porosity range of 023<0.30<0.37.

 

Acknowledgements

We are grateful for the valuable field assistance of J. Calderón and A. Díaz from Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) and the Universidad de Sonora students F. Romero, M.A. Zamudio, C. Buitrón, A. Grijalva, and C. León. The discussions with M. Morales are greatly appreciated. We thank Ing. L. A. Oroz of the Comisión Nacional del Agua for providing the well data. This work was funded by Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) and the Departamento de Geología, Universidad de Sonora internal projects. S.M.R. was supported by a schollarships by Universidad de Sonora and PROMEP. The comments by two anonymous reviewers helped to improve the original manuscript.

 

Bibliography

ANDERSON, W. L., 1975. Improved digital filters for evaluating Fourier and Hankel transform integrals. U.S. Geol. Surv. rep. GD–75–012.        [ Links ]

ANDERSON, W. L., 1979. Numerical integration of related Hankel transforms of order 0 and 1 by adaptive digital filtering. Geophysics, 44, 1287–1305.        [ Links ]

ALVAREZ, R., 1991. Geophysical determination of buried geological structures and their influence on aquifer characteristics. Geoexploration, 27, 1–24.        [ Links ]

CASTILLO, J., M. MORALES, E. VEGA, M. RÍOS, G. MUÑOZ, R. SANDOVAL, J. RODRÍGUEZ, S. MARTÍNEZ, R. IBARRA and G. BORGO, 2002. Disponibilidad y planeación del recurso agua en el municipio de Empalme, Sonora, Report of the Universidad de Sonora to SIMAC–CONACYT, 102 p.        [ Links ]

CANALES, A., R. GONZÁLEZ, J. GARATUZA, D. ENCINAS, S. DÍAZ, N. ESQUER, M. RUELAS, A. FLORES, F. OSORIO, M. GUTIÉRREZ, G. ARMENTA, A. SERNA, J. GARCÍA and F. PABLOS, 2000. Estudio de disponibilidad y actualización hidrogeológica en los acuíferos de los valles de: El Yaqui, El Mayo, Boca Abierta y Guaymas, Sonora, Report of the Instituto Tecnológico de Sonora to the Comisión Nacional del Agua, 167 p.        [ Links ]

CONSTABLE, S. C., R. L. PARKER and C. G. CONSTABLE, 1987. Occam's inversion: a practical algorithm for generating models from electromagnetic sounding data, Geophysics, 52, 289–300.        [ Links ]

DAVIES, S. N. and R. J. M. DE WIEST, 1966. Hydrogeology, John Wiley and Sons, 463 p.        [ Links ]

FITTERMAN, D. V., 1987. Examples of transient sounding for groundwater exploration in sedimentary aquifers. Groundwater, 25, 685–692.        [ Links ]

FITTERMAN, D. V. and W. L. ANDERSON, 1987. Effect of transmitter turn–off time on transient soundings. Geoexploration, 24, 131–146.        [ Links ]

FLORES LUNA, C., 2000. La exactitud del problema directo de sondeos electromagnéticos transitorios, GEOS, 20, 70–88.        [ Links ]

HERRERA, I., R. RODRÍGUEZ, E. LIMA, T. GONZÁLEZ, R. ALVAREZ, L. DEL RÍO, H. NIEDZIELSKY and A. ORTEGA, 1984. Ampliación al estudio geofísico del Valle de Guaymas, Sonora, Report of Instituto de Geofísica, UNAM to the Secretaría de Agricultura y Recursos Hidráulicos, 313 p.        [ Links ]

HERRERA, I., R. RODRÍGUEZ, G. CAMPOS, A. ORTEGA and R. MEDINA, 1984. Anexo de la ampliación al estudio geofísico del Valle de Guaymas, Sonora, Report of Instituto de Geofísica, UNAM to the Secretaría de Agricultura y Recursos Hidráulicos, 102 p.        [ Links ]

JONES, A. G., 1982. On the electrical crust–mantle structure in Fennoscandia: no Moho, and the asthenosphere revealed? Geophys. J. R. astr. Soc., 68, 371–388.        [ Links ]

JUPP, D. L. B. and K. VOZOFF, 1975. Stable iterative methods for the inversion of geophysical data. Geophys. J. R. astr. Soc., 42, 957–976        [ Links ]

KAFRI, U. and M. GOLDMAN, 2005. The use of the time domain electromagnetic method to delineate saline groundwater in granular and carbonate aquifers and to evaluate their porosity. J. Applied Geophys., 57, 167–178.        [ Links ]

KELLER, G. V. and F. C. FRISCHKNECHT, 1966. Electrical methods in geophysical prospecting, Pergamon Press, 519 p.        [ Links ]

KAUFMAN, A. A. and G. V. KELLER, 1983. Frequency and transient soundings, Elsevier Science Pub.        [ Links ]

LAWVER, L. A., D. L. WILLIAMS and R. P. VON HERZEN, 1975. A major geothermal anomaly in the Gulf of California. Nature, 257, 23–28.        [ Links ]

MACÍAS, L., A. RAMÍREZ and A. GONZÁLEZ, 1975. Interpretación de datos y determinación del potencial actual del acuífero en la costa de Guaymas, Sonora, Report from Técnicas Modernas de Ingeniería to the Secretaría de Recursos Hidráulicos, 591 p.        [ Links ]

MARTÍNEZ RETAMA, S., 2007. Modelo geoeléctrico del acuífero del Valle de Guaymas y su intrusión salina usando sondeos electromagnéticos transitorios, Ph.D. Thesis, Earth Sciences Division, CICESE, 160 p.        [ Links ]

ORELLANA, E., 1972. Prospección geoeléctrica en corriente continua, Paraninfo, Madrid, 523 p.        [ Links ]

PROL–LEDESMA, R. M., 1991. Chemical geothermometers applied to the study of thermalized aquifers in Guaymas, Sonora, Mexico: a case study. J. Volcanol. Geotherm. Res., 46, 49–59.        [ Links ]

RÍOS, J. and R. J. FERRER, 2000. Estudio Hidrogeoquímico del Valle de Guaymas, Sonora, B.Sc. Thesis, Dept. of Geology, Universidad de Sonora, 111 p.        [ Links ]

ROLDÁN–QUINTANA, J., G. MORA–KLEPEIS, T. CALMUS, M. VALENCIA–MORENO and R. LOZANO–SANTACRUZ, 2004. El graben de Empalme, Sonora, México: magmatismo y tectónica extensional asociados a la ruptura inicial del Golfo de California. Revista Mexicana de Ciencias Geológicas, 21, 320–334.        [ Links ]

SPIES, B. R. and F. C. FRISCHKNECHT, 1991. Electromagnetic sounding, in Nabighian, M.N., (editor), Electromagnetic Methods in Applied Geophysics, 2, Applications, Part A, 285–386, Soc. Explor. Geophys.        [ Links ]

STEWART, M., and M. C. GAY, 1986. Evaluation of transient electromagnetic soundings for deep detection of conductive fluids. Groundwater, 24, 351–356.        [ Links ]

VERDUGO, F., 1983. Geotermia en Sonora, B.Sc. Thesis, Dept. of Geology, Universidad de Sonora, 119 p.        [ Links ]