Introducción
Los bovinos Siboney con la composición racial de 62.5% de Holstein y 37.5% de Cebú se desarrollaron para las condiciones de pastoreo en las regiones tropicales (López y Ribas 1993, Fernández y Tronco 2011). En la fase productiva, la lactancia se desarrolla a 240 días, se ajusta al modelo de Wood con una curva que incrementa continuamente, con producción máxima de 7.71 kg a los 40 días en lactancia y 1 653 kg promedio de producción total acumulada (Palacios-Espinosa et al. 2016). La edad al primer parto, y la edad y peso al primer empadre ocurre en promedio a los 35 y 24 meses con peso de 306 kg, respectivamente (Portales et al. 2007, Portales et al. 2012). Con relación a las variables de crecimiento, el control de producción contempla el peso vivo en el intervalo del peso al nacer hasta los 950 días de edad (Alonso et al. 2014). Los datos de peso vivo a diferentes edades generan una distribución de puntos a través del tiempo, los cuales permiten describir y analizar el crecimiento animal con base en modelos no lineales (MNL); asimismo, los MNL describen la curva de crecimiento a partir de parámetros con interpretación biológica, como la tasa de crecimiento, el peso adulto o asintótico, grado de madurez, edad y peso al punto de inflexión, entre otros (Domínguez-Viveros et al. 2013, Domínguez-Viveros et al. 2014).
Las condiciones y los parámetros que definen la curva de crecimiento de las vaquillas tienen repercusiones en la vida productiva y reproductiva de la vaca adulta (Galvão et al. 2009, Roche et al. 2015). Se ha planteado que las vaquillas deben llegar a la primera cubrición con un peso mínimo de 50 a 55% del peso vivo adulto (Funston y Deutscher 2004, Roberts et al. 2009). El crecimiento de las vaquillas se divide en dos etapas: la prepuberal que se caracteriza por un crecimiento lineal e isométrico, tras la pubertad el crecimiento pasa a ser alométrico, modificándose principalmente la composición corporal y la relación entre los distintos tejidos; y la pubertad o inicio de la etapa reproductiva influyen (Owens et al. 1995, Randel y Welsh 2013). Se sabe que diferencias en las fases del crecimiento pueden presentar consecuencias a lo largo de la vida de la vaquilla, tanto a nivel productivo como reproductivo (Ford y Park 2001, Grings et al. 2007). Con base en lo anterior, el objetivo del presente estudio fue analizar el crecimiento de vacas Siboney con base en MNL; caracterizar la curva de crecimiento a partir de los parámetros de crecimiento derivados de los MNL; y, evaluar los efectos de los parámetros de crecimiento sobre la edad al inicio de la etapa reproductiva.
Materiales y métodos
Ajuste y selección de modelos no lineales
El estudio incluyó 10 064 datos de peso vivo, tomados en el intervalo de peso al nacer hasta 950 días de edad, de 2 021 vaquillas Siboney nacidas de 2005 a 2015; el número de pesadas por vaquilla osciló de dos a seis, con 4.9 pesadas promedio. Todas las vaquillas se desarrollaron en una empresa pecuaria, ubicada en el municipio Consolación del Sur de la provincia Pinar del Río, República de Cuba. El clima predominante es cálido tropical con dos estaciones, lluviosa de mayo a octubre, y seca de noviembre a abril. La temperatura media anual es de 24 oC , humedad relativa promedio del 80% con precipitaciones superiores a 3 000 mm anuales. El sistema de alimentación se basó en pastoreo; principalmente, Cynodon nlemfuensis, Digitaria decumbens y Panicum maximum; durante períodos poco lluviosos se suministró suplementación con Saccharum officinarum y Penisetum purpureum (Ribas et al. 2004, Evora et al. 2008)
Se evaluaron cuatro MNL: Logístico (LOG), Gompertz (GOM), Brody (BRO) y von Bertalanffy (BER); los cuales se describen en el Tabla 1, conformados por tres coeficientes de regresión que describen la curva de crecimiento (Agudelo et al. 2008, Domínguez-Viveros et al. 2013). Los análisis se realizaron con el método de Gauss-Newton y el procedimiento NLIN del programa para análisis estadístico SAS (SAS 2005). La selección del modelo con mejor ajuste se realizó en función del error de predicción promedio (EPP), la varianza del error de predicción (VEP), el estadístico de Durbin-Watson (DW), el coeficiente de determinación (R2), y los criterios de información de Akaike (AIC) y bayesiano (BIC) (Motulsky y Christopoulos 2003, Domínguez- Viveros et al. 2014, Tiago et al. 2017). Para EPP, VEP, AIC y BIC, el modelo con el menor valor se consideró como el de mejor ajuste; a diferencia del R2, el modelo con el valor más alto representa mejor ajuste. El DW analiza las auto correlaciones en los errores, con tres planteamientos: si 2 < DW ≤ 4 existe auto correlación negativa; si 0 < DW ≤ 2 revela ausencia de auto correlación; y, si DW < 0 indica que existe auto correlación positiva.
Tabla 1 Modelos no lineales evaluados y procedimientos de cálculo de los parámetros de crecimiento
| Modelo | EcuaciónÞ | EPI | PPI | GM |
| Brody | y = β1*(1- β2*е(-β3*t)) | -- | -- | (1- β2*(exp(-β3*t))) |
| Logístico | y = β1 / (1 + β2*e(-β3*t)) | t = ln β2 / β3 | y = β1 / 2 | 1/(1+ β2*(exp(-β3*t))) |
| Bertalanffy | y = β1*(1- β2*e(-β3*t))3 | t = ln 3 β2 / β3 | y = β1*8 / 27 | (1- β2*(exp(-β3*t)))3 |
| Gompertz | y = β1*(e(-β2*e(-β3*t))) | t = ln β2 / β3 | y = β1 * exp-1 | exp(-β2*(exp(-β3*t))) |
Þy = peso vivo a la edad t; t = edad de la vaquilla en días; β1 = peso adulto o asintótico en kg; β2 = constante de integración; β3 = pendiente de la curva, relativa a la tasa de crecimiento en kg/kg/t. EPI = edad al punto de inflexión en meses; PPI = peso al punto de inflexión en kg; GM = grado de madurez en porcentaje, a determinada edad.
Parámetros de crecimiento (PC) y sus efectos en la edad al primer empadre (EPE)
Con el modelo de mejor ajuste se realizó un análisis de regresión no lineal en las vaquillas con datos de seis pesadas; en 390 vaquillas se logró el criterio de convergencia obteniendo los tres coeficientes de regresión que conforman el MNL, todos estadísticamente diferentes de cero (p < 0.01). Posteriormente, para cada vaquilla se estimaron los PC (Tabla 1): a) peso adulto (PAD), a partir del valor asintótico del MNL; b) tasa de crecimiento (TAC), expresando la ganancia de peso como proporción del peso vivo; c) edad y peso (EPI y PPI) al punto de inflexión; d) grado de madurez en porcentaje a los 24 meses de edad (GM24); y, e) peso vivo a los 24 meses de edad (P24M), estimado con base en el MNL. Para analizar los efectos de los PC sobre la edad al primer empadre (EPE; años), se realizaron cuatro análisis de regresión lineal de orden cuadrático con base en los siguientes modelos: EPE = β1P24M +β2P24M2 +ε;EPE=β1TAC+β2TAC2 +ε;EPE= β1PPI + β2PPI2 + ε; y EPE = β1GM24 + β2GM242 + ε, donde β1 y β2 = coeficientes de regresión para el efecto lineal y cuadrático, respectivamente; ε = residuales. El análisis se realizó con el procedimiento REG de SAS (SAS 2005); para los cuatro modelos de regresión, con base en la primera derivada se obtuvo el punto de inflexión para determinar el punto de cambio en la pendiente de EPE sobre los PC.
Resultados y discusión
Con base en la VEP, AIC y BIC el modelo de mejor ajuste para describir el crecimiento fue BER, seguido de GOM, BRO y LOG (Tabla 2). El R2, mostró que todos los modelos explican más del 95% de la variabilidad en los datos. A partir del signo en el EPP los MNL tienden a sobre estimar las predicciones, y el DW exhibió que los residuales no presentan autocorrelaciones. El modelo BER presentó una curva sigmoidea (Figura 1) con PAD de 514.3 kg, el punto de inflexión representó el 29.6% del PAD, ubicado a los 5.93 meses de edad con 152.4 kg; la correlación negativa y alta entre TAC y PAD (Tabla 2) señala que las vaquillas con peso adulto alto no proceden de altas tasas de crecimiento. El modelo BER se ha reportado como de mejor ajuste para describir el crecimiento de vaquillas Holstein (Berry et al. 2005, Galvão et al. 2009); no obstante, Perotto et al. (1992) y Perotto et al. (1997) reportan como de mejor ajuste el modelo de Richards en el crecimiento de vaquillas Gyr, Guzerat y sus cruzas con Holstein. Las vaquillas en desarrollo representan la nueva generación del avance genético, por lo que es importante su incorporación a la vida reproductiva y productiva de manera idónea. La definición del peso corporal óptimo de las vaquillas en crecimiento depende del sistema de producción y del peso vivo de la vaca adulta a los cuatro años; para un crecimiento optimo, a los 6, 15 y 24 meses de edad la vaquilla debería alcanzar el 30, 60 y 90% del peso vivo adulto, respectivamente (Ballent et al. 2003, Roche et al. 2015). En vaquillas Siboney, con base en el modelo de BER (Figura 1), el peso vivo a los 6, 15 y 24 meses de edad representó el 16.7, 36.1 y 54.5% del PAD; el PAD de estos resultados coincide con la clasificación del biotipo liviano de la raza Holstein, y con la clasificación de mayor peso y tamaño de la raza Jersey (Ballent et al. 2003, Berry et al. 2005).
Tabla 2 Resultados para los coeficientes de regresión, parámetros de crecimiento y estadísticos en la selección de los modelos no lineales evaluados
| Modelo | Logístico | Brody | von Bertalanffy | Gompertz |
| β1 | 356.3±2.11 | 10003.7±6317.6 | 514.3±7.35 | 435.0±4.38 |
| β2 | 7.788±0.06 | 0.997±0.2 | 0.602±0.01 | 2.529±0.01 |
| β3 | 0.0047±0.0001 | 0.000035±0.0001 | 0.0016±0.0001 | 0.0024±0.0001 |
| rβ1-β3 | -0.84 | -0.99 | -0.98 | -0.95 |
| EPI | 7.4 | --- | 5.93 | 6.9 |
| PPI | 178.15 | --- | 152.4 | 160.0 |
| AIC | 64947.4 | 64818.9 | 64652.4 | 64679.4 |
| BIC | 64969.1 | 64840.5 | 64674.1 | 64701.0 |
| VEP | 634.5 | 626.7 | 616.2 | 617.8 |
| EPP | 5.60 | 2.91 | 4.41 | 5.48 |
| R2 | 0.97 | 0.96 | 0.98 | 0.97 |
| DW | 2.00 | 1.99 | 2.00 | 1.99 |
Coeficientes de regresión: β1 = peso asintótico en kg; β2 = constante de integración; β3 = pendiente de la curva, o tasa de crecimiento en kg/kg/t; rβ1-β3 = correlación entre β1 y β3. Edad (EPI; meses) y peso (PPI; kg) al punto de inflexión. EPP = error de predicción promedio; VEP = varianza del error de predicción; DW = estadístico de Durbin-Watson; R2 = coeficiente de determinación; AIC = criterio de información de Akaike; BIC = criterio de información Bayesiano.
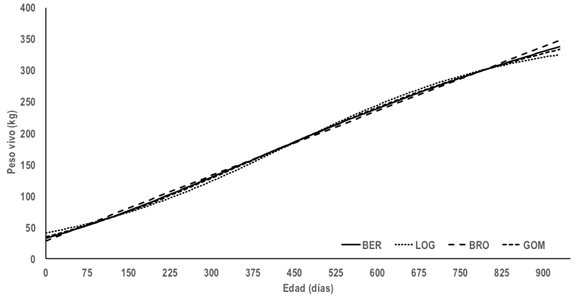
Figura 1 Curvas de crecimiento de vaquillas Siboney con base en los modelos no lineales de von Bertalanffy (BER), logístico (LOG), Brody (BRO) y Gompertz (GOM)
La EPE promedio fue de 2.2 ± 0.26 años, con promedio de 333.6 ± 9.52 kg. Los resultados del análisis de regresión fueron: EPE = (0.026102)(P24M) - (0.0000636)(P24M2 ); EPE = (23.86)(TAC) - (59.17)(TAC2 ); EPE = (0.0796)(GM24) - (0.000675)(GM242 ); y, EPE = (0.0299)(PPI) - (0.00009506)(PPI2); en todos los casos los coeficientes de regresión fueron estadísticamente diferente de cero (p < 0.01) y el coeficiente de determinación fue igual o superior a 0.95. Las cuatro ecuaciones de regresión tuvieron comportamiento similar, al inicio la EPE incrementó junto con la variable de crecimiento evaluada hasta el punto de inflexión o cambio del signo en la pendiente, con valores de 205.2 kg en P24M, 0.2016% en TAC, 58.9% en GM24 y 157.3 kg en PPI; a partir del punto de inflexión por cada unidad de incremento en los PC se observaron efectos para reducir EPE; en la Figura 2 se presenta el comportamiento de la EPE a través del P24M.
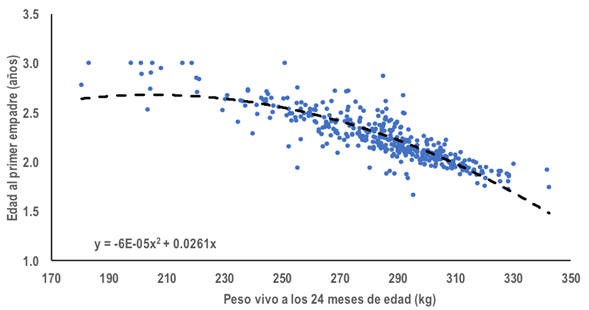
Figura 2 Relación de la edad al primer empadre y el peso vivo a los 24 meses de edad, producto del análisis de regresión lineal de orden cuadrático
La edad puede ser un modulador significativo del inicio de la pubertad, siempre y cuando los animales estén en un plano nutricional adecuado en las primeras fases del desarrollo. El inicio de la fase reproductiva es un proceso presidido por una señal nutricional, el cerebro requiere reconocer cierto grado de desarrollo corporal y madurez para iniciar las funciones del mecanismo fisiológico que controlan la reproducción, lo cual sustenta el criterio de que el tamaño corporal es más importante que la tasa de crecimiento, dado que el crecimiento y conformación del aparato reproductor constituyen un proceso gradual que requiere de cierto grado de madurez del animal (Placen et al. 1998, Foster y Nagatani et al. 1999). Otros autores han propuesto que la pubertad ocurre en el punto de inflexión de la curva de crecimiento, en ese punto se realiza un cambio en la tasa de crecimiento y en la tasa de deposición de tejido magro a tejido graso, asociando el retraso de la pubertad a una menor deposición de grasa (Randel y Welsh 2013); el tejido adiposo desempeña un papel importante en los mecanismos que regulan los factores de crecimiento y las hormonas reproductivas (Zieba et al. 2005, Hausman et al. 2012). Las vaquillas pueden alcanzar la pubertad a un peso similar, pero no ocurre con una composición corporal o estado metabólico y endocrino similar (Hall et al. 1995).
Con el manejo y alimentación de la vaquilla en crecimiento se debe planear un peso y desarrollo corporal adecuado para el primer parto, con la intensión de evitar repercusiones en el rendimiento por lactancia y la longevidad o vida productiva de la vaca. El modelo de von Bertalanffy fue el de mejor ajuste para describir el crecimiento de las vaquillas Siboney, presentó una curva sigmoidea con punto de inflexión a los 5.93 meses de edad con 152.4 kg. Los parámetros de crecimiento mostraron efecto sobre la edad al primer empadre y al inicio una pendiente positiva, a partir de este punto de cambio se observaron efectos para reducir la edad de inicio de la etapa reproductiva.











 nueva página del texto (beta)
nueva página del texto (beta)



