Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista ALCONPAT
versão On-line ISSN 2007-6835
Rev. ALCONPAT vol.12 no.3 Mérida Set./Dez. 2022 Epub 08-Abr-2024
https://doi.org/10.21041/ra.v12i3.592
Investigación básica
Evaluación de la influencia de la corrosión en la estabilidad global de las columnas de hormigón armado
1 Fundação Hermínio Ometto (FHO | Uniararas), Araras, Brasil.
² Universidade Federal Tecnológica do Paraná (UTFPR), Curitiba, Brasil.
Este trabajo analiza el impacto de la corrosión en la estabilidad global de las columnas de hormigón armado, evaluando la efectividad de los criterios de reducción de rigidez propuestos por la ABNT NBR 6118: 2014. Con los análisis, utilizando modelos de elementos finitos que reproducían el comportamiento de los materiales, se definió que la corrosión provoca la intensificación de los esfuerzos globales de segundo orden en la estructura. Sin embargo, en situaciones críticas, la pérdida de equilibrio en la sección transversal resultó en una falla estructural incluso antes de la pérdida de la estabilidad. El estudio se llevó a cabo tanto a través de un análisis geométrico no lineal como mediante la aplicación del coeficiente γz, donde se concluyó que la posterior adición de efectos reológicos puede conducir a una configuración que va más allá de los límites propuestos por la norma brasileña.
Palabras clave: hormigón; corrosión; estabilidad global; efectos de segundo orden
This paper analyzes the impact of corrosion on the global stability of reinforced concrete columns, evaluating the effectiveness of the stiffness reduction criteria proposed by ABNT NBR 6118:2014. It was defined through finite element models that corrosion causes the intensification of the second-order effects. However, in critical situations, the failure in the transversal section led to structural collapse even before the stability loss. The study was conducted through nonlinear geometric analyses and applying the γ z coefficient. It was concluded that the subsequent addition of rheological effects could exceed the limits proposed by the ABNT NBR 6118:2014.
Keywords: concrete; corrosion; global stability; second-order effects
Este trabalho analisa o impacto da corrosão na estabilidade global de colunas em concreto armado, avaliando a eficácia dos critérios de redução de rigidez propostos pela ABNT NBR 6118:2014. A partir das análises, utilizando-se modelos em elementos finitos que reproduziram o comportamento dos materiais, definiu-se que a corrosão causa a intensificação dos esforços globais de segunda ordem na estrutura. Entretanto, em situações críticas, a perda de equilíbrio na seção transversal conduziu à falha estrutural antes mesmo da perda de estabilidade. O estudo foi realizado tanto por meio de uma análise não-linear geométrica, quanto pela aplicação do coeficiente γz, onde concluiu-se que a posterior adição de efeitos reológicos pode conduzir a uma configuração que ultrapasse os limites propostos pela norma brasileira.
Palavras-chave: concreto; corrosão; estabilidade global; efeitos de segunda ordem
1. Introducción
La corrosión puede entenderse como la interacción destructiva entre el material y el ambiente en el que se encuentra, desencadenada por acciones electroquímicas, químicas, físicas o por la unión de estas, constantemente provocada por la acción de los cloruros o por el desarrollo de fisuras. La presencia de corrosión en regiones con tensiones de tracción es la situación más grave, ya que puede provocar la ruptura frágil de la sección sin deformación previa de la estructura (Helene, 1993; Schvartzman et al., 2010).
Las armaduras de acero en el interior del hormigón están protegidas por una película de óxido de hierro que se forma en la superficie del metal debido a la alcalinidad del hormigón, asegurando su pasivación. Sin embargo, esta película puede tener su integridad comprometida con la reducción del pH por debajo de nueve, resultado de la carbonatación del hormigón en la capa de recubrimiento, que se produce debido a la presencia de iones cloruro, en índices críticos de contaminación atmosférica o con la lixiviación del hormigón, pudiendo ser intensificados por condiciones adversas del medio ambiente, tipo o edad de la construcción (Maldonado-Bandala et al., 2018; Araujo et al., 2020; Silvestro et al., 2020).
El uso de espesores inadecuados en el recubrimiento, debido a errores de diseño o ejecución, puede comprometer la protección necesaria para mantener la integridad de las barras de acero (Fusco, 2008; Malheiro et al., 2014; Felix y Carrazedo, 2021). Además, la elección del cemento, aditivos y adiciones puede mitigar o intensificar el potencial corrosivo (Silva et al., 2015; Trevisol et al., 2017; Dietrich et al., 2017; Teixeira et al., 2021).
La corrosión del acero resulta en un hidróxido débil, pulverulento, sin adherencia o cohesión llamado óxido, que aumenta su volumen a medida que se forma y puede alcanzar de ocho a diez veces el volumen de acero del que se originó. Las partículas oxidadas presionan el hormigón circundante, desencadenando la degradación de la estructura. (Verçoza, 1991; Balestra et al., 2018).
Varios estudios buscan reproducir las condiciones de deterioro en el laboratorio a través de pruebas aceleradas (Meira y Ferreira, 2019), otros buscan investigar el impacto que diferentes adiciones tienen sobre el hormigón con respecto a su potencial corrosivo (Amorim Júnior et al., 2021; Santos et al., 2020; Blanco et al., 2019; Figueiredo et al., 2014). Tales esfuerzos se vuelven cada vez más necesarios, ya que la estimación de principios de este siglo señaló que hasta el 3,5% del producto interno bruto de un país desarrollado se reinvierte para contornear los efectos de la degradación por corrosión (Mackechnie y Alexander, 2001). Delante de eso, las inversiones en modelos matemáticos que puedan describir la degradación estructural causada por la corrosión están aumentando.
Investigaciones recientes han explorado la simulación numérica de la difusión de cloruros en hormigón, como los trabajos de Ayinde et al. (2017) y Souza y Leonel (2021), o a través de análisis de confiabilidad basados en modelos probabilísticos (Felix et al., 2020; Ramos y Carrazedo, 2021; Favretto et al., 2021). Otras aplicaciones utilizan el método de los elementos finitos, como la propuesta por Ramos y Carrazedo (2020), quienes desarrollaron modelos capaces de describir las diferentes fases del hormigón armado y la propagación del daño causado por el proceso corrosivo.
Por lo tanto, el presente trabajo busca contribuir a esta área del conocimiento, agregando al problema la evaluación de la estabilidad global de una estructura degradada. Para ello, se reprodujo numéricamente el comportamiento mecánico del hormigón, así como la evolución del daño cuando se somete a cargas externas y a la corrosión de la armadura. Tal modelo fue construido con la aplicación del Método de los Elementos Finitos (MEF), como se discutió a lo largo del trabajo.
2. Procedimiento
El uso de simulaciones numéricas para predecir el comportamiento de estructuras de hormigón armado, en presencia de daños, requiere una reproducción satisfactoria del comportamiento mecánico de los materiales constituyentes frente a solicitudes externas. Para ello, se definieron modelos constitutivos que caracterizan los materiales en los análisis realizados. En este apartado se describirán todos los parámetros utilizados para simular el comportamiento mecánico del hormigón armado, así como la validación de los modelos constitutivos utilizados.
2.1 Modelos constitutivos de los materiales
A los elementos modelados se añadieron materiales que reproducen el comportamiento del acero y el hormigón, conteniendo características como la densidad, el módulo de elasticidad y el coeficiente de Poisson.
En el caso del hormigón, debido al desarrollo natural de las fisuras, fue necesario añadir más información para que el material reproduzca fielmente su comportamiento a la tracción, compresión, acumulación de deformaciones inelásticas y daños.
Los modelos constitutivos utilizados en los materiales, hormigón y acero, fueron extraídos del código europeo CEB-FIB (2010). Así, el propósito principal de esta etapa es la reproducción del comportamiento mecánico del hormigón armado, de su curva tensión x deformación, incluida la influencia de la aplicación de un modelo de daño.
2.1.1 Modelo constitutivo del acero
El modelo constitutivo utilizado para el acero caracteriza su comportamiento en presencia de tensiones de tracción, representado en el diagrama de la Figura 1, o compresión. El primer tramo representa la respuesta lineal del material hasta alcanzar el valor característico de la resistencia al flujo del acero en tracción (f yk ), seguido de un segundo tramo lineal que corresponde a su flujo con el endurecimiento hasta alcanzar el valor característico de la resistencia a la tracción del acero (f tk ), que se produce en el valor característico de deformación máxima (ε uk ).
Las tensiones en el acero (σ s ) se obtuvieron mediante la Ecuación (1), con los valores del módulo de elasticidad del acero (E s ) y la deformación del acero (ε s ).
dónde:
2.1.2 Modelo constitutivo del hormigón
El modelo constitutivo utilizado en el hormigón caracteriza su comportamiento diante de las solicitudes de compresión (Figura 2), y tracción (Figura 3 y Figura 4).
Al comprimirse, el hormigón presenta un comportamiento elástico hasta alcanzar su valor medio de resistencia a la compresión (f cm ), pasando a perder rigidez. A partir de este punto, el desarrollo de microfisuras provoca el ablandamiento del material, representado en la sección decreciente del diagrama.
El hormigón traccionado presenta un comportamiento elástico lineal hasta alcanzar la deformación de tracción del hormigón (ε ct ) de 0,15‰. En aproximadamente el 90% del valor promedio de la resistencia a la tracción axial del hormigón (f ctm ), el desarrollo de microfisuras causa una disminución en la rigidez del material, caracterizando una zona de fisuración. En tensiones cercanas a lo f ctm el cuadro se intensifica, una vez que ocurre la evolución de las fisuras. A partir de este punto, el material sufre una reducción drástica en su rigidez.
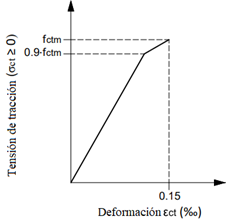
Figura 3 Diagrama tensión x deformación del hormigón traccionado en régimen elástico (Adaptado de CEB-FIB, 2010)
El f cm se definió a través de la Ecuación (2), a partir del valor característico de la resistencia a compresión del concreto (f ck ) y el valor estandarizado que representa la diferencia entre la resistencia promedio del concreto y su resistencia característica (∆ f ).
El módulo secante desde el origen hasta el pico de la tensión de compresión (E C1 ) se definió mediante la ecuación (3). En esta ecuación se utilizaron las deformaciones a compresión del hormigón (ε c ), que van desde cero hasta la deformación final en compresión (ε c,lim ) de 3,5‰, y la deformación por compresión máxima (εc1), obtenida a través de los valores de tabla contenidos en el CEB-FIB (2010).
Se utilizó la Ecuación (4) para determinar el módulo de elasticidad del concreto a los 28 días (E ci ), el cual depende del módulo de elasticidad tangente inicial (E c0 ), el parámetro en función de la naturaleza del agregado (α E ) y el valor estandarizado (∆ f ), definido en consulta con CEB-FIB (2010).
El valor de la relación entre las deformaciones (η) y la constante de plasticidad (k) se definió mediante la Ecuación (5) y la Ecuación (6), respectivamente. Finalmente, se utilizó la Ecuación (7) para calcular los valores de tensión de compresión del hormigón (σ c ) y obtener la ley tensión x deformación que se presenta en el diagrama de la Figura 2.
La resistencia a la tracción axial del hormigón (f ctm ) se definió a través de la Ecuación (8) y la Ecuación (9), de acuerdo con su f ck .
En la zona de fractura, las tensiones y deformaciones se relacionan con una abertura de fisuras ficticia (w), y sus valores en puntos específicos, (w 1 ) y (w c ), se obtienen a través de la Ecuación (10) y la Ecuación (11), respectivamente. Finalmente, la energía de fractura (G F ) se obtuvo a través de la ecuación (12).
Vale señalar que solo conocer la apertura de fisuras en función de la energía de fractura no es suficiente para muchas aplicaciones. Así, Aitsin et al. (2008) aportan la definición de la longitud característica (l ch ), un valor útil para la evaluación de la apertura de fisuras en cuanto a la deformación. Esta grandeza se obtiene de la Ecuación (13).
Las deformaciones específicas (ε t ) tenían sus valores que iban desde cero hasta el valor final de la apertura de fisuras ficticia (w c ), convertido a partir de la razón entre w c y l ch . Los valores de tensión de tracción (σ t ) se definieron hasta una deformación de 0,15‰ mediante la Ecuación (14) y la Ecuación (15), conforme el f ctm . En la zona de fractura, los valores de σ t se determinaron utilizando la Ecuación (16) y la Ecuación (17), en un intervalo que varió de 0,15‰ a w c .
Al final de los cálculos, los valores de σ c y σ t se agregaron al modelo de daño aplicado al material que representa el hormigón en las simulaciones numéricas realizadas.
2.1.2.1 Modelo de daño aplicado al hormigón
El modelo adoptado para el hormigón fue el Concrete Damage Plasticity (CDP), un modelo de daño con plastificación desarrollado por Lubliner et al. (1989) y perfeccionado por Lee y Fenves (1998). Dicho modelo está implementado y disponible en el software Abaqus®.
Para este modelo de material, el comportamiento en presencia de daño se representa en los diagramas de la Figura 5 y la Figura 6 y se describe matemáticamente por las leyes tensión x deformación indicadas en la Ecuación (18), para la compresión, y la Ecuación (19), para la tracción, propuestas por Hibbitt et al. (2011).
Tanto en tracción como en compresión, mientras está intacto, el hormigón muestra conservación en su módulo de elasticidad inicial (E 0 ). Cuando se alcanza la máxima tensión en tracción (σ tu ) o en compresión (σ cu ), se inicia el proceso de degeneración de este módulo de elasticidad a medida que se incrementan las variables de daño d t (tracción) y d c (compresión). Las deformaciones plásticas en tracción ε t pl y en compresión ε c pl incorporan la plastificación en el modelo.
Las variables de daño d c y d t se obtuvieron mediante la Ecuación (20) y la Ecuación (21), respectivamente, propuestas por Yu et al. (2010), con los valores de σ c , σ t , f cm y f ctm ya definidos anteriormente.
Finalmente, los valores de las variables de daño d c y d t , obtenidos con los cálculos, se agregaron al modelo de daño del hormigón.
2.2 Validación de los modelos constitutivos
Con el fin de analizar si los modelos constitutivos utilizados en la caracterización de los materiales garantizan el comportamiento esperado, se realizaron simulaciones numéricas en el software Abaqus®. En esta primera etapa se realizaron tres análisis, uno para verificar el comportamiento del acero traccionado, en un elemento de barra bidimensional, y los otros dos para verificar el comportamiento del hormigón traccionado y comprimido, en un elemento sólido bidimensional. Los modelos constitutivos validados se aplicaron en una simulación numérica no lineal de una viga de hormigón armado. Para ello se realizó un modelado 3D en Abaqus®, utilizando elementos sólidos paralelepipédicos lineales de 8 nodos (simulando el hormigón) y elementos de barra 3D (simulando las barras de acero y los estribos). Se consideró una perfecta adherencia entre el acero y el hormigón.
Los resultados obtenidos con las simulaciones numéricas fueron comparados con los modelos teórico-analíticos propuestos en el CEB-FIB (2010), siendo representados en la Figura 7, Figura 8 y Figura 9.
Con los análisis, se pudo definir que el modelo constitutivo utilizado en la modelización numérica del acero garantizaba el comportamiento esperado, presentando solo un desvío sutil al inicio del tramo que representa su flujo con el endurecimiento. En cuanto al hormigón, los análisis permitieron observar que el material numéricamente representado simulaba satisfactoriamente el comportamiento previsto, presentando solo variaciones modestas en las zonas de falla y fractura.
Los modelos constitutivos validados se aplicaron en la simulación numérica no lineal de una viga de hormigón armado sujeta a la aplicación de cargas. Para ello, se realizó un modelado tridimensional, utilizando elementos sólidos paralelepédicos lineales de 8 nodos, simulando el hormigón, y elementos tridimensionales de barras de acero, representando las barras y estribos, en el software Abaqus®. Se consideró una perfecta adherencia entre el acero y el hormigón, obtenida mediante el empotramiento de las barras de acero en el elemento de hormigón.
Las dimensiones, la tasa de refuerzo, el lugar de aplicación de las cargas sobre la viga y las propiedades elásticas de los materiales, Tabla 1, fueron registradas por Álvares (1993). La malla estructurada de elementos finitos aplicada en el modelo pasó por pruebas de convergencia, mediante la realización de análisis lineales iterativos, aumentando el número de elementos, hasta que el desplazamiento en el centro de la viga dejó de sufrir cambios.
Tabla 1 Propiedades elásticas de los materiales (Adaptado de Álvares, 1993)
| Material | Coeficiente de Poisson | Módulo de Young (MPa) |
|---|---|---|
| Hormigón | 0.2 | 29200 |
| Acero | 0.3 | 196000 |
El análisis se realizó hasta un desplazamiento de 8 mm en el centro de la viga, correspondiente a una carga P de aproximadamente 47 kN. A medida que se realizaba la aplicación progresiva de las cargas, en forma de desplazamientos prescritos, se registraban los desplazamientos en el centro de la viga.
Finalmente, se compararon los resultados con los obtenidos en el análisis experimental de Álvares (1993) y con el modelo teórico deducido por los autores, a partir de las hipótesis de fisuración propuestas por Branson (1968). El modelo de Branson (1968) permite la consideración de una inercia media, que tiene en cuenta los efectos de la fisuración a lo largo del tramo del elemento estructural, a partir de un análisis semiprobabilístico. Tales comparaciones se representan en la Figura 10.
La viga de la simulación numérica se comportó de manera similar al análisis experimental y al modelo analítico en los Estadios I y II. Se observaron divergencias sutiles, pero se justifican por las incertidumbres asociadas a los parámetros de caracterización del hormigón. Además, existen divergencias sensibles entre las condiciones de contorno adoptadas en el modelo numérico y las presentes en el ensayo experimental.
Con la simulación numérica, también fue posible observar la evolución del daño en la estructura, representado en la Figura 11. Ocurrió el desarrollo y propagación de fisuras en el elemento conforme la aplicación de las cargas, hasta alcanzar un alto estado de degradación, de forma muy similar a lo observado por Álvares (1993) en su análisis experimental.
Después de confirmar la eficiencia de los modelos constitutivos aplicados, así como el modelo de daño utilizado para representar la degradación del hormigón, se realizó el modelado de una estructura en el software Abaqus®, donde se agregó la corrosión a los análisis como se discutirá en las siguientes secciones.
2.3 Modelado de la estructura sujeta a corrosión
En esta etapa, se presentará la idealización de la estructura estudiada, la estrategia para a simulación numérica de la degradación causada por el fenómeno de corrosión en los refuerzos y la metodología para la evaluación de la estabilidad global. También se dará información sobre la construcción del modelo en elementos finitos con el fin de permitir la reproducibilidad de la investigación.
2.3.1 Características geométricas de la estructura
La estructura escogida para las simulaciones se basa en la presentada por Wahrhaftig (2008), Figura 12. Se trata de una estructura de sección hueca y esbelta en hormigón armado, utilizada como soporte para un sistema de transmisión telefónica. Aunque las dimensiones reproducidas en el modelo numérico no son las mismas que las de la estructura real, se mantuvo la proporción del índice de esbeltez de la estructura. Así, el elemento estructural fue modelado con una altura de 14 metros y está armado con 16 barras de acero de 25 mm, dispuestas según la Figura 12.
Tanto la estructura de hormigón como las barras de acero fueron modeladas con elementos sólidos lineales paralelepipédicos de 8 nudos. Las condiciones de contorno aplicadas en el modelo están compuestas por una carga vertical puntual de 5 kN, posicionada en la parte superior del elemento, como representación de las antenas, y por un engaste, posicionado en la base del elemento, ambos añadidos en el punto central de la sección. Además, las fuerzas horizontales que caracterizan la acción del viento se agregaron al modelo en forma de cargas puntuales cada 1 metro de la estructura. Finalmente, se consideró el peso propio para una gravedad de 9,81 m/s, con las masas específicas de hormigón y acero, extraídas de la ABNT NBR 6120:2019, iguales a 2400 kg/m³ y 7850 kg/m³, respectivamente.
2.3.2 Estimación del viento
El viento fue estimado a través de ecuaciones extraídas de la ABNT NBR 6123:1988 y aplicadas a la estructura como fuerzas puntuales horizontales, en cada metro, en el lado izquierdo del elemento estructural.
Inicialmente, se calculó el valor del factor S 2 , que considera la influencia de la rugosidad del terreno, las dimensiones de la edificación y su altura sobre el terreno, a través de la Ecuación (22). Con el valor del factor topográfico S 1 , considerando el terreno plano o ligeramente accidentado, el factor calculado S 2 , el factor estadístico S 3 , considerando una edificación cuya ruina total o parcial pueda afectar la seguridad o posibilidad de socorro de las personas después de una tormenta destructiva, y de la velocidad básica del viento (V 0 ), definida en función de la ubicación de la estructura. La velocidad básica del viento es una grandeza necesaria para la determinación de la velocidad característica del viento, V k (Ecuación (23)).
Así, después de estas definiciones, se calculó la presión dinámica (q), utilizando la Ecuación (24), este valor es útil para calcular las fuerzas puntuales añadidas al modelo.
Por lo tanto, se calculó la fuerza de arrastre (F a ), Ecuación (25), con los valores del coeficiente de arrastre (C a ), el factor de reducción (K), la distancia vertical entre las fuerzas (H) y el diámetro externo de la sección (D). Tales valores de F a , calculados en cada metro, corresponden a la intensidad de las fuerzas horizontales aplicadas en la estructura.
dónde
dónde
dónde
2.3.3 Adición de la corrosión
La corrosión se agregó al modelo para verificar su influencia en la estabilidad de la estructura. La expansión generada por los productos de la corrosión se representó mediante la aplicación de desplazamientos radiales prescritos en extensiones preestablecidas del hormigón en contacto con las barras de acero afectadas por la corrosión, posicionándose en la región más afectada por la acción del viento en la estructura. El método utilizado para definir los valores de los desplazamientos radiales aplicados fue propuesto por El-Maaddawy y Soudki (2007).
La constante de flexibilidad del agujero (k) se obtuvo mediante la Ecuación (26). Es una constante que relaciona el desplazamiento radial con la presión de corrosión, teniendo en cuenta la zona porosa presente en la interfaz de contacto entre el acero y el hormigón, que debe ser inicialmente rellenada por los productos de la corrosión antes de que las tensiones expansivas generadas comiencen a crear presión sobre el hormigón circundante. Para esto, se utilizaron los valores del coeficiente de Poisson (ν), el módulo de elasticidad efectivo (E ef ), el diámetro de las barras de acero (D), el espesor de la zona porosa (δ 0 ), que oscila entre 10 y 20 μm, y el factor (Ψ) calculado con la Ecuación (27), que tiene en cuenta el recubrimiento de hormigón (C).
La presión radial necesaria para producir desplazamientos en el hormigón (P cor ) se calculó mediante la Ecuación (28), donde el valor porcentual de pérdida de masa del acero (m 1 ) varió de acuerdo con la clase de resistencia del hormigón. Finalmente, fue posible definir los valores de desplazamiento en lo hormigón (δ c ) necesarios para acomodar el aumento de volumen debido a la transformación del acero en óxido, a través de la Ecuación (29).
El porcentaje de pérdida de masa de acero (m 1 ) se puede relacionar con la masa de acero consumida por unidad de longitud (M loss ) a través de la Ecuación (30), con los valores del diámetro de las barras de acero (D) y la densidad del acero (ρ s ).
2.4 Metodología para el estudio de la estabilidad global
Inicialmente, se realizaron tres simulaciones en el software Abaqus®, con el fin de verificar la estabilidad de la estructura con diferentes clases de resistencia de hormigón, que van desde C20 hasta C50. El valor del desplazamiento en la parte superior y el momento en la base de la estructura se verificaron en cada análisis realizado.
La primera etapa consistió en el cálculo del coeficiente γ z según la ABNT NBR 6118:2014, Ecuación (31), con los valores de desplazamiento en cada metro de la estructura, medidos en el primer análisis (AN1), o sea, un análisis elástico y lineal con reducción del módulo de elasticidad (E) en un 20% (de acuerdo con el ítem 15.7.3 de la ABNT NBR 6118:2014).
El coeficiente γ z permite evaluar la importancia de los esfuerzos globales de segundo orden en la estructura y su clasificación en función de la dislocación de los nodos, considerando una estructura de nodos fijos aquella cuyo valor de γ z es menor o igual a 1,1. Este coeficiente depende del momento de volteo y de la suma de los productos de todas las fuerzas verticales por los desplazamientos horizontales de sus respectivos puntos de aplicación, obtenidos en el análisis de 1º orden.
Luego, se agregó la No Linealidad Geométrica (NLG) al modelo AN1, dando lugar al segundo análisis (AN2), donde la reducción del módulo de elasticidad se mantuvo en un 20%.
Con los valores de momento en la base, obtenidos en el primer y segundo análisis (AN1 y AN2), se calculó un nuevo coeficiente γ z . Esta vez, el ∆M tot,d utilizado fue la diferencia entre el momento obtenido en el segundo y en el primer análisis, mientras que el valor de M 1,tot,d fue el del momento del primer análisis (AN1). Este cálculo solo ratificó la competencia del coeficiente γ z como estimador de los efectos de segundo orden.
Finalmente, en el tercer análisis (AN3), el valor de E se mantuvo intacto y se agregaron al modelo la No Linealidad Física (NLF) y NLG. El coeficiente γ z , ahora renombrado γ zcalc , Ecuación (32), fue calculado y será presentado en los resultados de esta investigación.
En esta etapa, el NLF se sumó a las simulaciones a través de los modelos constitutivos de los materiales y el modelo de daño, reemplazando la reducción del módulo de elasticidad en un 20% de los modelos AN1 y AN2.
Posteriormente, se agregó la corrosión al modelo del tercer análisis y se realizaron ocho simulaciones más con cada clase de concreto. Los cuatro primeros análisis se realizaron en um modelo afectado por la corrosión en tres de sus dieciséis barras de acero, en una extensión de 5 cm (AN4 a AN7). Los demás se realizaron en un modelo con acción de la corrosión en cinco de sus dieciséis barras de acero, en una extensión de 10 cm (AN8 a AN11).
Dónde
Dónde
En ambos casos, la corrosión se agregó a una distancia de 30 cm de la base del elemento, siendo esta la región de máximo momento provocado por la acción del viento. En esta etapa, el coeficiente γ zcalc se calculó como se describe en la Ecuación (32).
El resumen de los análisis realizados se encuentra en el Cuadro 1. Además, es importante destacar que en todos los análisis la adherencia entre el acero y el hormigón se consideró perfecta, con la excepción de las regiones degradadas por la corrosión.
Cabe señalar que se puede consultar información adicional sobre el coeficiente γ z , incluida su deducción matemática, en el trabajo de Franco y Vasconcelos (1991).
Cuadro 1 Resumen de los análisis realizados
| Análisis | Características | |
|---|---|---|
| AN1 | Análisis lineal físico y geométrico, con una reducción del 20% en el módulo de elasticidad | LF, LG y 0.8E |
| AN2 | Análisis lineal físico, no lineal geométrico, con una reducción del 20% en el módulo de elasticidad | LF, NLG y 0.8E |
| AN3 | Análisis no lineal físico y geométrico, sin reducción del módulo de elasticidad | NLF, NLG y E |
| AN4 a AN11 | Análisis no lineal físico y geométrico, sin reducción del módulo de elasticidad, con la adición de la corrosión | NLF, NLG, E y corrosión |
2.4.1 Malla de elementos finitos
La malla de elementos finitos añadida al modelo fue compuesta por elementos tridimensionales paralelepipédicos lineales, por tanto, formados por 6 caras y 8 nodos.
La convergencia de la malla aplicada al modelo se realizó a través de simulaciones iterativas, sin la consideración de no linealidades, aumentando el número de elementos finitos que componen la malla, hasta que el valor del desplazamiento en la parte superior de la estructura dejó de sufrir cambios.
3. Resultados y discusión
La corrosión se agregó gradualmente al modelo, de modo que el desplazamiento aplicado fue mayor en cada simulación realizada con cada clase de resistencia del hormigón, a medida que aumentaba el porcentaje de corrosión (m 1 ). La equivalencia entre los valores de m 1 , el desplazamiento radial aplicado en el hormigón (δ c ) y la masa de acero consumida por unidad de longitud (M loss ) utilizados en las simulaciones se representan en la Tabla 2.
Tabla 2 Resumen de los parámetros utilizados en las simulaciones
| Análisis | C20 e C30 | C40 e C50 | |||||
|---|---|---|---|---|---|---|---|
| m1 [%] | Desplazamiento radial, δc [μm] | Mloss [g/m] | m1 [%] | Desplazamiento radial, δc [μm] | Mloss [g/m] | ||
| 3 barras | AN3 | 0.091 | 0.00 | 3.51 | 0.091 | 0.00 | 3.51 |
| AN4 | 0.150 | 8.13 | 5.79 | 0.300 | 28.75 | 11.57 | |
| AN5 | 0.200 | 15.00 | 7.72 | 0.350 | 35.63 | 13.50 | |
| AN6 | 0.250 | 21.88 | 9.65 | 0.400 | 42.51 | 15.43 | |
| AN7 | 0.300 | 28.75 | 11.57 | 0.450 | 49.38 | 17.36 | |
| 5 barras | AN3 | 0.091 | 0.00 | 3.51 | 0.091 | 0.00 | 3.51 |
| AN8 | 0.105 | 1.94 | 4.05 | 0.125 | 4.69 | 4.82 | |
| AN9 | 0.110 | 2.63 | 4.24 | 0.138 | 6.41 | 5.31 | |
| AN10 | 0.115 | 3.31 | 4.44 | 0.150 | 8.13 | 5.79 | |
| AN11 | 0.120 | 4.00 | 4.63 | 0.163 | 9.85 | 6.27 | |
Con las simulaciones se pudo verificar que los dos parámetros analizados, desplazamiento en la parte superior y momento en la base de la estructura, aumentaron con el incremento de m 1 , demostrando que la evolución de la corrosión en el refuerzo genera una reducción en la rigidez de la estructura, provocando la intensificación de sus reacciones con motivo del incremento de los esfuerzos de segundo orden. Los valores de los momentos en la base de la estructura, obtenidos con las simulaciones, se muestran en la Figura 13.
La Tabla 3 muestra los valores calculados de γ zcalc para las simulaciones AN1, AN3 y para las simulaciones AN7, realizadas después de la adición de la corrosión, considerando todas las clases de hormigón analizadas. Los valores presentados para las simulaciones con adición de la corrosión fueron los obtenidos aplicándola en 3 barras de acero del modelo, ya que alcanzó valores superiores de γ zcalc en comparación con la aplicación en 5 barras.
Tabla 3 Coeficiente γzcalc
| Clase de hormigón | AN3 | AN7 | AN1 (NBR 6118:2014) | Relación entre AN7 y AN1 [%] |
|---|---|---|---|---|
| C20 | 1.0293 | 1.0302 | 1.0348 | 99.56 |
| C30 | 1.0276 | 1.0284 | 1.0330 | 99.56 |
| C40 | 1.0246 | 1.0260 | 1.0298 | 99.63 |
| C50 | 1.0237 | 1.0249 | 1.0287 | 99.63 |
Los valores calculados de los coeficientes γ zcalc están relacionados con los valores de m 1 en la Figura 14. Es posible observar que en todas las clases de resistencia del hormigón, en ambas situaciones de corrosión propuestas, el γ zcalc aumenta con el aumento de m 1 y, en consecuencia, del desplazamiento radial causado por la corrosión, δ c .
Al analizar los resultados presentados en la Tabla 3 y la Figura 14, se observa que la adición de la corrosión a la simulación generó un aumento en el valor del coeficiente γ zcalc en todas las clases de resistencia del hormigón analizadas. Teniendo en cuenta que el γ zcalc se puede adaptar a un coeficiente de mayoración de los esfuerzos globales de 1º orden, provenientes de las cargas horizontales, es posible definir que la adición de la corrosión provocó la intensificación de los esfuerzos globales de 2º orden en la estructura.
Al relacionar los valores de γ zcalc obtenidos en la AN7 y AN1, fue posible definir que los efectos de segundo orden en la estructura con la adición de la corrosión corresponden a aproximadamente el 99,6% de los determinados por la NBR 6118:2014, en todas las clases de resistencia del hormigón. Así, los valores obtenidos con base en la norma fueron superiores, demostrando que la reducción de rigidez propuesta por la norma brasileña es capaz de acomodar el nivel de corrosión evaluado en este trabajo.
Además, se observó que los hormigones con menor resistencia sufren más la acción de la corrosión, ya que presentaban valores mayores de γ zcalc . Los hormigones con un f ck mayor, incluso sometidos a valores mayores de m 1 , presentaron resultados menores de γ zcalc , demostrando una mayor resistencia a las acciones externas y a la degradación.
La Figura 15, tomada del software Abaqus® después de realizar las simulaciones numéricas, trae un conjunto de imágenes de la sección transversal de la estructura analizada, en la región donde se agregó la corrosión, en 3 y 5 barras de acero, con el hormigón C40. Es posible observar la evolución de las fisuras en el hormigón alrededor de las barras de acero a medida que aumenta el producto de la corrosión. La Figura 15 muestra el daño generado por las tensiones de tracción, medido a través de la variable DAMAGET (grandeza adimensional).
Con la evolución del daño, la convergencia numérica se ve afectada, delimitando los valores de corrosión posibles de analizar e indicando que a partir de un cierto nivel la falla puede ocurrir no por inestabilidades en la estructura, sino por una alta tasa de degradación del hormigón en la sección transversal.
Como lo observaron Pereira Junior et al. (2016), el daño se manifestó intensamente en las regiones traccionadas de la estructura y, la medida que aumentaba la fisuración, el encuentro de microfisuras condujo al proceso de fractura del material.
El hormigón alrededor de las barras de acero afectadas por la corrosión sufrió el desarrollo de fisuras, con un aumento gradual de la degradación conforme aumentaba el porcentaje de corrosión. Finalmente, la conexión de fisuras desarrolladas alrededor de las barras aumentó los efectos de segundo orden en la estructura.
4. Conclusiones
La corrosión, además de la degradación del acero, desencadena un proceso de deterioro del hormigón, comprometiendo el desempeño de la estructura frente a acciones externas y reduciendo su vida útil, ya que interfiere en su integridad, dejándola aún más susceptible al desarrollo de nuevas manifestaciones patológicas.
Este trabajo reprodujo una metodología para la simulación y validación del comportamiento mecánico de elementos estructurales en hormigón armado, sumando a esto el efecto mecánico impuesto por la corrosión, es decir, la intensificación del proceso de fisuración resultante del producto expansivo generado.
Con el presente estudio, se pudo definir que la corrosión influye negativamente en la estabilidad de los elementos en hormigón armado, ya que intensifica los esfuerzos globales de 2º orden en la estructura. Al comparar los valores del coeficiente γ z obtenidos con las simulaciones después de la adición de la corrosión con los calculados a partir de la NBR 6118: 2014, fue posible definir que los métodos presentes en la norma para la consideración de no linealidades físicas en el diseño, a través de modelos simplificados, son seguros para los niveles de corrosión analizados.
Sin embargo, los modelos también indicaron que a partir de un cierto nivel de corrosión, la falla estructural asociada con la degradación del hormigón, debido al desarrollo de fisuras, puede causar la pérdida del equilibrio interno en la sección transversal, es decir, incluso antes de que el aumento en los esfuerzos de 2º orden sea crítico.
Además, la reducción de la rigidez propuesta por la norma brasileña también debe considerar el efecto reológico del hormigón armado, de modo que la presencia conjunta de estos efectos y la corrosión puedan llevar la estructura a un estado no previsto por los modelos de cálculo simplificados. De esta forma, se recomienda que futuras investigaciones analicen los efectos reológicos en presencia de niveles intensos de degradación, con el fin de precisar el nivel de seguridad proporcionado por las simplificaciones normativas en este escenario.
References
Aitsin, A. C. et al. (2008), Constitutive modelling of high strength/high performance concrete. Internation Federation for Structural Concrete (FIB). Lausanne, Switzerland, p. 125. [ Links ]
Álvares, M. S. (1993), “Estudo de um modelo de dano para o concreto: formulação, identificação paramétrica e aplicação com o emprego do método dos elementos finitos”, Dissertação (Título de Mestre em Engenharia de Estruturas), Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, p. 123. [ Links ]
Amorim Júnior, N. S. A. et al. (2021), Durability and service life analysis of metakaolin-based geopolymer concretes with respect to chloride penetration using chloride migration test and corrosion potential. Construction and Building Materials, 287, 122970. https://doi.org/10.1016/j.conbuildmat.2021.122970 [ Links ]
Araujo, A. D. et al. (2020), Current condition of the exposed concrete façades reinforcement of the Vilanova Artigas building: modern architectural heritage. Revista IBRACON de Estruturas e Materiais, 14. https://doi.org/10.1590/S1983-41952021000100013 [ Links ]
Associação Brasileira de Normas Técnicas. (1988). NBR 6123: Forças devidas ao vento em edificações. Rio de Janeiro. [ Links ]
Associação Brasileira de Normas Técnicas. (2014). NBR 6118: Projeto de estruturas de concreto - Procedimentos. Rio de Janeiro. [ Links ]
Associação Brasileira de Normas Técnicas. (2019). NBR 6120: Ações para o cálculo de estruturas de edificações. Rio de Janeiro [ Links ]
Ayinde, O. O. et al. (2017), Numerical simulation of concrete degradation due to chloride-induced reinforcement corrosion. Proceedings of the 3rd international forum on energy, environment science and materials, v. 120. [ Links ]
Balestra, C. E. T. et al. (2018), Effect of corrosion degree on mechanical properties of reinforcements buried for 60 years. Revista IBRACON de Estruturas e Materiais, 11, 474-498. https://doi.org/10.1590/S1983-41952018000300003 [ Links ]
Blanco, Y. D. et al. (2019), Natural additive (nopal mucilage) on the electrochemical properties of concrete reinforcing steel. Revista ALCONPAT, 9(3), 260-276. https://doi.org/10.21041/ra.v9i3.429 [ Links ]
Branson, D. E. (1968), Procedures for computing deflections. ACI Journal, New York, n. 65. [ Links ]
Dietrich, Y. P. et al. (2017), Desempenho mecânico e análise da corrosão das armaduras em concretos produzidos com adição de resíduos de rochas ornamentais. Matéria (Rio de Janeiro), 22. https://doi.org/10.1590/S1517-707620170004.0225 [ Links ]
El-Maaddawy, T., Soudki, K. (2007), A model for prediction of time from corrosion initiation to corrosion cracking. Cement & Concrete Composites, v. 29, p. 168-175. https://doi.org/10.1016/j.cemconcomp.2006.11.004 [ Links ]
Favretto, F. et al. (2021), Modelos de estimativa do grau de saturação do concreto a partir das variáveis ambientais aplicados à análise de confiabilidade de estruturas de concreto armado atacadas por íons cloreto. Revista Matéria. 2021, 26(3): e13001. https://doi.org/10.1590/S1517-707620210003.13001 [ Links ]
Fédération Internationale du Béton/International Federation for Structural Concrete. (2010). CEB-FIB MODEL CODE. [ Links ]
Felix, E. F. et al. (2020), Development and analysis of a numerical model of the reinforced concrete expansion due to uniform corrosion. Revista de la Asociación Latinoamericana de Control de Calidad, Patología y Recuperación de la Construcción, 10(3), 300-316. https://doi.org/10.21041/ra.v10i3.395 [ Links ]
Felix, E. F., Carrazedo, R. (2021), Análise probabilística da vida útil de lajes de concreto armado sujeitas à corrosão por carbonatação via simulação de Monte Carlo. Matéria (Rio de Janeiro), v. 26. https://doi.org/10.1590/S1517-707620210003.13043 [ Links ]
Figueiredo, C. P. et al. (2014), O papel do metacaulim na proteção dos concretos contra a ação deletéria de cloretos. Revista IBRACON de Estruturas e Materiais, 7, 685-708. https://doi.org/10.1590/S1983-41952014000400008 [ Links ]
Franco, M., Vasconcelos, A. C. (1991). Practical assessment of second order effects in tall buildings. Colloquium on the CEB-FIB MC 90, COPPE/UFRJ, Rio de Janeiro, RJ. [ Links ]
Fusco, P. B. (2008), “Tecnologia do concreto estrutural: tópicos aplicados”. São Paulo: PINI. [ Links ]
Helene, P. R. L. (1993), “Contribuição ao estudo da corrosão em armaduras de concreto armado”, Tese (Livre-docência junto ao Departamento de Engenharia de Construção civil). Escola Politécnica, Universidade de São Paulo, São Paulo, p. 231. [ Links ]
Hibbitt, H. et al. (2011), Abaqus analysis user’s manual version, 6.10. Dassault Systèmes Simulia Corp.: providence, RI, USA. [ Links ]
Lee, J., Fenves, G. L. (1998), A plastic-damage model for cyclic loading of concrete structures. Journal of Engineering Mechanics, ASCE, v. 124, p. 892- 900. https://doi.org/10.1061/(ASCE)0733-9399(1998)124:8(892) [ Links ]
Lubliner, J. et al. (1989), A plastic-damage model for concrete. International Journal of solids and Structures, v. 25, n. 3, p. 299-326. https://doi.org/10.1016/0020-7683(89)90050-4 [ Links ]
Mackechnie, J. R., Alexander, M. G. (2001), Repair principles for corrosion-damaged reinforced concrete structures. Research monograph, 5, 1-36. [ Links ]
Maldonado-Bandala, E. E. et al. (2018), Evaluation of pathological problems associated with carbonation and sulfates in a concrete tower with more than 50 years in service. Revista ALCONPAT, 8(1), 94-107. https://doi.org/10.21041/ra.v8i1.284 [ Links ]
Malheiro, R. M. D. C. et al. (2014), Influência da camada do revestimento de argamassa na penetração de cloretos em estruturas de concreto. Ambiente Construído, 14, 41-55. https://doi.org/10.1590/S1678-86212014000100005 [ Links ]
Meira, G. R., Ferreira, P. R. R. (2019), Revisão sobre ensaios acelerados para indução da corrosão desencadeada por cloretos em concreto armado. Ambiente Construído, 19, 223-248. https://doi.org/10.1590/s1678-86212019000400353 [ Links ]
Pereira Junior, W. M. et al. (2016), Análise numérica de vigas de concreto com fibras de aço utilizando mecânica do dano. Revista IBRACON de estruturas e materiais, v. 9, n. 2, p. 153-191. https://doi.org/10.1590/S1983-41952016000200002 [ Links ]
Ramos, É. S., Carrazedo, R. (2020), Cross-section modeling of the non-uniform corrosion due to chloride ingress using the positional finite element method. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42(10), 1-18. https://doi.org/10.1007/s40430-020-02627-5 [ Links ]
Ramos, É. S., Carrazedo, R. (2021), Numerical analysis of reinforced concrete beam subject to pitting corrosion. Ambiente Construído, 22, 201-222. https://doi.org/10.1590/s1678-86212022000100588 [ Links ]
Reginato, L. (2020), “Contribuição ao projeto de consolos de concreto com base em simulações numéricas”. Dissertação (Título de Mestre em Engenharia de Estruturas), Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, p. 184. [ Links ]
Santos, B. et al. (2020), Effect of the addition of metakaolin on the carbonation of Portland cement concretes. Revista IBRACON de Estruturas e Materiais, 13, 1-18. https://doi.org/10.1590/S1983-41952020000100002 [ Links ]
Schvartzman, M. M. A. M. et al. (2010), Avaliação da corrosão sob tensão em aço inoxidável AISI 321 em ambiente de reator nuclear. Matéria (Rio de Janeiro), 15, 40-49. https://doi.org/10.1590/S1517-70762010000100006 [ Links ]
Silva, S. H. et al. (2015), Analytic Hierarchy Process to choose the cement type to protect reinforced concrete to corrosion caused by chloride ions attack. Revista ALCONPAT, 5(3), 174-189.https://www.scielo.org.mx/scielo.php?pid=S2007-68352015000300174&script=sci_arttext&%20tlng=en [ Links ]
Silvestro, L. et al. (2020), Penetração de cloretos em concretos expostos em zona de atmosfera marinha por um período de 9 anos. Ambiente Construído, 21, 101-118. https://doi.org/10.1590/s1678-86212021000100496 [ Links ]
Souza, V. D. B., Leonel, E. D. (2021), Probabilistic chloride diffusion modelling in cracked concrete structures by transient BEM formulation. Revista IBRACON de Estruturas e Materiais, 15. https://doi.org/10.1590/S1983-41952022000400002 [ Links ]
Teixeira, F. R. et al. (2021), Avaliação de propriedades relacionadas à penetração de cloretos em concretos produzidos com substituição parcial de cimento por resíduo de beneficiamento de rochas ornamentais. Matéria (Rio de Janeiro), 26. https://doi.org/10.1590/S1517-707620210003.13029 [ Links ]
Trevisol, C. A. et al. (2017), Avaliação de inibidores de corrosão para estruturas de concreto armado. Matéria (Rio de Janeiro), 22. https://doi.org/10.1590/S1517-707620170004.0238 [ Links ]
Verçoza, E. J. (1991), “Patologia das edificações”. [S.I.]: Sagra. [ Links ]
Wahrhaftig, A. M. (2008), “Uma avaliação experimental e numérica do efeito da rigidez geométrica na resposta dinâmica de estruturas esbeltas sujeitas à excitação de vento”. Tese (Título de Doutor em Engenharia), Escola Politécnica, Universidade de São Paulo, São Paulo, p. 209. [ Links ]
Yu, T. et al. (2010), Finite element modeling of confined concrete-II: Plastic-damage model. Engineering Structures, v. 32, n. 3, p. 680-691. https://doi.org/10.1016/j.engstruct.2009.11.013 [ Links ]
Recibido: 01 de Marzo de 2022; Aprobado: 08 de Julio de 2022











 texto em
texto em 

















