Article

 

The Role of Supramolecular Intermediates in the Potential Energy Surface of the Diels-Alder Reaction

 

Karla Ramírez-Gualito,^1* Néstor López-Mora,¹ Hugo A. Jiménez-Vázquez,^2* Joaquín Tamariz,² and Gabriel Cuevas^1*

 

¹ Instituto de Química. Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 Coyoacán, México D.F., México. Tel.: 52 (55) 56224659. karamirezg@prodigy.net.mx, gecgb@unam.mx.

² Departamento de Química Orgánica. Escuela Nacional de Ciencias Biológicas. Instituto Politécnico Nacional, Prolongación Carpio y Plan de Ayala, 11340, Miguel Hidalgo México, D.F. México.

 

Received February 6, 2013.
Accepted May 6, 2013.

 

Abstract

The potential energy surface of four stereoselective Diels-Alder reactions was studied, namely: cyclopentadiene-maleic anhydride, furan-maleic anhydride, the dimerization of cyclopentadiene, and cyclopentadiene-cyclopropene. For completeness, we also studied the reaction between ethylene and 2-hydroxy-6-methyl-1,4-benzoquinone, a [5+2] cycloaddition reaction. For all cases at least a stationary state of supramolecular nature a van der Waals complex, was determined. These stationary states are complexes formed by the interaction between the reagents, minima located in the paths between the non-interacting molecules and the transition states. The existence of these complexes makes it necessary to reconsider the role of Secondary Orbital Interactions in the selectivity of these reactions. As it is the case with other complexes, the stability of these supramolecular intermediates depends on electrostatic phenomena such as dispersion forces. The observation of [5+2] intramolecular complexes in solution is important since up to now, this kind of van der Waals complexes had only been described in the gas phase.

Keywords: Diels-Alder reaction, Dispersion forces, van der Waals complex, Reaction mechanism, Interaction energies.

 

Resumen

La superficie de energía potencial de cuatro reacciones estereoselectivas Diels-Alder fue estudiada, específicamente: ciclopentadieno-anhídrido maleico, furano-anhídrido maleico, la dimerización del ciclopentadieno y ciclopentadieno-ciclopropeno. Para complementar, también se estudió la reacción entre etileno y 2-hidroxil-6-metil1, 4-benzoquinona, una reacción de cicloadición [5+2]. Para todos los casos, fue identificado al menos un estado estacionario, un complejo de van der Waals de naturaleza supramolecular. Estos estados estacionarios de mínima energía son complejos formados por la interacción entre los reactivos y se localizan como mínimos en la trayectoria de las moléculas no interaccionantes y los estados de transición. La existencia de estos complejos hace necesario reconsiderar el papel de las Interacciones de Orbitales Secundarios en la selectividad de estas reacciones. De la misma forma que ocurre con otros complejos, la estabilidad de estos intermediarios supramoleculares depende de fenómenos electrostáticos como las fuerzas de dispersión. La existencia del complejo intramolecular [5+2] en solución es importante, ya que hasta ahora los complejos del tipo van der Waals sólo han sido descritos en fase gaseosa.

Palabras clave: Reacción de Diels-Alder, Fuerzas de dispersión, Complejo de van der Waals, Mecanismo de reacción, Energías de interacción.

 

Introduction

The existence of secondary orbital interactions (SOI) in cycloaddition reactions has been a controversial topic. While some research groups have reported results that have been interpreted as decisive proof of the participation of SOI in the stabilization of the transition states leading to the endo adducts of Diels-Alder reaction [1-7] others consider that there is no clear evidence to support this hypothesis. As a consequence, the selectivity of these reactions has been justified with arguments such as the participation of inductive forces [8], charge transfer phenomena between diene and dienophile, and accumulation of unsaturations [9, 10]. However, none of these arguments have been convincing enough.

Woodward and Hoffmann [1, 11, 12] analyzed a series of reactions to demonstrate the existence of SOI as the origin of the stereoselectivity in the Diels-Alder reaction. Among these Diels-Alder reactions, our study uses three examples, with two additional reactions, one of which is supported by experimental data: (a) The reaction between cyclopentadiene (1) and maleic anhydride (2), where it is well known that the endo product is formed as the major product under kinetic conditions and that it can be isomerized at 220 °C to yield a 45:55 mixture of endo/exo stereoisomers [13-15]. (b) The reaction between furan (3) and maleic anhydride (2) that initially produces the endo adduct, the kinetic product, which is rapidly transformed into the exo thermodynamic product under the reaction conditions [16-18]. (c) The dimerization of cyclopentadiene (3), and we included an additional example, (d) the reaction between cyclopentadiene (3) and cyclopropene (4). In the last two reactions, the endo stereoisomer is produced exclusively (Scheme 1) [19].

If SOI are indeed responsible of the stereoselectivity of these reactions, it would be expected that they would impact the enthalpic term in ∆G^≠, as it occurs, for example, in the enthalpic anomeric effect [20], where the stabilizing hyper-conjugative interaction strongly affects this term. In order to investigate the role of the SOI in the observed selectivity, we have studied the potential energy surface in the reaction trajectory of the aforementioned reactive systems and the results are described herein.

 

Results and discussion

The analysis of the evolution of energy as the reaction progresses for each one of reactions 1-3 (Scheme 1, eqs. 1-3) [21], within the two possible stereoisomeric endo/exo approaches, led to the location of two stationary states corresponding to minima (without imaginary frequencies) between the non-interacting reagents (separated at infinite distance) and the transition state (Fig. 1). For reaction 4, only one stationary state of this type was determined. These states are fundamental for this work since they lead us to reanalyze the current scheme used to describe and understand concerted processes. Until now it has been tacitly assumed that reactants do not really interact until they somehow reach and ride the reaction coordinate. Reaction coordinates are drawn and activation and reaction energies are calculated in terms of the properties of the isolated reactants. Reactivity schemes such as FMO theory are employed to predict selectivity in terms of the shape and energy of the orbitals of the isolated reactants at their unperturbed equilibrium geometries. In the more general scheme supported by this work, the isolated reagents interact first to produce an intermediate, a supramolecular complex that behaves as a unit, containing a new single set of molecular orbitals which results from the perturbation effect of each reactant on the other. These supramolecular stationary states are minima with substantial stabilization energies with respect to the isolated reagents. The relevance of the existence of these complexes is based in the fact that those complexes overcome to the solvent interactions with theirselves, exist when the reactants are located with a definite distance and orientation that becomes the origin of the endo and exo stereoselectivity. From the point of view of potential energy surface topology, these intermediates naturally make the associated transition states maxima in the reaction path; in other words, a saddle point isolated by two minima (an elemental reaction) just as it has been described by Suárez and Sordo [22]. These authors described for the first time the intermediacy of van der Waals complexes in the cycloaddition reaction between cyclopentadiene and maleic anhydride.

Several independent studies have reported stationary states similar to those described in Fig. 1; these include examples of 1,3-dipolar cycloaddition reactions [23-26] and the corresponding Lewis acid-catalyzed processes [27, 28]. However, these complexes have not been sufficiently analyzed in relation to their conceptual importance and it is not known whether they occur in isolated cases or if they are general to all Diels-Alder reactions, particularly when the diene and dienophile are electron-rich compounds.

Interestingly, when we studied the first reaction (Scheme 1, eq. 1) two orientations of cyclopentadiene (1) with respect to maleic anhydride (2) were found to correspond to minima, as described by Suárez and Sordo [22], those that formed the complexes that lead directly to the endo and exo transition states. The 5-endo and 5-exo stationary states (Scheme 2) calculated at the MP2/6-31G(d,p) level (method (a), (Fig. 1) were more stable than the compounds from which they were originated: the former by 7.19 and the latter by 6.18 kcal/mol, respectively. These same complexes calculated at the B3LYP/6-31G(d,p) level (method (b)) had a stabilization energy when compared to the reagents of -1.79 and -1.89 kcal/mol, and at the B3LYP/6311++G(2d,2p) level (method (c)) of 0.76 and 0.88 kcal/mol (Scheme 2). The interaction distance was also considerably different with the three methods used. With method (a), the distance between the atoms that will form the new carbon-carbon bonds when the reaction takes place was 3.103 Å for 5-endo and 3.338 Å for 5-exo. This is considerably shorter than the distance determined using methods (b) (resulting in 3.585 Å and 3.570 Å, respectively) and (c) (3.856 Å and 3.842 Å, respectively). On the other hand, the three methods predicted that the cyclopentadiene and maleic anhydride fragments remain essentially undistorted (flat) in the complex. This is in sharp contrast with the distortion of the reactants at the transition state, where the planarity is lost and both fragments are much closer.

These results are satisfactorily explained if one considers that the B3LYP method does not correctly describe dispersion forces, an issue that has been well documented [29, 30]; consequently, it fails to describe medium and long range interactions [31]. Interestingly, our results suggest that the description of the medium range interaction is worst when the largest basis set is used, a fact that is characteristic of DFT methods [32, 33]. On the other hand, when the transition state energy is calculated, it is well known that the B3LYP and MP2 methods tend to estimate it in opposite directions [34]. The B3LYP method usually underestimates barrier heights; however, this fact does not have an impact on the central topic of this work that focuses on the existence of the supramolecular intermediates shown in Fig. 1. Although it is expected that larger levels of theory would describe with more precision the reactions described in this work, both levels used here allowed confirming the existence of these intermediary complexes in the PES. It is important to point out that in this case, and in all the following cases, the PES of each system was studied in order to find other possible van der Waals π/π complexes, by rotating the diene in front of the dienophile and optimizing the rest of the variables, but only the minima herein described were found. The exclusive formation of the complexes with endo and exo orientation obeys the rules of conservation of orbital symmetry. This is important because there are no additional van der Waals complexes and the reaction trajectory must occur through the intermediates described herein. It is possible to find multiple CH/π stationary states, but these were not found to be such as intermediates in the cycloaddition process.

There are several reported cases which have shown that the inclusion of dispersion terms in the analysis of the molecular stability of complexes is essential in order to reproduce experimental results. Such are the cases of the benzene-hexafluorobenzene supramolecule [35], of the perezone conformers [36], and of the carbohydrate-protein interaction [37]. Since we obtained results analogous to those described so far for all the systems shown in Fig. 1, from here on, details will only be provided for the MP2 analysis of the remaining reactions.

To increase the precision in the evaluation of the interaction energy of these minima, the correction for BSSE was calculated using the counterpoise method proposed by Boys and Bernardi [38, 39-41]. The corrected interaction energy calculated for 5endo is -3.23 kcal/mol and for 5-exo is -2.78 kcal/mol. Thus, the difference in energy between the endo and exo complexes was only 0.45 kcal/mol. The incorporation of the BSSE correction during the geometry optimization of the supramolecular intermediates allowed us to find a stationary state with an associated imaginary frequency. This frequency describes the rotation of cyclopentadiene over maleic anhydride (or vice versa). The transition state thus found allows for the exchange between the endo and exo orientations of the supramolecule, and corresponds to an exchange path alternative to that found by Suárez and Sordo, which involves a third supramolecular intermediate and two additional transition states [22].

For an MP2 calculation, the total electronic energy is composed of two parts, the Hartree-Fock energy and the MP2 correction which corresponds to the correlation energy. Fig. 2 shows the curves obtained for each one of these terms as a function of the intermolecular distance for the endo and exo complexes. The corresponding values of ∆E_HF and ∆E_CORR, relative to the global minimum are presented in Table S3 in the Supporting Information.

In terms of the curves shown in Fig. 2, for the endo approximation the minimum in the potential energy curve for ∆E_CORR was located at a distance of 3.04 Å between the carbon atoms responsible for the interaction that produces the new C-C bond. For the exo approximation the minimum was found at a distance of 3.17 Å. In the case of the HF component, minima were not found until 5.0 Å for the the exo and 4.0 Å for the endo complexes. If the interaction had only an electrostatic origin, the HF results should have provided a proper description of the complex; in other words, they would be able to reproduce the depth of the minima at the intermolecular distance where the minima exist [35].

Therefore, the incorporation of the correlation energy, which includes the dispersion interaction between the cycloaddends, is a key factor to produce a well-determined minimum in the interaction energy curves, as observed in Fig. 2. On the other hand, the main contribution to the total energy of the complex comes from the HF term.

These results indeed establish the importance of considering the dispersion energy in the evaluation of the stability of the complexes involved in the Diels-Alder reaction. The dispersion energy is so important that even a small base such as 631G(d,p) is able to introduce a substantial part of the correlation correction. The endo complex is more stable than the exo, in agreement with the endo rule postulated by Alder for the corre-sponding transition states [42-45]. Dispersion energy would be largely responsible for this phenomenon, since the calculation at the MP2 level provides the minimum in the potential energy surface and includes the dispersion energy terms.

It can be concluded that the formation of these complexes has its origin mainly in the π/π interaction between the reactants, so it is controlled by dispersion forces which can only be represented appropriately by MP2 or higher levels of theory. The calculations with functionals that do not correctly describe long range interactions are useful here, since the comparison with the MP2 method allows us to verify that the interactions responsible for the formation of the complex require the correct description of long range terms (the dispersion forces).

The full profile of the reaction between cyclopentadiene (1) and maleic anhydride (2) is represented in Scheme 2. In addition to the higher stability of the 5-endo supramolecular complex, the endo transition state is more stable than the exo by 2.1 kcal/mol in agreement with previous results of Arrieta and Cossio [46] and other research groups, leading to a higher endo selectivity under conditions of kinetic control.

In the reaction between maleic anhydride (2) and furan (3) (eq. 2 in Scheme 1 and Scheme 3), it was possible to locate supramolecular complexes analogous to those already discussed, with the endo arrangement being more stable than the exo by 0.53 kcal/mol. The difference in the interaction energy calculated using the counterpoise method [38] between 6-endo and 6-exo was 0.56 kcal/mol in favor of the endo complex. These complexes are also more stable than the isolated cycloaddends and are minima in the potential energy surface.

Regarding the interaction distances in the 6-endo and 6exo complexes, the distance between the atoms that will form the C-C bonds of the final product was 3.107 Å and 3.145 Å, respectively. The decomposition of the total interaction energy in its HF and correlation terms allows us to study the effect of the correlation; hence, to establish the relevance of medium and long range electrostatic interactions in the stability and structure of the complexes. For the endo approximation, the minimum in the ∆E_CORR potential energy curve was located at 3.133 Å between the carbon atoms responsible of the primary interaction; for the exo approximation the distance was 3.145 Å. In the case of the ∆E_HF component, the minima never occurred until an intermolecular distance of 5.0 Å for the endo and exo approximations. Again, if the interaction had only an electrostatic origin, the HF results should have provided a proper description of the complex; however this was not the case.

The third case was the cyclopentadiene (1) dimerization. The difference in energy between the 7-endo and the 7-exo complexes was minimal (0.05 kcal/mol, Scheme 4). Both complexes were minima in the potential energy surface and the distances between the cycloaddends of the complexes are 3.330 Å and 3.410 Å for the endo approach, and 3.372 Å and 3.420 Å for the exo.

In this case the Hartree-Fock energy (∆E_HF) and the electronic correlation energy (∆E_CORR) as a function of the intermolecular distance are presented in Fig. 3 (See Table S9 of the Supporting Information). This figure shows that the MP2 term is the responsible of the existence of the minima that are produced at carbon atom distances of 3.5 Å for the endo intermediate, and 3.3 Å for the exo. However, it must be noticed that the HF term provides the main contribution to the stability of the exo complex that shows a minimum at 3.7 Å. No minima were found for the endo complex until 3.9 Å. This is in sharp contrast with the previous cases where the energetic difference is ∆E_CORR(endo) ≈∆E_CORR(exo) while for this case ∆E_HF(endo) > ∆E_HF(exo).

For the reaction between cyclopentadiene (1) and cyclopropene (4) (Scheme 5), the behavior of the endo/exo supramolecular complexes was different with respect to the previous reactions. While the π/π interaction was responsible for the formation of the 8-endo complex, the 8-exo complex did not correspond to a minimum. Several attempts to locate a minimum related to the exo approach between the reactants led to different minima, stabilized by CH/π interactions, which could not evolve directly into the exo cycloaddition product. Hence, it can be proposed that the origin of the observed endo selectivity would depend on the nonexistence of the exo complex. This fact is in agreement with experimental data, because the exo adduct has never been observed; nevertheless it is also possible to argue that the endo selectivity originates in the energy difference between the endo and exo transition states, 4.7 kcal/mol favoring the endo geometry. This value is more than enough to yield exclusively the endo product under kinetic conditions.

For this system, the distance between the atoms that will form the C-C bonds was 3.227 Å for the 8-endo complex at the MP2/6-31G(d,p) level of theory. At the B3LYP/6-31G(d,p) level, the distance was 4.830 Å; this confirms, once again, the importance of the correct description of medium and long range terms in order to study this problem and thus, the magnitude of the dispersion forces involved.

Now, a question arises: how general is the existence of this kind of complexes? The application of spectroscopic techniques such as Raman, microwave and infrared has allowed the study of supramolecular complexes in gas phase such as those described here [47]. Specifically, the spectroscopic evidence for supramolecular intermediates in 1,3-dipolar cycloaddition reaction between ozone and ethylene, in gas phase, has been described [23]. However, the complexes have not been described in condensed phase, so their existence must be proved. In fact, the effect of the solvent that is so important in the Diels-Alder reaction [48], could play an important role in preventing their formation.

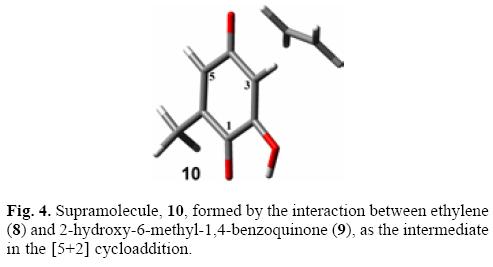
In order to address this issue we decided to study the [5+2] cycloaddition reaction between ethylene (8) and 2-hydroxy6-methyl-1,4-benzoquinone (9) (Scheme 6) [24-26], which is analogous to the intramolecular cycloaddition of perezone mentioned before [36]. The corresponding supramolecular complex (10) was a minimum in the potential energy surface and is shown in Fig. 4. The C3-C_ethylene distance was 3.541 Å, and C5-C_ethylene distance was 3.412 Å. The shorter distance for C5 can be attributed to the higher electrophilicity of this carbon atom due to the intramolecular hydrogen bond between the hydroxyl group at C-2 and the carbonyl group at C-1. The interaction energy of the complex was -2.56 kcal/mol at the MP2/6-31G(d,p) level.

For comparative purposes, the HF interaction energies calculated at the HF/6-31G(d,p)//MP2/6-31G(d,p) and the E_CORR energy at MP2/6-31G(d,p) level for the reaction between ethylene (8) and the quinone (9) are plotted in Fig. 5. The corresponding values ∆E_HF and ∆E_CORR are presented in Table S13 in the Supporting Information. As it was the case with the previous complexes, the correlation energy is responsible of the minimum observed at 3.54 Å between C3 and C_ethylene, while the HF component is unable to find a minimum until 4.5 Å. Again, for this molecular system the correlation energy contribution allows for the proper description of the minimum.

We have recently described the existence of stable intramolecular complexes that can be observed spectroscopically (NMR) [36] associated with the cycloaddition of perezone (Scheme 7), which are analogous to those described here [13, 49]. The existence of these complexes has undeniable chemical, electrochemical, and conformational consequences [36]. These are stationary states previous to the [5+2] cycloaddition reactions that yield the α- and β-pipitzols, and correspond to the intramolecular version of the complexes described in Fig. 4. The conformation of the perezone that approaches the alkylidene group to the quinone ring was deduced from the evaluation of the nuclear Overhauser effect that takes place between the methyl group of the quinone and the lateral chain. This establishes the formation of the complexes in the chloroform solution with a dielectric constant of 5.5 at 273 K and a dipolar moment of 1.02 D and thus, confirms the existence of supramolecular complexes in condensed phase. The polar solvent used was unable to impede forming the weak interactions that stabilize the complexes. It would be possible to suggest that entropy is responsible of the existence of these complexes. Although entropy-driven dissociation of these intramolecular complexes should be much less important than that of the intermolecular complexes and reactions considered in this paper. This is not the case, because the free rotation of the flexible lateral chain provides a large number of freedom degrees. Actually, the entropy drops drastically when the van der Waals complex and the pipitzol are formed. For the complex that leads to α-pipitzol, the distances between the atoms involved in the formation of the C-C bonds were 3.042 Å and 3.540 Å, while for the β-pipitzol were 2.972 Å and 4.190 Å, respectively. These distances are in good agreement with the analogous quinone system described above if one takes into account the differences between an inter- and an intramolecular cycloaddition, the steric crowding and the geometric restrictions generated by the approximation of the alkyl tether that contains the double bond.

The study of the stationary states associated with the reactions described in Scheme 1 was carried out at the MP2/631G(d,p), B3LYP/6-31G(d,p), and B3LYP/6-311++G(2d,2p) levels of theory. All electronic energy values reported herein for stationary states include Zero Point Energy (ZPE) corrections. In turn, the zero-point energies have been corrected using vibrational scaling factors calculated using the procedure suggested by Alcolea-Palafox [50] because for B3LYP/6-311++G(2d,2p) the scaling factor is not available. The calculated values are 0.9365 for MP2/6-31G(d,p), 0.9608 for B3LYP/6-31G(d,p) and 0.9668 for B3LYP/6-311++G(2d,2p) levels of theory. These scaling factors are in good agreement with those previously reported: 0.934 ± 0.045 for MP2/6-31G(d,p) and 0.961 ± 0.045 for B3LYP/6-31G(d,p) levels of theory, values suggested by the National Institute of Standards and Technology (NIST) [51]. The transition states were optimized using the QST2 method that uses the quadratic synchronous-transit approach and a qua-si-Newton or eigenvector-following algorithm to complete the geometry optimization [21, 52]. Basis Set Superposition Error (BSSE) corrections were incorporated by means of Boys and Bernardi's procedure [38]. Partial geometry optimizations were performed by fixing the C-C bond distances associated with the so-called primary interaction (see Supporting Information for distance values) and optimizing all the other variables with no symmetry constraints. These calculations were performed using Gaussian 03 [53]. It is well known that the MP2 method is better to describe medium and long distance interactions, which are relevant for the purpose of this paper that is only to describe the existence and the consequences of this kind of complexes.

 

Conclusions

The supramolecular complexes described in this work allow us to describe the reaction coordinates of Diels-Alder reactions in a more complete and logical way. The complexes correspond to minima located within the reaction coordinate, before the transition state; thus, the latter can be seen as a maximum located between two minima. Their existence also explains the "negative" activation energies, calculated in terms of the isolated reactants, in some reactions such as the cycloaddition of cyclopentadiene (1) and maleic anhydride (2) endo path, Scheme 2). The stabilization energies of these complexes relative to the isolated reactants can be substantial; for example, according to our results, in the cycloadditions of cyclopentadiene (1) or furan (3) with maleic anhydride (2) it is larger than 6 kcal/mol. The geometry of the complexes at the beginning of the reaction coordinate already describes the geometry of the approach. Even though according to the Curtin-Hammett principle, the energetics of the stereoisomeric (endo/exo) supramolecular complexes should not determine the selectivity of these reactions, the most interesting aspect of these van der Waals intermediates is that their relative stability seems to reflect already the relative stability of the corresponding transition states. Thus, it is likely that the structural factors that stabilize one supramolecular complex over the other are very similar to those that determine the relative stability at the transition state stage of the reaction coordinates, and hence the selectivity under conditions of kinetic control.

We also found that at the transition state level our results are similar to those reported previously by other works [2-7, 22, 46, 54]. In particular, the stationary points we located in the potential energy surface for the cycloaddition of cyclopentadiene (1) with maleic anhydride (2) are essentially the same as those described by Suárez and Sordo [22]. Our results also show that explicit electron correlation is very important in the description of supramolecular complexes, because dispersion forces play a substantial role in the complexation energy. As a consequence, DFT and HF methods do not describe correctly the interaction in these species.

The proposal of the existence of SOI implies that the reagents maintain their individual properties up to the transition state. However, when a previous minimum exists, the set of molecular orbitals of each reactant must combine with the set of the other to form a new and unique set of molecular orbitals for the complex. Thus, the individual molecules that constitute the complexes shown in Fig. 1 have lost their identities, so that it is not possible to discuss frontier orbitals for each fragment as there is a single HOMO and a single LUMO for each complex. However, the molecular orbital distribution of the complex is the result of the mutual perturbation of the molecular orbital sets of the reactants at the particular geometry of the minimum, and it should be analyzed and understood from this point of view. Therefore, it might be necessary to reconsider the generalization made by the Frontier Orbital Theory to account for the Diels-Alder reaction.

To the best of our knowledge, there are no reports of the experimental observation of the stationary states described in Fig. 1 in condensed phase (in this case in solution). However, the existence of the perezone conformers [36], in the intramolecular version of the [5+2] cycloaddition reaction discussed before (Scheme 7), opens a door to the study of these intermediates. The results presented here also show that as double bonds accumulate, the π/π interaction is strengthened because the stabilizing contribution of the dispersion energy interaction also increases [8]. Therefore, the origin of the endo rule of Alder can be found, at least in part, in these forces [42-45]. This means that the origin of any supramolecular complex does not depend solely on secondary orbital interactions, but that electrostatic forces such as dispersion play a fundamental role in their stabilization, and their existence overcome to the solvent interactions at a definite distance and orientation that becomes the origin of the endo and exo stereoselectivity.

 

Acknowledgement

KRG, NLM thank the Consejo Nacional de Ciencia y Tecnología (CONACYT) for scholarships. This work was supported by CONACYT through grant 49921-Q, and by DGAPA-UNAM grant IN-203510. We also thank the Coordinación de Comunicación y Sistemas de la Universidad La Salle, and DGSCA-UNAM for computer support. JT y HAJV are fellows of the COFAA-IPN and EDI-IPN programs. Supporting Information available from the authors: Full optimized geometries of the supramolecular complexes and the intermolecular distance effect in the interaction energy are included, and full reference 26.

 

References

1. Hoffmann, R.; Woodward, R. B. J. Am. Chem. Soc. 1965, 87, 4388.         [ Links ]

2. Stephenson, L. M.; Smith, D. E.; Current, S. P. J. Org. Chem. 1982, 47, 4170.         [ Links ]

3. Guner, O. F.; Ottenbrite, R. M.; Shillady, D. D.; Alston, P. V. J. Org. Chem. 1988, 53, 5348.         [ Links ]

4. Singleton, D. A. J. Am. Chem. Soc. 1992, 114, 6563.         [ Links ]

5. Loncharich, R. J.; Brown, F. K.; Houk, K. N. J. Org. Chem. 1989, 54, 1129.         [ Links ]

6. Caramella, P.; Quadrelli, P.; Toma, L. J. Am. Chem. Soc. 2002, 124, 1130.         [ Links ]

7. Wannere, C. S.; Paul, A.; Herges, R.; Houk, K. N.; Schaefer III, H. F.; Schleyer, P. v. R. J. Comput. Chem. 2007, 28, 344.         [ Links ]

8. Cioslowski, J.; Sauer, J.; Hetzenegger, J.; Karcher, T.; Hierstetter, J. Am. Chem. Soc. 1993, 115, 1353.         [ Links ]

9. Garcia, J. I.; Mayoral, J. A.; Salvatella, L. Acc. Chem. Res 2000, 33, 658.         [ Links ]

10. Herrera, R.; Nagarajan, A.; Morales, M. A.; Mendez, F.; Jimenez-Vazquez, H. A.; Zepeda, L. G.; Tamariz, J. J. Org. Chem. 2001, 66, 1252.         [ Links ]

11. Hoffmann, R.; Woodward, R. B. J. Am. Chem. Soc. 1965, 87, 2046.         [ Links ]

12. Woodward, R. B.; Hoffmann, R. Conservation of Orbital Symmetry; VCH: New York, 1970.         [ Links ]

13. Craig, D. J. Am. Chem. Soc. 1951, 73, 4889.         [ Links ]

14. Castner, K. F.; Calderon, N. J. Mol. Catal. 1982, 15, 47.         [ Links ]

15. Tlenkopatchev, M.; Vargas, J.; Almaraz-Girón, M. A.; López-González, M.; Riande, E. Macromolecules 2005, 38, 2696.         [ Links ]

16. Woodward, R. B.; Baer, H. J. Am. Chem. Soc. 1948, 70, 1161.         [ Links ]

17. Anet, F. A. L. Tetrahedron Lett. 1962, 3, 1219.         [ Links ]

18. Lee, M. W.; Herndon, W. C. J. Org. Chem. 1978, 43, 518.         [ Links ]

19. Binger, P.; Wedemann, P.; Goddard, R.; Brinker, U. H. J. Org. Chem. 1996, 61, 6462.         [ Links ]

20. Juaristi, E.; Cuevas, G. The Anomeric Effect.; CRC Press: Boca Raton, FL., 1994.         [ Links ]

21. Peng, C.; Schlegel, H. B. Israel J. Chem. 1993, 33, 449.         [ Links ]

22. Suárez, D.; Sordo, J. A. Chem. Commun. 1998, 385.         [ Links ]

23. Gillies, C. W.; Gillies, J. Z.; Suenram, R. D.; Lovas, F. J.; Kraka, E.; Cremer, D. J. Am. Chem. Soc. 1991, 113, 2412.         [ Links ]

24. Rivas-Islas, R., BSc Thesis, Universidad La Salle, 1999.         [ Links ]

25. Tovar-Velasco, E., MSc Thesis. Universidad Nacional Autónoma de México, 1998.         [ Links ]

26. López-Mora, N., MSc Thesis. Universidad Nacional Autónoma de México, 2005.         [ Links ]

27. Yamabe, S.; Dai, T.; Minato, T. J. Am. Chem. Soc. 1995, 117, 10994.         [ Links ]

28. Yamabe, S.; Minato, T. J. Org. Chem. 2000, 65, 1830.         [ Links ]

29. Zhao, Y.; Truhlar, D. G. J. Phys. Chem. A 2004, 108, 6908.         [ Links ]

30. Hyla-Kryspin, I.; Haufe, G.; Grimme, S. Chem. Eur. J. 2004, 10, 3411.         [ Links ]

31. Ruiz, E.; Salahub, D. R.; Vela, A. J. Am. Chem. Soc. 1995, 117, 1141.         [ Links ]

32. Lynch, B. J.; Zhao, Y.; Truhlar, D. G. J. Phys. Chem. A 2003, 107, 1384.         [ Links ]

33. Boese, A. D.; Martin, J. M. L.; Handy, N. L. J. Chem. Phys. 2003, 119, 3005.         [ Links ]

34. Zhao, Y.; Truhlar, D. G. Acc. Chem. Res 2008, 41, 157.         [ Links ]

35. Hernández-Trujillo, J.; Colmenares, F.; Cuevas, G.; Costas, M. Chem. Phys. Lett. 1997, 265, 503.         [ Links ]

36. Roura-Pérez, G.; Quiroz, B.; Aguilar-Martinez, M.; Frontana, C.; Solano, A.; Gonzalez, I.; Bautista-Martínez, J. A.; Jiménez-Barbero, J.; Cuevas, G. J. Org. Chem. 2007, 72, 1883.         [ Links ]

37. Fernández-Alonso, M. C.; Cañada, F. J.; Jiménez-Barbero, J.; Cuevas, G. J. Am. Chem. Soc. 2005, 127, 7379.         [ Links ]

38. Boys, S. F.; Bernardi, F. Mol. Phys. 1970, 19, 553.         [ Links ]

39. Simon, S.; Duran, M.; Dannenberg, J. J. J. Chem. Phys. 1996, 105, 11024.         [ Links ]

40. Hunt, S. W.; Higgins, K. J.; Craddock, M. B.; Brauer, C. S.; Leopold, K. R. J. Am. Chem. Soc. 2003, 125, 13850.         [ Links ]

41. Li, R.-Y.; Li, Z.-R.; Wu, D.; Li, Y.; Chen, W.; Sun, C.-C. J. Chem. Phys. 2004, 121, 8775.         [ Links ]

42. Alder, K.; Stein, G. Justus Liebigs Ann. Chem. 1934, 514, 211.         [ Links ]

43. Alder, K.; Stein, G. Angew. Chem. 1937, 50, 510.         [ Links ]

44. Alder, K.; Schumacher, M. Liebigs Ann. Chem. 1951, 571, 87.         [ Links ]

45. Martin, J. G.; Hill, R. K. Chem. Rev. 1961, 61, 537.         [ Links ]

46. Arrieta, A.; Cossio, F. P.; Lecea, B. J. Org. Chem. 2001, 66, 6178.         [ Links ]

47. Leopold, K. R.; Fraser, G. T.; Novick, S. E.; Klemperer, W. Chem. Rev. 1994, 94, 1807.         [ Links ]

48. Reichardt, C. Solvent and Solvent Effects in Organic Chemistry; Wiley-VCH: Weinheim, Germany, 2003.         [ Links ]

49. Joseph-Nathan, P.; Mendoza, P.; García, E. Tetrahedron 1977, 33, 1573.         [ Links ]

50. Alcolea-Palafox, M. Int. J. Quantum Chem. 2000, 77, 661.         [ Links ]

51. http://cccbdb.nist.gov/vibscalejust.asp.

52. Peng, C.; Ayala, P. Y.; Schlegel, H. B.; Frisch, M. J. J. Comp. Chem. 1996, 17, 49.         [ Links ]

53. Frisch, M. J. e. a., Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004.         [ Links ]

54. Houk, K. N. Tetrahedron Lett 1970, 11, 2621.         [ Links ]