Research
Electronic excitation of atoms by positron impact using the scaling
born approach
a Assessoria e Orientação Estudantil - AOE,
Cep: 12222-000, no 2375, São José dos Campos, São Paulo,
Brasil.
Abstract
We consider the efficiency of the scaling Born positron (SBP) approach, in
calculating reliable integral cross sections (ICS) for positron impact
excitation of electronic states in atoms. We will demonstrate, using specific
examples as H, He, Hg, and Mg, that this relatively simple procedure can
generate quite accurate ICS when compared with more sophisticated methods. In
the absence of the experimental data, comparisons are made with analogous
electron scattering.
Keywords: Born; positron; scaling
PACS: 34.80.Dp
1. Introduction
Similar to the electron, its anti-particle (positron) also has important scientific
and technological applications in a large variety of fields. A thorough presentation
of the many applications of positrons can be found, for instance, in the book by
Charlton and Humberston [1]. This includes
astrophysics, solar physics, bio-medicine (both diagnostics and therapy) and
materials science (defect studies and crystallography). From a more fundamental
perspective, positrons are essential in the formation of antihydrogen, understanding
elementary particle and positronium (Ps) physics, as well as in the investigation of
positron binding to ordinary matter, i.e. neutral atoms [1]. Resonances in electron-impact on atoms and
molecules are well-known; however, the situation with respect to positrons is not as
clear [1]. Positron binding energies have been measured for a large variety of small
targets [1], although only a few calculations
are available[1]. Positron scattering in the
gases phase constitutes a sensitive test for atomic interactions. The static
potential between the incoming electron and the fixed charge distribution in an atom
is attractive. Positrons inside an atom experience a repulsive static interaction
from the positive nucleus only partially screened by electrons. The opposite sign of
the static interaction for positrons cause a kind of compensation between the two
parts of the potential (static + polarization) and small adjustments of these parts
cause big differences in cross sections. New scattering measurements are very
important for comparison, setting new standards for both theoreticians and
experimentalists [1,2]. Indeed one rationale
for the present investigation is to try and shed more light on this state of
affairs. In the last few years, there have been several theoretical activities
concerning the positron-atom scattering at several energies [3]. Most of the work produced was based on ab initio methods
[3] and also classical collision theory
[3]. However, each of these models works
only on a limited range of targets and these calculations are very time consuming,
limiting the domain of applicability of such models.
In the present work we present a study on the simple scaling of plane wave Born cross
section which was created for positron-impact excitations of targets in general
[4]. The study is based on the traditional
first Born approximation (FBA). The FBA still is used as the starting point in
several studies, because (a) the plane wave is the correct wave function at infinity
for an positron colliding with a target, and (b) it is the simplest collision theory
that uses target wave function explicitly. Validating a scaling method for FBA cross
sections of atoms requires two initial ingredients: (i) the Born integral cross
sections themselves; (ii) reliable experimental or theoretical optical oscillator
strengths. The called BEf-scaling approach was found by Kim [5] to convert the FBA to reliable cross sections comparable to accurate
excitation cross sections at all incident electron energies above threshold. The BEf-scaling described by Kim [5]
correct the deficiencies of FBA into simple functional forms that depend on a few
atomic properties. Cross sections for positron and electron impact are virtually
identical at high energies and if the basic dynamical ingredients for this evidence
is the FBA, then it is possible extend the analysis developed by Kim [5] to more complicated systems, as
positron-atom scattering (this is a important consideration and can be significant
for studies using positron as incident particle) [4]. One of the complications created by the use of positron as incident
particle is the existence of additional positronium channels which are not present
in the case of electron scattering. Thus, we will present a study of the SBP
approach without Ps channel. The goal of the present scaling method is to provide a
simple theoretical method to calculate excitation cross sections comparable not only
to reliable experimental data, but also to more sophisticated theories. To our
knowledge, this study represents the first attempt to establish a theoretical
formulation for positron scattering using the called scaling Born positron (SBP),
i.e., a version for positron of originally BEf-scaling proposed by Kim [5] for
electron scattering.
In Sec. 2 we identify changes necessary to transform the model proposed by Kim [5] (electron scattering) and the present model
for positron scattering. In Sec. 3 we discuss the application of the method for
excitation of H, He, Hg, and Mg. Conclusions are presented in Sec. 4.
2. Theory
The scaling Born approximation described by Kim [5] for excitation of neutral atoms is applicable to dipole-allowed
excitations, and use atomic properties as excitation energy, ionization energy, and
the dipole f value that can be obtained, in principle, from accurate wave functions.
Since scaled cross sections are based on the plane wave Born approximation (FBA),
they do not account for the resonances often found near the excitation thresholds.
We will see that our method for positron scattering not only reduces the cross
sections magnitude at low energy, but also shifts the peak to a high energy than the
peak of the unscaled FBA, while keeping the high energy validity of the Born
approximation intact. In a generic form, first order Born cross sections σBorn(E) for inelastic collisions are written as [4,5]
σBorn(E0=4πERa02FBornE0
(1)
where ao is the Bohr radius, R is the Rydberg energy, Eo is the incident positron energy, and FBornE0 is the collision strength (multiplied by a constant to be consistent
with the standard definition of the collision strength). The SBP cross sections are
described as
σSBP={(faccur/fBorn)(E0/[(E0+Eps+Eexc)])}⋅σBorn
(2)
where E0 is the incident positron energy, faccur is an accurate dipole value from experiments or from accurate
wavefunctions, and fBorn is the dipole value from the same wavefunctions used to calculate the
unscaled Born cross section (σBorn), Eps is positronium energy, and Eexc excitation energy. The amplitude for the FBA is given by
fBorn=-(1/2π)∫d3rei(ki-kf)⋅r⟨Φf|V|Φi⟩
(3)
In Eq. (3), V is the positron-target interaction potential while Φi and Φf are initial and final electronic states of the target, respectively.
Scattering amplitude obtained from FBA are valid for high-energy static
calculations, i.e., situations where the target wave functions can
be considered frozen. For inelastic scattering, the FBA can be justified only by a
favorable comparison with more elaborate methods. As we will see, the SBP approach
represent a considerable improvement on the FBA, indicant cross sections with the
same order of magnitude as the more sophisticated calculations. The (Eps+Eexc) term used in Eq. (2) is a constant for each Z of the target and is related with the energy change of the incident
positron in the field of the nucleus and the bound electrons of the target. From
low-energy investigations, it is expected that a slow positron can distort
considerably the electronic cloud. A connection between this consideration and the
Eq. (2) may be related to the polarizability of the target. First, a hint to the
meaning of adding (Eps+Eexc) to E0 may be found in the FBA cross section for the elastic scattering from
the Yukawa potential. The Yukawa potential is a screened Coulomb potential,
v(r)=-(Z/r)exp(-r/β)
(4)
where r is the radial coordinate, Z is the atomic number and β is the “range” of interaction with dimension of length. Using plane
waves for the incident electron, the integrated cross section for elastic scattering
is
σBorn=16πZ2β4/[1+4k2β2]
(5)
where k is the momentum of the incident electron in atomic units. After writing β=ba0 and noting that (ka0)2=T/R, Eq. (4) becomes
σBorn=4πa02RZ2b2/[T+R/4b2],
(6)
which has the T in the denominator shifted by a Constant with the dimension of energy.
This analogy with the Eq. (2), suggests that the constant (Eps+Eexc) may be related to the shielding of the nuclear charge by the bound
electrons of the target (at higher energies the integral cross sections for elastic
and inelastic positron-target scattering are expected to be similar). Is relevant to
note that our cross sections using the SBP approach are consistent with
sophisticated methods and a particular interest, is to check if the SBP approach is
capable, for instance, of describing cross sections consistent with the literature
(without Ps channel).
3. Results and discussion
We present the calculated integral cross sections (ICS) for H, He, Be, Mg, and Hg
atoms by positron scattering and the cross sections are compared to other theories
and experiments (these atoms are chosen because recent experimental data for
electron scattering are described in the literature, and hence well suited as a
benchmark for our method using positron as incident particle). For all targets we
used the theoretical f deduced by Kim [5] and the wave
functions for the excited electronic states were all generated with the improved
virtual orbital [4].
H-atom
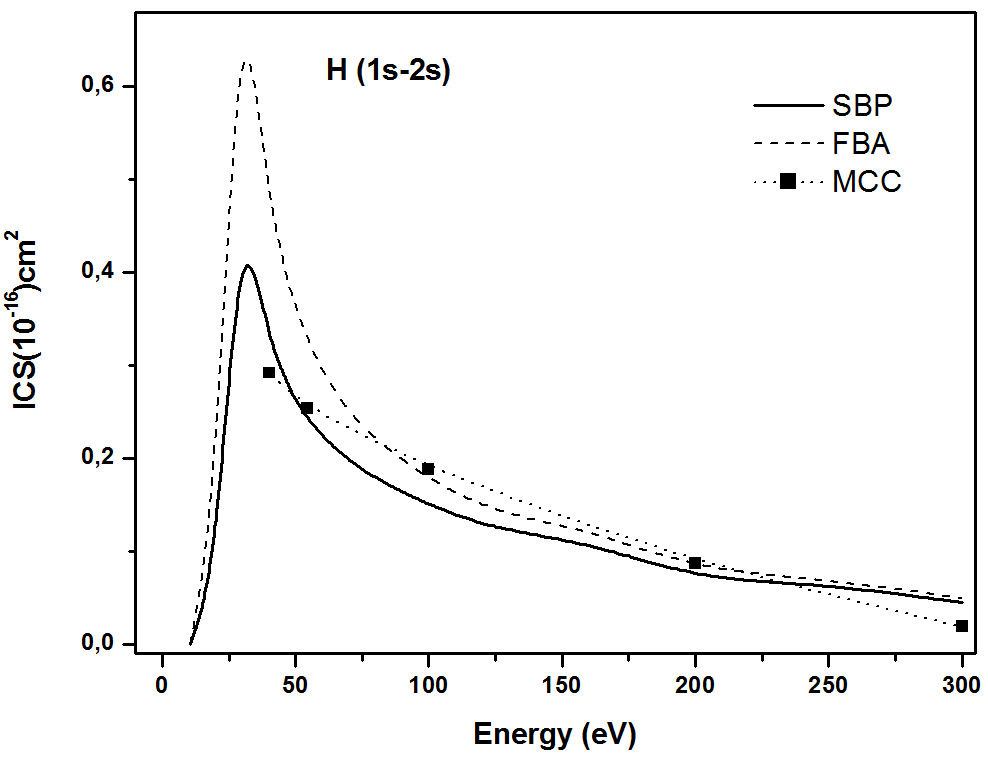
We performed calculations for the Hydrogen atom as our starting point and the ICS
for transition 1s-2s (Eexc=10.2eV, and Eps=6.8 eV) shown in Fig. 1. As
observed the FBA cross section for this electronic transition is large, and the
SBP cross section is very similar with the multi-state close coupling (MCC)
calculation of Walters [6]. We can note
also in Fig. 1 that the SBP approach not
only reduces the cross section magnitude at low energy, but also shifts the peak
to the high energy than the peak of the FBA, while keeping the high energy
validity of the FBA intact.
In Fig. 2, the integral cross sections (ICS)
using the SBP approach for the 1s-2p excitation of H atom are compared to the
MCC [6] method. Note in Fig. 2 a good level of agreement between the
SBP approach and the MCC method [6].
In the high energy region, the polarization interaction, changing with the impact
velocity, becomes relatively weaker. For the static potential, FBA predicts
equal cross sections for positron and electrons [3]. This convergence (cross sections) for positron and electrons
can be observed using Eq. (2), i.e,
σpositron≈σelectron≈σBorn
(7)
Figure 3 shows this effects on the
electronic excitation process of H atom. Cross sections for positron scattering
using the SBP approach (1s-2p, state) close with cross sections for electron
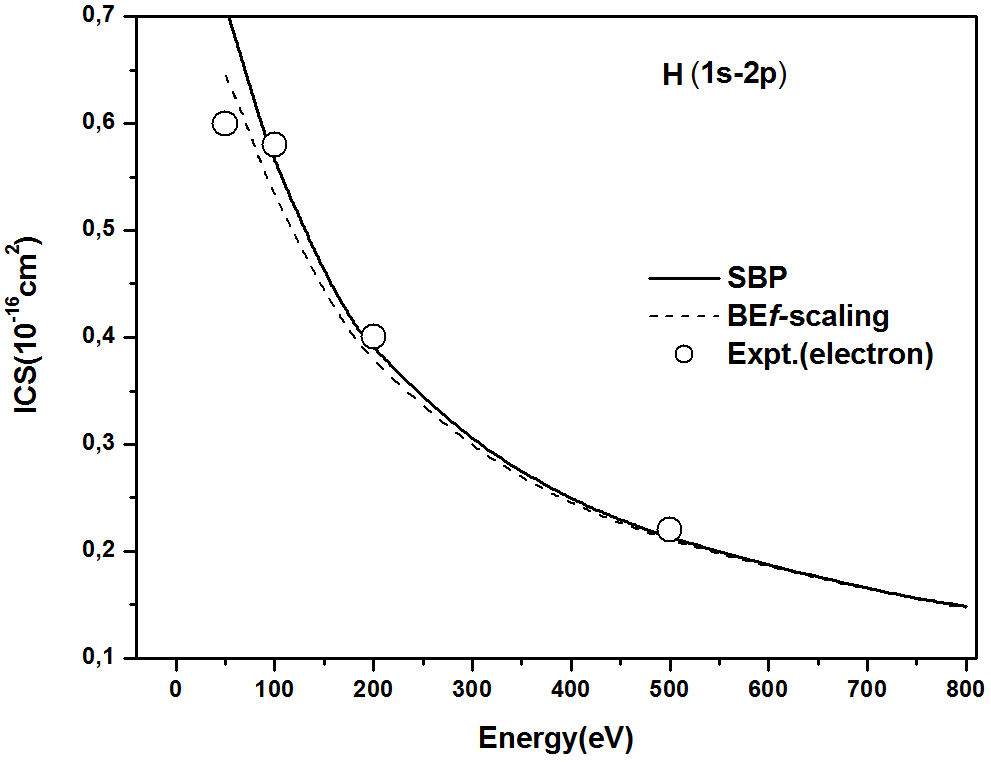
scattering at high energies, without losing its well-known validity at high E0, Eq. (4). As observed, the SBP approach is very similar with BEf-scaling [5] and as expected,
predicts equal cross sections for positrons and electrons.
He-atom
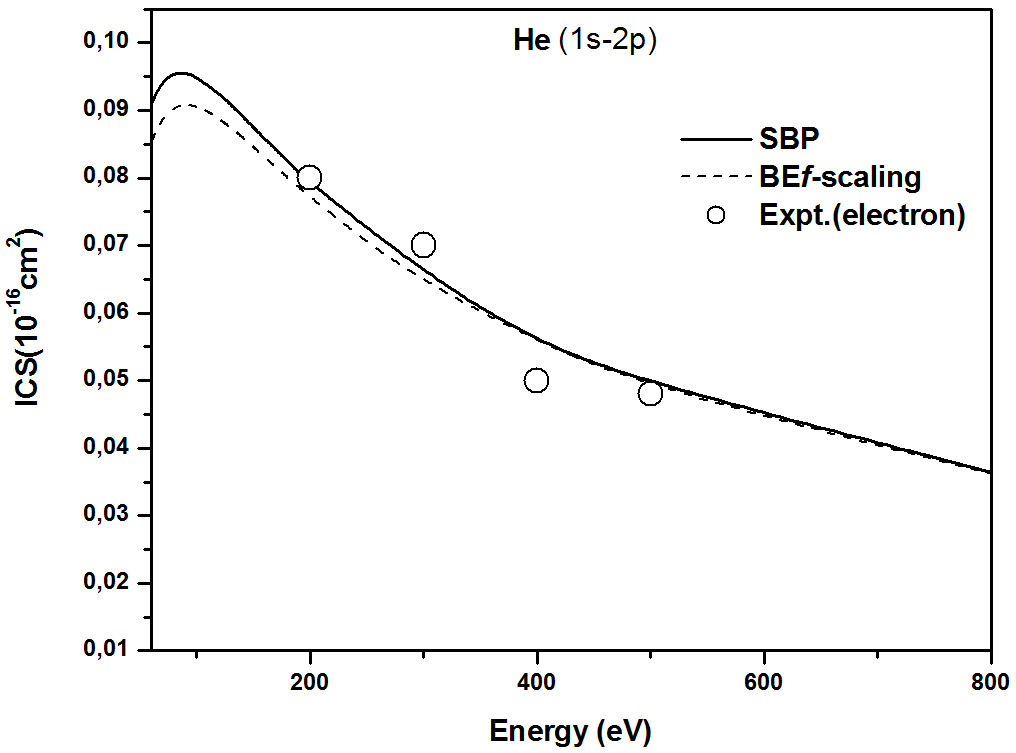
Figure 4 shows the integral cross sections
(ICS) for e+-He excitation (1s-2p), Eexc=21.21eV, and Eps=17.78 eV. As noted, the SBP approach is reasonably consistent with the
convergent close coupling method (CCC) [7] and experimental data [8].
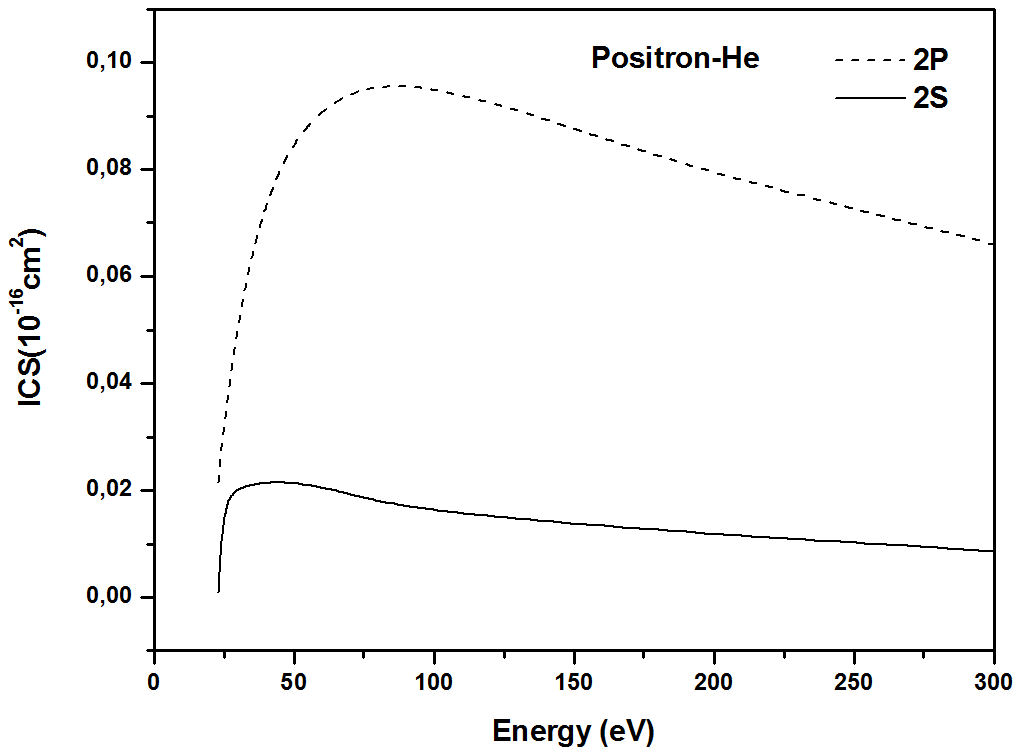
Figure 5 shows the relationship between the
states 21S, and 21P for He atom. Integral cross sections for positron excitation of the
He atom are compared. As expected the 21P state is dominant, and hence well suited as a benchmark using the
SBP model.
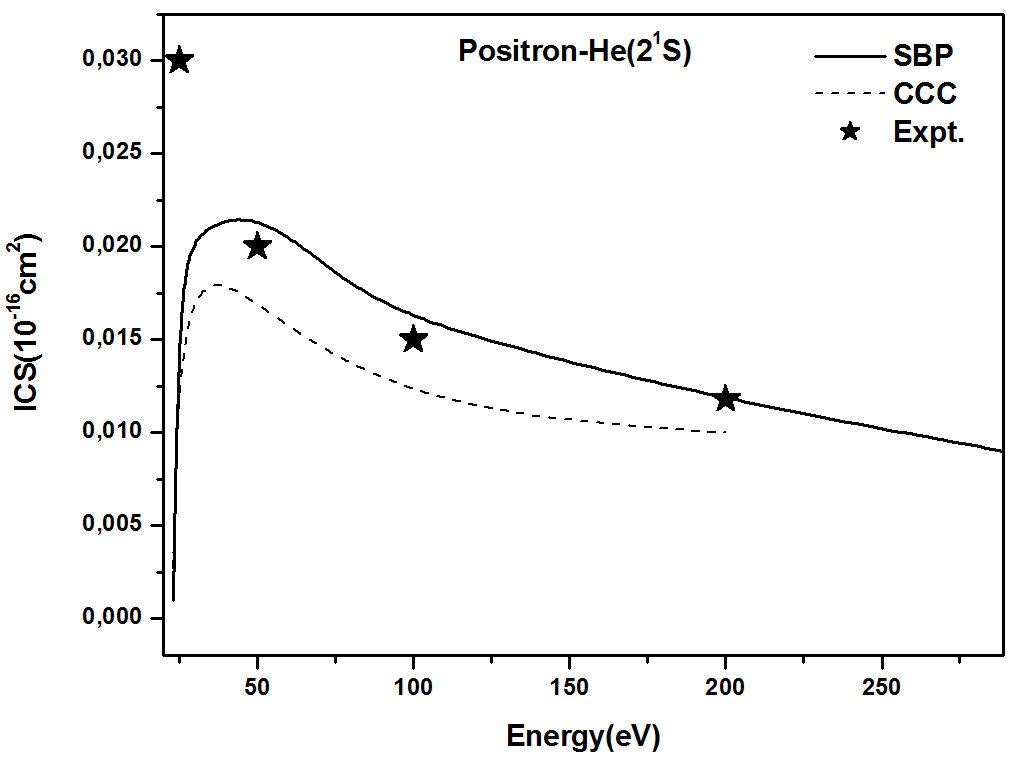
Figure 6 shows a similar agreement between
the SBP approach and the sophisticated CCC method [10] for the 21S state of He atom. Again the SBP model is consistent with
experi-mental data [8]. The performance
of the SBP approach for He atom is remarkable, particularly in view of the
simplicity of the scaling.
As in Fig. 3, the Fig. 7 shows the SBP approach compared with BEf-scaling for electron scattering. Note again the good agreement at
high energies. As expected, the SBP is applicable at high energies,
i.e., the cross sections suggests that the SBP approach
does offer a very useful alternative.
Be atom
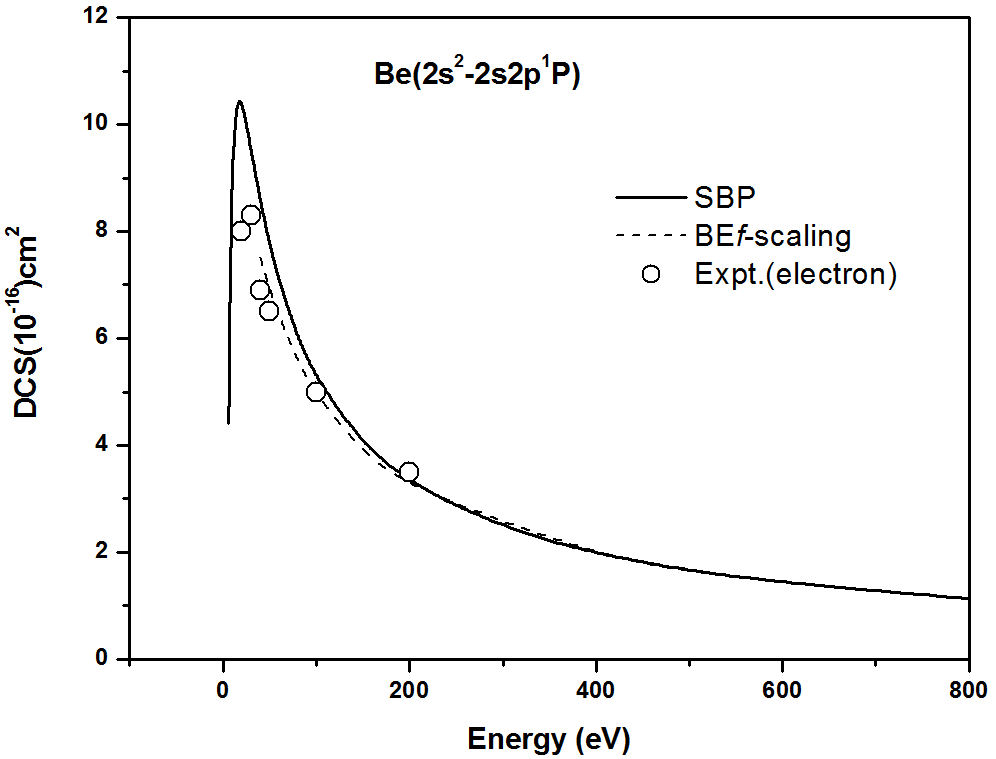
Figure 8 presents the SBP approach cross
sections for the Be atom (2s2-2s2p1P sate, Eexc=
5.27 eV, and Eps=2.52 eV). In the absence of experimental data and theoretical studies,
our results are compared with BEf-scaling (electron) and experimental data (electron) [5]. As noted the SBP again close with BEf-scaling for electron scattering at high energies.
Hg atom
Figure 9 shows the SBP approach cross
sections for the Hg atom (6s2-6s6p1P, Eexc=6.70 eV, and Eps=3.63 eV). In the absence of experimental data and theoretical studies ,
our results are compared with BEf-scaling (electron) and experimental data (electron). As noted the
SBP approach again close with BEf-scaling at high energies.
Mg atom
The Mg atom has a ground state Ps formation threshold of only 0.8 eV which is
closer to zero energy than any ground or excited state Ps formation thresholds
for the alkali atoms. In addition to this, Mg is a member of the alkaline earth
metals family of elements which has never been investigated in an e+ scattering experiment. As cited before in the SBP approach, the
Ps-channel is not considered but the Fig.
10 clearly demonstrates the utility of the present SBP approach, even
without Ps-channel the cross sections are consistent with the sophisticated
close coupling method (without Ps-channel)[9]. As observed again, the SBP approach does offer a very useful
alternative method.
4.Conclusions
A study of various transitions in positron scattering with ground-state of atoms has
been performed using the scaling Born positron (SBP) approach, without the
Ps-channel. The inelastic cross sections scattering are reported for low,
intermediate and high energies. We observe that the inelastic cross sections using
the SBP approach become relatively well converged with sophisticated methods. The
SBP approach is a simple representation of the Born cross sections and in this
sense, the present approach retains much of the utility of the original Born model
and requires a relatively small amount of computing effort. The SBP described here
will facilitate the calculation of integrated excitation cross sections for many
atoms, making the formulas ideally suited for molecules and other applications where
cross sections for a wide range of incident energies are required. The SBP approach
is relatively simple compared to state-of-the-art ab initio
theories.
References
1 M. Charlton, J.W. Humberston, Positron Physics
(Cambridge University Press, Cambridge, 2001).
[ Links ]
2 T.J. Murphy, C.M. Surko, Phys. Rev. A 46 5696
(1992);
[ Links ]
C.M. Surko , G.F. Gribakin, S.J. Buckman, J.Phys.
(2005) B38 R57.
[ Links ]
3 F. Salvat, Phys. Rev. A 68 (2003)
012708.
[ Links ]
4 J.L.S. Lino, Rev.Mex.Fis. 63 (2017) 303;
[ Links ]
J. L. S. Lino, Rev. Mex. Fis. 62 (2016) 596;
[ Links ]
J.L.S. Lino, Chin. J. Phys. 54 (2016)
223.
[ Links ]
5 Y.K. Kim, Phys. Rev. A . 64 (2001) 0327131;
[ Links ]
Y.K. Kim, Phys. Rev. A 65 (2002) 022705.
[ Links ]
6 H.R.J. Walters, Phys. Rep. 116
(1984).
[ Links ]
7 C.Y. Jun, Z.Y. Jun, Chin. J. Phys. 19 (2010)
063405.
[ Links ]
8 H. Wu , I. Bray, D.V. Fursa, A.T. Stelbovics, J. Phys.
B 37 (2004) 1165.
[ Links ]
9 See, T.S. Stein et al., Nucl. Instr.
Meth.Phys. Res.B 143 (1998) 68.
[ Links ]














 nova página do texto(beta)
nova página do texto(beta)