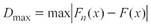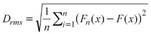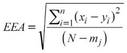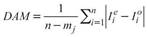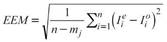Introduction

Precipitation as a hydrological state variable can be characterized by its intensity, distribution in space and time, and occurrence frequency or probability. In order to achieve this, numerous observations extracted from pluviographic series are necessary, defining the behavior pattern in a given area and allowing a later analysis or use. The most frequently used methodology is related to the Intensity-Duration-Frequency curves (IDF) that are used in hydrological engineering for the proposal, design, and operation of hydraulic projects, and engineering works for protection against maximum flash floods (^{Koutsoyiannis et al., 1998}).

In the early 1930s, ^{Sherman (1931)} and ^{Bernard (1932)} set out the first mathematical relationships. ^{Svensson et al. (2007)}, ^{Antigha and Ogarekpe (2013)}, and ^{Elsebaie (2012)} developed and specified mathematical expressions in Scotland, Nigeria, and Saudi Arabia, respectively. The results are graphically represented through maps of the rain intensity for different duration and return periods (^{Pereyra et al., 2004}). The IDF curves are also one of the most frequently used tools to estimate design storms in sites where there is not enough information about flow rates and discharge flows (^{Vélez et al., 2002}).

In order to develop the IDF curves, the maximum intensity values must be fitted to one FDP, which varies according to the zone modeled. In the Netherlands, ^{Overeem et al. (2008)} used the GEV function, because it has more conservative values for high return periods than the Gumbel distribution. In Saudi Arabia, ^{Al-Anazi and El-Sebaie (2013)} tested Gumbel, Log Pearson Type III,and Log Normal distributions, and they obtained good results in goodness-of-fit tests for all of them. ^{Svensson and Jones (2010)} studied the distribution functions used in the world and indicated that the most frequently used distribution function was the GEV. In Spain, the Gumbel function was frequently used until 20 years ago. Currently, the most recommended function used in official publications (^{Ministerio de Fomento, 1999}) is the SQRT-ET max distribution, known in Mexico as TERC (square-root exponential type). For maximum precipitations, ^{Salas and Fernández (2007)} recommend the use of TERC instead of Gumbel, GEV, Log Pearson Type III, and Two-component extreme value distribution (TCEV) (^{Rossi et al., 1984}).

In the case of the areas under study, the climatic conditions of the Segura River Basin which have very extensive and extremely low flow cause short-duration and high-intensity rains. Usually, these rains result in floods with overflows and maximum flows of the same nature as the greater known values in the world for basins with similar area (^{Pérez and Gil, 2012}, ^{Romero and Maurandi, 2000}). Therefore, in this type of semi-arid regions, establishing IDF relationships is necessary to define short-duration storms (less than 60 minutes) for proper hydrological and hydraulic planning and management, as well as for the correct sizing of infrastructures (^{Jiang and Tung, 2013}).

The objective of this study was to obtain the IDF curves for 15, 30, and 60 min intervals in the Segura River Basin, located in southeastern Spain, and to determine which of the FDPs studied fits better each one of the stations under consideration. In addition, the analytical expressions of the IDFs in the those stations will conform a source of information that will allow researchers to find out the intensity of rain required in any place of this basin, depending on the return period under consideration.

Materials and Methods

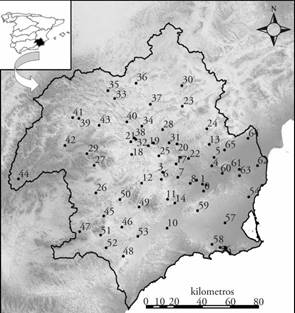
The Segura River Basin is located in the southeast of Spain (Figure 1) and it has an area of 18208 km². The height zoning results in the following distribution: 18 % of the area is located below 200 m altitude, 40 %, below 500 m, and 81 %, below 1000 m. Its streams transport small magnitude flows (65 Mm³ total) that are consumed locally, without providing significant returns to the Segura River. The meteorological station network managed by the organization of the Segura River Basin (Confederación Hidrográfica del Segura) is composed of 66 stations (Figure 1). The data provided by each pluviograph consist of rainfall records (every 5 min), from the hydrological 1992-1993 year to the 2012-2013 year. Of the 66 initial stations, stations number 2, 39, and 40 were discarded due to lack of records in several years. For each one of the remaining 63 stations, the maximum annual intensities were obtained in 15, 30 and 60 min intervals, since there are precedents of short rains of great intensity and high impact that caused serious material damages. All this has an impact on their relevance (^{Machado et al., 2011}; ^{Hooke and Mant, 2002}). These storms determine the sizing of rainwater harvesting systems and storm tanks; therefore, information about rainfall with specific duration and frequency is necessary (^{Jiang and Tung, 2013}).

Figure 1 Study area and meteorological stations location. 

In order to verify the independence and homogeneity of the recorded series, the Von Neumann test (^{WMO, 1971}) and the Wald-Wolfowitz test (^{Bobée and Ashkar, 1991}; ^{Rao and Hamed, 2000}) were applied. The calculation of the Neuman and Wald-Wolfowitz tests was carried out using the R Core Team climtrends and randtests packages (^{Mateus and Caeiro, 2014}). The mean value obtained with the Neumann test at the stations under study was above 2.1, for the storm durations under study, with a standard deviation of less than 0.45. Only station number 31 showed a value lower than the critical: 5 % of 1.30 for n=20 (^{Bartels, 1982}); therefore, we decided to discard it. Finally, after the Wald-Wolfowitz test was applied, stations 20 and 38 did not guarantee the independence of the series, leaving a total of 60 stations in which the study was carried out.

With the spatial distribution of the maximum intensities for 15, 30, and 60 min durations, an interpolation of mean values and typical deviations of the intensities was carried out for the durations in each station (Figure 2).

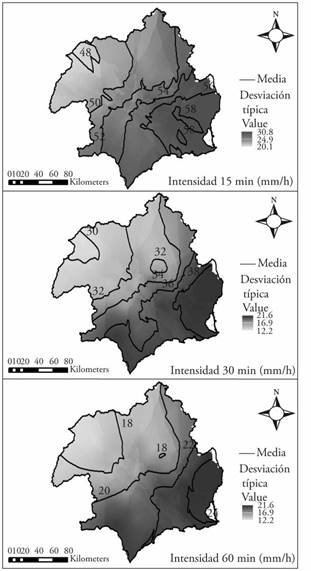
Figure 2 Spatial variation of the rain intensities statistics for 15, 30, and 60 min. in the Segura River Basin, Spain. 

The interpolation was carried out with Arcmap 10.2, using an ordinary kriging with a spherical semivariogram. The intensities and their variability increase from northwest to southeast (Figure 2). For 15 min periods, approximately 54 mm h^-1 mean intensities were recorded, versus 35 mm h^-1 and 20 mm h^-1 for 30 min and 60 min, respectively. The intensities’ standard deviations reach values higher than 30 mm h^-1 for 15 min periods which means maximum intensities close to 80 mm h^-1; however, if the time is extended to 30 or 60 min, these large deviations are reduced and stabilized at maximum values of 20 mm h^-1.

The FDPs used in this study were Gumbel, GEV, Log Pearson Type III (LPIII), and TERC (Table 1). All FDPs were adjusted using the method of moments (MO), except the GEV in which the L-moment (ML) method was used. The adjustments obtained in each station were evaluated using the D_max (1) and D_rms (2) versions of the Lilliefors test, (^{Hennemuth et al., 2013}) and the standard error adjustment (3) (EEA) (^{Kite, 1977}).

Table 1 FDP used in the study 

()1

()2

()3

where

F(x): theoretical value of the distribution function of extreme values;

F _n(x): value of the empirical probability distribution function (FDP);

x _i: past values of the sample;

y _i: values obtained with the FDP;

n: sample size; m _j:

number of parameters of the FDP.

Once the best adjusted function has been selected, the analytical expressions of the IDF curves are also obtained, using the ^{Aparicio (1997)} method, based on the following equation: I=K T ^m D ^-n (4), where T is the return period in years, D is the duration of the storm in minutes or hours, and I is the precipitation intensity in mm h^-1. If logarithms are extracted from each side of the equation, the result is a multiple linear regression model of the log I=log k+m log T-n log D (5) type, where k, m, and n are the constants to be adjusted for each station. In order to verify the goodness-of-fit of the Aparicio equation (1997) in the real domain (^{Pandey and Nguyen, 1999}), the mean absolute deviation (DAM) (6) and the standard error of the mean (EEM) (7) were used (^{Campos-Aranda, 2014}).

()6

()7

where :

i _i ^e : estimated intensity;

i _i ^o : observed intensity

Results and Discussion

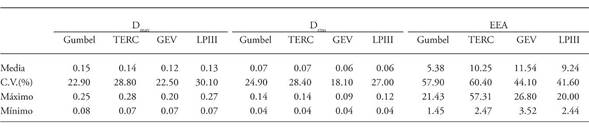
Out of 60 stations studied, 27 had the best adjustment with the Gumbel function representing 45 % of the basin, while the GEV and LPIII FDP were used in 19 and 12 stations, respectively. The TERC function only had the best adjustment in two stations. If the basic statistical parameters of the D _max, D _rms, and EEA values obtained for all stations are analyzed, the mean values for both D _max and D _rmsare very similar for all FDPs ranging from 0.15 to 0.13 for D _max, and 0.07 to 0.06 for D _rms. Therefore, taking into consideration only the Lilliefors test, any of the studied FDPs offers good adjustments for the Segura River Basin (Table 2). A similar behavior is observed in the coefficients of variation (CV), although they show a wider range and smaller oscillations, for the Gumbel and GEV functions.

Table 2 Basic statistics of FDP adjustments 

CV: Coefficient of Variation

However, the major differences between the FDPs appear in the EEA. The Gumbel function has an average EEA value of 50 % less than the other functions. The maximum value of the TERC function is three times higher than other functions. The Gumbel function presents the lowest values in the basin. GEV and LPIII have an approximately 40 % variability, while the CV increases up to 60 %, for the Gumbel and TERC functions.

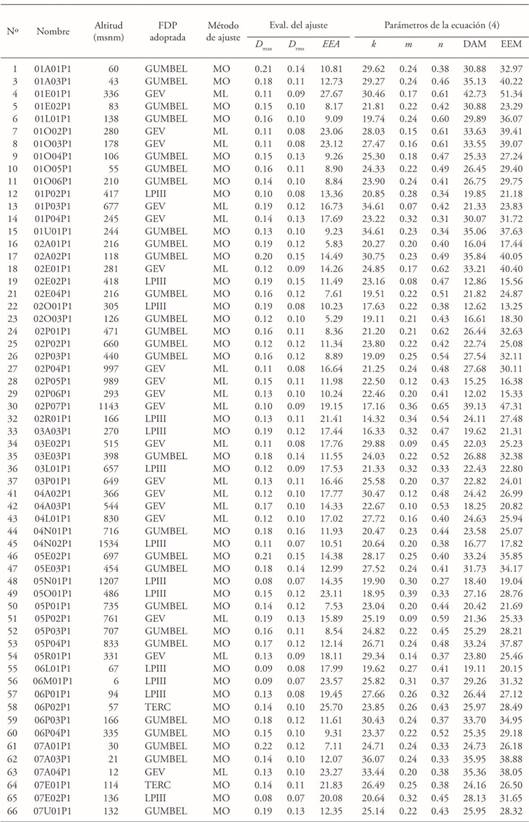
Table 3 includes a summary of the results obtained from the 60 stations analyzed. In addition to indicating which FDP fits better each one based on the results of the adjustment evaluation,the IDF equation (4) is set by means of the definition of the parameters on which k, m and, n depend.

Table 3 Summary of the results 

Taking into account the overall series, both DAM and EEM offer mean values around 25. with a 26 % and 28 % variability, respectively. If the goodness-of-fit is analyzed for 10+ years return periods, the values included in the table are reduced more than half in most of the cases ,because all the FDPs overestimate the intensities for less than 10 years return periods, but offer an optimal adjustment for 5-10+ return periods.

Once the parameters of each empirical equation were calculated for each one of the stations under consideration, the k, m, and n values of the equation (4) can be weighted for any locality in the Segura River Basin, Spain, based on the inverse square relationship, taking care to transport the information corresponding to the same altitudinal floor.

Conclusions

All the FDPs studied offered very similar values when the D _max and D _rms versions of the Lilliefors test were applied, requiring the calculation of the EEA, in order to effectively compare the FDPs and the selection of the best function for each one of the stations under consideration. The Gumbel function was better fitted to 45 % of the basin stations, the GEV in 32 %, the TERC only at two of the 60 stations. The widespread use of the TERC function in Spain requires a regionalized review and study, in order to justify or discard its use.

The analytical adjustment of the IDF curves using the linear regression method (^{Aparicio, 1997}) showed overestimations for return periods of less than 10 years. However, the deviations for higher return periods regularly used to size hydraulic infrastructures were significantly reduced. This validates the use of expressions calculated at any point of the basin, based on the inverse square relationship of the calculated values.