nova página do texto(beta)
Inglês (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
1 Introduction
Fractional order partial differential equations have been among the hot topics discussed recently in books [1,2] and many research papers [3-34]. Solitary wave solutions are considered a significant challenge in many disciplines, ranging from biology, quantum chemistry, electrodynamics, viscoelasticity, image processing, systems identification and optical fibers to fluid mechanics. Well known traditional approaches based on auxilary equations are known to have efficiencies for obtaining solitary wave solutions. Fractional order equations are currently used in several modern technologies of the twenty first century such as optical imaging, the study of waves on dam water, solid state physics and swinging in quantum mechanics. Since such equations contain a wide range of applications, it is important for researchers to construct and apply robust algorithms for the solutions of fractional equations. In many fields of science and engineering, especially in physical problems, several techniques have been proposed to obtain exact or approximate solutions, such as the tanh− method [3,4], q-homotopy analysis method (q-HAM) [5-7], residual power series method [6], the sub-equation method [6,8,9], improved Bernoulli sub-equation function method [10], the reduced differential transform method [11], the generalized exp
In many previous studies the time-fractional fifth-order Sawada-Kotera equation and the time fractional (4+1)-dimensional Fokas equation have been handled with the sense of Jumarie’s Riemann-Liouville derivative [3,5,6,8,12,19]. Then, solitary solutions have been obtained by creating auxiliary equations in accordance with the method’s own algorithm for the equations, which are reduced by using the traveling wave transformations in the traditional methods applied. These equations, which have important roles in wave theory, are used to explain the physical wave formation structures that occur on the surface and in the water. In particular, whereas Sawada-Kotera equation delineates a merely inelastic scattering transaction, Fokas equation is driven to qualify the surface waves and internal waves in channels or narrows of varying width and depth. The main motivation of this work is to obtain new solitary wave solutions with less computation. Hence, in this study, we apply the newest version of Kudryashov’s algorithm with arbitrary refractive index [30,31] for efficient computation of these equations using the beta derivative.
2 Motivation
2.1 Beta Derivative Definition
Let u be a function,
for all x ≥ a, 0 < α ≤ 1. If the limit of Eq. (1) exists, f is said to be beta-differentiable. Beta derivative definition does not depend on the interval. If the function is differentiable at a zero point Eq. (1) is not equal to zero.
Assuming that, u and v ≠ 0 are two functions beta-differentiable with 0 < α ≤ 1 then, the beta derivative possesses the next properties:
1)
for all a and b real numbers.
2)
with d a given constant..
3)
4)
Considering from Eq. (1) the factor
Introducing
where
3 Methodology
3.1 Methodolgy to figure out the solitary wave solitons
The main steps of the proposed method are represented as follows:
Step 1: Initially, we consider the general form of nonlinear fractional partial differential equations given by
where
Step 2: Secondly, we presume that the following traveling wave transformation
reduces the fractional order of the differential (9) into an ordinary differential equation. Here,
Step 3: By the proposed method, we consider that (12) has a solution of the form:
Where
where
Then, taking into account the polynomial
Step 4: Inserting Eq. (13) and (21)-(25) into 12 we have the reduced form of the
equation into polynomial which consists of Q and
4 Applications
4.1 The time-fractional fifth-order Sawada-Kotera Equation
The time-fractional fifth-order Sawada-Kotera equation is a significant unidirectional nonlinear evolution equation appurtenant a fully integrable hierarchy of higher fractional order KdV equations. In other words, it is a special case of the KdV equations as follows:
where
After this wave transformation, Eq. (26) is reduced into the following ODE:
By using the homogenous balance principle in Eq. (28), balancing the highest order derivative and nonlinear term, we obtain the pole order N = 2. Then, the second degree auxilary polynomial can be written as follows:
Where
adopts the differential equation:
with
Calculating the derivatives of Eq. (29) from first to fifth order the following equations are obtained:
Substituting Eq. (29) and Eqs. (30) into Eq. (28), we obtain an equation which contains the powers of Q. Then, by linking all the same powers of Q and equating all the coefficients to zero, we get the following algebraic system:
Finally, solving this system we get seven cases of solitary wave solutions of the Eq. (26) as:
Case I:
Case II:
Case III:
Case IV:
Case V:
Case VI:
Case VII:
4.2 The (4 + 1)-dimensional space-time fractional Fokas equation
The (4 + 1)-dimensional space-time fractional Fokas equation has the form:
First, we apply the fractional beta transformation:
Then, Eq. (38) is reduced into the following ODE:
We integrate Eq. (41) once, taking the integration constant zero for simplicity. Then, we obtain the following ODE:
Again, using the homogenous balance principle and balacing the terms
Where
adopts the equation:
with
The first and third derivatives of Eq. (43) are sufficient for the solutions. Hence, we take them as follows:
Substituting Eq. (43) and Eqs. (45) into Eq. (42), we get an equation including the powers of Q. Then collecting the terms with the same power of Q and equating the coefficients to zero, we obtain the following algebraic system:
Solving this system we get ten cases of solitary wave solutions of the Eq. (38) as:
Case I:
where
and
Case II:
where
and
Case III:
where
and
Case IV:
where
and
Case V:
where
and
Case VI:
where
and
Case VII:
where
and
Case VIII:
where
and
Case IX:
where
and
Case X:
where
and
5 Concluding Remarks
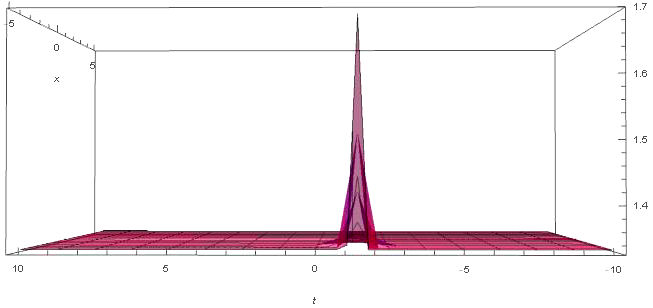
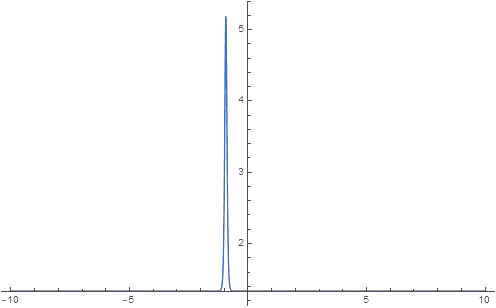
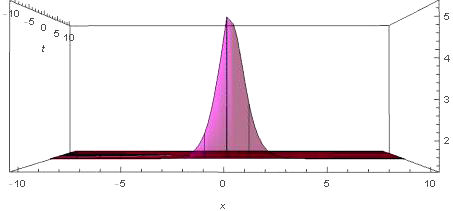
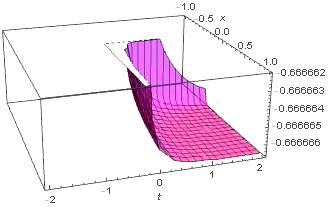
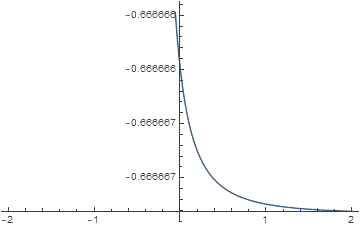
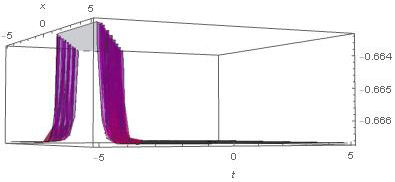
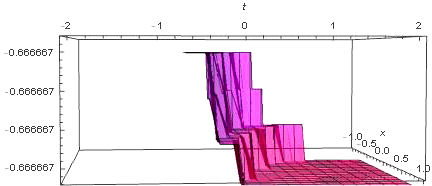
We have applied a new approach of the Kudryashov method to the time-fractional fifth-order Sawada-Kotera equation and the (4 + 1)-dimensional space-time fractional Fokas equation which arise in mathematical physics. The wave transformations applied with the help of beta derivative definitions and the Q function included in the algorithm facilitated the computation of the solutions. The general solutions for the time-fractional fifth-order Sawada-Kotera equation and the (4 + 1)-dimensional space-time fractional Fokas equation have been pointed out as polynomials of the logistic function, which in turn are solutions of the Riccati equation. Finally, some new exact solutions in the form of exponential functions for given equations are established. We have also presented the numerical simulations for equations thanks to three dimensional plots. Therefore, we conclude that this method may have general applications. As comparing the other methods, the advantage of this approach is that the form of function is not used at the calculation. This gives us not only ease of calculation, but also the opportunity to obtain new solutions. However, it should not be overlooked that this new method is more suitable for nonlinear equations with even-order derivatives. Hence, one can conclude that the method can method can be applied to many fractional partial differential equations.
