1. Introduction

The study of nuclear processes induced by weakly bound nuclei such as ⁶Li, ⁷Li, ¹⁰Be, ¹¹Be, has attracted plenary attention for years. Especially, the processes induced by ⁶Li and ⁷Li nuclei gained attention due to the break-up effect of ⁶Li into d + α, and ⁷Li into t + α which plays a crucial role in the elastic scattering of ⁶Li and ⁷Li, for a range of target nuclei at different energies. There are extensive experimental measurements and theoretical studies for ⁶Li + ²⁸Si nuclear system, and the available data are classified into two categories: experimental data near the Coulomb barrier energy EC [¹-⁷] and the data above EC [⁸-¹⁴]. It is appropriate here to disregard particular effects due to coupling to other reaction channels when studying the elastic scattering mechanisms between two ions at energies well above the EC. In this case, the elastic scattering data can be reproduced well by utilizing the conventional optical and folding potentials. On the other hand, at energies near the EC, the coupling effects are significant and appear in various reaction channels. Pakou et al. [¹] measured the angular distributions for ⁶Li + ²⁸Si at four near barrier energies −7.5, 9, 11, and 13 MeV - over a wide angular range. The data were analyzed using optical potential with the real part derived based on double folding (DF) potential. It was found that the strength of the real part of potential remains almost independent of the energy, and in order to reproduce the data, a reduction in the renormalization factor by about 40% is necessary. Sinha et al. [⁵] measured the angular distributions for ⁶Li + ²⁸Si at energies 16 and 21 MeV. The measured data, as well as the data at lower energies, were fitted using optical potentials of both imaginary volume and surface parts. The effect of the break-up on elastic scattering was investigated within the Continuum Discretized Coupled Channels (CDCC) method. Experimental data at high energies [¹⁰-¹⁴] showed refractive features at forwarding angles region, in contrast to the data at low energies close to EC. Nadasen et al. [¹⁴] measured the angular distribution for ⁶Li + ²⁸Si at 318 MeV; the data extend well beyond the rainbow angle into the region where the far-side scattering dominates. The data were reproduced reasonably well using DF potential without renormalization. The data at high energies [⁸-¹⁴] were also subjected to various optical model (OM) and DF analysis. The ⁶Li + ²⁸Si system has been subjected to several theoretical studies [1521] recently, which were devoted to investigating this nuclear system either at low and high energies using different pure OM and DF potentials. M. Anwar [¹⁷] analyzed the experimental angular distributions of ⁶Li scattered elastically by different targets −²⁴Mg, ²⁸Si, ⁴⁰Ca, ⁴⁸Ca, ⁵⁸Ni, ⁹⁰Zr, and ¹¹6Sn - at E _lab (⁶Li) = 240 MeV. The data were analyzed using the conventional OM potential as well as DF of two different effective density independent nucleon-nucleon NN interactions namely S1Y and M3Y. The analysis incorporated four different forms of ⁶Li density distribution with rms radii ranging from 2.195 to 2.444 fm. The DF analysis, for the concerned data, showed that the strength of the real part of potential should be reduced by a factor of ≈ 28% - 0.36%. M. A. Hassanain et al. [¹⁹] investigated the ⁶Li + ²⁸Si elastic scattering at six energy sets ranging from 76 to 318 MeV, using two approaches. In the first approach, the full α cluster structure of the interacting nuclei was considered, where ⁶Li was described in terms of d−α cluster model wave function, and the ²⁸Si nucleus was described as 7α. In the second approach, the real part of the potential was constructed based on the CDM3Y6 Paris NN interaction. They reported that the quality of fitting directly proportional to the energy, as expected, and a renormalization factor of ≈ 0.43 − 1.0 is required to fit the data.

Yongli Xu et al. [²¹] performed a systematic global optical model description for ⁶Li projectiles scattered elastically from targets ranging from ²⁴Mg to ²⁰⁹Bi at energies below 250 MeV. The obtained global optical potential from this study was found to be applicable for different elastic scattering processes induced by ⁶Li. The obtained potential is also used to predict the reaction cross sections for targets outside the concerned mass range.

Y. Sakuragi [²²] studied the projectile break-up effects on the elastic scattering of ⁶Li from different targets with a mass number (α = 12 − 208). The ⁶Li break-up effects were investigated, within the framework of the CDCC method, in the elastic scattering cross-sections with interaction potentials extracted from the M3Y DF potential. The calculations could reproduce the experimental elastic scattering data for all the studied targets and incident energies without any renormalization for the folded potential if an additional term “Dynamic Polarization Potential DPP” was introduced. The DPP has a repulsive real part with a strength of ≈ 40% of the folding potential. For nucleons, α−particles and heavy ions (α _P ≥ 10), at energies up to 20 MeV/nucleon, the folding potential is successful in fitting the experimental data with N _R ≈ 1.0. However, the optical potential for ^6,7 Li [²²-²⁶], based on a folding model, has been found unsuccessful since the values of N _R required in order to fit the data are much smaller than unity. Theoretical studies for ⁶Li-target systems present a problem in the DF model description, where the real potential requires a renormalization of approximately one-half in order to reproduce the data. Branden et al. [²⁷] assumed that this is due to the importance of break-up channels for the loosely bound ⁶Li nucleus, represented by a complex DPP, which has a strongly repulsive real part. It is to be noted that several theoretical calculations [²²,²⁸,²⁹], including CDCC calculations, showed that the renormalization factor is close to unity when the coupling to break-up channels is included.

The available experimental measurements for ⁶Li + ²⁸Si system at high energies and over sufficiently wide angular range reveal several ambiguities associated with the different concerned potentials. In the present work, the ⁶Li + ²⁸Si nuclear system is subjected to further investigation. Firstly, a new systematic global description for the data is obtained using the conventional OM potential of fixed radii parameters. Secondly, motivated by the well-known cluster nature of ⁶Li, the data are reanalyzed from the microscopic point of view in the cluster folding optical model (CFOM) framework. The ⁶Li + ²⁸Si angular distributions data are plotted as a function of momentum transfer, and they showed that the same real part of potential could be used to reproduce the data at different energies as they exhibit the same oscillatory behavior in the forward angle region. Finally, the concerned data are well described using non-renormalized real cluster folding potential when an additional dynamical polarization term is added.

The paper is organized as follows. In Sec. 2, the theoretical calculations for ⁶Li + ²⁸Si system based on both optical and cluster folding potentials are described. Section 3 is devoted to the discussion of the results and the summary is given in Sec. 4.

2. Theoretical calculations

Using the phenomenological OM potential and semi microscopically using CFOM potential, the elastic scattering angular distributions for ⁶Li + ²⁸Si nuclear system in the energy range 16 − 318 MeV are reanalyzed in order to obtain the global potential, which could reproduce the data in this wide range of concerned energies.

2.2. Data analysis within the framework of CFOM

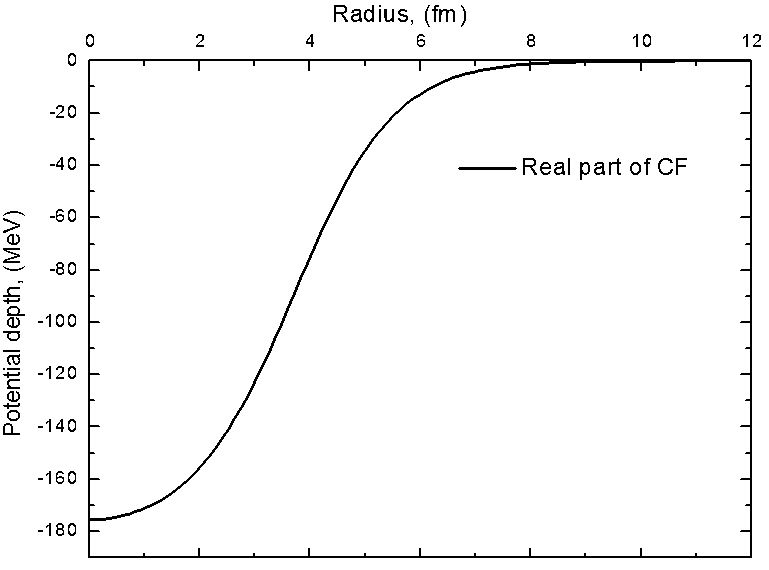
Considering the appreciable cluster probability of ⁶Li as a weakly bound α + d system, we try to describe the ⁶Li elastically scattered from ²⁸Si nucleus using a simple CFOM. In this model, the real part of ⁶Li + ²⁸Si potential is generated based on cluster folding. For the well-known optical potential of α−particles and deuterons, we define the ⁶Li potential as:

VCF(R)=∫Vα-28SiR-13r+Vd-28SiR+23r|χαd(r)|2dr, (3)

where χ _αd (r) is the intercluster wave function for the relative motion of α and d in the ground state of ⁶Li, and r is the relative coordinate between the centers of mass of α and d. Vα-28Si and Vd-28Si are the phenomenological potentials for α + ²⁸Si and d + ²⁸Si channels which fairly reproduce the experimental data at the appropriate energies E _d ≈ 1/3E _Li and E _α ≈ 2/3E _Li taken from [31,32]. α − d bound state form factor represents a 2S state in a real WS potential with V ₀ = 79.0 MeV, R = 1.15 fm, α = 0.7 fm [³³]. The main parameters required to prepare the cluster folding potential for ⁶Li + ²⁸Si are the optimal potentials for d + ²⁸Si and α + ²⁸Si at appropriate energies. The highest energy under consideration is 318 MeV, so the required potentials are Vd+28Si at E _lab = 1/3 × 318 = 106 MeV and Vα+28Si at E _lab = 2/3 × 318 = 212 MeV. Unfortunately, there are no experimental measurements at the aforementioned energies. For the second maximum available data for ⁶Li + ²⁸Si (240 MeV), the required potentials are V _d+ 28_Si at E _lab = 80 MeV and V _α+ 28_Si at E _lab = 160 MeV. By searching the previous experimental studies for d + ²⁸Si and α + ²⁸Si nuclear systems, it is found that the most suitable potentials, which could be used to generate the cluster folding potential for ⁶Li + ²⁸Si are d + ²⁸Si at E _lab = 52 MeV [³¹] and α + ²⁸Si at E _lab = 166 MeV [³²]. The obtained real part for the generated cluster folding potential is presented in Fig. 1.

FIGURE 1 Real cluster folding potential used in the present study. 

3. Results and discussion

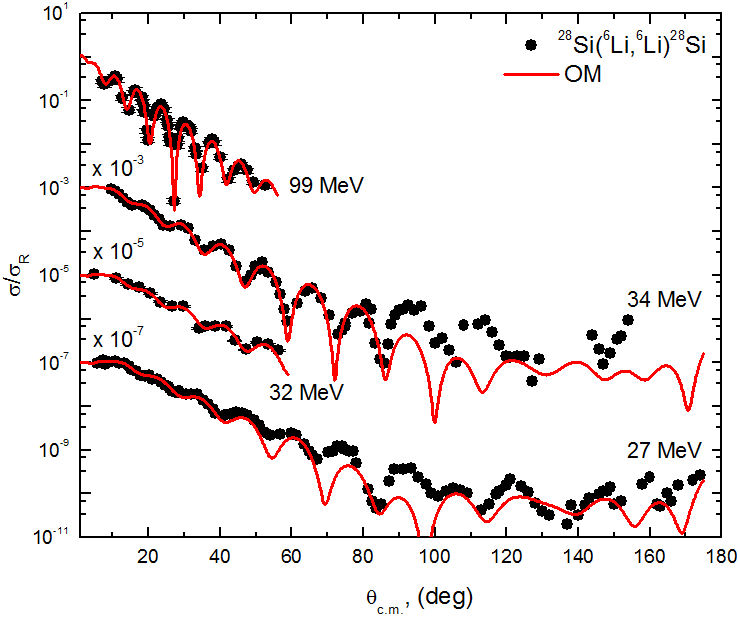
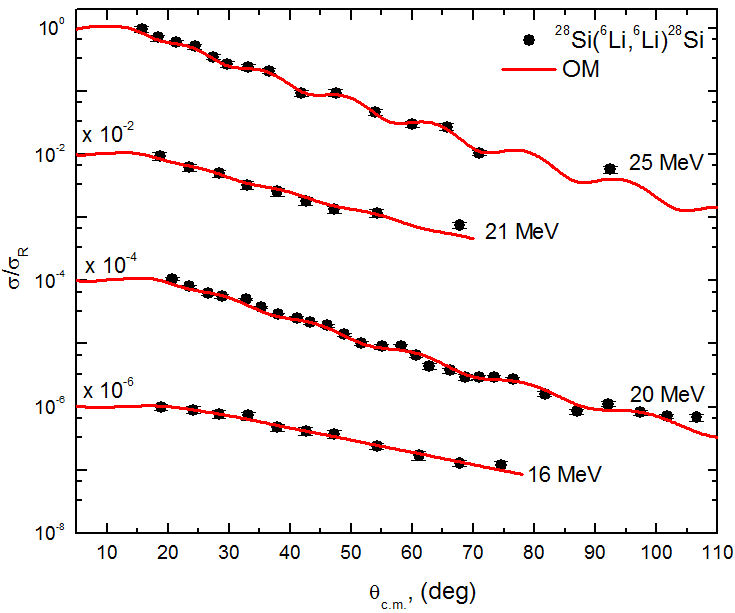
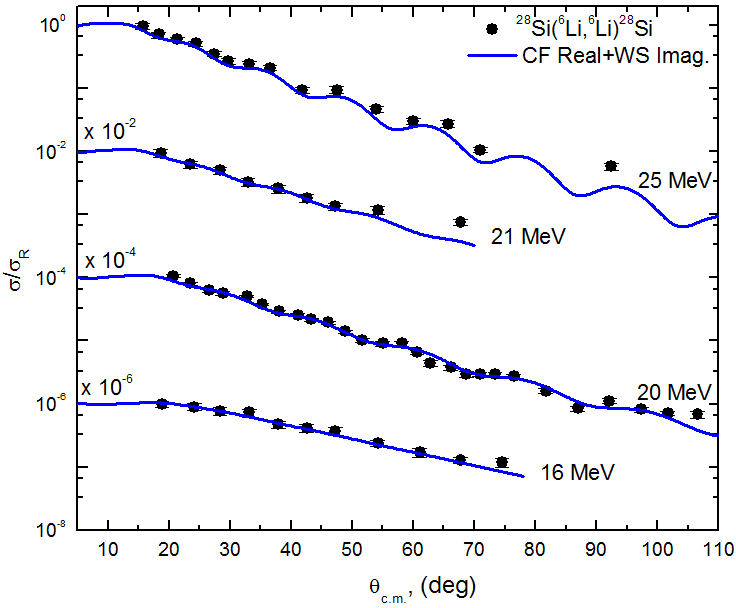
The comparison between the experimental ⁶Li + ²⁸Si elastic scattering angular distributions at E _lab = 16 − 318 MeV and the theoretical calculations based on Woods-Saxon optical potential are shown in Figs. 2-4 and the extracted potential parameters are listed in Table I. The agreement between the experimental data and calculations is fairly good not only at all the concerned energies but also over the entire angular range. The χ ² /N values obtained from this work are comparable to previously reported values [⁵-¹⁴]. Although the radius parameter for both the real and imaginary potential parts are fixed during the search process for potential parameters, no clear dependence of real and imaginary potential depths on energy is obtained.

FIGURE 2 Comparison between experimental angular distributions data (solid black circles) and theoretical calculations for ²⁸Si(⁶Li,⁶Li)²⁸Si elastic scattering at E _lab = 318, 240, 210, and 135.1 MeV. The solid red curves denote OM fits. 

FIGURE 3 Same as Fig. 2 but at E _lab =99, 34, 32, and 27 MeV. 

FIGURE 4 Same as Fig. 2 but at E _lab =25, 21, 20, and 16 MeV. 

In CFOM, the theoretical calculations are performed using a real part of the potential derived based on mentioned cluster folding “see Eq. (3)” in addition to an imaginary Woods-Saxon term. Thus, the nuclear potential takes the following shape:

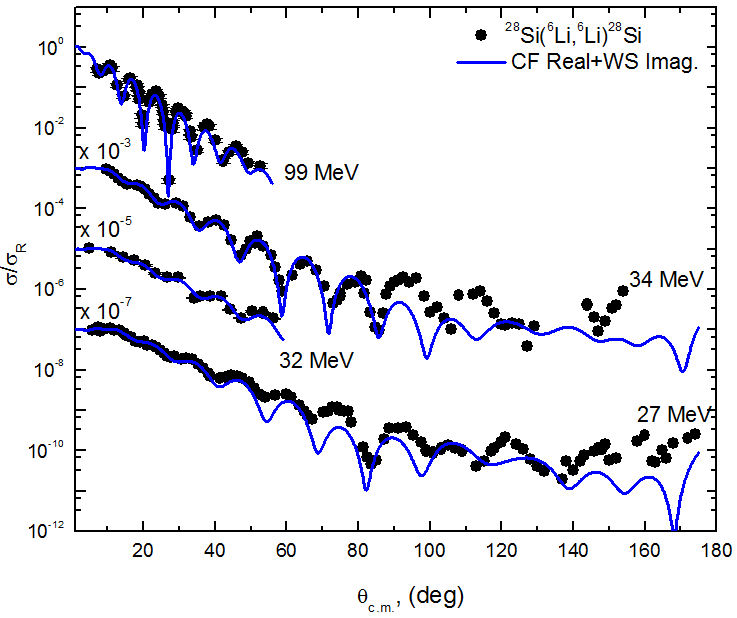
The comparison between the experimental angular distributions for ⁶Li + ²⁸Si elastic scattering and the theoretical calculations performed within the framework of CFOM are shown in Figs. 5-7, while the potential parameters are listed in Table II. The same potential parameters for the imaginary volume term, extracted from the OM analysis, are kept the same in CFOM calculations. Consequently, the data are fitted using only one parameter- N _RCF , “which is the renormalization factor for the real part of potential derived based on cluster folding”. As shown in Figs. 5-7, the agreement between the experimental data and the calculations is good, and the χ ² /N values are close to those obtained from OM analysis or even better at some energies. The extracted average value for N _RCF is 0.732±0.1, indicating that the strength of N _RCF should be reduced by about 27% in order to reproduce the data. The same problem was reported previously in DF analysis for ⁶Li + X nuclear systems, where X is a different target nucleus such as ¹²C, ¹⁶O, ²⁸Si.

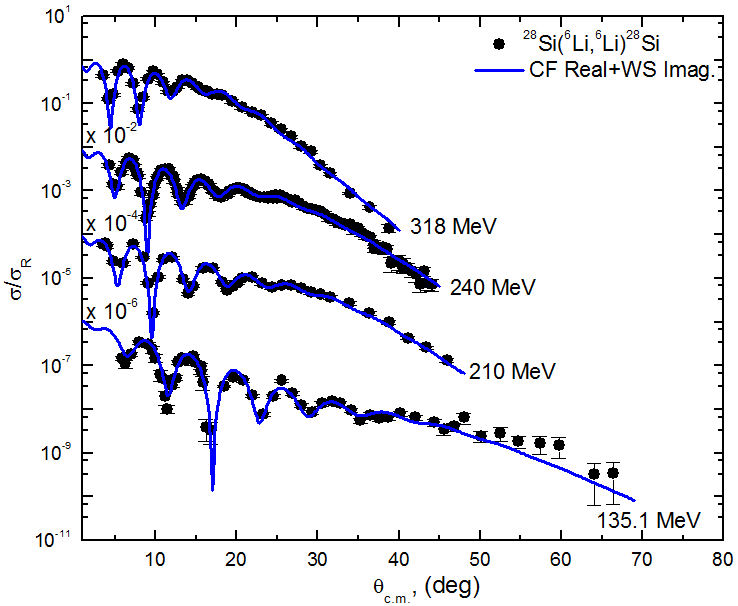
FIGURE 5 Comparison between experimental angular distributions data (solid black circles) for ²⁸Si(⁶Li,⁶Li)²⁸Si elastic scattering and the theoretical calculations (solid blue curves) using CFP plus an imaginary WS potential at E _lab = 318, 240, 210, and 135.1 MeV. 

FIGURE 6 Same as Fig. 5 but at E _lab =99, 34, 32, and 27 MeV. 

FIGURE 7 Same as Fig. 5 but at E _lab =25, 21, 20, and 16 MeV. 

The elastic scattering angular distributions for the ⁶Li + ²⁸Si nuclear system at the different concerned energies are plotted as a function of momentum transfer as shown in Fig. 8. The data at relatively higher energies displayed a complex oscillatory behavior with periodic structures of different periods at forwarding angles. The interference peaks and valleys line up, whereas if they are plotted as a function of angle, there is not an apparent pattern. The formula q = 2k sin(θ _c.m /2) is used to calculate the cross-sections as a function of momentum, where k is the wavenumber. The wavenumber was taken to be k=0.219[MtMt+Mp]xMp×Elab. Here M _p and M _t are the masses of the projectile and target, respectively. As shown in Fig. 8, the plotted data, as a function of momentum transfer, exhibit dips form at momentum transfers around q = 0.59, 1.05, and 1.58 fm⁻¹ that can be followed down to an energy of 34 MeV. Consequently, it should be shown that the forward angle dips are produced by the same “potential”; and the differences between the cross-sections at different energies at larger momentum transfer (angles) are due to the absorption at larger values. This is also the reason why the data at lower energies (below 16 MeV) are excluded from this study. The extracted values of N _RCF from the CFOM at the different concerned energies are close to each other except for the data for the data at lower energies, which showed some deviations as shown in Table II. Therefore, if N _RCF is adjusted to 0.732 -the average extracted value from CFOM analysis and is allowed for a slight variation for W ₀ and α _W , the data could be reproduced with the same real cluster folding potential.

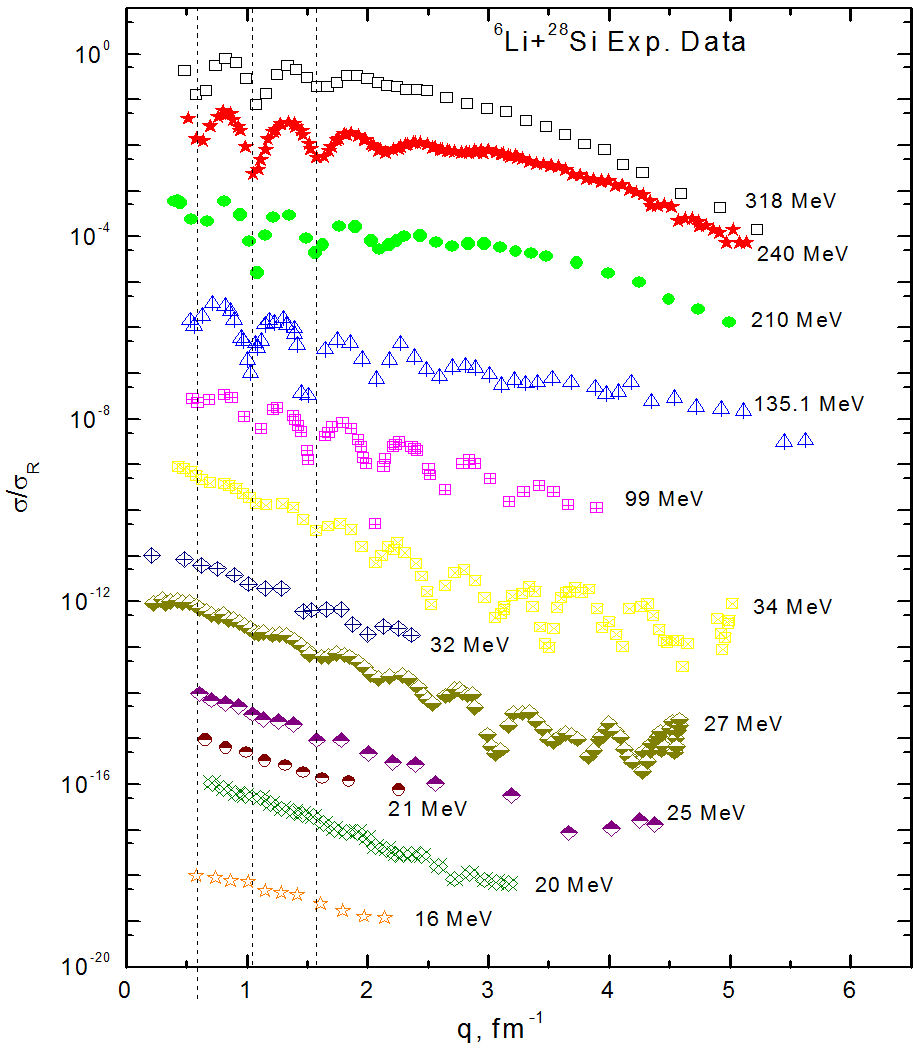
FIGURE 8 Experimental angular distributions for ⁶Li + ²⁸Si elastic scattering at energies E _lab =16−318 MeV plotted as a function of momentum transfer. 

The strong absorption at relatively high energies leads to refractive features such as the nuclear rainbow followed by structure-less falloff, as shown in Fig. 8. The possibility of seeing such refractive features was first realized in the scattering of alpha particles [³⁴]. A few years later, hints emerged that similar but weaker effects were seen in the scattering of light heavy-ions ⁶Li [¹¹,³⁵] and ¹²C [³⁶,³⁷]. By now, many examples of refractive phenomena in light heavy-ion systems have been collected already.

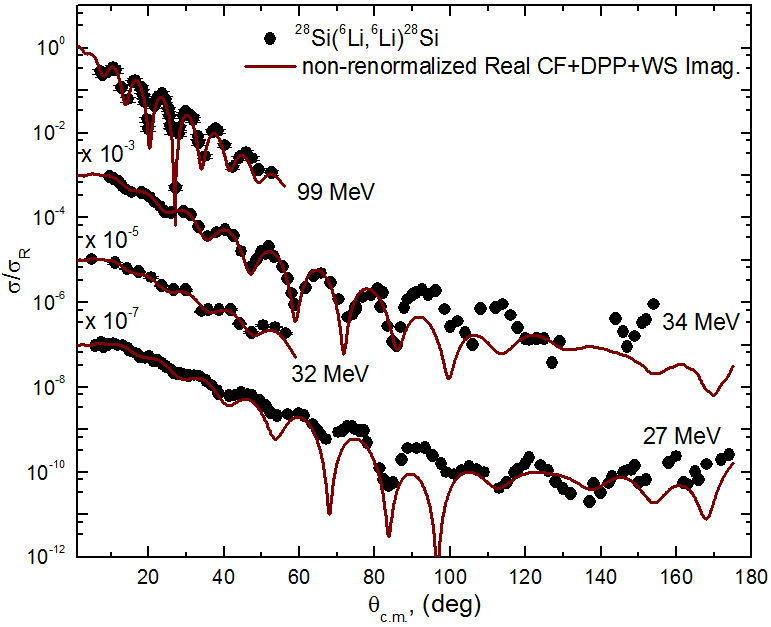
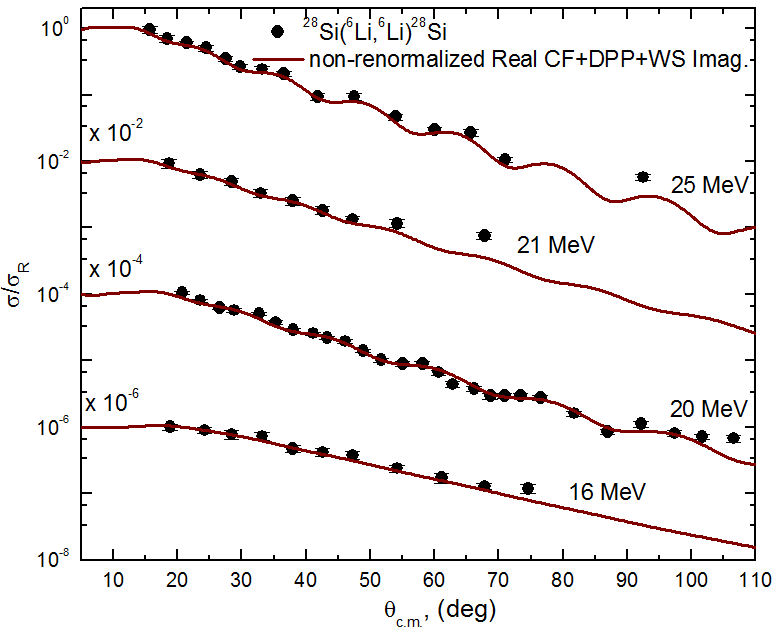
Previously microscopic analysis for the ⁶Li + ²⁸Si system presented a problem in the DF, where the real part of potential required a renormalization of approximately one-half in order to reproduce the data, and it was assumed that this is due to the importance of break-up channels for the loosely bound ⁶Li nucleus. The analysis of ⁶Li + ²⁸Si scattering data using real CFP in the current work also showed the same trend, as N _RCF should be reduced by about 27% in order to reproduce the data. The cluster folding calculations are repeated using non-renormalized real CFP “N _RCF = 1” with the same, previously obtained imaginary WS potential plus a dynamical polarization potential (surface potential with a repulsive real part designed to simulate the polarization effects caused by the projectile break-up). The used DPP is characterized by three parameters (V _pol, r _pol, α _pol), and their corresponding values at the different concerned energies are listed in Table III. The comparisons between the experimental data and theoretical calculation performed using the non-renormalized real CFP plus the dynamical polarization potential are shown in Figs. 9-11, and they show the same good agreement as in Figs. 5-7.

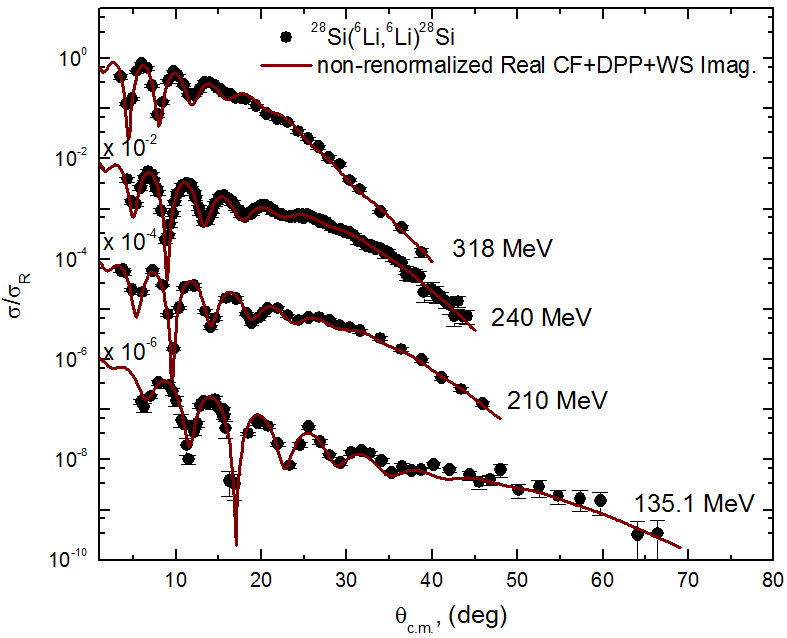
FIGURE 9 Comparison between experimental angular distributions data (solid black circles) for ²⁸Si(⁶Li,⁶Li)²⁸Si elastic scattering and the theoretical calculations (solid brown curves) using nonrenormalized real CFP plus a DPP term in addition to an imaginary WS potential at E _lab =318, 240, 210, and 135.1 MeV. 

FIGURE 10 Same as Fig. 9 but at E _lab =99, 34, 32, and 27 MeV. 

FIGURE 11 Same as Fig. 9 but at E _lab =25, 21, 20, and 16 MeV. 

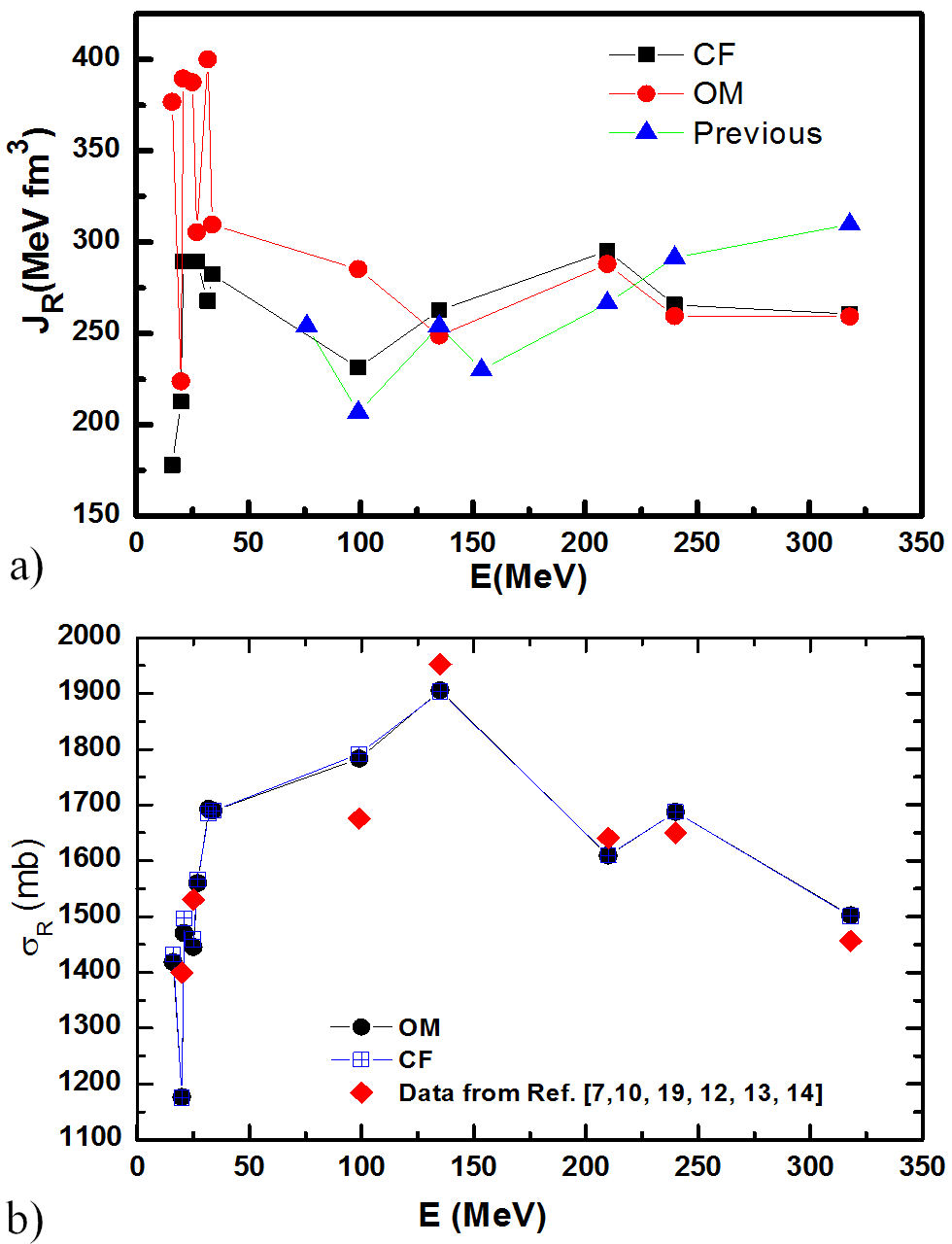
The best-fitting OM and CFOM parameters, with the corresponding calculated real and imaginary volume integrals per interacting nucleon pair (J _R and J _i ) as well as the total reaction cross sections σ _R in mb, are presented in Tables I and II, respectively. The extracted values for the total reaction cross-section σ _R as well as the real volume integral are described graphically in Fig. 12. As shown in this figure, the σ _R for CF and OM potentials has approximately the same energy behavior. After comparison, we found that the extracted values of σ _R and J _R are in good agreement with the previously reported values from Refs. [⁷,¹⁰,¹²-¹⁴,¹⁹].

FIGURE 12 Energy dependence of the reaction cross-sections as well as real volume integral extracted from OM and CF calculations and compared with the available data from Refs. [⁷,¹⁰,¹²-¹⁴,¹⁹]. 

4. Summary

The experimental angular distributions for ⁶Li + ²⁸Si at E _lab = 16 − 318 MeV are reanalyzed using Woods- Saxon OM potential consisting of four varying parameters −V ₀, α _V , W ₀, and α _W depth and diffuseness for both the utilized real and imaginary volume terms while, the radii parameters −r _V and r _W were kept fixed. The agreement between the experimental data and the theoretical calculations is reasonably good not only at the different concerned energies but also over the entire angular range. These data are also reanalyzed within the framework of CFOM. In this model, the real part of the potential was constructed on the basis of cluster folding, while the imaginary part was taken in the WS form as in OM analysis using the same parameters. In this case, the data are fitted with only one parameter- N _RCF . The obtained average value of N _RCF is 0.732 ± 0.1, suggesting that the strength of N _RCF should be reduced by about 27% in order to reproduce the data. The same problem was reported previously in DF analysis for the ⁶Li + ²⁸Si nuclear system. Calculations performed using non-renormalized real CFP, “i.e, N _RCF = 1” could reproduce the data fairly by introducing a DPP surface potential term with a repulsive real part to simulate the polarization effects caused by ⁶Li break-up. Finally, the experimental data for the ⁶Li + ²⁸Si nuclear system, plotted as a function of momentum transfer, showed interference peaks and valleys line up and exhibit dips form at the momentum transfers around q = 0.59, 1.05, and 1.58 fm⁻¹ that can be followed down to an energy of 34 MeV. Consequently, it should be shown that the forward angle dips are produced by the same “potential” and the differences between the crosssections at different energies, at larger momentum transfer (angles), are due to the absorption at larger values.