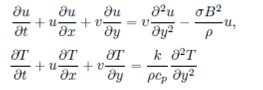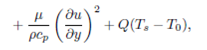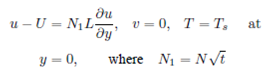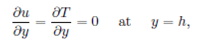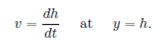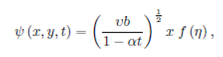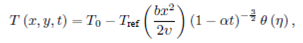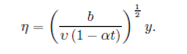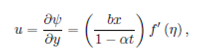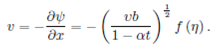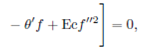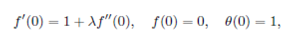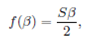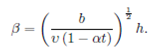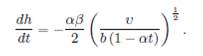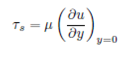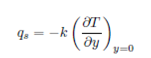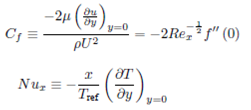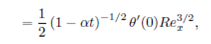1. Introduction

Boundary layer flow and heat transfer over a thin liquid film on an unsteady stretching sheet has received considerable attention from researchers because of their numerous practical applications in many applications, like coating process and design of various heat exchangers and chemical processing equipments, wire and fiber coating, food stuff processing reactor fluidization and transpiration cooling.

The study of flow and heat transfer caused by a stretching surface is of great importance in many manufacturing processes such as extrusion process, glass blowing, hot rolling, manufacturing of plastic and rubber sheets, crystal growing, continuous cooling and fibers spinning^1,2. In all these cases, a study of flow field and heat transfer can be of significant importance because the quality of the final product depends to a large extent on the skin friction coefficient and the surface heat transfer rate.

Boundary layer flow past a stretching sheet is applicable to viscous and some viscoelastic fluid flows with usual no-slip flow boundary condition over many stretching types such as linear and exponential stretching and a small attention is given to slip boundary condition, though slip boundary conditions finds prominent applications in various fields of science and technology, but fluids with micro-scale or nano-scale dimensions have flow behavior which is completely different from usual fluid behavior, and definitely it belongs to slip flow. So even in case of slip flow regime, the fluid motion depends on Navier-Stoke’s equations, with slip velocity, temperature and concentration boundary conditions. Slip flow finds applications in case of micro/nano systems, such as micro-pump, micro-valve and micro-nozzles,which agrees with slip condition at the boundary wall. The no-slip boundary condition is the main theory concerned to Navier-Stoke’s equations in fluid dynamics. But in some situations, where in case of viscoelastic fluids such no slip conditions does not hold good for study of fluids in motion. No slip condition cannot be applied, to various viscoelastic and many other liquids, which does not obey Newton’s viscosity postulate, such as nanofluids, polymer melt generally shows microscopic wall slip and in general is governed by a monotone relation between slip velocity and the traction. The liquids that slips at boundary finds applications in various technological problems such as in polishing of artificial heart valves and internal cavities.

Sakiadis^3,4 investigated the flow due to a sheet issuing with constant speed from a slit into a fluid at rest. This flow was of Blasius type, in which the boundary layer thickness increased with the distance from the slit. Sarpakaya⁵ was the first researcher to study the MHD flow of a non-Newtonian fluid. Prandtl’s boundary layer theory proved to be of great use in Newtonian fluids as Navier-Stokes equations can be converted into much simplified boundary layer equation which is easier to handle.

McCormack and Crane⁶ gave a similar solution in a closed analytic form for the two dimensional stretching of a flat surface with a velocity proportional to the distance from the slit. In a pioneering work, Crane⁷ considered the steady two-dimensional flow of a Newtonian fluid caused by a stretching elastic flat sheet which moves in its own plane with a velocity varying linearly with the distance from a fixed point. This work is extended by many authors to investigate various aspects of the flow and heat transfer occurring in the different domains of the fluid, see^8-13. Wang , Usha and Sridharan , Chen^16,17, Kumari and Nath , Andersson et al.^19,20, Dandapat et al.^21,22 and Dandapat and Ray . In the pioneering work of Wang , the flow of a Newtonian fluid in a thin liquid film past an unsteady stretching sheet was investigated. He reduced the unsteady Navier-Stokes equations to a nonlinear ordinary differential equations by means of similarity transformation and then solved the same using a kind of multiple shooting method (see Robert and Shipman ). The results in were extended by several authors for Newtonian and non-Newtonian fluids using various velocity and thermal boundary conditions^19-26. Aziz et al. have neglected the magnetic field effect and also used the homotopy analysis method for thin film flow and heat transfer on an unsteady stretching sheet with internal heating.

Many researchers devoted to the study concerned to slip flow regime for more than a decade, see for example Refs.^27,28. To mention a few are, Andersson 32 obtained a closed form solution for fully developed, Navier-Stokes equations, considering the effect of magnetic field, over a stretching sheet. Again, Wang found the closed form similarity solution of a complete Navier-Stoke’s equations for the flow, produced by stretching of an elastic sheet, with slip effects. Furthermore, Wang investigated slip flow and heat transfer at a stagnation point past a moving plate. Fang et al. considered the study of slip flow over a moving plate with the effect of magnetic field, and obtained the solution of the resulting boundary value problem analytically. Hayat et al. extended the problem of various other researchers considering the effect of thermal slip condition in addition to velocity slip condition for flow and heat transfer over a stretching sheet, for which suction/injection, are taken into account. Similarly, Aziz studied momentum and thermal slip boundary conditions for boundary layer flow over a flat plate, with constant heat flux boundary condition. Further recent details of the slip effects can be found in Refs.^33-37.

In the literature, there are extensive studies regarding the production of thin liquid film, see for example [38-42], either on a vertical wall achieved through the action of gravity. If the fluid is very viscous, considerable heat can be produced even though at relatively low speeds, e.g. in the extrusion of plastic, and hence the heat transfer results may alter appreciably due to viscous dissipation. Taking into account this point, Abel et al. have investigated the influence of viscous dissipation on heat transfer in a finite liquid film over a continuously moving surface. They showed that the combined effect of magnetic field and viscous dissipation is to enhance the thermal boundary layer thickness.

The main purpose of the present study is to extend the results of by considering the velocity slip effects on the viscous dissipation and internal heat generation for MHD flow and heat transfer in a thin liquid film on an unsteady stretching sheet. Appropriate similarity transformations are applied to convert the governing partial differential equations into a system of non-linear ordinary differential equations, which are to be solved by shooting technique with fourth order Runge-Kutta method. The obtained numerical results are compared with whose published ones in some limiting cases. Then, the influence of the investigated parameters are plotted and discussed.

2. Mathematical Formulation

2.1 Description of the problem

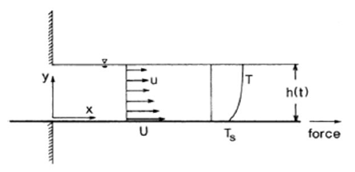
In the present study, we consider a thin elastic liquid film of uniform thickness h(t) lying on the horizontal stretching sheet as shown in Fig. 1, where the sheet is set in motion along 𝑥-axis and the stretching occurs by the action of two equal and opposite forces along this axis. In addition, the fluid motion within the film is primarily caused solely by this stretching. Velocity of the sheet 𝑈 is defined as

Ux,t=bx(1-αt)

where 𝑏 and 𝛼 are positive constants with dimension of the time 𝑡. This expression reflects the effective stretching rate 𝑏/(1−𝛼𝑡) increase with time in the range 𝛼 values, where 0≤𝛼<1. By the same manner, the surface temperature 𝑇 𝑠 (𝑥,𝑡) is expressed by

Tsx,y=T0-Trefbx22v1-αt-32

where 𝑇 0 is the temperature at the slit, 𝑇 ref can be taken as a constant reference temperature such that 0≤ 𝑇 ref ≤ 𝑇 0 and 𝜐 is the kinematic viscosity. Eq. ([eq:2]) showed that the sheet temperature decreases from 𝑇 0 and the amount of temperature reduction along the sheet increases with time. Further, it is considered that the flow field is exposed to the influence of an external transverse magnetic field of strength 𝐵 0 expressed by

Figure 1 Schematic representation of a liquid film on an elastic sheet. 

Bx,t=B01-αt-12

It is also assumed that induced magnetic field, effect of the surface tension, latent heat due to evaporation, surface waves and buoyancy are neglected. Furthermore, we considered that the viscous shear stress 𝜏=𝜇( 𝜗 𝜗𝑦 ) and the heat flux 𝑞=𝑘( 𝜕𝑢 𝜕𝑦 ) vanish at the adiabatic free surface (at 𝑦=ℎ),

2.4 Quantities of practical interest

The most important characteristics of flow and heat transfer are the shear stress 𝜏 𝑠 and the heat flux 𝑞 𝑠 on the stretching sheet that are defined as

(22)

Table 1 Comparison of values of skin friction coefficient f00(0) with Mn = 0:0. 

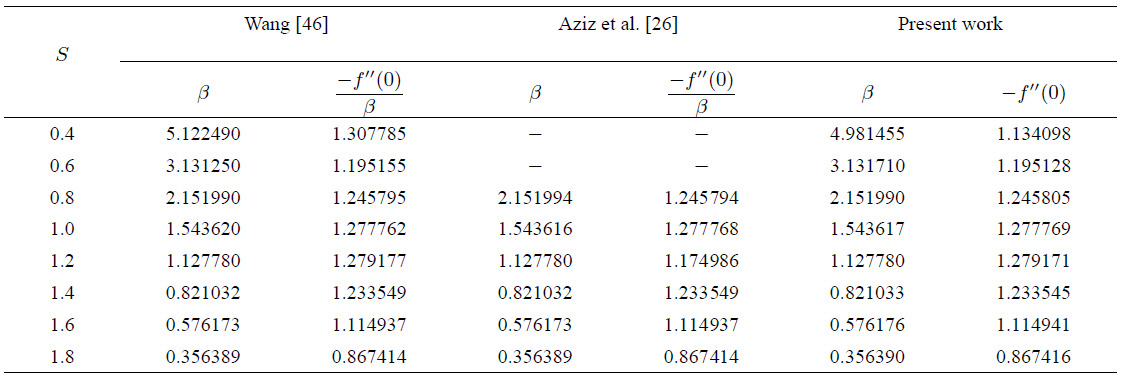
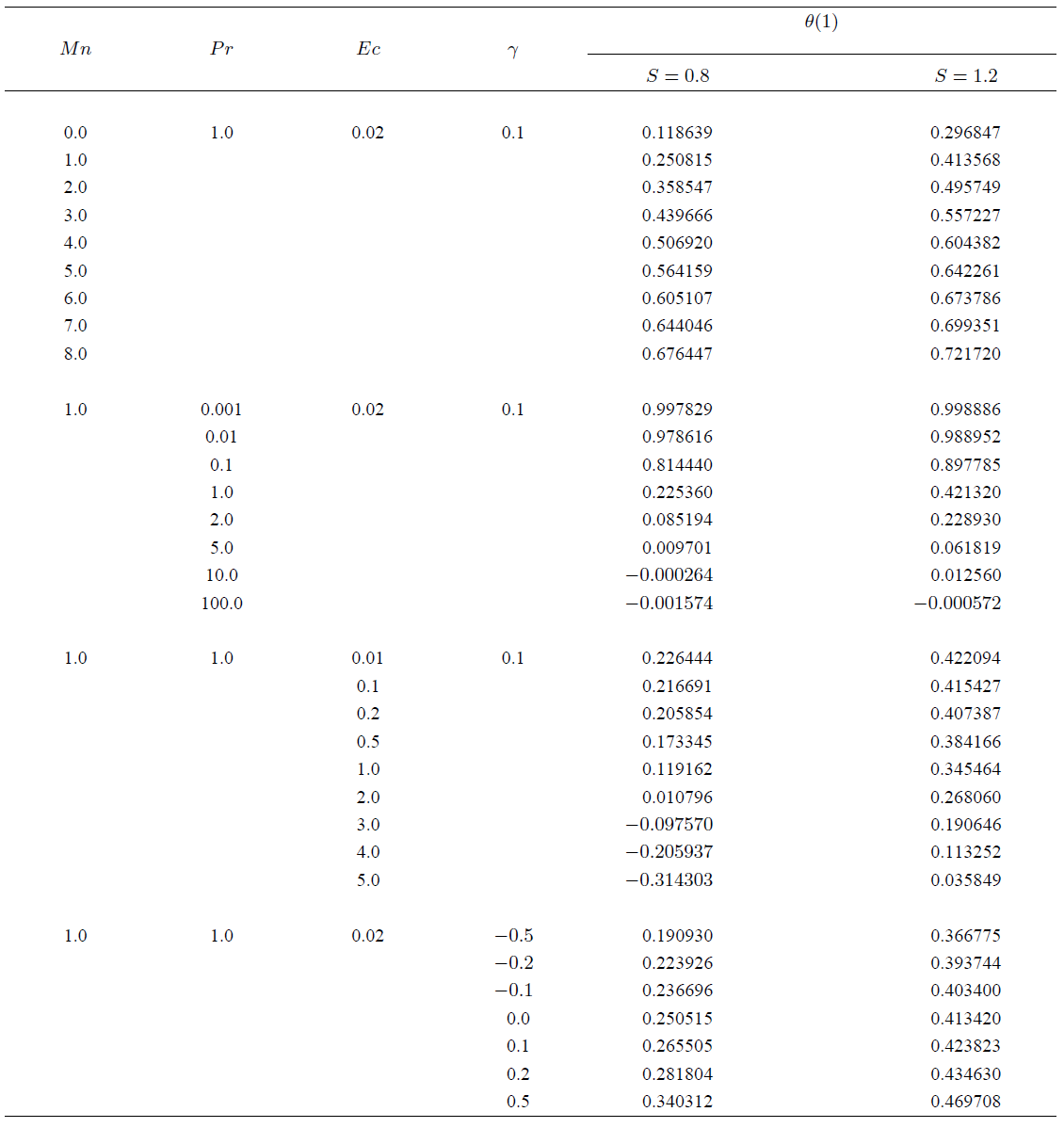
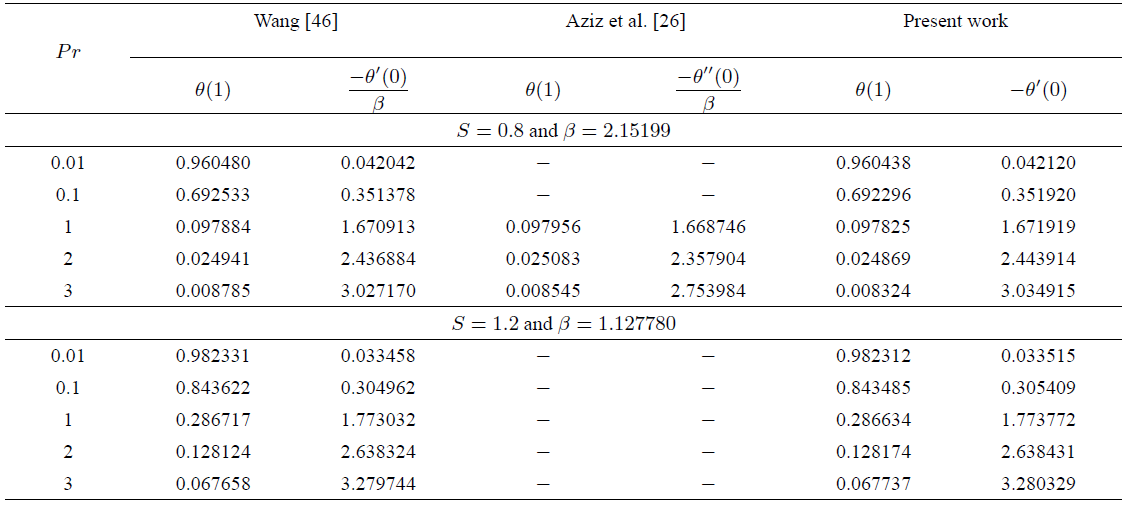
Table 2 Comparison of values of surface temperature µ(1) and wall temperature gradient ¡µ0(0) with Mn = Ec = ° = 0:0. 

(23)

The local skin friction coefficient 𝐶 𝑓 and the local Nusselt number 𝑁 𝑢 𝑥 for fluid flow in a thin film can be expressed as

(24)

(25)

where 𝑅 𝑒 𝑥 (=𝑈𝑥/𝜐) is the local Reynolds number and 𝑇 ref denotes the same reference temperature (temperature difference) as in Eq. (2).

3. Numerical technique

Due to the non-linear form of the resulting momentum and thermal boundary layer equations (15) and (16) with boundary conditions (17-19) are numerically solved by shooting technique with fourth order Runge-Kutta method. The present BVP is equivalent to a system of five first order differential equations with six boundary conditions, where the crucial part of the numerical solution is to determine the dimensionless film thickness 𝛽. Eqs. (15) and (16) are integrated by fourth order Runge-Kutta scheme from 𝜂=0to𝜂=𝛽 with 𝑓(0)=0, 𝑓 ′ (0)=1and𝜃(0)=1 and guessed the trial values, 𝑓″(0), 𝜃′(0) and 𝛽. However, the numerical solution thus obtained does not generally satisfy the right-end boundary conditions, 𝑓″(𝛽)=0, 𝜃′(0)=0 and 𝑓(𝛽)=𝑆𝛽/2. At this end, Newton-Raphson scheme is employed to correct the three arbitrary guess values such that the obtained solution eventually satisfies the required boundary conditions (18) and (19).

Table 3 Values of surface temperature µ(1) for various values of Mn, Pr, Ec, ° and S. 

It should be mentioned here that the iterative process is terminated until the relative difference between the current and the previous iterative values of 𝑓(𝛽) matches with the value of 𝑆𝛽/2 up to a tolerance of 10 −6 . For further details on the numerical procedure, the readers are referred to Refs.⁴⁴,⁴⁵ and ⁴³.

4. Results and discussion

In the current study, effects of the velocity slip on the viscous dissipation and internal heat generation for MHD flow and heat transfer in a thin liquid film on an unsteady stretching sheet has been investigated. Then, appropriate similarity transformations were adopted to convert the governing partial differential equations of flow and heat transfer into a system

Figure 2 Velocity profiles for various values of the slip parameter¸ with S = 0. 

Figure 3 Variation of the film thickness ¯ with unsteadiness parameter S when Mn = 0. 

tem of non-linear ordinary differential equations. Shooting technique with fourth order Runge-Kutta method has been applied to solve the resultant boundary value problem, where the solution exists only when 0≤𝑆≤2. It should be mentioned here that, although the present results are considered as an extension of those obtained in Ref. ⁴³ by applying the velocity slip parameter 𝜆, effects of various parameters influencing the dynamics should be reinvestigated because 𝜆 presents in the conditions of 𝑓-equation [eq:15] which is already included in the 𝜃-equation [eq:16]. These effects are depicted in Figs. 2 to 13.

On comparing with some published works, Tables I and II show an excellent agreement between the present results and those of Wang⁴⁶ and Aziz et al.²⁶. However, it should be noted that they have used different similarity transformations due to which the values of 𝑓″(0)/𝛽 and −𝜃′(0)/𝛽 in their papers are the same as 𝑓″(0) and 𝜃′(0), respectively, of the present results.

Figure 4 Variation of surface temperature µ(¯) with the magnetic parameter Mn. 

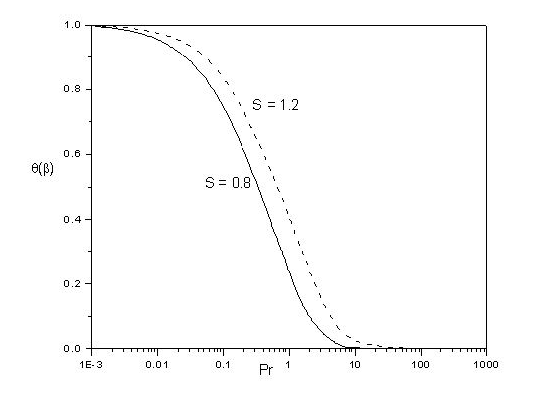
Figure 5 Variation of surface temperature µ(¯) with Prandtl number Pr for S = 0:8 (the solid curve) and S = 1:2 (the dotted curve). 

Figure 6 Variation of surface temperature µ(¯) with Eckert number Ec. 

Figure 7 Variation of surface temperature µ(¯) with heat source/sink parameter Q. 

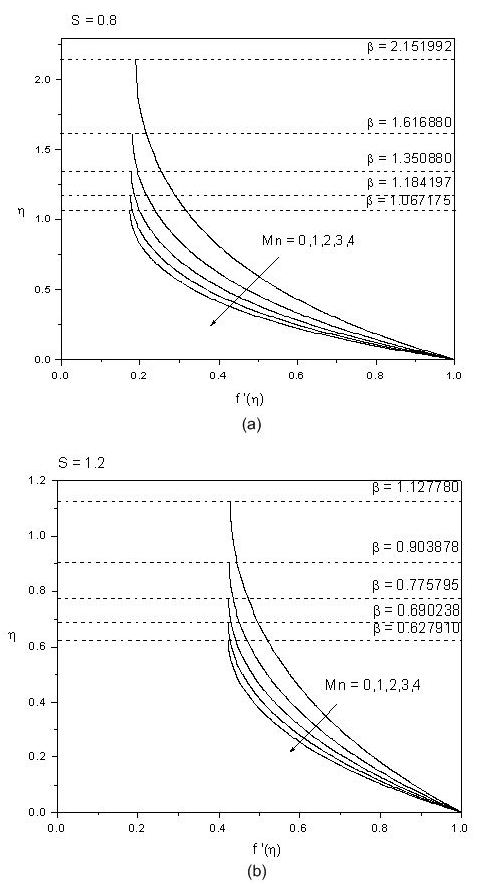
Figure 8 Variation of the velocity profiles f0(´) for different values of the magnetic parameter Mn when (a) S = 0:8 and (b) S = 1:2. 

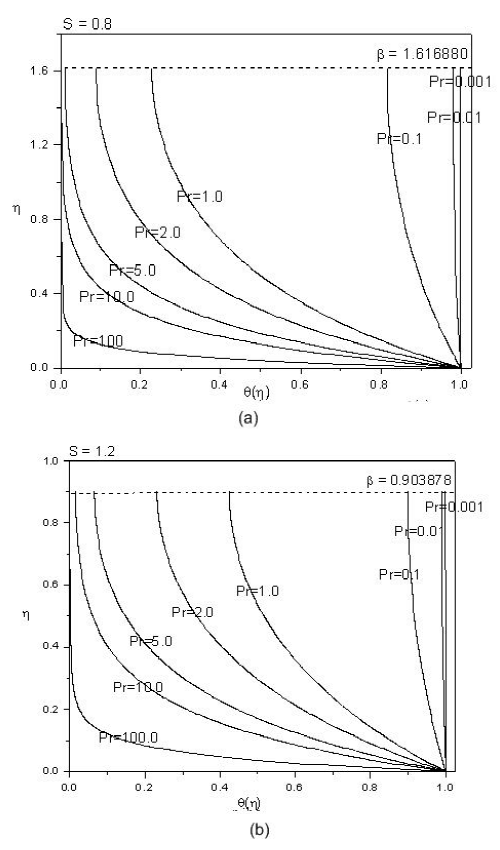
Figure 9 Variation of the temperature distribution µ(´) for different values of Prandtl number Pr when (a) S = 0:8 and (b) S = 1:2. 

Moreover, when 𝑆→0, the solution approaches to the analytical solution obtained by Crane⁷ with infinitely thick layer of fluid, i.e. (𝛽→∞). In addition, 𝑆→2 represents a liquid film of infinitesimal thickness (𝛽→0).

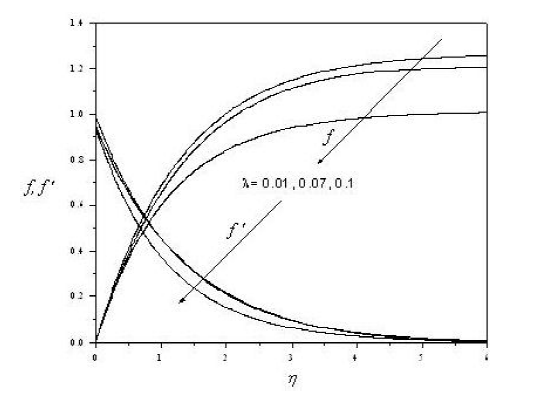
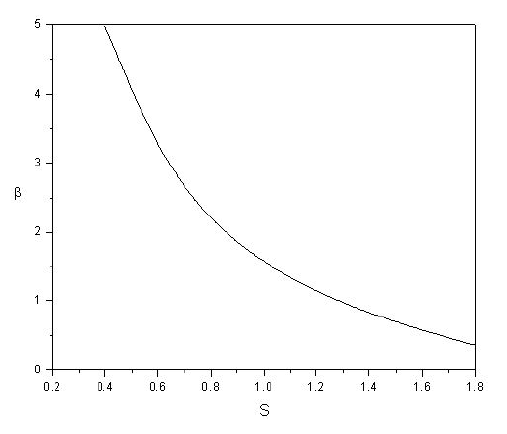
Figure 2 shows the effect of slip parameter, on horizontal as well as transient velocity profile. It is observed from this figure that horizontal velocity profile 𝑓′(𝜂) decreases with increase of slip parameter 𝜆, and the opposite trend is noticed for transient velocity profile 𝑓(𝜂). Further, Fig. 3 indicates the variation of film thickness 𝛽 with the unsteadiness parameter 𝑆. From this figure, it is noticed that 𝛽 monotonically decreases when 𝑆 increases, which matches with that reported by Wang and Abel et al.⁴³.

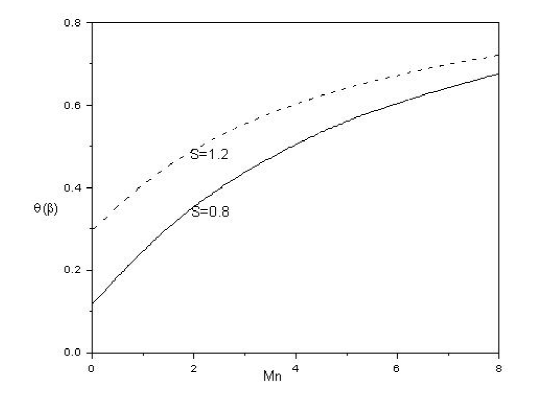
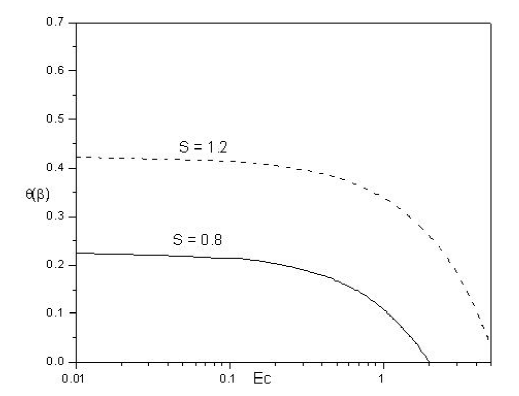
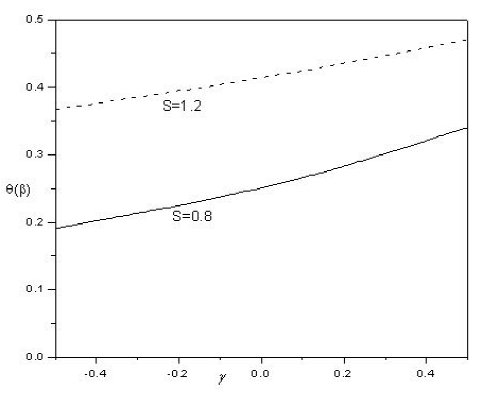
The effect of magnetic parameter 𝑀𝑛, Prandtl number 𝑃𝑟, Eckert number 𝐸𝑐 and heat source/sink parameter 𝛾 on the surface temperature $\theta {\left}(\beta {\right})$ are illustrated from Figs. 4 to 7, respectively. Clearly, increasing values of magnetic parameter 𝑀𝑛 causes the surface temperature to blow-up monotonically. Further, small values of Eckert number 𝐸𝑐 almost keep the surface temperature a constant, but enhance the surface

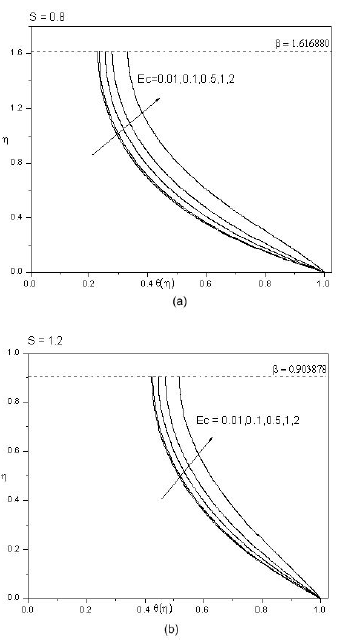
Figure 10 Variation of the temperature distribution µ(´) for different values of Eckert number Ec when (a) S = 0:8 and (b) S = 1:2. 

temperature for higher values. However, the opposite effect is exhibited in case of 𝑃𝑟 i.e., increasing values of 𝑃𝑟 decreases the surface temperature. For Prandtl number of order unity and below the surface temperature 𝜃(𝛽) attains a finite value below 1 and the temperature gradients extend all the way to the free surface. In the limiting case 𝑃𝑟→0, however, the dimensionless surface temperature tends to unity i.e. the temperature 𝑇 becomes uniform in the vertical direction and equals 𝑇 𝑠 . This is consistent with the trivial solution 𝜃(𝜂)=1 obtained from the thermal energy Eq.([eq:15]) when 𝑃𝑟=0. Moreover, at sufficiently high Prandtl number, i.e. low thermal diffusivity, the surface temperature remained practically equal to zero. The dimensionless heat/sink parameter (𝛾<0) is to reduce the temperature distribution significantly throughout the region as (𝛾>0) brings about the temperature increase throughout the entire region. These observed results hold good for different values of unsteadiness parameter 𝑆.

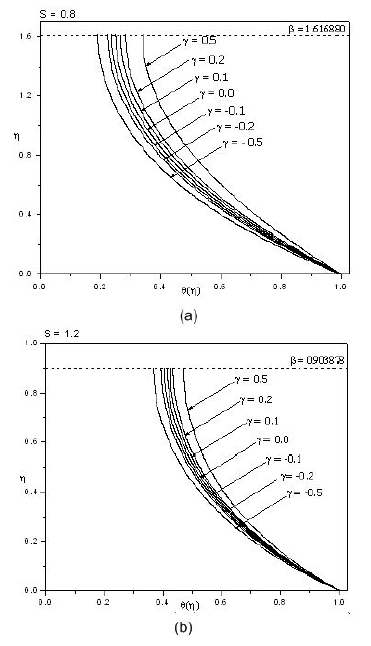
Figure 11 Variation of the temperature distribution µ(´) for different values of the dimensionless heat/sink parameter ° when (a) S = 0:8 and (b) S = 1:2. 

The effect of magnetic parameter 𝑀𝑛 on the horizontal velocity profiles are depicted in Figs. 8(a) and 8(b) for ??=0.8 and 𝑆=1.2, respectively. From these plots, one can make out that the increasing values of magnetic parameter decreases the horizontal velocity. This is expected as the applied transverse magnetic field produces a drag in the form of Lorentz force thereby decreasing the velocity magnitude. Dropping in horizontal velocity is a consequence of increase in the magnetic field strength as observed for 𝑆=0.8 as well as 𝑆=1.2.

Figures 9(a) and 9(b) demonstrate the effect of Prandtl number 𝑃𝑟 on temperature profiles for two different values of unsteadiness parameter 𝑆. These plots reveal the fact that for a particular value of 𝑃𝑟, the temperature increases monotonically from the free surface temperature 𝑇 𝑠 to wall velocity 𝑇 0 , which concurs with the results of Anderson et al. . The thermal boundary layer thickness decreases drastically

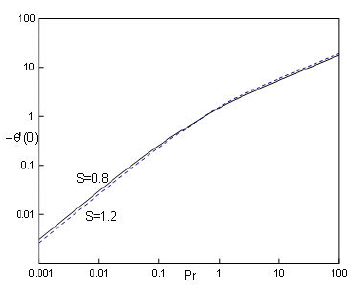
Figure 12 Temperature gradient ¡µ0(0) at the sheet as a function of Prandtl number Pr for S = 0:8 (the solid curve) and S = 1:2 (the dotted curve). 

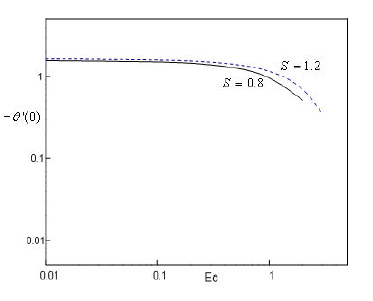
Figure 13 Temperature gradient ¡µ0(0) at the sheet as a function of Eckert number Ec for S = 0:8 (the solid curve) and S = 1:2 (the dotted curve). 

for high values of 𝑃𝑟 i.e., low thermal diffusivity. From these figures, we observe that Prandtl number 𝑃𝑟 speeds up the cooling of the thin film.

The effect of Eckert number 𝐸𝑐 on temperature profiles for two different values of unsteadiness parameter 𝑆 are projected in Figs. 10(a) and 10(b). The effect of viscous dissipation is to enhance the temperature in the fluid film. i.e., increasing values of 𝐸𝑐 contributes in thickening of thermal boundary layer. For effective cooling of the sheet a fluid of low viscosity is preferable.

Figures 11(a) and 11(b) present the effect of dimensionless heat source/sink parameter 𝛾 on temperature profile for different values of unsteadiness parameter 𝑆. In addition, for 𝛾<0, there is reduction of temperature in the thermal boundary layer region, where as opposite trend is noticed for 𝛾>0.

Table III tabulates the values of surface temperature for various values of 𝑀𝑛, 𝑃𝑟, 𝐸𝑐 and 𝛾. This table reveals that 𝑀𝑛 proportionately increases the surface temperature, whereas 𝑃𝑟 and 𝐸𝑐 decreases the surface temperature.

The dimensionless wall temperature gradient −𝜃′(0) takes a higher value at a large Prandtl number 𝑃𝑟. The effect of −𝜃′(0) for 𝑆=1.2 only marginally exceeds that for ??=0.8 when 𝑃𝑟>1 (see Fig. 12). The dimensionless wall temperature gradient −𝜃′(0) takes a uniform value at certain moderate values of Eckert number 𝐸𝑐, while the effect of −𝜃′(0) decreases with increasing 𝐸𝑐 (see Fig. 13).

5. Conclusions

In the presence of the velocity slip, this analysis provides solutions for unsteady viscous incompressible boundary layer flow of a fluid film over a heated stretching surface in the presence of a variable transverse magnetic field including the viscous dissipation and internal heating effect. The current results reveal that magnetic field and viscous dissipative effects play a significant role on controlling the heat transfer from stretching sheet to the liquid film. The important findings pertaining to the present analysis can be epitomized as follows:

The transverse magnetic field suppress the velocity field which causes enhancement of the temperature profiles.

The viscous dissipation effect is characterized by Eckert number 𝐸𝑐. Comparing to the results without viscous dissipation, it is seen that the temperature increases, when the fluid is being heated (𝐸𝑐>0) but decrease when the fluid is being cooled (𝐸𝑐<0). This result reveals the effect of viscous dissipation and enhances temperature in the thermal boundary layer region.

For a wide range of 𝑃𝑟, the effect of viscous dissipation was found to increase the dimensionless free surface temperature 𝜃(1) for the fluid cooling case. The impact of viscous dissipation on 𝜃(1) diminishes in the two limiting cases: 𝑃𝑟→0 and 𝑃𝑟→∞, in such situations 𝜃(1) approaches unity and zero respectively.

The effect of internal heat source/sink is to generate temperature for increasing positive values and absorb temperature for decreasing negative values. However, negative value of this parameter is better suited for cooling purpose.