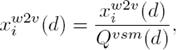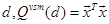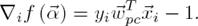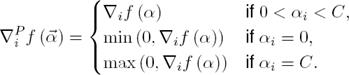1 Introduction
In machine learning (ML) platforms the current front-line of “Big Data” deals with millions of training and test documents as well as hundreds of thousands, or even millions of labels. Therefore, scalable learning and optimization in the deep architecture are the key to deal with such large-scale date-sets. Although strong ML methods such as Support Vector Machines (SVMs) [2, 4, 20] have been successfully applied to text classification (TC).
In general, ML-based TC can be categorized into two classification tasks: a flat classification (FC) [5, 13, 14, 17] by referring to standard binary or multi-class classification problems where parent-child relations are completely omitted. Second is the hierarchical classification (HC) [15, 16] – typically a tree, a directed acyclic graph (DAG), or a directed graph (DG) are incorporated, where the classes to be predicted are organized into a class hierarchy. A very large amount of research in TC, data mining (DM), and related researches have focused on FC problems. In contrast, many important real-world classification problems are naturally cast as HC problems. In Big Data platform, the size of data is too large to implement suitable classifiers. Moreover, it is difficult to label new data into predefined categories since text and labels are growing exponentially. Therefore, it is still an open and more challenging problem to design and implement such a model that classify large-scale documents into large-scale hierarchically-structured categories accurately and efficiently.
To generate text to vector, statistical vector space model (VSM) is a common fashion for learning and prediction tasks. But in complex hierarchical domain where many categories require extremely large training sets to achieve higher accuracy. To build efficient scalable learning model where a mini-batch is considered by random sampling from large training sets of a certain node. In the prediction stage, many or completely missing features are appeared in vector space model (VSM) because of sparsity, that can not precisely predict the leaf categories for a candidate sample.
Here, semantic learning based on unsupervised technique to learn continuous feature representations may give a shed to predict the candidate samples. In the above directions, this paper presents edge representations learning (edge2vec) where each edge in the hierarchy a statistical feature vector and a semantic feature vector based on word and paragraph representations from unlabeled data are incorporated. In edge2vec, we first learn word representations based on word-word co-occurrence from unlabeled data to generate word vectors.
We then infuse continuous weights into features along with discrete weights in the VSM. In addition, We then learn paragraph vectors and infuse continuous weights of paragraph vectors into features. The new input vector for deep or hierarchical learning, we call hierarchical semantically augmented statistical vector space model (hSAS-VSM). This study makes the following major contributions with introducing the edge2vec based hSAS-VSM approach to address large-scale classification task:
— The proposed edge representations learning (edge2vec) consists of discrete and continuous feature learning using word vectors (word2vec) and paragraph vectors (para2vec).
— The hSAS-VSM enriches the existing statistical-VSM using semantic knowledge for words and documents.
— The proposed edge2vec follows the inductive learning and deductive classification for very large-scale dataset. The training and test speed for learning and classification are fast which makes the system scalable.
— Infusing embedding features are useful to enrich the categorical performance for large-scale dataset.
— We introduce a balanced stochastic dual coordinate ascent for linear support vector machines for efficient learning and to adjust the positive-negative samples imbalance in a certain node in the hierarchy.
— The proposed edge-based learning is not only reduce the computational cost but also can significantly improve the classification score. Therefore, edge-based learning is a prominent approach for hierarchical classification.
2 Related Work
TC is a typical multi-class single- and multi-label classification problem. Platt [11] proposed a faster training of SVM using sequential minimal optimization (SMO) that breaking a very large quadratic programming optimization problem into a series of smallest possible problems as an inner loop in each outer iteration. The approach is generally 1200 and 15 times faster for linear and non-linear SVMs respectively.
Studies to solve multi-class multi-label classification have been summarized in [18], in three smaller data sets with maximum labels of 27 in compare to current front-line of multi-label classification task. Sohrab [14, 16] proposed a semantically augmented statistical vector space model (SAS-VSM) by introducing word embedding into feature for single- and multi-label text classification (TC). In this work, the SAS-VSM is introduced in FC and outperformed in compare to VSM. There have been many studies that use local context in HTC [1, 7, 10]. Chakrabarti et al. [1] proposed a Naive-Bayes document classification system that follows hierarchy edges from the root node. Koller et al. [7] applied Bayesian networks to a hierarchical document classification. In LSHTC3, the arthur system [21] successfully applied meta-classifiers to the large-scale hierarchical text classification (LSHTC) task.
Meta-classifiers can also be regarded as a sort of pruning. The system employed Liblinear, Max Entropy classifier, and SVMlight. The meta-classifier with SVMlight achieved 43.81% on the aspect of accuracy; however relatively slow in compare to Liblinear and Max Entropy on the aspect of efficiency. Lee [8] proposed a Multi-Stage Rocchio classification (MSRC) based on similarity between test documents and label’s centroids for large-scale datasets.
The system used greedy search algorithm in the predicted label set and then compare similarities between test documents and two centroid to check whether more labels are needed or not. The MSRC achieved 39.74%, 43.26%, and 67.83% in terms of accuracy, LBMiF, and HF respectively for Wikipedia medium dataset. On the aspect of efficiency the system is much faster than baseline such as K-Nearest Neighbor when the expected number of labels per document are less.
3 Our Approach: Edge Representations Learning
Edge representations learning (edge2vec) is formulated with different words or terms and document representations in natural language processing (NLP). It consists of discrete and continuous feature learning from words and documents using word and paragraph vectors respectively. Consider a hierarchy H (N, E), where N is the set of nodes and E is the set of edges. A hierarchy H is a collection of superiors or parents and subordinates or children categories. In edge2vec, a certain edge ei in the hierarchy H is augmented by hSAS-VSM. Each edge ei is an edge2vec optimized-based learning model by propagating a set of samples associated with a certain node ni. The SAS-VSM is the inspiration which leads to generate edge2vec for a certain edge in the hierarchy by infusing paragraph vectors along with word vectors into features for hSAS-VSM.
The sample augmentation process of edge2vec consist of three sub-tasks. First is the VSM-based edge2vec learning i.e. edge2vecvsm, second is the hSAS-VSM-based learning using word vectors i.e. edge2vecvsm,w2v. Finally we generate edge2vecvsm,w2v,p2v which incorporated with VSM, word and paragraph vectors in the sample augmentation process.
3.1 Hierarchical SAS-VSM: hSAS-VSM
Our approach for learning word vectors into features along with existing supervised VSM is inspired by SAS-VSM. The inspiration is that how to infuse continuous word and paragraph vectors along with discrete weights into features for hSAS-VSM in very large-scale extreme multi-label HTC. In the hSAS-VSM, an augmented document space D = {d1, d2, ...dn} can be denoted as:
 where
where  is a hSAS-VSM augmented feature vector for a document
is a hSAS-VSM augmented feature vector for a document 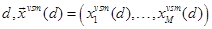 is a statistical feature vector can be defined as:
is a statistical feature vector can be defined as:
where f(ti) is a term weighting function
representing any weighting approach for term ti. To
avoid excessive effects of large feature values in the  , we normalize the weight
for document d as:
, we normalize the weight
for document d as:  .
. 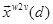 and
and  are semantically augmented
feature vectors using word and paragraph vectors respectively.
are semantically augmented
feature vectors using word and paragraph vectors respectively.
3.1.1 Word Vector in h SAS-VSM
For fast and accurate learning in deep architecture, first we introduce a simple solution
for infusing word vectors into features in large-scale hierarchical text
classification (LSHTC). Suppose that there are M words in matrix V and each
word is mapped to p-dimensions, then to compute
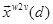 based on
word vectors as:
based on
word vectors as:
Word embedding vector V is defined as:
Each row  represents the word embedding vector for word or term ti. The new generated augmented features for document d are incorporated with discrete and continuous weights that get a larger weight than existing normalized statistical vectors. We therefore scale the
represents the word embedding vector for word or term ti. The new generated augmented features for document d are incorporated with discrete and continuous weights that get a larger weight than existing normalized statistical vectors. We therefore scale the 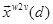 as:
as:
3.1.2 Paragraph Vector in h SAS-VSM
In TC, document D consists of a sequence of documents
{d1, d2,
...dn} in the corpus. In paragraph or
document vectors, matrix 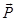 is an
N × q matrix with N
documents and each document is mapped to q-dimensions
continuous-valued vector. In (4), we can then generate the paragraph
vector-based
is an
N × q matrix with N
documents and each document is mapped to q-dimensions
continuous-valued vector. In (4), we can then generate the paragraph
vector-based  for a certain document d as,
for a certain document d as,
Paragraph vector P is defined as,
Each row  denotes the
embedding vector for document di. In the
edge2vec process, two properties are
of main concern: inductive learning and deductive classification.
denotes the
embedding vector for document di. In the
edge2vec process, two properties are
of main concern: inductive learning and deductive classification.
3.2 edge2vec in Inductive Learning
The inductive learning induces a set of observed instances or samples from specific bottom categories to general top categories in the category hierarchy. During inductive learning, the edge2vec follows the sample augmentation using hSAS-VSM. We then perform the bottom-up propagation a sampling strategy that assign all the augmented samples from a specific or leaf category to more general top category in the hierarchy. Finally, we train each edge in the hierarchy based on top-down walks.
3.2.1 Bottom-up Propagation
Since only leaf categories are assigned to data, first we propagate training samples from the leaf level to the root in the category hierarchy. Fig. 1a illustrates toy example of document propagation in a hierarchy consisting of ten categories R-I. In this figure, sample x1 is assigned to category F, x2 to F and G, x3 to H, x4 and x5 to I. Let us look at the case of x2 assigned to G. x2 of G is propagated to both categories C and D. Then, x2 of C is propagated to A and then to R. When x2 is propagated from D to A afterwards, to avoid redundant propagation, the propagation of x2 (originally from G via D) terminates at A, even if A is a parent category. We employ a recursive algorithm to perform the bottom-up propagation of the samples.
3.2.2 Edge-based Learning: Top-down Walks
Based on the propagation of training samples, we train the classifiers for each edge in the
hierarchy where each edge is coupled with a binary class classifier using
the one-against-the-rest approach. In Fig.
1b at node C, during the bottom-up propagation where
x1 and x2 are
assigned. Since edge-based learning is in concern, therefore model WCF is
trained in the hierarchy as to classify x1 and
x2 to F; whereas model WCG
is trained as to classify x2 to G but not
x2 to F. In large-scale hierarchical
learning, each node is propagated with hundreds of thousands, or even
millions of samples, where positive-negative samples imbalance occur
repeatedly. For efficient learning and to adjust the effect of
positive-negative samples imbalance in a certain node in the hierarchy, we
present a balanced stochastic dual coordinate ascent for linear support
vector machines (BS-DCASVM) with L1-loss function. For randomly chosen
 ,
BS-DCASVM updates the weight vector as:
,
BS-DCASVM updates the weight vector as:
where 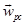 is a weight vector of
certain edge ei in the hierarchy. The
optimization process starts from an initial point α ∈
ℝl and generates a sequence of vectors
is a weight vector of
certain edge ei in the hierarchy. The
optimization process starts from an initial point α ∈
ℝl and generates a sequence of vectors 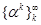 . We refer to the process
from αk to
αk+1 as an outer
iteration. In each outer iteration we have l inner
iterations, so that sequentially α1,
α2, ..., αl are
updated. Each outer iteration thus generates vectors
αk,i ∈ ℝ1. For updating
αk,i to
αk,i+1, must find the
optimal solution as:
. We refer to the process
from αk to
αk+1 as an outer
iteration. In each outer iteration we have l inner
iterations, so that sequentially α1,
α2, ..., αl are
updated. Each outer iteration thus generates vectors
αk,i ∈ ℝ1. For updating
αk,i to
αk,i+1, must find the
optimal solution as:
where C > 0 is a regularization parameter. ∇if is the ith component of the gradient ∇if. To evaluate ∇if(αk,i):
In (6), we move to index i + 1 with updating 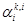 , if and only if the
projected gradient
, if and only if the
projected gradient 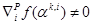 and satisfy the
following conditions:
and satisfy the
following conditions:
In (5),  is the current value and αi is the value after the updating. In the inner iterations of a certain node, in each iteration we maintain the updates of a weight vector
is the current value and αi is the value after the updating. In the inner iterations of a certain node, in each iteration we maintain the updates of a weight vector 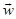 in a balanced stochastic way, by randomly chosen one from positive samples
in a balanced stochastic way, by randomly chosen one from positive samples  and in next iteration the other from negative samples
and in next iteration the other from negative samples  .
.
3.3 edge2vec in Deductive Classification
The deductive classification deduces a set of unlabeled samples from general top categories to more specific bottom categories in the hierarchy. In deductive classification, edge2vec follows the unlabeled samples augmentation as stated in 2.1, decision-based top-down walks for classification with global adjustments, and global pruning.
3.3.1 Global Decision-based Top-down Walks
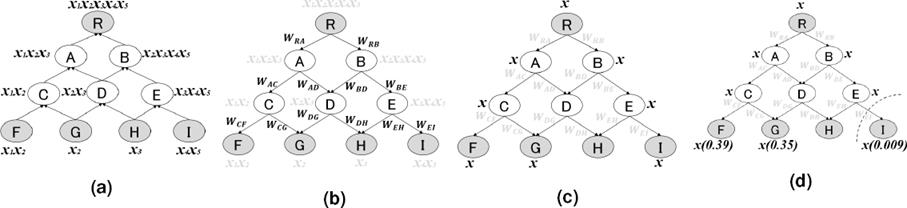
Fig. 1c illustrates top-down classification of test data  . First,
. First,  is classified to A and B, based on the decision by
is classified to A and B, based on the decision by 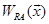 and
and 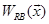 , respectively. The decision is made by:
, respectively. The decision is made by:
To adjust the effect of positive-negative samples imbalance, we set a bias
β. When 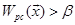 ,
,  is classified from
parent category p to child category c.
When both
is classified from
parent category p to child category c.
When both  and
and 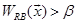 are
satisfied,
are
satisfied,  is classified into both A and B. Note that the standard bias term
bpc is automatically tuned for each edge
in the training stage. After the classification, we prune unlikely classes
for query sample x. We define a confidence score and set
the global threshold θ for it. When x
reaches a leaf node n, the confidence score
cα(x,
n) is calculated as follows:
is classified into both A and B. Note that the standard bias term
bpc is automatically tuned for each edge
in the training stage. After the classification, we prune unlikely classes
for query sample x. We define a confidence score and set
the global threshold θ for it. When x
reaches a leaf node n, the confidence score
cα(x,
n) is calculated as follows:
where E is a set of edges that x has followed in the path
from the root to the leaf n. The output value of a
classifier is converted to [0, 1] range by  . α is set to 2 from the
cross validation stage. When multiple nodes are assigned to
x, if c(x,
n) < θ, the assignment of
x to n is removed. Fig. 1d illustrates the global
pruning.
. α is set to 2 from the
cross validation stage. When multiple nodes are assigned to
x, if c(x,
n) < θ, the assignment of
x to n is removed. Fig. 1d illustrates the global
pruning.
4 Evaluation
In this section, we provide empirical evidence for the effectiveness of our proposed edge2vec in deep architecture. We employ official LSHTC evaluation metrics [19] and evaluate our systems on LSHTC evaluation site1 because the gold standard labels for the test data is not publicly available. Given documents D, correct labels Yi, and predicted labels Zi, the metrics are as follows:
— Accuracy(Acc):
1/|D|Σi∈D |Yi ∩ Zi|/ (|Yi ∪ Zi|).
— Example-based F1 measure (EBF):
1/|D|Σi∈D 2|Yi ∩ Zi|/ (|Yi| + |Zi|).
— Label-based Macro-average F1 (LBMaF):
Standard multi-label Macro-F1.
— Label-based Micro-average F1 (LBMiF):
Standard multi-label Micro-F1.
— Hierarchical F1 measure (HF):
The example-based F1-measure counting ancestors of true and predicted categories.
4.1 Base Algorithms
We employ sofia-ml2 for the experiments with Pagasos, SGD-SVM, Passive Aggressive (PA) [3], Relaxed Online Margin Algorithm (ROMMA) [9], and Logistic regression (logreg). The term frequency (TF), TF.IDF [13, 17], and TF.IDF.ICSδF [13, 17] are defined as:
where in (11)-(13), tf(ti, d)
is the number of occurrences of term ti in document d,
D denotes the total number of documents in the training
corpus, #ti is the number of documents in the
training corpus in which term ti occurs at least once,
D/#tii is the inverse
document frequency (IDF) of term ti,
C denotes the total number of predefined categories in the
training corpus, c(ti) is the
number of categories in the training corpus in which term
ti occurs at least once, and 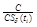 is the inverse class space
density frequency (ICSδF) of term ti.
Please refer to [13, 14] for more details.
is the inverse class space
density frequency (ICSδF) of term ti.
Please refer to [13, 14] for more details.
4.1.1 Word and Paragraph Vectors
In unsupervised learning, the statistics of word co-occurrences in a corpus is the primary source for learning word representations. The Word Vector (word2vec) [6] gives a shed on how meaning is generated and how the resulting word vectors might represent that meaning from the global corpus statistics. In this work, We consider the word2vec3 for learning word representations from unlabeled data to generate word vectors. We construct a matrix of word-word co-occurrences count from unlabeled corpora. We set a context window, and use a context ten words to the left and ten words to the right.
The unsupervised paragraph vector [12] is capable to learn continuous distributed vector representations of input sentences at any length: sentences, paragraphs, and documents. The paragraph vectors (para2vec) are generated from the available source code4. We run 25 iterations for all dimensional word and paragraph vectors. All parameters were left at default values in word2vec and para2vec.
4.2 Experimental Environments
We evaluate the edge2vec on standard multi-label HC for leaf nodes prediction through hidden or intermediate nodes in the hierarchy. We assess the training and classification time using a single Xeon 3.0GHz core with 396GB memory.
4.2.1 Dataset
To evaluate the performance of our proposed edge2vec, we compare our results with Wikipedia medium dataset (WMD) which considering as a benchmark for large-scale hierarchical classification.The WMD5 consists of 456,866 training documents with 346,299 distinct features and 81,262 test documents with 132,296 distinct features. It contains 36,504 leaf categories and 50,312 categories in the hierarchy with maximum depth 12. The number of edges in the hierarchy are 65,333. The category hierarchies of WMD is in the form of DAG.
We learn the word and paragraph vectors using 456,866 and 2,365,436 training documents from WMD and Wikipedia large dataset6 respectively. The vector representations of word and paragraph vectors are unsupervised learning that predicts the surrounding words in the paragraph. It is worth to mention that to learn paragraph vectors, a certain document is considered as one paragraph.
4.3 Experimental Results
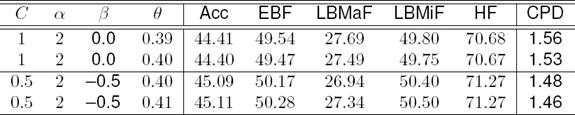
Table 1 shows the result with BS-DCASVM on flat vs hierarchical classification. For flat classification we achieve the best results in terms of accuracy while a set of parameters are set to C = 0.5, α = 2, β = −0.5, and θ = 0.70. In contrast, we achieve the best results while C = 0.5, α = 2, β = −0.5, and θ = 0.39 are set and the results show that the HC is outperformed in compare to FC.
Table 1 Flat (FC) vs Hierarchical Classification (HC) with BS-DCASVM

Note: CPD refers to categories per document
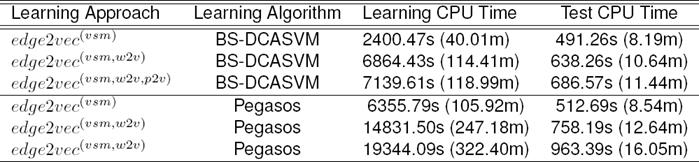
In Table 2, we compare the efficient learning algorithms of edge-based approach in the hierarchical architecture. From the results, we can see that edge-based system with the BS-DCASVM, Pegasos, and SGD-SVM are performing better in compare to PA, ROMMA, and logreg. Since BS-DCASVM is performing best among the learners and for space limitation therefore rest of the experiments are conducted with BS-DCASVM for infusing word and paragraph vectors into features. Table 3 shows the effect of different parameters and how it improves the performance.
Table 2 Comparison of efficient learning algorithms (LA)
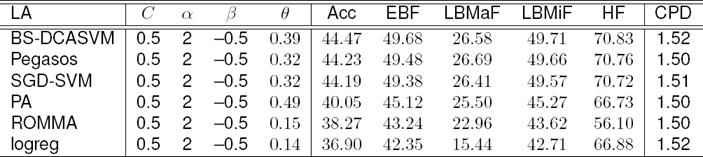
Note: CPD refers to categories per document
Table 4 shows how the added different dimensional embedding vectors (EV) allow edge2vec to achieve high performances. In this table, the edge2vec (word2vec, EV=100) denotes a document or sample is augmented by infusing 100 word vectors into features with existing statistical-VSM. The edge2vec (word2vec, para2vec, EV=100) represents a sample is augmented by infusing each 100 word and paragraph vectors into features incorporated with existing statistical-VSM.
Table 4 edge2vec with embedding vectors (EVs) over the BS-DCASVM
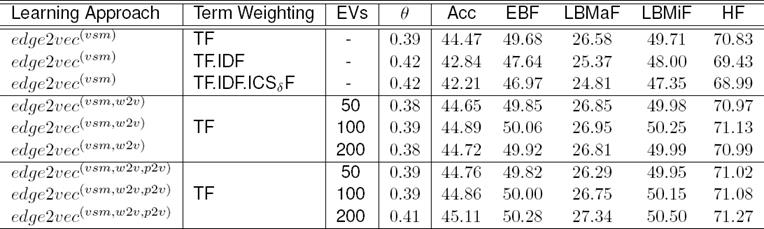
Note: In all cases, we use C = 0.5, α = 2, and β = −0.5
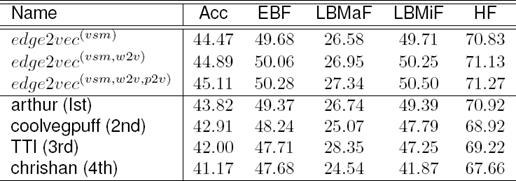
When β = −0.5 and θ = 0.41, we obtain the best performances 45.11%, 50.28%, 27.34%, 50.50% and 71.27% for Acc, EBF, LBMaF, LBMiF, and HF respectively. We summarize the results with compare to the top four systems participated in the LSHTC3 challenge in Table 5. Here edge2vec consistently outperforms the top system and achieves significant improvement over the other systems. We achieve a gain of 1.29%, 0.91%, 0.60%, 1.11%, and 0.35% for Acc, EBF, LBMaF, LBMiF, and HF respectively over the top system.
4.3.1 Parameter Sensitivity
The edge representations learning (edge2vec) involves a set of parameters in Table 3. We examine how different choices of parameters affect the performance of edge2vec over the WMD. We measure the Acc, EBF, LBMaF, LBMiF, and HF score as a function of parameters C, α, β, and θ.
The performance of edge2vec improves by changing the hyper-parameter C, β, and θ. We show the results with β ∈ (0.0, −0.5) and varied θ ∈ (0.38, 0.39, 0.40, 0.41). β = −0.5 allows the data classifies into negative side that means some incorrect assignments are kept for candidate sets. However, most of the incorrect classifications are removed afterward in the global pruning stage.
4.3.2 Scalability and Complexity
We learn edge2vec for 65,333 edges in the hierarchy. Table 6 shows the training and test efficiency with different learning algorithms of edge2vec approach. The total training time takes less than one hour including sample augmentation of 456,866 training samples, sampling, optimization, and writing 65,333 models. The optimization phase for a certain edge is made the learning more efficient using negative sampling.
For each outer iteration, we randomly select positive and negative samples in a balanced stochastic way from a mini-batch. Therefore learning in deep is compatible to handle any size of large-scale data efficiently and accurately. The normalize feature vectors are very effective in large-scale dataset by avoiding excessive effects of large feature value during learning and classification stage in the deep architecture.
In the test phase, global decision-based walks allow us to reach leaf categories efficiently. The total test time takes less than ten minutes for assigning 81,262 test data into 36,506 leaf categories through 50,312 intermediate or hidden categories using BS-DCASVM.
The complexity is to decide a category as the assignment for a query sample will be O(logn) with n leaf categories. Besides learning the best settings of parameter also reduce the additional training and test cost.
5 Discussion and Conclusion
We described edge representations that learns word and paragraph vectors for a certain edge to build a classification model. In edge2vec with additional optimized features help to improve the prediction task. The good performance demonstrates the merits of edge2vec in capturing the semantics of word and paragraph vectors. To achieve the best result in Table 1 for flat classification, where the threshold θ is set to 0.70. In multi-label classification, the higher threshold value of θ indicates many leaf categories are assigned for a candidate sample during the one-vs-rest approach which increase the computational cost.
It is noticeable that edge2vec-based HC is very efficient for learning and prediction tasks. It decreases the computational cost as well as increase the system performances. It is also noticeable that edge2vec outperformed top-group systems in LSHTC3, w.r.t the most of evaluation metrics. We believe that, to handle extreme multi-label LSHTC problems, the results will make an useful contribution as an useful performance reference.
Although this work focus on large-scale hierarchical classification task, but the edge representations approach can be applied to link prediction, opinion mining, sentiment analysis, or related works in deep architecture. Continuous feature representations are the key of many deep learning algorithms, it would be interesting how edge2vec can further contributes in deep learning workbenches. Our future work includes the development of much more efficient algorithms for large-scale datasets.











 nova página do texto(beta)
nova página do texto(beta)