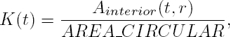1. Introducción
Innumerables problemas introducen grandes complejidades en el reconocimiento de objetos en imágenes digitales. Algunos de ellos, como las condiciones de iluminación, la posición y orientación de los objetos, el ruido y los datos espurios han sido abordados con mayor frecuencia en la literatura científica relacionada. Sin embargo, otros como la oclusión, no han sido tratados con la misma intensidad.
La oclusión en imágenes digitales puede ser clasificada teniendo en cuenta las causas que la provocan [5] en solapamiento, cuando un objeto oculta una porción de área de otro objeto que se quiere conocer; oclusión por opacidad, cuando la geometría del objeto oculta parte de sí mismo; y oclusión por sombra, provocada por el tipo de iluminación existente, ocultando el objeto (o parte de él) debido a su propia sombra o a la de otros objetos con los que este interactúa.
La oclusión constituye uno de los mayores obstáculos para alcanzar buenos resultados en las aplicaciones de reconocimiento de objetos. Aunque muchos autores han propuesto importantes soluciones a esta problemática [12, 8, 16, 5, 11, 13], la mayoría de ellas son muy dependientes del campo de acción donde se van aplicar, por lo que obedecen a condiciones muy específicas del entorno donde son utilizadas. Otras aproximaciones [6, 10, 1, 15] se ajustan a modelos matemáticos preestablecidos, los cuales no responden con eficacia a la heterogeneidad de los objetos que se pueden encontrar en muchas imágenes del mundo real.
Por todo lo anterior, en este trabajo se propone un método general para el reconocimiento de objetos ocluidos en imágenes digitales. El mismo aporta un nuevo enfoque del uso de los Modelos
Ocultos de Márkov en la segmentación de los objetos solapados. Para validar el método propuesto se realizaron experimentos con diferentes bases de datos, obteniéndose en todos los casos altos índices de efectividad. Los Modelos Ocultos de Márkov por su característica estocástica permiten que el método presentado en este trabajo posea una mayor flexibilidad y aplicabilidad que las investigaciones revisadas.
El trabajo se ha estructurado como sigue. Sección 1 es la introducción, en la sección 2 se presentan los trabajos revisados que contribuyeron al método propuesto. En la tercer sección se detallan los principales aspectos de la propuesta, se brindan los resultados y las comparaciones con las propuestas de la literatura en las que se sostiene la investigación. Y como último momento se dan las conclusiones y las principales ideas para trabajos futuros.
2. Trabajos relacionados
La tarea de reconocer un objeto cuando solo una parte de este es visible constituye, sin lugar a dudas, uno de los problemas más complejos en las aplicaciones de visión por computador. En la literatura especializada se pueden encontrar trabajos importantes que abordan la oclusión desde diferentes perspectivas.
Han y Jan [7] proponen un método de reconocimiento basado en el uso de puntos dominantes. Este enfoque sin lugar a dudas constituye un elemento importante para cualquier sistema de visión por computadora. Sin embargo, el análisis del reconocimiento de un objeto parcialmente ocluido utilizando solamente puntos dominantes puede resultar insuficiente para formar una representación íntegra de un objeto.
Liu y Srinath [10] proponen la representación de los objetos mediante polígonos. Esta aproximación presenta un comportamiento aceptable en objetos cuya forma responde curvas cercanas a los polígonos pero en contornos no regulares no es aplicable.
Bolles, Cain [1] y Tsang [15] combinan rasgos geométricos (líneas, arcos, esquinas), este método pese a que responde de manera correcta a figuras con contornos simples, dígase por simple que se acercan a algún modelo geométrico bien prestablecido, resulta insuficiente en objetos con formas irregulares que no responden a estos modelos.
Horácěk, Kamenický y Flusser [8] presentan un método para el reconocimiento de objetos parcialmente ocluidos de curvatura suave en imágenes binarias. Esta investigación propone dividir el objeto en partes mediante la detección de los puntos del contorno de cero curvatura. Cada parte del objeto se representa con un vector radial y se realiza el emparejamiento utilizando String Matching [2].
Mai, Chang y Hung [12] en su investigación dividen el contorno del objeto en segmentos delimitados por puntos que se obtienen como los máximos locales de construir el Espacio de Escala de Curvatura de la imagen (CSS Curvature Scale Space) y luego realizan el emparejamiento de los segmentos mediante el algoritmo de alineamiento de Smith-Waterman empleando como medida de similitud la correlación cruzada entre los vectores de rasgos de los segmentos.
Por su parte, Gonzáles [6] propone un método basado en la información de la forma para el procesamiento de solapamientos de eritrocitos. La división del solapamiento en varios objetos es realizada mediante la detección de los puntos cóncavos en el contorno y hallando la forma, circular o elongada, que más se ajusta al arco determinado por cada par de puntos cóncavos adyacentes, aplicando una serie de restricciones para determinar las circunferencias o elipses que se corresponden con cada célula dentro del agrupamiento.
3. Método propuesto
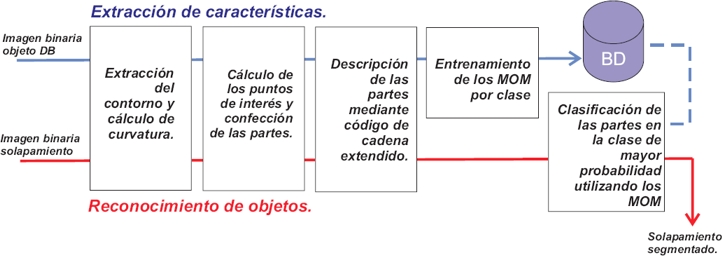
El método propuesto en este trabajo se centrará, según la clasificación de oclusión dada por [5], en los solapamientos, siguiendo una estrategia de reconocimiento de objetos mediante el análisis de la forma. El mismo se puede dividir dos etapas fundamentales: la extracción de características y el reconocimiento de objetos (ver Figura 1).
3.1. Extracción de características
La extracción de características parte de una imagen binaria, resultado de haber aplicado un método de segmentación a una imagen digital. En esta etapa se realizan los pasos descritos a continuación.
3.1.1. Extracción del contorno de la figura y cálculo de la curvatura del mismo
Una curva parametrizada puede ser entendida como la evolución de un punto que se mueve a lo largo del espacio 2D. Matemáticamente, la posición de un punto en el plano puede ser expresada como un vector p(t) = (X(t), Y (t)) donde t es un valor real llamado parámetro de la curva [3].
Sea una curva parametrizada p(t) se llamará curvatura tomando la propuesta realizada en [3] a la magnitud de la proporción entre el área interior al objeto y el área total en una vecindad circular para cada punto de la curva. En la Ecuación 1 se muestra como se realiza el cálculo.
donde Ainterior(t, r) es el área de intersección entre el objeto y el círculo de radio r fijado en el punto t del contorno y AREA_CIRCULAR es el área del circulo, la cual para un parámetro r es constante.
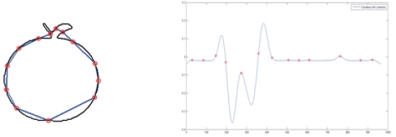
La curvatura es un concepto extremadamente importante porque expresa la naturaleza local geométrica de la curva. Por ejemplo un valor de cero para la curvatura corresponde a una línea recta, por otro lado si el valor es constante indica un círculo o un arco de círculo. De manera general la curvatura es proporcional a la variación local de la curva. Otro hecho importante de curvatura es que resulta invariante a rotaciones, traslaciones y reflexiones de la curva original. En este paso se extrae el contorno y se calcula la curvatura siguiendo la ecuación 1 del contorno mediante una proporción entre área interior al objeto y el área total en una vecindad circular para cada punto del contorno. En la figura 2 se muestra el gráfico de la curvatura para un objeto manzana.
3.1.2. Cálculo de los puntos de interés
La división del objeto en partes se realiza tomando como puntos de interés los elementos más cercanos a una cero curvatura entre dos extremos locales. Cada segmento del contorno delimitado por los puntos de interés constituirá una parte. Así un objeto estará formado por una secuencia de partes. En la figura 3 se muestran los puntos de interés detectados para un objeto manzana.
Los segmentos de contorno delimitados por estos puntos serán las partes que conformarán el objeto. Cada parte es parametrizada utilizando en código de cadena extendido [14].
3.1.3. Entrenamiento de los Modelos Ocultos de Márkov
Luego de obtener la representación de los objetos de entrenamiento, mediante la detección de puntos de interés y la parametrización de los segmentos de contorno con el código de cadena, se entrena un Modelo Oculto de Márkov (MOM) por clase, utilizando las posibles direcciones del código de cadena como observaciones y como cantidad de estados la media de la cantidad de partes de las clase.
Un MOM es un modelo estadístico en el que se asume que el sistema a modelar es un proceso de Márkov de parámetros desconocidos. El objetivo es determinar los parámetros desconocidos de dicha cadena a partir de los parámetros observables.
De manera general se define un MOM [4], como un modelo probabilístico, utilizado para representar la probabilidad conjunta de un conjunto de variables aleatorias. Estas variables aleatorias son de dos tipos; el primer grupo corresponde a los posibles símbolos observables Ot, que pueden presentarse al realizar una observación del sistema. El segundo corresponde al estado en el cual se encuentra el sistema oculto durante una observación Ot. Matemáticamente un MOM se puede definir como una tupla λ = {S, O, α, β, π} donde:
S es un conjuntos de estados S = {s1, s2, ..., sn}
O en el conjunto de observaciones O = {o1, o2, ..., om}
α es la matriz de probabilidades de transición de los estados si, α(i, j) = P [Xt+1 = sj|Xt = Si].
β es la matriz de probabilidades de probabilidades de emisión de los símbolos oi, β(i, k) = P [Ot = ek|Xt = Si].
π es el vector de probabilidades iniciales para los estados, π(i) = P [X1 = Si].
Existen tres problemas fundamentales al emplear un MOM, a saber:
Evaluación del modelo: Dada una secuencia de observaciones O = {o1, o2, ..., on} y un modelo λ , determinar P [O|λ]. Para dar solución a este problema comúnmente son utilizado los algoritmos Forward o Backward [4].
Decodificación: Dada una secuencia de observaciones O = {o1, o2, ..., on} y un modelo λ , encontrar la secuencia de estados ocultos 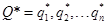 tal que:
tal que:
Su solución se obtiene mediante el algoritmo de Viterbi [4].
Aprendizaje: Dada una secuencia de observaciones O = {o1, o2, ..., on} determinar los parámetros del modelo. El algoritmo empleado tradicionalmente para su solución es el algoritmo Baum-Welch [4].
3.2. Reconocimiento de objetos
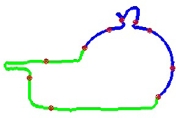
En esta etapa se realiza el reconocimiento de las partes de los objetos. Para ello se parte una imagen binaria de un solapamiento, en la figura 4 se muestra el contorno de un solapamiento. Se realiza, el proceso de extracción de características y se clasifica cada parte de un solapamiento en la clase de mayor probabilidad utilizando los MOM entrenados por clase.
La clasificación de las partes se realiza utilizando el algoritmo Forward-Backward. Una vez clasificada cada parte el objeto se segmenta mediante la unión de partes consecutivas, esto como una primera aproximación a solapamientos de grado dos (ver figura 5).
3.3. Resultados
Para la evaluación se utilizaron dos bases de datos de imágenes. La primera colección de objetos se creó de manera artificial y consistió en objetos geométricos básicos, dígase cuadrados, círculos y triángulos. Como segunda colección se empleó la base de datos de imágenes MPEG-7 Core Experiment CE-Shape-1 [9]. Esta cuenta con 70 clases, con 20 objetos por clase rotados y escalados. En la figura 6 se muestran algunos ejemplos de las clases.
La eficacia del método se comprobó mediante dos experimentos, evaluando el por ciento de partes bien reconocidas en los solapamientos formados artificialmente con objetos de las colecciones antes mencionadas.
3.3.1. Experimento 1
El primer experimento utilizó objetos de la primera base de datos por ser los más sencillos y por tener formas geométricas. Se tomaron 15 imágenes por cada clase para el entrenamiento y 5 para la validación. Los resultados fueron satisfactorios obteniendo el 94.63 % de las partes bien reconocidas. En la tabla 1 se muestra un resumen de estos, obtenidos luego de aplicarle el método a 100 solapamientos formados aleatoriamente con los objetos de la base de datos destinados para la prueba.
3.3.2. Experimento 2
En el segundo experimento se utilizaron objetos de la segunda base de datos. La configuración fue la misma que en el primer experimento con respecto a la división de la base de datos; 15 para el entrenamiento y 5 para la evaluación. Los resultados obtenidos en este caso disminuyeron a un 82.3 %. Este resultado se debe a que los objetos de esta base de datos poseen un nivel mayor en cuanto a complejidad de la forma.
Al igual que en el anterior experimento para esta prueba se generaron aleatoriamente 100 solapamientos con los objetos de la base de datos destinados a la evaluación. En la Tabla 2 se muestra un resumen de la efectividad de clasificación para algunos tipos de objetos.
Los trabajos presentados en [8] y [12] constituyeron antecedentes importantes para este trabajo. Los resultados presentados por ambos fueron los mejores encontrados en la revisión bibliográfica realizada a los métodos de reconocimiento de objetos parcialmente ocluídos. Cabe destacar que se encontraron otros métodos con mejores resultados pero en el reconocimiento de clases muy específicas de objetos dígase células, personas, etc. En la tabla 3 se muestra un comparación de estos dos métodos con la propuesta presentada en este trabajo.
Como se puede apreciar en la tabla 3 los métodos [8] y [12] obtienen resultados por debajo del método propuesto. Estos clasifican una sección visible de un objeto y no experimentan con contornos dónde aparezcan partes de más de un elemento de la base de datos, mientras que en esta propuesta si se tiene en cuenta que pueden aparecer partes de objetos diferentes en la sección visible del contorno (figura 7). Debido a esto al enfrentarse a contornos de figuras solapadas obtienen resultados inferiores a los de este trabajo.
Los trabajos [8] y [12] se comparan contra toda la base de datos de objetos empleando como medida de similitud una diferencia gaussiana y la correlación cruzada respectivamente. A diferencia de estos, la nueva propuesta presentada, responde a un esquema de clasificación supervisada por lo que para el reconocimiento no es necesario recorrer la base de datos.
4. Conclusiones y trabajo futuro
A partir del análisis de los trabajos estudiados y de la implementación de las propuestas realizadas en [8] y [12], en esta investigación se propone un nuevo método de reconocimiento de objetos solapados empleando los MOM. En la investigación se utilizan los MOM como una herramienta para el reconocimiento de objetos mediante el análisis de la forma en imágenes digitales.Se superaron los resultados de los métodos tomados como antecedentes de la investigación con un 94.63 % en un base de datos de objetos con formas geométricas simples y un 82.3 % en una base de datos de objetos con formas más complejas.
Como trabajo futuro se propone adecuar la propuesta para el reconocimiento de eritrocitos solapados en imágenes de muestras de sangre. Asimismo se desea experimentar con características de los objetos que tengan en cuenta el color y la textura.











 nova página do texto(beta)
nova página do texto(beta)