1. Introduction
Since the seminal work of Pecora and Carroll on synchronization 1, numerous works on chaos that comprises diverse areas such as lasers, chemical reactions, electronic circuits, biological systems, among others, have been studied. In particular, low-dimensional systems have been of interest in order to understand the synchronization and chaotic behavior in nature. The most studied and representative systems are the Lorenz, Chua, Rössler, van der Pol, Rayleigh, Duffing and their variations 2), (3), (4), (5), (6), (7.
The Rayleigh oscillator is much like the van der Pol oscillator. The Rayleigh and
Duffing oscillators are the paradigmatic circuits to study chaos in systems of
low-dimensional. The first gives a limit cycle and the last provides the prototype
of a strange attractor. It is well known, that a limit cycle is a closed trajectory
in phase space having the property that at least one other trajectory spirals into
it, when
Some applications of the Rayleigh and Duffing oscillators go from physics to biology, electronics, chemistry and many other fields. For instance, a possible application of synchronization in chaotic signals is to implement secure communication systems, since chaotic signals are usually broadband, noise like, and difficult to predict the behavior. They can also be used for masking information bearing waveforms 22) ,(23), (24. In robotics, the oscillators have been included to control joint hips and knees of human-like robots to ensure the mechanical system follows the right path. The generated signals can be used as reference trajectories for the feedback control 25), (26. Other application is in artificial intelligence. In fact, the oscillators have shown usefulness to training neuronal network and recognition of chaotic systems 27), (28.
As far as the coupling between the Rayleigh and Duffing oscillators is referred, we can mention three different couplings, namely: gyroscopic, dissipative and elastic 29), (30), (31), (32), (33), (34. Among the diverse way of coupling, the most used are the elastic and dissipative ones 34), (35), (36. In a previous work 34, it is analyzed a different approach of synchronizing two distinct oscillators of low-dimensional, using the aforementioned couplings. Uriostegui et. al37 studied synchronization between the van der Pol and Duffing oscillators by using the elastic, dissipative and a combination of both couplings. It was found that the elastic coupling leads to no synchronization, whilst with the dissipative one it is reached partial synchronization. For the combination of both couplings, it is reached complete synchronization.
In this work, we study and compare two types of couplings by using the Rayleigh and Duffing systems: the dissipative and the used previously by Uriostegui et. al34. It is important to remark that the studies in the literature on this kind of synchronization is based only on one coupling. An outline of this work is as follows. In Sec. 2, it is briefly studied the main features of the Rayleigh and Duffing oscillators. In Sec. 3, we study and compare two types of couplings using the Rayleigh and Duffing systems upon the master-slave configuration. In Sec. 4, some conclusions and an outlook are presented.
2. Dynamics of the oscillators
The dynamics of the forced Rayleigh oscillator is described by the following nonlinear differential equation:
The Rayleigh oscillator is characterized by nonlinear damping. The
as the Rayleigh potential, which represents a single-well (see Fig. 1 (a)). The potential has a minimum located at
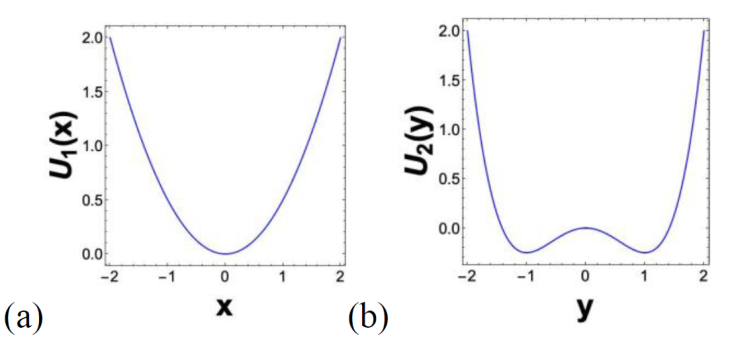
Figure 1 The potentials
We can observe from Eq. (3) that the
only fixed point is located at
On the other hand, the Duffing oscillator is a nonlinear dynamical system governed by
where
and
where we set
3. Master-slave synchronization
In this section, two different couplings for the Rayleigh and Duffing systems are studied and compared among themselves, namely: the dissipative and the one that combines elastic and dissipative couplings employed by Uriostegui et. al34. Let us stress that most of the research on synchronization is based on autonomous systems of three-dimensional or higher 38), (39), (40. Three of the most studied nonautonomous systems of low-dimensional with forcing are the Duffing, van der Pol, Rayleigh and their variations, since much of the dynamical features embedded in the physical systems can be realized on these systems 41), (42), (43. One important implication is that a two-dimensional continuous dynamical system cannot give rise to strange attractors. In particular, chaotic behavior arises only in continuous three-dimensional dynamical systems or higher. Most of the research on synchronization is based on autonomous systems that satisfy the Poincaré-Bendixson theorem. Nevertheless, let us stress that the Rayleigh and Duffing oscillators being two-dimensional, need an external forcing to present chaos.
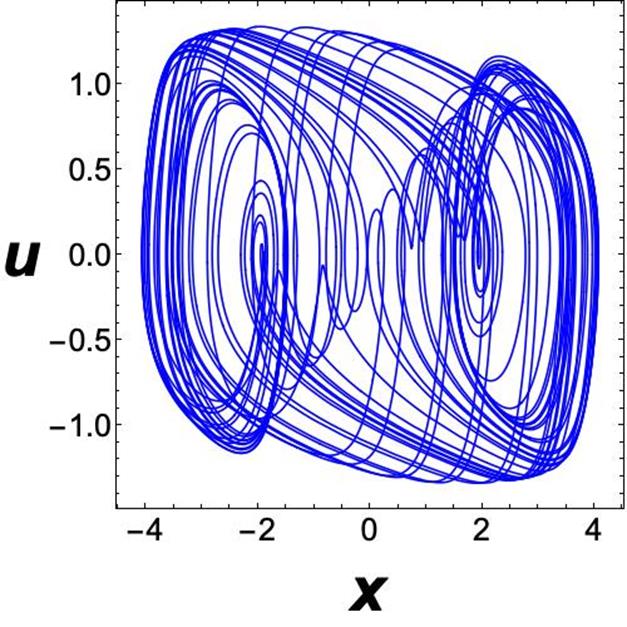
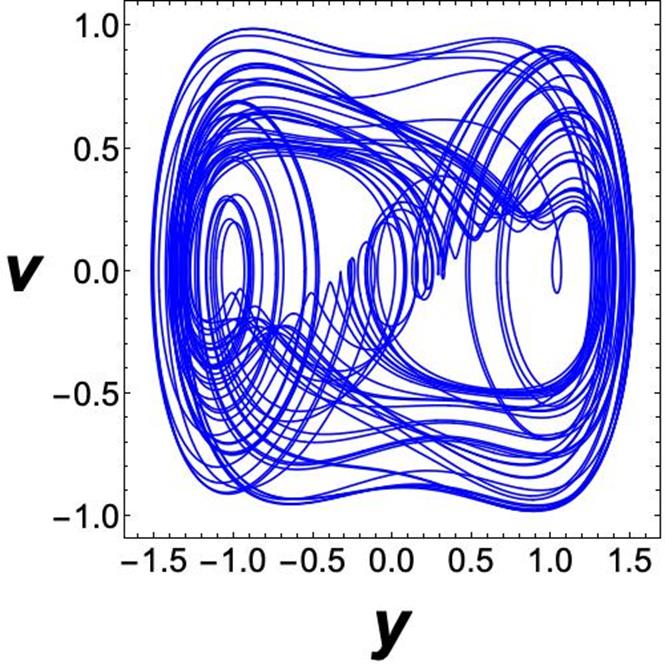
The dynamics for each oscillator under study is described by the equations in (1) and (4). The values of the parameters we use are as follows: (=1.2, α=0.3, ε=1, A1 =2.8, ω1 =0.2, A2 =0.5 and ω2 =1.3. In Figs. 2 and 3 it is displayed the respective trajectories with the initial conditions x (0) = 1, y (0) = 2, u (0) = 1 and v (0) = -1. Let us mention that the very same values of the parameters and the initial conditions will be used in the subsequent numerical simulations. The numerical simulations were performed using the fourth order of the Runge-Kutta method.
In the configuration master-slave, the Duffing oscillator acts as master and the Rayleigh oscillator as slave. For this case we have
In this instance, the coupling used corresponds to a dissipative coupling and it is
represented by
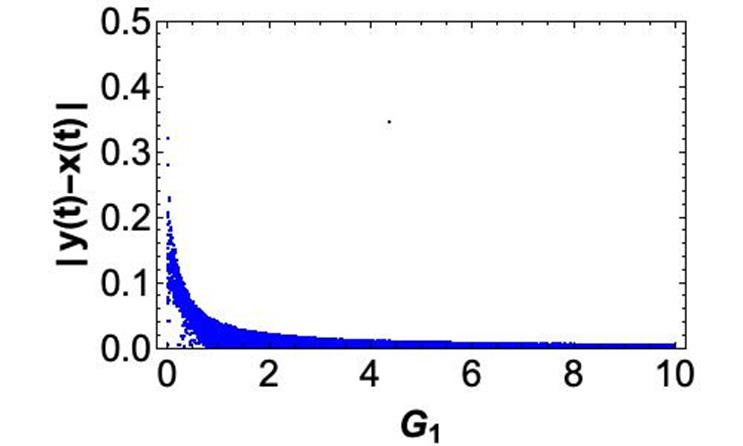
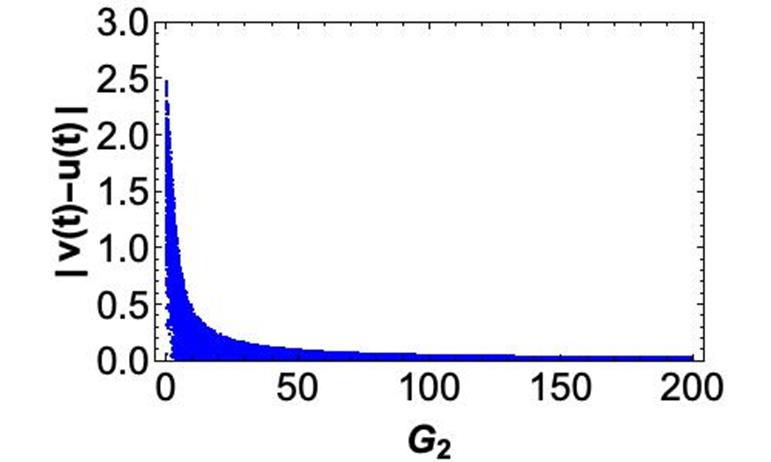
In general, the synchronization problem reduces to finding a suitable value of the
coupling strength
When the system is in practical synchronization, for a certain value of
for given positive values
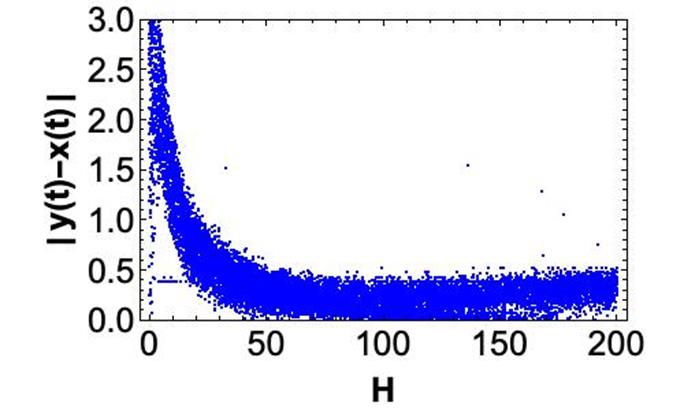
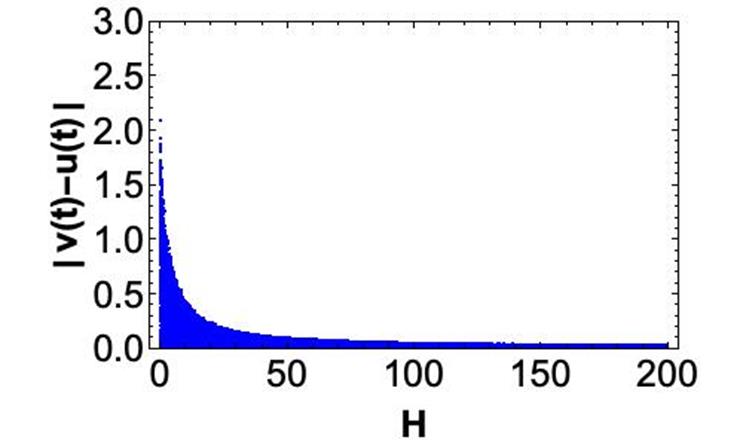
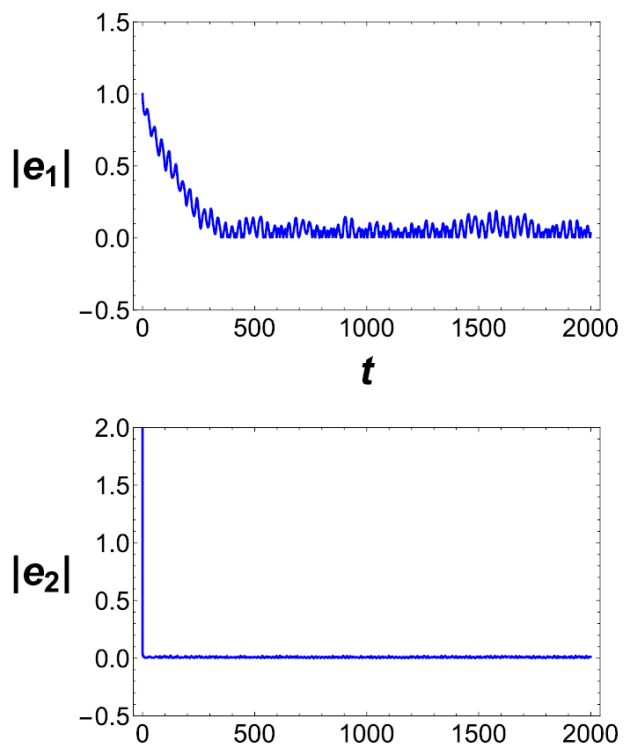
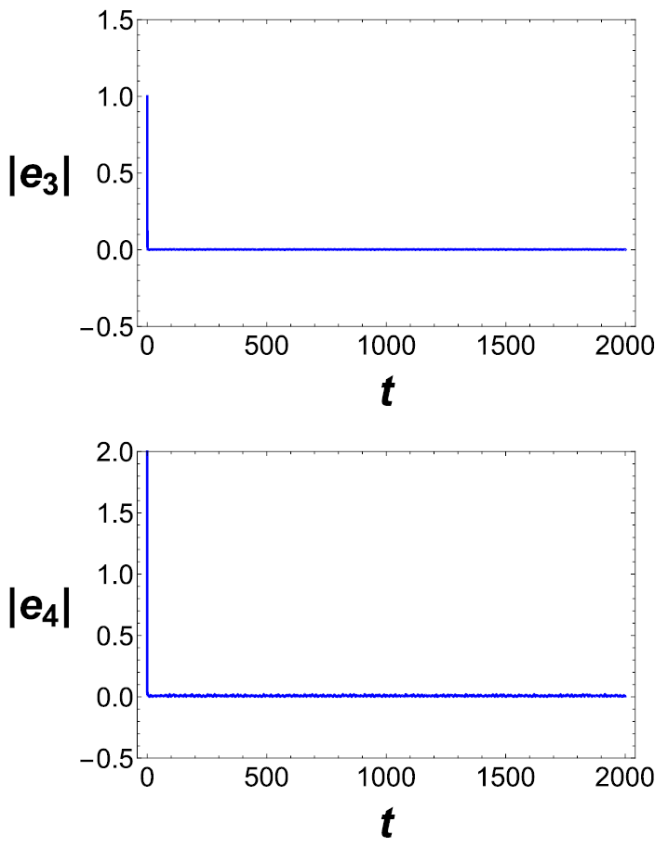
Let us consider the error functions
The plots of
In Figure 7, it can be appreciated from a
time-series plot of
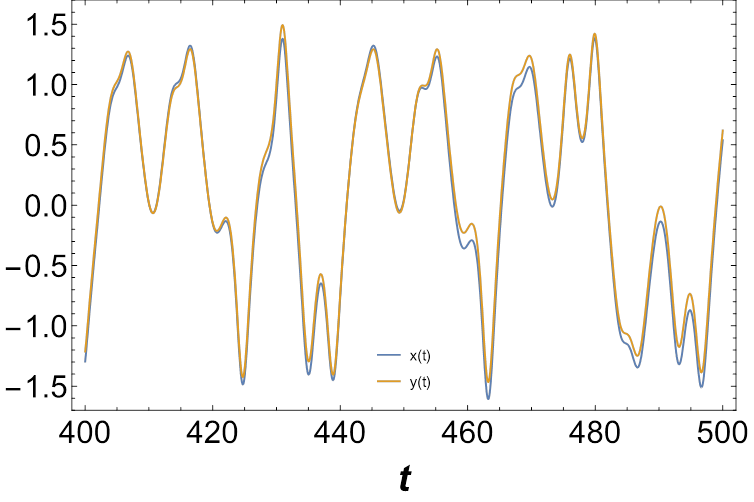
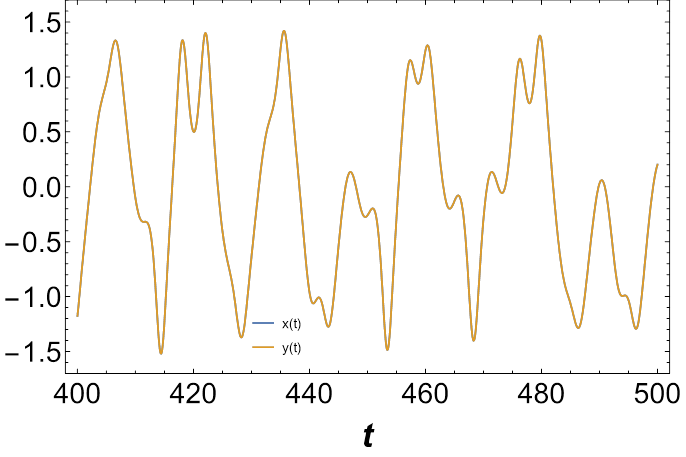
Let us analyze the projections onto the
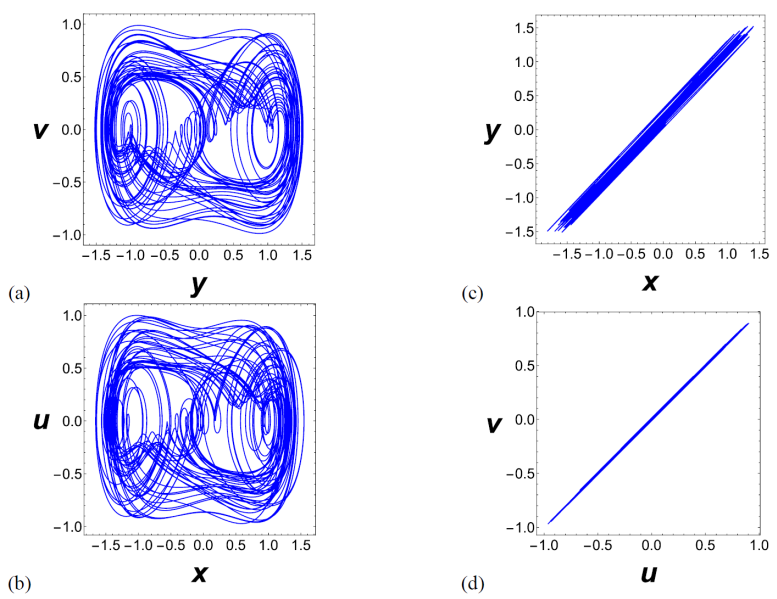
Figure 9 Dissipative coupling case, for
A modified master-slave scheme leading to synchronization even in the cases where the
classical master-slave scheme fails, was considered in Ref. 34. The system analyzed in this reference can be
separated in two parts (see Eqs. (13)
and (14)). On one side, the system
combines a non-conventional coupling, where linear feedback is made. The elastic
coupling is proportional to the difference of the position,
The errors
The constant
which is the called control vector, and it contains the coupling we propose. Notice
that the control depends on the error and its derivative. As before, for the case
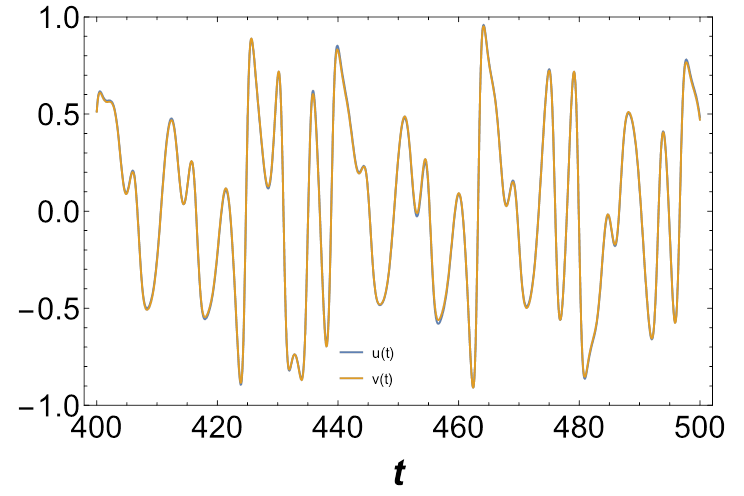
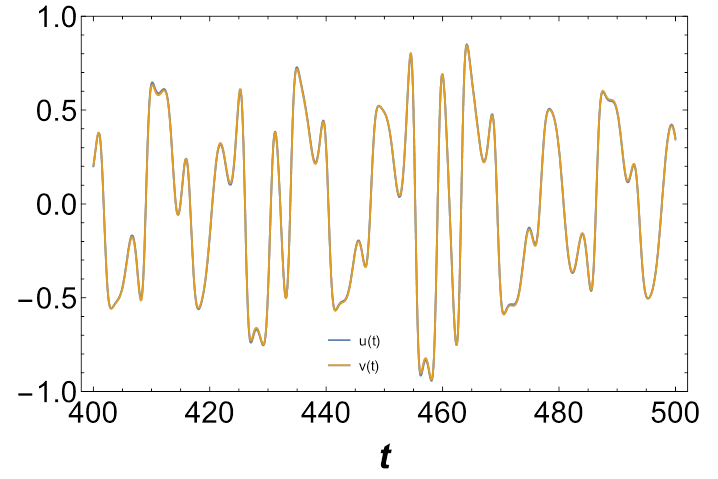
As it can be observed in Figs. 13 and 14, the time-series plots of
Let us now analyze the projections onto the
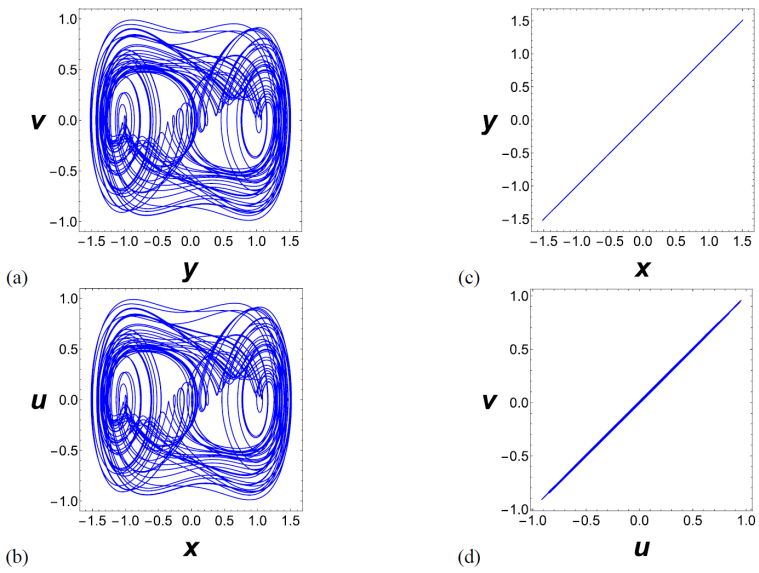
Figure 15 Elastic and dissipative couplings for
For certain systems, it is not possible to reach synchronization when the classical
master-slave scheme is used. In some cases, the systems reach complete
synchronization in a single state of the slave system as it occurs for the dynamics
contained in Eqs. (7) and (8), depending on
4. Conclusions
The Rayleigh and Duffing are low-dimensional nonautonomous systems that present chaos
and have been well studied. In this work, we have studied the master-slave
configuration in the Rayleigh and Duffing oscillators, when dissipative coupling is
used, only complete synchronization in the projection onto the











 nova página do texto(beta)
nova página do texto(beta)