Introducción
Uno de los objetivos fundamentales de las técnicas de estadísticas multivariantes es incrementar la capacidad explicativa de la comprobación empírica de la teoría, o bien, de incrementar el conocimiento teórico en los casos en que este sea escaso. Los modelos de ecuaciones estructurales son una técnica de análisis de datos multivariante de segunda generación que dan mayor nivel de confianza a la investigación por su eficiencia estadística mediante robustos y potentes softwares; su desarrollo ha supuesto una revolución en el campo de la investigación empírica, ya que permite examinar simultáneamente una serie de relaciones de dependencia entre variables independientes y dependientes. Estos modelos de ecuaciones estructurales pueden ser utilizados por investigadores de las ciencias sociales, ciencias de la educación, ciencias de la conducta, entre otros; a menudo son utilizados en la investigación de mercados, pues permiten probar teóricamente modelos causales (Haenlein y Kaplan, 2004; Statsoft, 2013).
Esta técnica estadística para series de estimaciones de ecuaciones simultáneas mediante regresiones múltiples se caracteriza por dos componentes básicos: 1) el modelo estructural y 2) el modelo de medida. El modelo estructural es el modelo guía que muestra las relaciones de dependencia entre variables independientes (exógenas) y variables dependientes (endógenas). El modelo de medida muestra las relaciones entre los constructos (variables latentes) y los indicadores (variables observables); en este modelo, el investigador puede evaluar la contribución de cada ítem (reactivo) a la escala de medición, es decir, especificar qué indicadores definen a cada constructo. Además, evalúa la fiabilidad de constructos e indicadores.
En la modelación de ecuaciones estructurales (SEM, por sus siglas en inglés) existen dos enfoques: el primero se basa en el análisis de estructuras de covarianza (CB, por sus siglas en inglés), el cual es recomendable cuando se contrastan teorías, pruebas de hipótesis o en el diseño de nuevas teorías, partiendo de la teoría y de investigaciones previas. El segundo es el enfoque de mínimos cuadrados parciales (PLS, por sus siglas en inglés) basado en el análisis de la varianza.
En el análisis de CB, y de acuerdo con las recomendaciones de Levy y Varela (2006), se tienen que considerar la teoría y las investigaciones previas, las cuales deberán ser el punto de partida de este tipo de modelos. En una situación real, la revisión de la literatura sobre el tema de investigación permitirá obtener un modelo teórico a partir del cual se especificará el dominio de los conceptos analizados y sus relaciones. También, la teoría permitirá la construcción de ítems referentes a los constructos (variables) y de dimensiones que se han establecido en modelos teóricos. Además, una característica fundamental de este enfoque es el cumplimiento con los supuestos estadísticos, como la normalidad de los datos y el tamaño de muestra, por lo que es considerado una técnica SEM paramétrica. Por lo anterior, Falk y Miller (1992) definieron a esta metodología como un sistema cerrado.
El segundo enfoque, referente al método PLS, se basa en el análisis de la varianza, lo que implica una metodología de modelación más flexible al no exigir supuestos paramétricos rigurosos, principalmente en la distribución de los datos. En este sentido, Wolf (1980) afirma que la modelación de ecuaciones estructurales con mínimos cuadrados parciales (PLS-SEM, por sus siglas en inglés) no requiere de las condiciones exigidas por la tradicional modelación de ecuaciones estructurales de covarianza (CB-SEM, por sus siglas en inglés) respecto a las distribuciones estadísticas (normalidad de los datos tamaño de la muestra en referencia a las variables observadas); es decir, utilizan pruebas no paramétricas. Los modelos PLS se utilizan bajo situaciones de predicción y no confirmatorias.
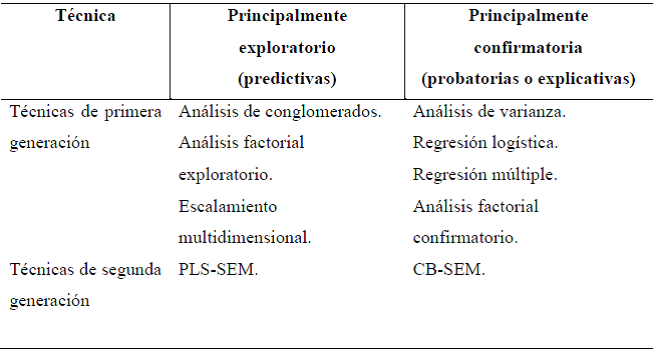
De manera concreta, Hair, Hult, Ringle y Sarstedt (2017, p. 2) clasifican los métodos multivariantes de primera y segunda generación como se muestra en la Tabla 1.
Con base en la clasificación anterior, el objetivo de este artículo científico es presentar una revisión documental sobre el método multivariante de segunda generación, SEM-PLS; se inicia con aspectos básicos metodológicos de la técnica y a través de datos ficticios se evalúa un modelo de investigación con la finalidad de que el lector pueda observar valores de los modelos de medida, del modelo estructural y de la evaluación global del modelo; en este caso se partió de una propuesta del modelo teórico a contrastar que contó con cinco hipótesis.
Aspectos clave en el uso de la PLS-SEM
La PLS-SEM emergió como una técnica para analizar las complejas relaciones entre variables latentes que permiten explicar los datos observados y el análisis predictivo como elemento relevante en la investigación científica.
El enfoque PLS fue desarrollado para reflejar las condiciones teóricas y empíricas de las ciencias sociales y del comportamiento. Los procedimientos matemáticos y estadísticos son rigurosos y robustos; pero el modelo matemático es flexible, en el sentido de que no establece premisas rigurosas en la distribución de los datos, en la escala de medición, ni en el tamaño de la muestra.
Para seleccionar el uso de la técnica PLS-SEM, Hair et al. (2017) parten de la premisa del objetivo de la investigación. Si el objetivo clave es la predicción de constructos, es recomendable hacer uso de esta técnica; por otra parte, si el objetivo es probar o confirmar una teoría, lo más recomendable es hacer uso de la CB-SEM. La PLS-SEM presenta exigencias menos restrictivas en la medición de escalas de tamaño de muestra y en la distribución de los datos. Es un enfoque que hoy en día ha adquirido gran aceptación, principalmente en los estudios de mercado y, en general, en las ciencias sociales.
Cabe señalar que la técnica de PLS puede ser usada tanto para la investigación explicativa (confirmatoria) como para la predictiva (exploratoria) (Henseler, Hubona y Ray, 2016; Hair et al., 2017).
De acuerdo con Shmueli y Koppius (2011), un modelo explicativo es un modelo construido con el propósito de comprobar las hipótesis causales que especifiquen cómo y por qué cierto fenómeno empírico ocurre. Un modelo predictivo hace referencia a la construcción y valoración de un modelo que pretende predecir nuevas o futuras observaciones o escenarios. El poder predictivo de un modelo se refiere a la capacidad del mismo para generar predicciones precisas de nuevas observaciones, ya sea en estudios transversales o longitudinales.
Construcción de un modelo sustentado en la teoría
La SEM parte de la justificación teórica que sustenta las relaciones de dependencia. La teoría puede definirse como un conjunto sistemático de relaciones que da una explicación exhaustiva de un fenómeno y permite al investigador distinguir qué variables predicen cada variable dependiente. La teoría es un objetivo prioritario de la investigación. Por lo tanto, la justificación teórica permite que el investigador reconozca que la SEM es un método confirmatorio, guiado más por la teoría que por los resultados empíricos; así, el investigador debe examinar cada relación propuesta desde una perspectiva teórica para asegurarse que los resultados sean conceptualmente válidos (Hair, Anderson, Tatham y Black, 2007). Por lo tanto, la SEM puede ser utilizado para probar los supuestos teóricos con datos empíricos (Haenlein y Kaplan, 2004).
Teoría de medición
La teoría de medición especifica cómo las variables (constructos) son medidas; esta metodología de la PLS-SEM presenta dos enfoques de medición. Un enfoque se refiere a la medición reflectiva y el otro a la medición formativa. De manera práctica, un modelo de investigación puede contener ambas (variables observables reflectivas y formativas). El que se incluya uno u otro o ambos dependerá del constructo a medir y del objetivo de la investigación.
Así mismo, la PLS-SEM al igual que el enfoque de covarianzas tiene varios índices que permitirán medir la relevancia y validez del modelo.
Medidas formativas versus medidas reflectivas
Las medidas formativas son constructos latentes compuestos por indicadores de medida, en el que los estos son causa o antecedente del constructo (Diamantopoulos y Winklhofer, 2001; Valdivieso, 2013). En el modelo formativo, cada indicador representa una dimensión del significado de la variable latente; eliminar un indicador significa que la variable pierde parte de su significado, de ahí la importancia de que los indicadores causen el constructo.
Respecto del modelo reflectivo, este se considera como un modelo de medida donde los indicadores de la variable latente son competitivos entre sí y representan manifestaciones de la variable latente. La relación causal va de la variable latente a los indicadores y un cambio en aquella será reflejado en todos sus indicadores. La diferencia entre los dos enfoques de medición está en la prioridad causal entre la variable latente y sus indicadores (Bollen, 1989).
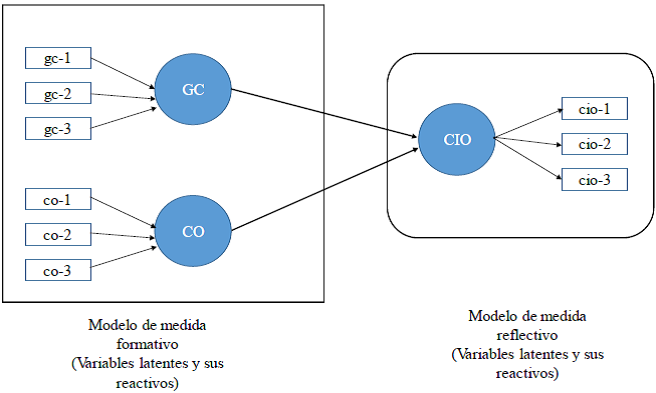
La Figura 1 muestra la diferencia entre las medidas formativas y las medidas reflectivas. Se puede hablar acerca de un modelo reflectivo cuando la variable latente es la causa de las medidas observadas (Simoteo, 2012).
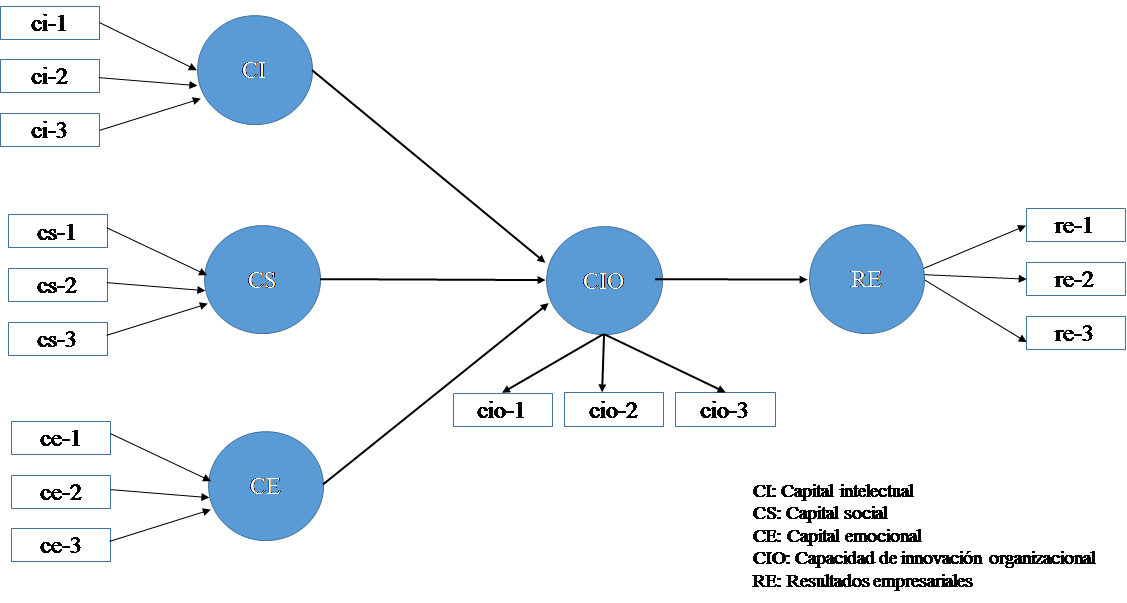
En la práctica, cuando se crea un modelo de trayectorias, como el que se muestra en la Figura 2, se observa también que el modelo contiene dos elementos. El primero, un modelo estructural que representa los constructos (elipses), cuya finalidad es desplegar las relaciones entre los mismos. El segundo, el modelo de medida, que muestra las relaciones entre los constructos y los indicadores (rectángulos). Es decir, los constructos (variables latentes) están representados por elipses y los indicadores (variables observables) por rectángulos. Los constructos y las flechas entre ellos hacen referencia al modelo interno o estructural, y los rectángulos y las fechas que causan el indicador o el constructo es el modelo de medida. Se observa que las variables latentes, en este caso denominadas CI, CS y CE, están representadas para su medición de manera formativa, mientas que las variables latentes CIO y RE están representadas para su medición de manera reflectiva.
Características de PLS-SEM
La PLS-SEM es una técnica de análisis multivariante cuya finalidad es probar modelos estructurales; aunque fue desarrollada desde hace varias décadas, se considera una técnica emergente. Esta metodología tiene como objetivo principal el análisis causal-predictivo en el cual los problemas analizados son complejos y el conocimiento teórico puede ser escaso (Lévy y Varela, 2006).
Hair et al. (2017) argumentan que la PLS-SEM presenta varias ventajas en comparación con otras técnicas SEM. Al ser una técnica más flexible, presenta las siguientes características: 1) esta técnica puede utilizar tamaños pequeños de muestra, aunque si esta es más grande aumenta la precisión, y no es necesario que se asuma una distribución normal de los datos (al ser la PLS-SEM un método no paramétrico, la escala de media recomendada es la ordinal medida en escala Likert1); 2) el número de ítems de cada constructo medido puede ser solo uno o bien puede conformarse por más de uno y en las relaciones entre constructos y sus indicadores se pueden incorporar métodos de medida reflectivos y formativos; 3) la PLS-SEM tiene como objetivo maximizar la cantidad de varianza explicada (maximiza el coeficiente de determinación [R2]); 4) en la evaluación del modelo global (estimación del modelo de medida) no se establecen criterios de bondad de ajuste, sino que se evalúan por separado las medidas reflectivas y formativas; 5) la evaluación estructural del modelo analiza los R2, la relevancia predictiva (Q2), el tamaño y la significancia de los coeficientes de regresión estandarizados o coeficientes path y los tamaños de los efectos (f2 y q2), y 6) el algoritmo básico de la PLS sigue un enfoque de dos pasos, el primero se refiere a la estimación iterativa de las puntuaciones de las variables latentes, y el paso segundo se refiere a la estimación final de los pesos, cargas y coeficientes path por medio de la estimación de mínimos cuadrados ordinarios (múltiples y sencillos) y en el análisis de componentes principales (Henseler, Ringle y Sarstedt, 2015).
De manera general, la PLS-SEM es un método estadístico no paramétrico. Aunque no requiere que los datos presenten una distribución normal, se requiere verificar que los datos no sean excesivamente no-normales, ya que, por lo general, este tipo de datos resultan problemáticos en la valoración de la significación de los parámetros. Es importante precisar que los valores de asimetría y curtosis2 mayores a uno son indicativos de valores altamente no normales.
Una de las características de la PLS-SEM es, precisamente, los tamaños pequeños de muestra; sin embargo, Marcoulides y Saunders (2006) sugieren que el tamaño mínimo de muestra dependa del número de relaciones que se especifiquen en el modelo (entre las variables latentes). Bajo esta perspectiva, en la Tabla 2 se observa el tamaño de muestra sugerido para este tipo de estudios.
Anteriormente, en la Figura 2, se pudo observar un modelo con cinco variables latentes y con cuatro relaciones entre las variables latentes (Capital Intelectual, Capital Social, Capital Afectivo, Capacidad de Innovación Organizacional y Resultados Empresariales); por lo tanto, de acuerdo con el criterio de Marcoulides y Saunders (Ibid.), el mínimo tamaño de muestra recomendado sería de 65 observaciones.
Desde el punto de vista de Kwong y Wong (2013), la PLS-SEM es conocida por su capacidad para manejar tamaños pequeños de muestra; esto no significa que el objetivo sea cumplir el requisito mínimo de tamaño de muestra. Hoyle (1995) recomienda un tamaño de muestra de 100 a 200 para potencializar los resultados del modelo, ya que al menos 100 observaciones pueden ser suficientes para alcanzar niveles aceptables de poder estadístico, dada una cierta calidad en el modelo de medida (Reinartz, Haenlein y Henseler, 2009). Por lo tanto, se sugiere apegarnos al tamaño de muestra mínimo de muestra de 100, siguiendo a Hoyle y con el fin de dar robustez a los resultados (Felipe, Roldan y Leal, 2017; Hernández, 2017; Barba y Atienza, 2017; Hernández et al., 2016).
Esta metodología estima en el mismo proceso las medidas del modelo de medida y del modelo estructural. Anderson y Gerbing (1988) sugieren que los resultados sean interpretados en dos sentidos: primero, evaluando las escalas de medidas o modelos de medida (reflectiva y formativa) y, segundo, evaluando el modelo estructural. Esta distinción es importante porque los procedimientos de validación son diferentes (Dimantopoulus, Riefler y Roth, 2008; Kwong y Wong, 2013; Hair et al., 2017).
Proceso sistemático para usar la PLS-SEM
Hair et al. (2017) establecieron una metodología que consta de nueve etapas para hacer uso de la PLS-SEM: 1) especificación del modelo estructural, 2) especificación del modelo de medida, 3) recolección de datos y examinación, 4) estimación del modelo, 5) evaluación de medidas formativas, 6) evaluación de medidas reflectivas, 7) evaluación del modelo estructural, 8) análisis avanzados y 9) interpretación de resultados.
Con base en lo anterior, en la etapa inicial de un proyecto de investigación (de manera específica, en esta investigación se ha utilizado el software estadístico SmartPLS), es necesario que primero se presente un diagrama que conecte las variables (constructos) basado en la teoría, es decir, que muestre la lógica de la relación de las hipótesis que se probarán. El modelo se compone de dos elementos: 1) el modelo estructural (llamado también modelo interno en la PLS-SEM) que describe las relaciones entre las variables latentes, y 2) el modelo de medida, que muestra las relaciones entre las variables latentes y sus medidas (sus indicadores). La secuencia de los constructos en el modelo estructural basados en la teoría o lógica son observados de izquierda a derecha. Los constructos independientes (predictores) en la izquierda y las variables dependientes (resultado) del lado derecho. Por lo tanto, la teoría y la lógica deberían siempre determinar la secuencia de los constructos en el modelo conceptual.
Cuando el modelo estructural es desarrollado, se observan principalmente dos aspectos: la secuencia de los constructos y la relación entre ellos, que representan las hipótesis y sus relaciones de acuerdo con la teoría que está siendo probada. Además de observarse las variables latentes y observables, también es importante mencionar dos aspectos que pueden estar inmersos en el modelo en los constructos: la mediación y la moderación.
Respecto de la evaluación sistemática de los resultados de la PLS-SEM, la Tabla 3 muestra las pruebas estadísticas utilizadas tanto para la evaluación de los modelos de medida reflectivos y formativos como en la evaluación global del modelo estructural. Se debe considerar que cada uno de ellos tiene sus propias restricciones para la validez.
La metodología de PLS considera las mismas pruebas estadísticas de los modelos de medida y del modelo estructural (Hair et al., 2017). Sin embargo, es recomendable que los resultados se interpreten en dos etapas; en la primera se deberá analizar la evaluación de viabilidad y la validez del modelo de medida; y en la segunda, la evaluación del modelo estructural (Ibid.; Hulland, 1999; Anderson y Gerbing, 1988). Con respecto a la evaluación del modelo de medida, se evalúan por separado las medidas formativas y reflectivas. Es importante considerar estos aspectos ya que los procedimientos de validación de modelos o medidas formativas y reflectivas son distintos.
De manera general, el proceso sistemático para la aplicación de PLS se debe llevar a cabo a través de dos procesos de evaluación: la preevaluación y la evaluación de los modelos de PLS.
En la etapa de la preevaluación se debe considerar: 1) la especificación del modelo estructural, es decir, el diseño del diagrama que ilustra las hipótesis de la investigación y, por lo tanto, evidencia las relaciones entre las variables a ser examinadas; 2) la especificación de los modelos de medida, que es el que se encuentra definido por el modelo de factor común y el modelo compuesto (reflectivo y formativo); 3) la recolección de datos y análisis de estos, y 4) la estimación del modelo de PLS.
Mientras que en la etapa de evaluación de los modelos de PLS se debe considerar: 1) la valoración del modelo global; 2) la valoración del modelo de medida (en esta valoración, se debe llevar a cabo la evaluación de modelos reflectivos y la evaluación de los modelos de medida formativos), y 3) la valoración del modelo estructural.
PLS-SEM software
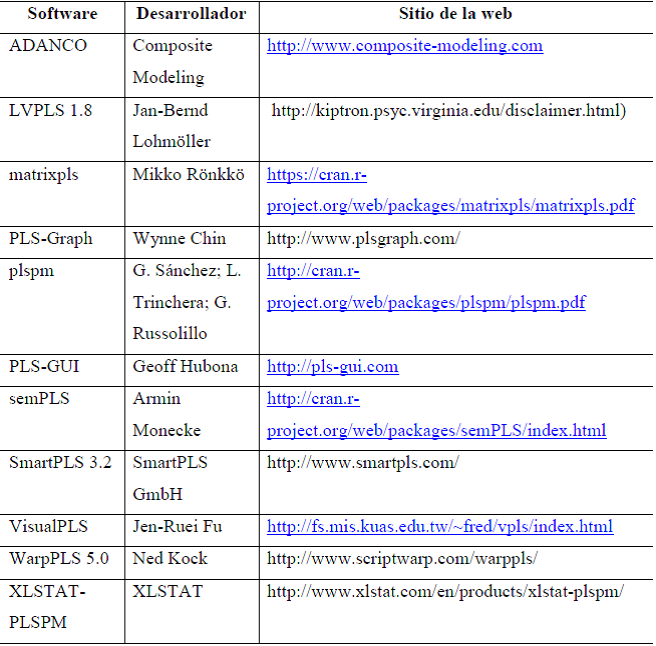
En la Tabla 4 se puede observar el software utilizado para el desarrollo de esta técnica, con base en la propuesta de Roldán y Cepeda (2016, p. 61).
Aplicación de la metodología PLS-SEM: un caso práctico
Con la finalidad de ejemplificar la metodología PLS-SEM se usó información ficticia.
Como primer paso, se presenta un modelo teórico que surge de la revisión de la literatura; en este caso, asumimos que la Figura 3 tiene ese pilar teórico para proponer el modelo a contrastar. Como se observa, tiene cuatro constructos o variables (LT, CO, GC y CS), donde se establecieron cinco hipótesis.
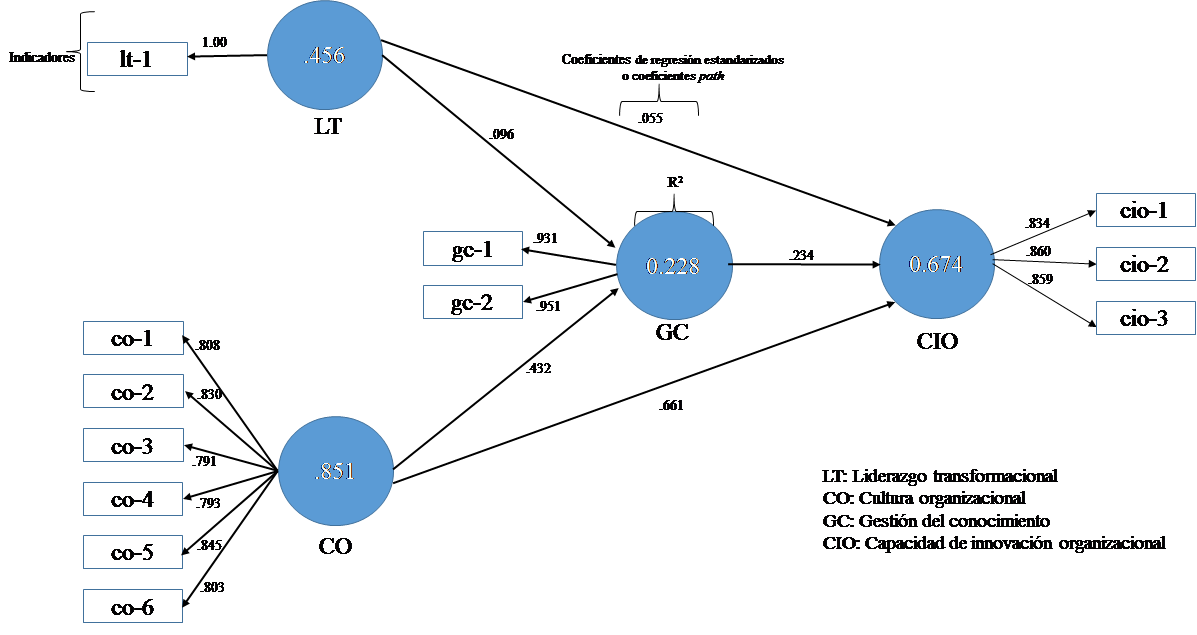
Como segundo paso, es necesario generar las variables observadas (ítems o indicadores); es importante considerar que deben ser formuladas con un soporte teórico de los constructos o variables latentes. En este caso, se optó por medir los constructos latentes con indicadores reflectivos (Figura 4). El liderazgo transformacional (LT) con uno, la cultura organizacional (CO) con seis, la gestión del conocimiento (GC) con dos y la capacidad de innovación organizacional con tres; dando en total 12 reactivos en el instrumento de medición.
Como tercer paso, es necesario generar una base de datos en Excel y exportarla a SmartPLS, la cual se elaboró con la información que reportó el instrumento de medición; en las columnas se codifican los ítems o indicadores y en las filas las observaciones. Cabe resaltar que la base de datos debe ser guardada con extensión CSV (limitado por comas).
Para iniciar el proceso en SmartPLS, se grafica el modelo de investigación (basado en el modelo teórico a contrastar) con el ícono de variable latente y se conectan las variables con la fecha de conector para que, posteriormente, se identifiquen los indicadores de cada constructo o variable. De forma predeterminada, todos los indicadores tienen una dirección reflectiva; en este caso, el software permite hacer el cambio de dirección dando clic derecho en el constructo y seleccionar cambiar entre reflectivo/formativo.
Como cuarto paso, en el menú principal de SmartPLS se calcula el algoritmo de PLS (estimación del modelo), cuyos resultados se observan en la Figura 4. En este modelo se aprecia las cargas factoriales de cada indicador, los coeficientes de regresión estandarizados o coeficientes path y el R2. Cabe señalar que las llaves que se observan en la Figura 4 son meramente indicativas de los siguiente conceptos: indicadores, coeficientes de regresión estandarizados o coeficientes path y del R2.
Como quinto paso, se evalúa el modelo de investigación, el cual requiere de la evaluación del modelo de medida reflectivo y del modelo de medida formativo.
La evaluación del modelo de medida reflectivo se lleva a cabo a través de: 1) la consistencia interna (alfa de Cronbach y fiabilidad compuesta); 2) la validez convergente (fiabilidad del indicador y la varianza media extraída [AVE, por sus siglas en inglés]), 3) la validez discriminante (criterio de Fornell-Larcker) y cargas cruzadas entre indicadores y variables latentes y la ratio heterotrait-monotrail (HTMT).
La consistencia interna indica la fiabilidad del constructo. El software SmartPLS proporciona el índice de fiabilidad compuesta (IFC) y el alfa de Cronbach. La fiabilidad compuesta es más adecuada que el alfa de Cronbach para PLS, al no asumir que todos los indicadores reciben la misma ponderación (Chin, 1998). Nunnally y Bernstein (1994) sugieren validar estos indicadores con un valor de al menos 0.7, considerado como un nivel “modesto” principalmente para investigaciones exploratorias, y valores de 0.8 o 0.9 para etapas más avanzadas de la investigación.
La validez convergente indica que un conjunto de indicadores, ítems o reactivos representan a un único constructo subyacente (Henseler, Ringle y Sinkovics, 2009); lo cual es validado con la AVE, que mide que la varianza del constructo se pueda explicar a través de los indicadores elegidos (Fornell y Larcker, 1981). La AVE deberá ser mayor o igual a 0.50 y proporciona la cantidad de varianza que un constructo obtiene de sus indicadores en relación con la cantidad de varianza debida al error de medida; esto significa que cada constructo o variable explica al menos el 50% de la varianza de los indicadores.
La fiabilidad del constructo o variable latente permite observar la consistencia de sus indicadores; es decir, las correlaciones simples de las medidas o indicadores con su respectivo constructo y valorada examinando las cargas o pesos factoriales (ƛ).
Carmines y Zeller (1979) consideran adecuadas las cargas factoriales mayores a 0.707; por lo tanto, se sugiere que indicadores con cargas menores a este rango deben ser eliminados (Hair, Ringle y Sarstedt, 2011). Cuando un indicador tenga una carga menor al indicado, este podrá ser eliminado y nuevamente correr el modelo para estimar los resultados (Urbach y Ahlemann, 2010). La Tabla 5 muestra valores ficticios cuya finalidad es que el lector pueda observar la consistencia interna, la validez convergente y la fiabilidad del indicador.
Tabla 5 Fiabilidad del indicador y fiabilidad compuesta.
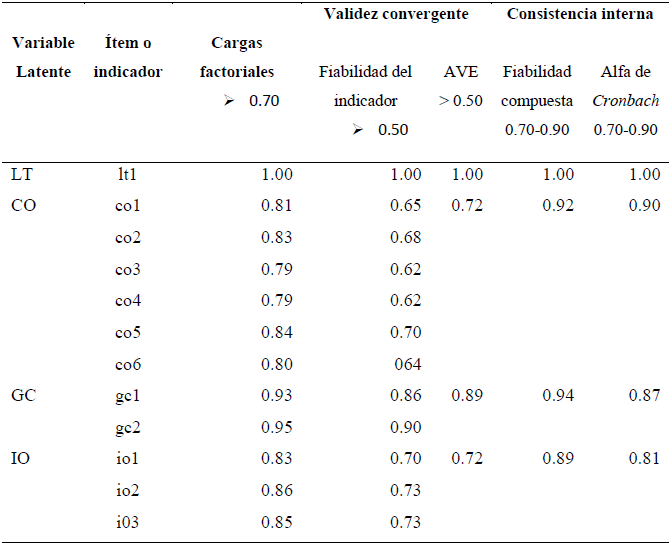
Fuente: Elaboración propia a partir de Hair et al. (2017)
Por otra parte, la validez discriminante indica en qué medida un constructo determinado es diferente de otros constructos. Para valorar la validez discriminante es necesario evaluar tres criterios: 1) criterio de Fornell-Larcker, 2) cargas cruzadas entre indicadores y variables latentes y 3) la matriz HTMT.
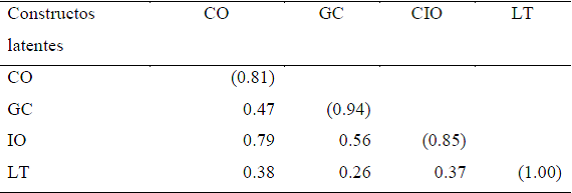
El criterio de Fornell-Larcker considera la cantidad de varianza que un constructo captura de sus indicadores (AVE), el cual debe ser mayor a la varianza que el constructo comparte con otros constructos. Así, la raíz cuadrada de la AVE de cada variable latente deberá ser mayor que las correlaciones que tiene este con el resto de las variables; por lo tanto, para lograr validez discriminante, la raíz cuadrada de la AVE de un constructo debe ser mayor que la correlación que este tenga con cualquier otro constructo, tal y como se observa en la Tabla 6.
Nota: La raíz cuadrada del valor del AVE es mostrada en la diagonal entre paréntesis, los demás datos son correlaciones de las variables latentes.
Por otro lado, es necesario comparar las cargas factoriales cruzadas de los indicadores de una variable latente con las cargas de los indicadores de las demás variables latentes (Tabla 7). Las cargas factoriales deben tener mayor valor con su propia variable que con las demás que se evalúan en el modelo (Barclay, Higgins y Thompson, 1995).
Además, Henseler, Ringle y Sartedt (2016), al realizar estudios de simulación, demostraron que la falta de validez se detecta de mejor forma por medio de la ratio HTMT. Si las correlaciones monotrait-heteromethod (correlaciones entre los indicadores que miden el mismo constructo) son mayores que las heterotrait-heteromethod (correlaciones entre los indicadores que miden diferentes constructos) habrá validez discriminante. Así, la ratio HTMT debe estar por debajo de uno (Gold, Malhotra y Segars [2001] consideran un valor de 0.90). En este sentido, se puede usar también un remuestreo o bootstrapping para probar si la ratio HTMT es significativamente diferente de uno mediante el intervalo de confianza. Conforme a los criterios establecidos, los intervalos de confianza para la HTMT deben ser menores a uno, lo que permite validar este criterio (ver Tabla 8).
Como sexto paso, se evalúa el modelo de medida formativo. El modelo de ejemplo solo incluyó ítems reflectivos. No obstante, es importante mencionar que cuando un modelo de investigación tiene una combinación de constructos reflectivos y formativos es necesario evaluar por separado los diferentes modelos. Se considera funcional mencionar los estadísticos y criterios que se utilizan para evaluar los modelos de medida formativos.
Aunque Diamantopoulos y Winkholfer (2001) argumentan que la evaluación tradicional de fiabilidad y validez en los modelos de medida no es aplicable, debido a que la validez debe ser realizada con base en la revisión exhaustiva de la teoría y con la opinión de expertos, aunado a que las medidas formativas no tienen que estar correlacionadas y están libres de error (Bagozzi, 1994), es importante comentar que Chin (2010) propone que la evaluación de los modelos de medidas formativos sí se debe realizar en dos niveles: 1) a nivel de indicador (multicolinealidad y valoración de las cargas factoriales de los indicadores y su significación) y 2) a nivel constructo (validez externa, validez nomológica y validez discriminante). En la actualidad, Hair et al. (Op. Cit.) consideran que las evaluaciones de los modelos de medida formativos incluyen tres aspectos: 1) validez convergente, 2) evaluación de problemas de colinealidad y 3) evaluación de la significancia y relevancia de los indicadores.
La validez convergente de los modelos de medida formativos se evalúa a través de determinar en qué grado una medida se correlaciona positivamente con otra reflectiva del mismo constructo. Es decir, se crea un constructo formativo como variable predictora (variable exógena) con una variable latente endógena con uno o más indicadores reflectivos. Para evaluar este tipo de validez, es necesario que en el instrumento de medición haya sido definido un ítem o reactivo que englobe todas las mediciones del constructo (a este se le denomina ítem global). La finalidad de este ítem global es que contenga la esencia de la variable latente formativa para que ocupe el lugar de variable exógena. Con esta información se procede a construir un nuevo modelo por cada constructo formativo y se ejecuta el algoritmo de PLS. Cabe precisar que el coeficiente path entre las variables debe tener como valor recomendado mínimo de 0.70 (Ibid.).
Para evaluar el nivel de colinealidad existen diversas pruebas estadísticas. La más usual es el factor de inflación de la varianza (FIV), cuyo valor de manera idónea debe ser mayor a cinco (Ibid.). Otro estadístico es la tolerancia, la cual representa la cantidad de varianza de un indicador formativo no explicado por el otro indicador en el mismo bloque, ambos estadísticos llevan la misma información. En el contexto de la PLS-SEM, un valor de tolerancia abajo de 0.20 y un VIF por arriba de cinco de los constructos predictores implican niveles críticos de la colinealidad. Por otra parte, Belsley (1991) propone usar conjuntamente el índice de condición (IC) y la proporción de descomposición de varianza, efectuados a través de un diagnóstico avanzado de colinealidad dentro de un análisis de regresión múltiple que puede ser calculado por medio del software SPSS. Si una variable tiene un IC mayor a 30 y dos o más variables tienen proporción de varianza alta en el mismo mayor a 0.5, se considera entonces que estas son colineales. Por su parte, Diamantopoulos y Siguaw (2006) consideran que existe alta multicolinealidad cuando el VIF es mayor a 3.3.
Para la valoración de los pesos factoriales de los indicadores y su significación, se debe ejecutar un proceso de remuestreo o bootstraping, en donde si los indicadores tienen una significancia mayor a 0.05 deben ser eliminados. No obstante, al eliminar un indicador formativo, es necesario verificar que no se pierda el significado del constructo. Así, Roberts y Thatcher (2009) recomiendan incluir el indicador en el modelo. En este mismo sentido, Hair et al. (Op. Cit.) sugieren una postura flexible si los pesos factoriales son mayores a 0.05 para no perder el significado del constructo que se está midiendo.
Como séptimo paso, considerando que el modelo reflectivo ha contenido validez y confiabilidad, se procede a evaluar el modelo estructural, en donde se consideran cinco aspectos: 1) evaluación de colinealidad; 2) evaluación del signo algebraico, magnitud y significación estadística de los coeficientes path; 3) valoración del R2; 4) valoración de los tamaños de los efectos (f2), y 5) valoración de la Q2 y de los tamaños de los efectos (q2) (Ibid.).
Respecto de la evaluación de la colinealidad, Hair et al. (Ibid.) consideran indicios de multicolinealidad cuando el FIV es mayor a cinco y el nivel de tolerancia se encuentra por debajo de 0.20. Con los datos ficticios, SmartPLS reportó que los valores de FIV están entre 1.17 a 1.41. Sin embargo, para que los resultados se fortalecieran, se procedió a realizar un diagnóstico de colinealidad por medio de SPSS en el apartado de regresión lineal. Primero se verificó con la variable dependiente IO y las demás variables fungieron como independientes, posteriormente se ejecutó otro proceso en donde se colocó a la variable GC como variable dependiente y a las variables LT y CO como independientes o predictoras. Los resultados del FIV al evaluar las variables de este estudio se encontraron por debajo del valor idóneo, es decir, 1.49, 1.56 y 1.80, respectivamente; no obstante, los valores de la tolerancia sí fueron adecuados con valores por arriba de 0.20.
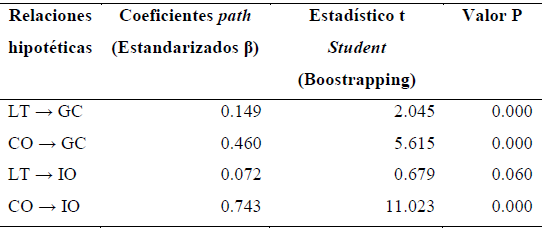
Para la evaluación del signo algebraico, magnitud y significación estadística de los coeficientes de regresión estandarizados (coeficientes path), es importante comentar que estos (coeficientes de regresión estandarizados) muestran las relaciones de las hipótesis del modelo de investigación. En primer lugar, se debe analizar el signo algebraico que fue postulado en la hipótesis: si este es contrario al establecido en la hipótesis, esta no será soportada. En segundo lugar, se analiza la magnitud y la significancia estadística. La magnitud de los coeficientes path se observan como valores estandarizados en un rango +1 a -1; entre mayor sea el valor denota mayor relación (predicción) entre constructos y entre más cercana a 0, menor será la convergencia al constructo. Si el resultado de un valor path es contrario al signo postulado en la hipótesis, indica que la hipótesis no será soportada. El nivel de significancia se determina a partir del valor de la t Student que deriva del proceso de re muestreo o bootstrapping, que es una técnica no paramétrica (no hay parámetros iniciales; se prueba si los caminos entre variables son factibles), la cual evalúa la precisión de las estimaciones de PLS. Cuando en un modelo las hipótesis indican la relación de la dirección (+ ó -), es necesario usar una distribución t de una cola con n-grados de libertad, donde n es número de sub muestras (bootstraping = 5000 sub muestras; t = 0.05; 4999 = 1645; t = 0.01; 4999 = 2327; t = 0.001; 4999 = 3092); para distribuciones de dos colas con n-1 (t= 0.1; 4999 = 1645; t = 0.05; 4999 = 1960; t = 0.01; 4999 = 2577; t = 0.001; 4999 = 3292). Por lo tanto, si el valor empírico de t es mayor que el valor crítico de t, entonces el coeficiente es significativamente diferente de cero; es decir, si el resultado empírico de t está abajo de un determinado valor umbral, significa que no es posible tener confianza en la distribución y así las hipótesis no se verifican.
Como se puede observar en la tabla 9, la relación entre los constructos CO → IO es fuerte (0.743), la relación entre los constructos CO → GC es moderada (0.460) y la relación ente LT → GC es débil (0.149), mientras que la relación entre los constructos LT IO no es significativa.
Se debe considerar que la técnica PLS-SEM, al ser utilizada para maximizar la capacidad de predicción de las variables dependientes, demanda evaluar el R2, el cual representa una medida de valor predictivo. Esto indica la cantidad de varianza de un constructo que es explicada por las variables predictoras del constructo endógeno, cuyos valores oscilan entre cero y uno. Entre más alto sea el valor de R2, más capacidad predictiva se presenta. Falk y Miller (1992) consideran que un R2 debe tener un valor mínimo de 0.10; Chin (1998) considera 0.67, 0.33 y 0.10 (sustancial, moderado y débil); mientras que Hair et al. (2017) recomiendan 0.75, 0.50, 0.25 (sustancial, moderado y débil). En el modelo objeto de estudio (Figura 4) se obtuvo un R2 = 0.674 (valor sustancial) y R2 = 0.228 (valor moderado); lo que implica que la cultura organizacional y el liderazgo transformacional, a través de su efecto sobre la gestión del conocimiento, explican 67.4% de la capacidad de innovación organizacional y un 22.8% de la gestión del conocimiento se explica por el liderazgo transformacional y la cultura organizacional. En este modelo también deberá ser considerado el caso probable de mediación de la gestión del conocimiento entre el liderazgo transformacional y la cultura organizacional con la capacidad de innovación organizacional.
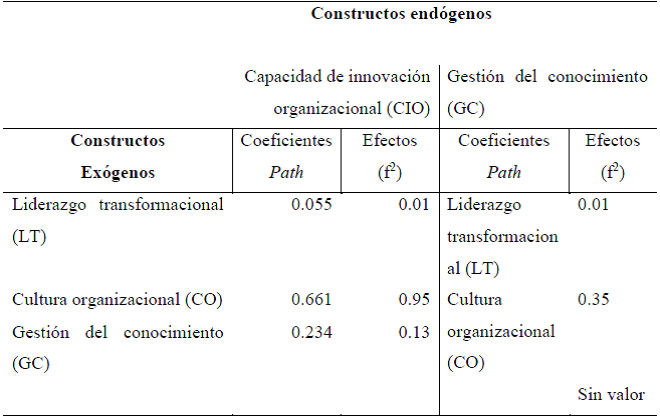
Además de evaluar el valor de R2 de todos los constructos endógenos, es necesario conocer el cambio en R2 cuando un determinado constructo exógeno es omitido del modelo; es decir, el f2 puede ser usado para evaluar si el constructo omitido tiene un impacto sustantivo en los constructos endógenos. Para ello, Cohen (1998) especifica los siguientes valores para evaluar el f2: 0.02 es un pequeño efecto, 0.15 es un efecto medio, y 0.35 es un efecto grande. Como se puede observar en la Tabla 10, la cultura organizacional tiene un efecto grande con la capacidad de innovación organizacional y con la gestión del conocimiento; sin embargo, el liderazgo transformacional tiene un efecto casi nulo con la cultura organizacional y con la gestión del conocimiento.
Adicional al R2 como un criterio predictivo, Hair et al. (2017) recomiendan que los investigadores examinen Q2 para valorar la relevancia predictiva del modelo estructural. Chin (1998) menciona que la relevancia predictiva de los constructos debe ser positiva y con valores mayores a cero; así también Hair et al. (Op. Cit.) establecen valores de 0.02 como valores pequeños, valores de 0.15 como valores medios y valores 0.35 como valores grandes para considerar validez predictiva del modelo.
Geisser (1974) y Stone (1974) recomiendan evaluar la prueba de Stone-Geisser como un criterio de Q2. Para determinar a esta en SmartPLS es necesario generar el procedimiento de blindfolding. Los constructos endógenos del caso ficticio tuvieron una predicción fuerte y media, debido a que Q2 tuvo un valor 0.46 para IO y Q2 tuvo un valor de 0. 15 para GC.
El tamaño del efecto q2 permite evaluar cómo un constructo exógeno contribuye a un constructo latente endógeno Q2 como una medida de relevancia predictiva; el cual puede ser pequeño (0.02), medio (0.15) o grande (0.35). Se observa que los valores son los mismos que el f2 (Cohen, 1998); y su cálculo deriva de la expresión q2 = (Q2 incluida y Q2 excluída)/(1 - Q2 incluida). Este cálculo se realiza de manera manual porque el software SmartPLS no lo proporciona (Hair et al., 2017). De manera muy similar (Tabla 11), el mayor efecto q2 en el constructo de la cultura organizacional con capacidad de innovación organizacional tuvo un valor de 0.661 y la cultura organizacional con la gestión del conocimiento tuvo un valor de 0.15 (efecto pequeño).
Henser, Hubona y Ray (2016) consideran que los resultados del modelo PLS pueden ser evaluados globalmente (modelo general) y localmente (modelos de medida y modelo estructural). En la actualidad, el único criterio de ajuste del modelo global es la normalización de raíz cuadrada media residual (SRMR) (Hu y Bentler, 1998, 1999). Se considera un modelo con un adecuado ajuste cuando los valores son menores a 0.08. Por lo tanto, un valor de 0 para SRMR indicaría un ajuste perfecto y, en general, un valor SRMR inferior a 0.05 indica un ajuste aceptable (Byrne, 2008). Un reciente estudio de simulación muestra que un modelo correcto especificado implica valores SRMR superiores a 0.06 (Henseler et al., 2017).
Recientemente, Albort-Morant, Henseler, Cepeda-Carrión y Leal-Rodríguez (2018, p.1) consideran que en la técnica PLS-SEM, primero se debe hacer la evaluación del ajuste del modelo global mediante: “(i) the standardized root mean squared residual (SRMR); (ii) the unweighted least squares discrepancy (dULS); and (iii) the geodesic discrepancy (fG)”. Posteriormente, realizar la evaluación del modelo de medida, y el modelo estructural.
Conclusiones
El propósito de este artículo científico fue mostrar cómo usar la metodología de PLS-SEM con el uso del software SmartPLS a través de datos ficticios que permitieron evaluar un modelo de investigación (modelo de media, modelo estructural y evaluación global del modelo); en este caso, todo partió de la propuesta del modelo teórico a contrastar que contuvo cinco hipótesis.
Los resultados del modelo de medida mostraron la información necesaria para evaluar la validez de un modelo reflectivo a través de la consistencia interna (alfa de Cronbach y fiabilidad compuesta), de la validez convergente (fiabilidad del indicador y el AVE), de la validez discriminante (criterio de Fornell-Larcker, y cargas cruzadas), y de la ratio Heterotrait-Monotrail (HTMT) de acuerdo con los parámetros establecidos (Carmin y Zeller, 1979; Fornell y Larcker, 1981; Chin, 1998; Nunnally y Bernstein, 1994; Herseler, Ringle y Sinkovics, 2009; Hair, Ringle y Sarsted, 2011; Urban y Ahlemann, 2010; Barclay, Higgins y Thompson, 1995; Henseler, Ringle y Sartedt, 2016; Gold, Malhotra y Segars, 2001). Por lo que respecta del modelo formativo, no se incluyeron indicadores de ese tipo. Sin embargo, se consideró importante mencionar los estadísticos que son necesarios en su evaluación y los criterios establecidos para la validación (Bagozzi, 1994; Diamantopoulos y Winkholfer, 2001; Chin, 2010; Hair, Hult, Ringle y Sarstedt, 2017; Hair, Sarstedt, Ringle y Mena 2012; Belsley, 1991; Roberts y Thatcher, 2009; Hair, Hult, Ringle y Sarstedt, 2017).
Por lo que respecta a la evaluación del modelo estructural, Hair et al. (2017) recomiendan validar el modelo mediante la verificación de coeficientes de colinealidad, de la evaluación del signo algebraico, magnitud y significancia estadística de los coeficientes path, de la valoración del R2, de la valoración de la Q2 y los tamaños de efectos f2 y q2, los cuales fueron considerados para ejemplificar la validación del modelo estructural. Asimismo, se plasmó el análisis de los valores R2 y Q2 como criterios predictivos del modelo y de la metodología PLS-SEM; se comentaron los valores propuestos para la evaluación del modelo estructural (Hair et al., 2017; Falk Miller, 1992; Chin, 1998; Geisser, 1974; Stone, 1974; Cohen, 1998). De la misma manera, para la evaluación global del modelo se comentó el SRMR, considerado como un indicador de ajuste del modelo de PLS-SEM más reciente (Hu & Bentler, 1998; Henseler, Hubona & Ray 2016; Byrne, 2008).
Se concluye que la técnica estadística PLS-SEM es una técnica que ha ganado un gran interés entre los investigadores de las ciencias sociales por ser un enfoque alternativo a la modelación de ecuaciones estructurales. Existen diversas publicaciones en revistas de primer cuartil (top journals) que validan su utilización. Por lo anterior, se anima a la comunidad científica a utilizar esta técnica estadística.











 nova página do texto(beta)
nova página do texto(beta)