Introducción
De acuerdo con Stacey et al. (2015) la producción de alimentos debe incrementarse en un 70 % para el año 2050, lo cual es difícil de alcanzar en un escenario de cambio climático y de agotamiento de recursos naturales. Las zonas de temporal son las más afectadas debido a la variabilidad de la distribución temporal y espacial de la precipitación (Esquivel et al., 2016; Trethowan et al., 2010). Este fenómeno ha provocado reducción en la producción agrícola especialmente en el altiplano semiárido templado del centro-norte de México (Osuna et al., 2019).
Actualmente, el estado de Zacatecas ocupa el primer lugar en la producción de frijol en México, con una superficie cosechada en el año 2019 de 395 mil ha y rendimiento promedio de 0.55 t ha-1. Con respecto al año 2018, la superficie cosechada se redujo en 60 %, debido a que las condiciones climáticas ocasionaron el siniestro de 108 mil ha sembradas (SIAP, 2019). Por esta razón, es necesario contar con herramientas que permitan relacionar la producción agrícola con las condiciones climáticas. La modelación numérica con datos climáticos toma importancia para predecir eventos (Grageda et al., 2012) y pronosticar requerimientos hídricos (Ruiz-Del-Angel et al., 2019). Las redes neuronales artificiales son modelos de caja negra (estáticos o dinámicos) que permiten manejar relaciones no lineales entre variables de entrada y salida de un sistema, mediante elementos llamados nodos y sus interconexiones que imitan las neuronas de los sistemas biológicos (Hagan et al., 1996). Las RNA son modelos capaces de encontrar relaciones de forma inductiva por medio de algoritmos de aprendizaje y datos existentes, utilizadas para clasificar, identificar, diagnosticar, optimizar y predecir, se basan en la analogía del comportamiento del cerebro humano (Fausett, 2006).
Los modelos de redes neuronales artificiales (RNA), han sido utilizados con éxito para tratar problemas en la agricultura moderna, en donde se integran variables climatológicas, del cultivo y manejo. Abraham et al. (2020) compararon los modelos RNA con métodos clásicos, con base en el error medio absoluto (MAE), error cuadrado medio (MSE) y coeficiente de determinación (R2), los autores concluyeron que las RNA tuvieron mejor desempeño para predecir superficie cosechada y producción de soya, mientras que los modelos clásicos fueron mejores para estimar el rendimiento. Khan et al. (2020) utilizaron tres algoritmos de aprendizaje (Levenberg-Marquardt (LM), scale conjugate gradient back propagation (SCG), Bayesian regularization back propagation (BR)) de RNA para predecir la producción de frutas en Pakistán, obtuvieron valores de R2 de 65.6, 70.2 y 76.3 respectivamente y concluyeron que las redes neuronales predicen periódicamente las tendencias de la producción agrícola de frutas. Maimaitijiang et al. (2020) estimaron los rendimientos de tres variedades de soya en Columbia, Missouri, USA, con la implementación de tres técnicas de regresión de mínimos cuadrados parciales (PLSR), regresión aleatoria de bosques (RFR) y redes neuronales artificiales (RNA), utilizando las firmas espectrales, imágenes térmicas y textura del dosel como variables de entrada, concluyeron que el modelo de RNA tuvo el mejor desempeño (R2 = 0.720 y RMSE = 15.9 %).
Una vez que el modelo de RNA ha sido generado, es necesario realizar el análisis de sensibilidad (AS) el cual permite particionar la incertidumbre en cada una de las entradas (Saltelli, 2002), a fin de identificar las variables más importantes que predicen la salida del modelo de RNA. Irigoyen et al. (2012) realizaron un AS en RNA entrenadas para estimar las lámina de riego en maíz (Lr), con componentes del balance de agua (BHC) y estado de desarrollo del cultivo y concluyeron que los BHC son más sensibles para estimar la lámina de riego a los primeros 60 cm de profundidad del suelo.
Asimismo, García et al. (2020) estimaron el rendimiento de grano de maíz con una RNA multicapa, utilizando variables de entrada obtenidas de imágenes multiespectrales y datos colectados insitu y obtuvieron un coeficiente de correlación entre los rendimientos observados y simulados mayores al 85 %, de igual manera, el análisis de sensibilidad mostró que el índice de vegetación y la densidad de plantas tiene mayor importancia relativa para la estimación de rendimiento.
Predecir la producción y rendimiento ayuda a: 1) dirigir los recursos para generar tecnologías que incrementen el rendimiento, 2) enfocar esfuerzos para mitigar el efecto del clima, 3) generar políticas gubernamentales para aumentar la productividad, 4) servir de base para los pagos de seguros y préstamos para la producción de frijol (Intell, 2013; Crane, 2018). Los modelos RNA son capaces de predecir fenómenos altamente no lineales y de allí su utilidad en la determinación de la disponibilidad de grano de frijol con anticipación. Los objetivos del presente trabajo fueron: 1) desarrollar modelos de RNA para la predicción de la superficie cosechada, los rendimientos y la producción de frijol de temporal en el estado de Zacatecas, empleando datos de temperatura máxima y mínima del aire, precipitación y evaporación durante el periodo 1988-2019; 2) realizar un análisis de sensibilidad para determinar cuáles variables de entrada tienen mayor influencia en la producción y rendimiento de frijol. La hipótesis es que los modelos de RNA son capaces de predecir de manera aceptable las variables producción, superficie cosechada y rendimiento de frijol utilizando como variables de entrada factores climáticos y de manejo.
Materiales y métodos
Descripción del área de estudio
La “zona frijolera” en el estado de Zacatecas está ubicada al noroeste del estado, en las coordenadas 23°53´02” latitud Norte y 103°01´33” longitud Oeste, con una altura media de 1883 m.s.n.m. los suelos son tipo aluvión. La precipitación media anual es de 472.4 mm. La mayor precipitación se presenta en los meses de julio-septiembre, en donde se concentra el 63 % de la precipitación anual. La temperatura media anual y máxima mensual es de 16.8 °C y 29.5 °C, respectivamente. La evapotranspiración potencial media de 1 389 mm por año (Medina y Ruiz, 2004). Debido a las características climáticas anteriores la producción de frijol de temporal se lleva acabo de julio a septiembre.
Obtención de datos
La base de datos climáticos (1988-2019) se obtuvo de la estación número 32021 del servicio meteorológico nacional (SMN, 2010) (Estación A), ubicada en la colonia Gonzáles Ortega (-103.44° O, 23.956° N) con datos diarios del 1988 a 2004, y de la estación agroclimática automatizada Col. González Ortega, de la red de monitoreo agroclimático del estado de Zacatecas, CEZAC-INIFAP (Medina et al., 2007) (Estación B), ubicada a -103.45° O, 23.966° N y con datos diarios del 2005 al 2019. Ambas localizadas a 2014 msnm con una separación de 1.5 km, las cuales representan las condiciones climáticas para la producción de frijol de temporal en Zacatecas denominada como la “zona frijolera” (Galindo y Zandate, 2006).
Para el presente trabajo se utilizaron los datos climatológicos de junio a septiembre de: temperatura mínima (Tmin), temperatura máxima (Tmax), precipitación (Pp) y evaporación (Eva) de los meses de julio a septiembre, meses de producción de frijol de temporal en Zacatecas (Medina et al., 2003). Los datos de radiación solar no se incluyen, debido a que no están disponibles durante el periodo 1988 a 2004. Sin embargo, la evaporación la incluye de manera indirecta (SMN, 2010).
Datos faltantes
Fue necesario un preprocesamiento de ambas estaciones climáticas que consistió en: 1) Estimación de datos climáticos faltantes del año 1988 al 2004 de la estación A, 2) Estimación de evaporación de la estación B en función de evapotranspiración potencial, 3) Estadísticas descriptivas de las variables climáticas del ciclo de producción.
La estimación de datos faltantes para la estación A se llevó a cabo utilizando el paquete estadístico R mediante la librería de Climatol (Guijarro, 2018), usando dos estaciones aledañas 32028 y 32054 ubicadas en Juan Aldama y Sombrerete respectivamente. Climatol usa la homogenización de las estaciones para rellenar los datos faltantes a partir de las series más próximas. Se adaptó el método de Paulhus y Kohler (1952), para rellenar precipitaciones diarias mediante promedios de valores aledaños, normalizados mediante división por sus respectivas medias utilizando el método de estandarización de la ecuación 1.
Donde: x es normalizacion de la precipitacion,
Climatol obtiene los parametros anteriores con los datos disponibles en cada
serie, rellena los datos faltantes usando
Donde:
De la estacion B se obtuvieron datos de evapotranspiración potencial (ETo) estimados mediante la ecuación Penman-Monteith (Allen et al., 2006). Raghuwanshi y Wallender (1998) mencionan que hay una relacion entre la evapotranspiracion potencial (ETo) y la evaporacion. Según Silva (1998) la evapotranspiracion potencial (ETo) se puede determinar a partir de las mediciones de evaporacion (Eva) con base en unos coeficientes empiricos que dependen del suelo, tipo de cultivo, regimen de lluvias entre otros factores, como se expresa en la Ecuacion 3:
Donde: K es un coeficiente para el periodo de tiempo determinado, cuyo valor oscila entre 0.5 y 0.9, el cual depende de la intensidad y la distribucion de las precipitaciones. Se utilizo el coeficiente K igual a 0.78 que se obtuvo al relacionar la ETo de la estacion Gonzales Ortega y Eva de la estacion 32021 con los datos existentes del 2007 y 2008 (n=555).
Variables de entrada y salida
Las estadísticas descriptivas de las variables climáticas del ciclo de producción del mes de julio, agosto y septiembre se basaron en los promedios mensuales de las variables climáticas utilizadas, se obtuvieron mediante la siguiente expresión.
Donde:
Se obtuvieron 12 datos por año, de un total de 32 años (1988-2019): Tmax_Jul, Tmax_Ago, Tmax_Sep, Tmin_Jul, Tmin_Ago, Tmin_Sep, Pp_Jul, Pp_Ago, Pp_Sep, Eva_Jul, Eva_Ago, Eva_Sep. Tambien, se obtuvo el valor maximo de la Tmax (TTmax) y el valor minimo de Tmin (TTmin), la precipitación total (SPp) y la evaporacion total (SEva) del ciclo de produccion, dando un total de 16 variables climaticas por ano.
La informacion sobre rendimiento de frijol de temporal (Rto; t ha-1), superficie sembrada (SS; miles, ha), superficie cosechada (SC; miles ha) y produccion (P; t), se obtuvo del Anuario Estadistico de la Produccion Agricola (SIAP, 2019) para los anos 1988-2019, entidad federativa: Zacatecas, cultivo: frijol, ciclo: perenes y modalidad: temporal, obtenidos de los promedios anuales de las variedades y localidades del estado de Zacatecas.
Con el fin de conocer la fuerza de la relacion lineal entre las 16 variables climaticas y superficie sembrada consideradas como variables de entrada, contra rendimiento de frijol, superficie cosechada y produccion incluidas como variables de salida, se realizo un analisis de correlacion (Gogtay y Thette, 2017), previamente al diseno de las RNA’s.
Diseño y entrenamiento de la red
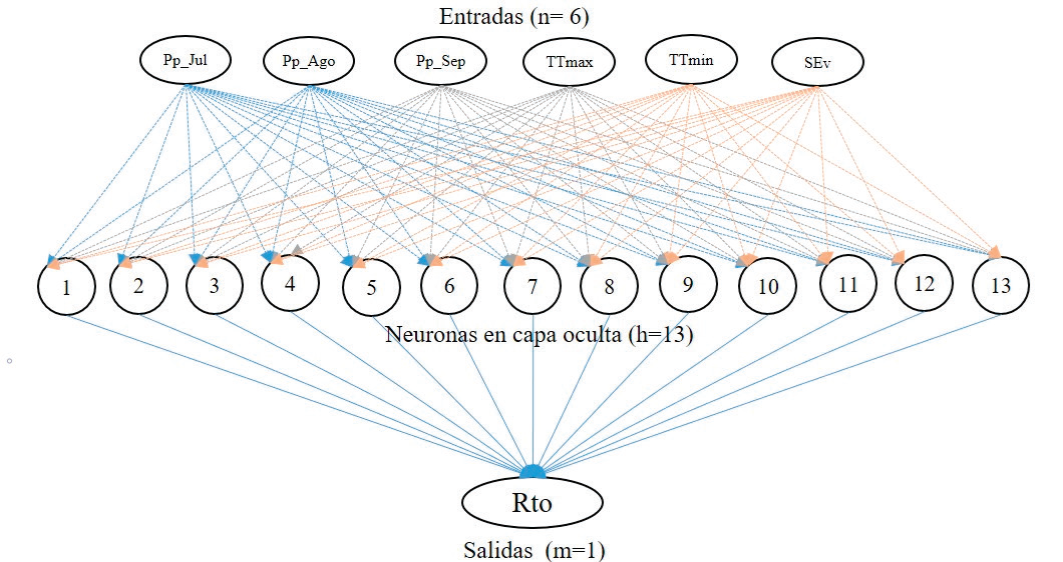
Se implementaron tres redes neuronales artificiales (RNA) con una estructura perceptrón multicapa. Con 16 variables climáticas y la superficie de siembra como las entradas y como variables de salida rendimiento de frijol, superficie cosechada y producción. El número de neuronas en la capa oculta (h) se varió utilizado como referencia los criterios: h=√mn, como límite inferior y h=2n+1 del teorema de Kolmogorov (Kolmogorov, 1957) como límite superior, en donde: n es número de entradas y m es el número de salidas. Las variables de entrada para cada una de las redes se seleccionaron con base a los resultados del análisis de correlación y un estudio exploratorio, combinando las variables de entrada y número de neuronas en la capa oculta. Se utilizó el 95 % de los datos (1988-2017) para el entrenamiento, validación y prueba con 50, 25 y 25 % de los datos respectivamente y el 5 % restante (2018-2019) para la evaluación. El algoritmo de aprendizaje utilizado fue gradiente descendiente con momentum (Garg et al., 2016; Mohamed, 2019) y algoritmo de entrenamiento fue Levenberg-Marquardt backpropagation (LM) (Marquardt, 1963). Para generar los modelos de RNA se realizó un análisis exploratorio combinando las diferentes variables de entrada y número de neuronas en capa oculta hasta alcanzar un buen desempeño.
Todas las RNA se implementaron en MATLAB® con el Toolbox de “Neural Networks” (Demuth et al., 2017; Moore, 2012). La función “newff” se utilizó para crear, entrenar y validar la red, el número de entradas y neuronas en la capa oculta se eligió con base al análisis exploratorio para cada modelo RNA. Se obtuvo el conjunto de pesos óptimos que minimizan el error de acuerdo con la metodología descrita por Chatterjee et al. (2018).
Medidas de desempeño
Para medir el desempeño de la RNA se calcularon: 1) el coeficiente de determinación (R2), (Ecuación 5), (Demuth et al., 2017; Pecar y Davis, 2018), 2) el error medio absoluto (MAE; Ecuacion 6), 3) el error cuadrado medio (MSE; Ecuacion 7); 4) la raiz cuadrada del error cuadrado medio (RMSE;Ecuación 8), (Heng et al., 2009), y 5) la eficiencia propuesta por Nash y Sutcliffe (E; Ecuacion 9) que caracteriza el comportamiento del modelo de simulacion, el modelo perfecto deberia tener una eficiencia cercana a 1 (Krause et al., 2005).
Donde: yi representa el valor observado,
Análisis de sensibilidad
Con el fin de identificar las variables mas importantes para predecir la salida, se implemento el metodo de Garson, que utiliza la matriz de pesos entre la capa de entrada y oculta, y entre la oculta y la capa de salida, se discrimina la importancia relativa de las variables predictoras para una sola variable de respuesta. La contribucion relativa de cada entrada (RIj) esta dada por la Ecuacion 10 (Garcia et al., 2020).
Donde: Wij. -pesos sinapticos de la conexion de entrada i a la capa oculta , Wjo. -pesos sinapticos de la conexion capa oculta j a la salida, m.- numero de neuronas en la capa oculta y n.- numero de capas ocultas.
Resultados y discusión
Datos faltantes
Las variables climaticas diarias de la estacion (32021) Gonzalez Ortega, tuvieron 3.8 % de datos faltantes para precipitacion, temperatura maxima y minima y 2.2 % de datos faltantes para evaporacion (Figura 1). Dado que los datos existentes estan por arriba del 80 % que recomienda la organizacion meteorologica mundial (WMO, 2011), se construyeron series completas a partir de cada subperiodo homogeneo, utilizando “CLIMATOL 3.1.1” (Guijarro, 2018).
Correlación de las variables de entrada y salida
Se consideraron las variables correlacionadas significativamente (p < 0.05), es decir variables con coeficientes absolutos mayores a 0.35 para ser utilizadas en los modelos de RNA para la prediccion del Rendimiento (Rto), Superficie Cosechada (SC) y Produccion (P). En Rto se observaron correlaciones positivas de 0.38, 0.44, 0.36, 0.62, 0.38, y 0.46 para Pp_Jul, Pp_Ago, Pp_Sep, SPp, Tmin_Jul, TTmin respectivamente y correlaciones negativas con valores -0.49 y -0.58 para Tmax_Sep y TTmax. Gourdji et al. (2015) en un trabajo sobre rendimiento de frijol y maiz en Nicaragua con datos historicos del clima encontraron una alta correlacion entre rendimiento de frijol con la temperatura y precipitacion. Wilson et al. (1995) mencionan que el rendimiento de los cultivos esta afectado por precipitacion, radiacion solar y temperatura principalmente. Qian et al. (2006) obtuvo una correlacion de 0.57 entre la radiacion solar y evaporación con datos 1955-2000 en China. Por lo que se incluyo como entrada la SEva para generar el modelo RNA de Rto.
Para SC se observo una correlacion negativa de -0.40, -0.59 y -0.55 para Eva_Ago, Eva_Sep y SEva y una alta correlación positiva de 0.71 con SS. Para P los valores absolutos fluctuaron entre 0.35, 0.36, 0.49, -0.40 -0.47 -0.42, -0.46, -0.5 y 0.39 para Pp_Ago, Pp_Sep, SPp, Tmax_Sep, Tmin_Jul, Eva_Jul, Eva_Sep, SEva y SS, respectivamente.
Con base en los resultados de correlacion y el estudio exploratorio se definieron las variables de entrada de la siguiente manera: RTo → [Pp_Jul, Pp_Ago, Pp_Sep, TTmax, TTmin, SEva], SC → [SEva, SS] y P → [Pp_Jul, Pp_Ago, Pp_Sep, TTmax, TTmin, SEva, SS].
Modelos de Redes Neuronales Artificiales RNA para predicción del rendimiento
Para el modelo de RNA rendimiento se utilizaron: Pp_Jul, Pp_Ago, Pp_Sep, TTmax, TTmin, SEva como variables de entradas y 13 neuronas en la capa oculta (Figura 2). La eficiencia fue de 0.74, la cual es un valor aceptable (> 0.73) de acuerdo con Demuth et al. (2017) y Pecar y Davis (2018). El conjunto de pesos óptimo que minimiza el error cuadrado medio, se obtuvo a las cinco iteraciones.
En la Figura 3 se muestra una comparación entre el rendimiento de frijol observado y estimado por la red neuronal para la etapa de entrenamiento, validación y prueba (1988-2017) y evaluación (2018-2019). En la etapa de evaluación se obtuvo una eficiencia de 0.98 lo que significa que el modelo tiene una buena capacidad de simulación y predicción (Abraham et al., 2020). La eficiencia global considerando la etapa de entrenamiento, validación y prueba y evaluación fue de 86 %.
RNA para predicción de la superficie cosechada
En el modelo de RNA para la predicción de superficie cosechada se utilizaron 2 entradas (SEva, SS) y se varió el número de neuronas en la capa oculta (h) hasta obtener la máxima eficiencia con h=10, mostrando una eficiencia global de 0.85.
La eficiencia en la etapa de evaluación fue de 0.98, lo que significa que el modelo tiene una buena capacidad de simulación y predicción. La Figura 4 despliega el desempeño de la red para la variable de superficie cosechada del cultivo de frijol, la eficiencia global fue de 0.85 para las etapas de entrenamiento y evaluación. Un poco inferior a la presentada por Abraham et al. (2020) que utilizó redes autorregresivas no lineales con entrada externaNARX para predecir rendimiento y superficie cosechada del cultivo de soya en Brasil.
RNA para predicción de la producción
Para la producción de grano de frijol (Figura 5) se utilizaron: Pp_Jul, Pp_Ago, Pp_Sep, TTmax, TTmin, SEva, SS como variables de entrada y 15 neuronas en la capa oculta. La eficiencia encontrada fue de 0.64, en la etapa de entrenamiento, validación y prueba y en la etapa de evaluación la eficiencia fue de 0.65, valor menor a los aceptables (Demuth et al., 2017; Pecar y Davis, 2018). El conjunto de pesos óptimo que minimiza el error cuadrado medio se obtuvo a las seis iteraciones. Debido al bajo desempeño de esta red la producción de frijol se estimó con las predicciones de superficie cosechada y rendimiento obtenidos con los modelos de RNA y se compararon con los datos obtenidos del SIAP (2019). La Figura 5 muestra la producción de 1988 a 2019 en miles de toneladas. Los coeficientes de correlación para la variable de producción fueron de 0.82 y 0.82 para rendimiento y superficie cosechada respectivamente.
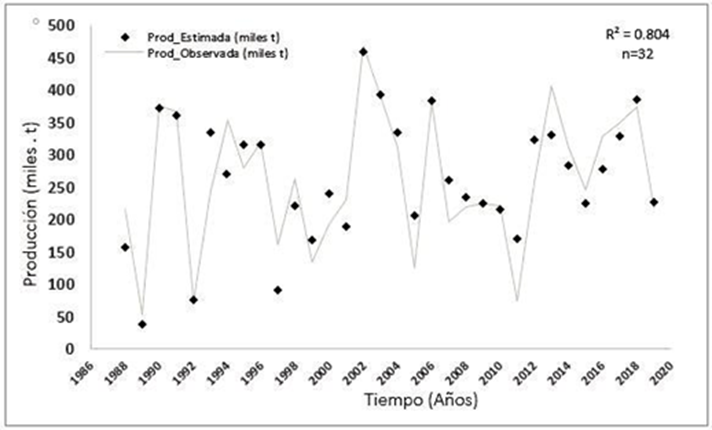
Al estimar la producción con los modelos RNA se obtiene un R2 = 80 %, y puede ser utilizada para simular la producción de frijol en el estado de Zacatecas con datos climáticos y superficie sembrada. Para las tres variables de salida simuladas, se observa un comportamiento estocástico a través del tiempo al igual que las variables climáticas. Tal como lo afirma Geyser y Van (2001) acerca de la relación positiva entre la precipitación y la productividad de maíz. Otros trabajos citados por Gaytán et al. (2014) verifican el riesgo del clima en la producción de cultivos agrícolas para la cobertura de los seguros. De acuerdo con las medidas de desempeño de los modelos de RNA, el modelo para Rto es el que predice mejor en ambas etapas (entrenamiento, validación y prueba y evaluación).
Análisis de sensibilidad
La importancia de las variables predictoras para los modelos obtenidos se muestra en la Figura 6. En el modelo de RNA para simular el rendimiento de frijol, la variable más importante fue la sumatoria de la evaporación (SEva) del ciclo de producción seguida de la precipitación de agosto (Pp_Ago) y julio (Pp_Jul) con una importancia relativa de 21.59 %, 17.64 % y 17.41 % respectivamente. La variable con la mayor importancia relativa en la simulación de la superficie cosechada fue la superficie sembrada (SS) con un valor de 50.11 %, mientras que en el modelo de RNA para estimar la producción las variables más importantes fueron temperatura minina del ciclo de producción (TTmin) y precipitación de agosto (Pp_Ago) con importancia relativa de 20.60 % y 20.21 %, respectivamente.

Para los modelos de RTo y P la variable de mayor importancia fue la precipitación de agosto, cuando el cultivo está en la etapa de floración, esto coincide con lo reportado por Prieto et al. (2019) quienes hicieron un estudio del impacto del clima sobre el rendimiento de frijol en México y concluyeron que el agua es el factor limitante sobre todo en la etapa de floración.
Conclusiones
Los modelos de redes neuronales artificiales generados para predicción de la superficie cosechada y rendimiento de frijol, utilizando variables climáticas y superficie de siembra, mostraron buen desempeño en la etapa de entrenamiento, validación y prueba para un conjunto de 32 años de datos, aunque se debe tener especial cuidado con las fuentes de información y contar con un mayor volumen de datos para que los modelos sean más confiables especialmente en la etapa de evaluación.
Los modelos de RNA generados podrán utilizarse con escenarios futuros de clima artificial para estimar la disponibilidad de grano y evaluación de riegos en los sistemas de producción.
La temperatura mínima del ciclo de producción y la precipitación observada en el mes de agosto, son las variables climatológicas con mayor influencia en la producción de frijol, el comportamiento de dichas variables puede ser un indicador para los productores acerca de la producción esperada. Mientras que la sumatoria de evaporación del ciclo de producción (SEva), fue la variable más importante en la predicción del rendimiento.











 nova página do texto(beta)
nova página do texto(beta)