nova página do texto(beta)
Inglês (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
1 Introduction
Grammatical inference of regular languages is about inferring an automata or a languge from a set of strings, for many years it had been only of theoretical interest, but it has become a problem of practical interest because there are many contexts demanding its use.
Grammatical inference is needed in Speech Modeling in order to build Dialogue Systems between humans and computers, it is also used in Machine Translation Systems. Other areas of application are Robotics and Control Systems, Bio-Informatics, Data Mining [10, 2, 6], Natural Language Processing and Pattern Recognition [15, 5]. The purpose of grammatical inference is to build a model of a target language from a set of strings belonging to the target language, these strings are called the positive sample, a negative sample (set of strings not belonging to the target language) can also exist [2].
There exist many approaches to solve this problem, ranging from formal languages and automata theory to statistic and merges of them. Some approaches only need the training sample to do the job, the proposal presented here is one of them, others need additional information.
The structure of this paper is the following. In Section 2, some works about grammatical inference are described. The corpus used for the training process is presented in Section 3. The proposed model is reported in Section 4. The obtained results are shown in Section 5. Future work and conclusions are stated in Section 6.
2 Preliminaries
Grammatical inference of regular languages has evolved in its theoretical development and in its practical use. In this way, some works considered important in this field are described in this section.
In the first place, in [12], Gold proposed a model for language identification in the limit, setting the bases for automata inference and providing a tool to prove the correctness of algorithms for grammatical inference. In [13] Gold proved that to find the minimal deterministic finite automaton (DFA) consistent with a set of positive and negative samples is a NP-complete problem.
In [3, 4], Angluin showed that to find the minimal DFA from a set of samples continues being NP-complete, even if the target automaton has only two states, or if a few strings are missing in the training data set.
In addition, in [3], it was proved that the problem continues being intractable even though the algorithm can ask oracle questions about wheter a string belongs to or not to the target language; or if the current hypothesis is equivalent to the target automaton.
Carrasco et al. [8] presented an algorithm that builds an stochastic deterministic automaton from the set of samples. Coste et al. [9] proposed to construct a nondeterministic finite automaton (NFA) as a particular case of non ambiguous finite automata.
3 Description of the Corpus DIHANA
The corpus DIHANA [7] is the data set used in this work. It is a corpus in spanish language composed of 900 dialogues about telephonic queries of schedules and prices of long distance train tickets. It was acquired from 225 different speakers (153 men and 72 women). There are 6,280 user turns and 9,133 system turns. The vocabulary size is about 839 words.
The corpus was acquired by the Wizard of Oz technique. The acquisition was restricted at the semantic level, but it was not restricted at the lexical or syntactic levels (spontaneous speech). The tagging of the speeches follows the scheme Speech Acts as it is described in [1].
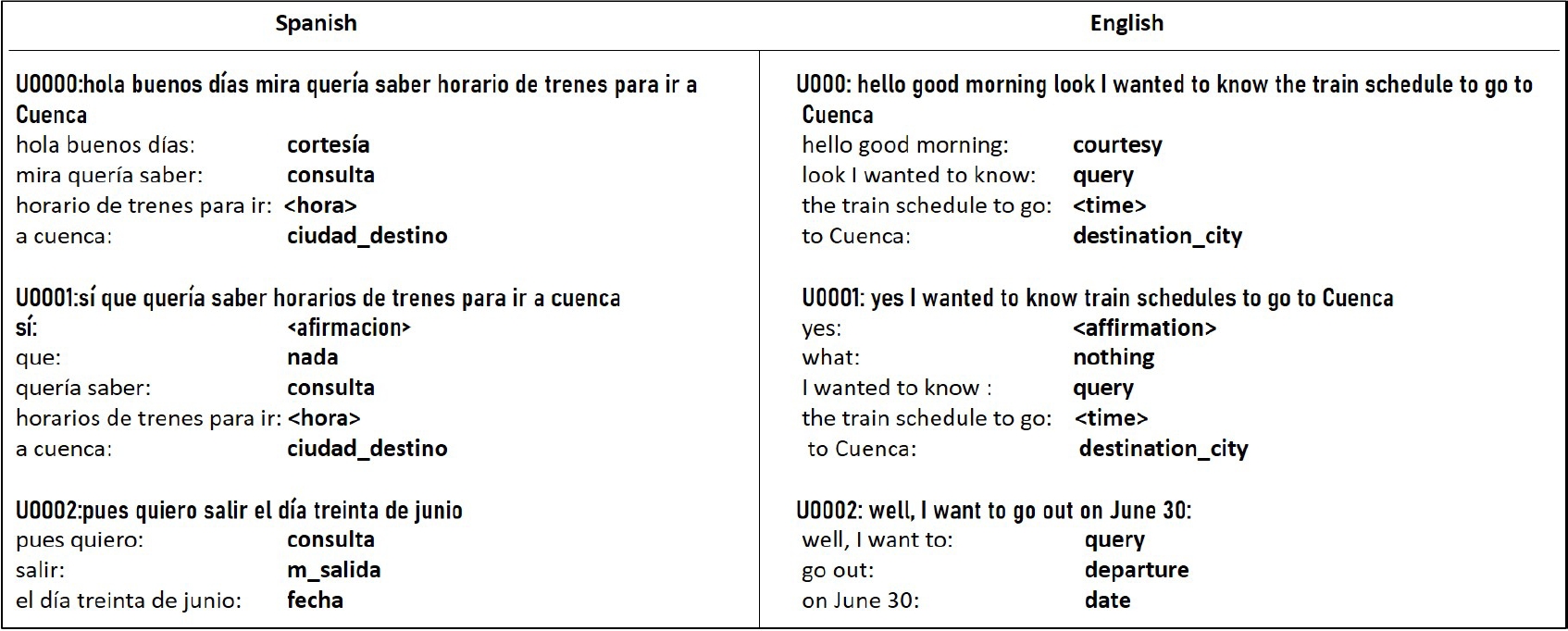
Table 1 shows de main characteristics of the DIHANA tagged corpus. Figure 1 shows an example of three typical dialogues in the DIHANA corpus, the tags of the semantic components were obtained using the Named Entity Recognizer (NER) of Stanford [11] as it is shown in [14].
Table 1 DIHANA main characteristics
| Characteristic | Total | User | System |
| Turns number | 15413 | 6280 | 9133 |
| Segments number | 23542 | 9712 | 13830 |
| Average of segments by turn | 1.5 | 1.5 | 1.5 |
| Dialogues number | 248 | 153 | 95 |
The sequences of semantic components obtained by the NER for each one of the dialogues in Figure 1 are shown in Figure 2, the main idea of this proposal is to take the semantic components as symbols, hence each sequence of semantic components forms a string, from these strings an automaton is inferred.
4 Automata Inference
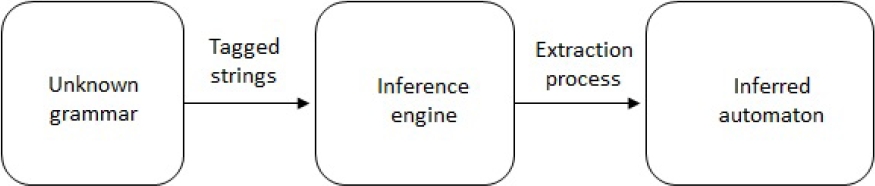
Grammatical inference consists of finding or learning an automaton or a grammar from a finite set of strings called training sample. The problem can be seen as designing an inference engine that learns and extracts an automaton from the finite set of strings, this is shown in Figure 3.
The model proposed in this work follows the steps shown in Figure 3. In the first place, a set of dialogues are taken from the DIHANA corpus, the corpus is tagged as it is described in [7, 1], the tags of the corpus are the semantic components (Figure 1) assigned by the Stanford NER [11] as it is described in [14].
The sequences of semantic components are the input of the inference engine, the engine was implemented in the awk language.
The objective of the inference engine is to construct an automaton, this automaton is our model of valid dialogues.
In Figure 4 a segment of the inferred automaton is presented. The number appearing after the word label refers to the frequency of occurrences of a pair of semantic components. For example: Inicio−>p_afirmacion[label=‘1’] indicates that the pair of semantic components Inicio and p_afirmacion appears one time. The line p ciudad destino[shape=doublecircle] means that the semantic component p_ciudad_destino is a final state of the automaton.
5 Experimental Results
The training sample used to construct the model contains 4,020 dialogues. The assessment of the model was done via 10 fold cross validation. The accuracy reached is 96.75% and it is the average of the ten iterations performed. In Table 2, a summary of the 10 fold cross validation is presented.
Table 2 Summary of the 10 fold cross validation
| Iteration | Training | Test | Accepted | Rejected | Accuracy |
| 1 | 3618 | 402 | 374 | 28 | 93.03 |
| 2 | 3606 | 414 | 400 | 14 | 96.61 |
| 3 | 3564 | 456 | 437 | 19 | 95.83 |
| 4 | 3615 | 405 | 393 | 12 | 97.03 |
| 5 | 3616 | 404 | 395 | 9 | 97.77 |
| 6 | 3632 | 388 | 369 | 19 | 95.10 |
| 7 | 3614 | 406 | 395 | 11 | 97.29 |
| 8 | 3639 | 401 | 398 | 3 | 99.25 |
| 9 | 3641 | 379 | 371 | 8 | 97.88 |
| 10 | 3621 | 399 | 390 | 9 | 97.74 |
6 Conclusion and Future Work
The main goal of this work was reached because the inferred automaton is a strong model, its accuracy is 96.75%. The assessment of the model points to the same conclusion as it is shown in Table 2. As future work it is needed to extend the model in order that it can recognize dialogues of the kind question-answer.
