Introducción
La ciudad es, quizá, el invento más importante en la historia de la humanidad (Glaeser, 2011). El mundo del siglo XXI es un mundo de ciudades, y en ellas, sobre todo en las de mayor jerarquía, se juega el futuro de los países y sus regiones (ONU-Hábitat, 2008). Son un activo estratégico de las sociedades: motores imprescindibles del crecimiento económico y el desarrollo humano (Banco Mundial, 2010; Storper, 2013). Para que cumplan cabalmente su función, deben planearse cuidadosamente salvaguardando su sostenibilidad y estar respaldadas por un campo fuerte (Sobrino et al., 2015).
México registraba en 2010 once metrópolis con más de un millón de habitantes, pero antes de 2030 serán 21 las urbes millonarias. Es decir, en los próximos años el país duplicará su capital urbano de gran escala y la tendencia será creciente (Garrocho, 2013). Estas ciudades millonarias deberán ser motores potentes del desarrollo de la nación y sus regiones. Si el país planea la sostenibilidad de sus ciudades, podrá aprovechar este bono urbano; de lo contrario, perderá la oportunidad (como ocurrió con el bono demográfico) y se encontrará con una realidad caracterizada por ciudades-problema (Garrocho y Sobrino, 2018). El reto es serio.
Las ciudades son producto del pacto social, y su planeación debe apoyarse en procesos colectivos de consulta y codiseño (Wagner y De Vries, 2019). No puede cumplirse el contrato social sin participación social (Giddens, 2013). Sin embargo, los ciudadanos difícilmente podrán contribuir activa e informadamente al codiseño de la metrópoli sin disponer de desarrollos científicos y tecnológicos automatizados (Unsworth, Forte y Dilworth, 2014). La planificación de las ciudades en México (y en muchos otros países) está rezagada en este tema. Existe una necesidad urgente de desarrollar nuevos métodos y mejores herramientas para apoyar la toma de decisiones urbanas, especialmente a nivel local (Wagner y De Vries, 2019). En un mundo que depende de sus ciudades, es cada vez más necesario disponer de modelos urbanos interactivos, prácticos, apoyados en conocimientos, herramientas y tecnologías de frontera, capaces de apoyar procesos colectivos de consulta y codiseño de nuestras metrópolis (Angilella et al., 2016).
Este trabajo avanza en esa dirección. Combina geografía urbana, matemáticas para sistemas dinámicos, tecnología y ciencias computacionales, con el fin de alcanzar los siguientes objetivos:
Diseñar un método de modelado de carácter general fundamentado en Autómatas Celulares en Cascada (ACC), que permita construir modelos operativos específicos de la expansión de las ciudades mexicanas. El método y sus modelos deben considerar múltiples restricciones al crecimiento físico de la urbe (e.g., calles, espacios públicos, áreas no urbanizables por normatividad, por razones ambientales o por límites político-administrativos, entre muchas otras). El método debe estar automatizado para que sea práctico y su costo de operación debe estar acorde a las capacidades financieras de los gobiernos locales.
Someter el método propuesto a una prueba empírica que mida su capacidad para generar modelos de simulación de la expansión urbana en ciudades mexicanas. Es decir, valorar la bondad de ajuste entre las simulaciones de los modelos construidos con nuestro método y la expansión urbana observada en tres ciudades seleccionadas por sus características contrastantes: las áreas metropolitanas de Toluca, Tijuana y Acapulco (en adelante omitiremos el término área metropolitana para evitar ser repetitivos). Valoramos los resultados del modelo con indicadores de bondad de ajuste global y local entre mapas (v.g., imágenes), articulados en un filtro en cascada diseñado para este trabajo.
Ilustrar la aplicación de nuestro método de modelación para alimentar políticas urbanas relacionadas con la expansión de las ciudades.
Estrategia de presentación
En lo que sigue, el documento se organiza de la siguiente manera: en la sección 1 destacamos algunas de las ideas claves para este texto vinculadas con los modelos urbanos basados en autómatas celulares (AC). Evitamos repetir complejidades matemáticas de los AC que se aclaran en innumerables publicaciones y nos concentramos en explicaciones conceptuales con un enfoque didáctico que permea a lo largo de todo el documento (por eso las diversas notas al pie de página). En la sección 2 explicamos en detalle el método de modelado que proponemos, al que hemos llamado Autómatas Celulares en Cascada (ACC). Este método mejora el trabajo de Jiménez, Chávez y Garrocho (2018) y es capaz de incluir numerosas restricciones a la expansión de las ciudades. Luego, en la sección 3, recuperamos los argumentos y el método revisados en las secciones anteriores, y sobre esa plataforma instrumentamos nuestro método de modelado en las tres urbes bajo experimentación. La idea es identificar, para cada una, el modelo de ACC que registra los mejores indicadores de bondad de ajuste entre sus simulaciones de la expansión urbana y la expansión urbana observada, y valorar los resultados. Más adelante, en la sección 4, mostramos la utilidad de nuestro método de modelado para explorar escenarios de planeación urbana. Construimos un modelo para simular un escenario donde la expansión de Toluca se restringe en zonas estratégicas por su importancia hídrica (además de que, por supuesto, se restringe el crecimiento de la ciudad en sus vialidades, espacios públicos y otras áreas donde no puede expandirse). Finalmente, en la sección 5 presentamos las conclusiones del trabajo, subrayamos sus aportaciones y, lo más importante, derivamos una apasionante agenda de investigación para continuar avanzando hacia la disponibilidad de modelos urbanos que apoyen de manera práctica procesos colectivos de consulta y codiseño de las ciudades de México y, quizá, de algunos países latinoamericanos. El texto cierra con un listado de la bibliografía consultada.
1. Antecedentes: Autómatas Celulares en Cascada (ACC) y el modelado de las ciudades
Los autómatas celulares (AC) son, tal vez, el enfoque más utilizado desde hace varias décadas para representar cambios espacio-temporales en el territorio (Wahyudi y Liu, 2016). Las razones son diversas: son prácticos y robustos para procesar imágenes, reconocer y proyectar patrones en tiempo y espacio (Wongthanavasu y Tangvoraphonkchai, 2007); no requieren demasiados datos que son costosos de recolectar (lo que los hace mucho más operables que los modelos integrados urbanos: Lopes, Grangeiro y Van Wee, 2019); y facilitan simular numerosos procesos espaciotemporales: cambios de uso del suelo (Baxendale y Buzai, 2011; Pérez-Miranda et al., 2011; Padilla et al., 2015), difusión de contaminantes (Marín et al., 2000), deslizamientos de tierra (Lai y Dragicevic, 2011), propagación de incendios (Yassemi, Dragićević y Schmidt, 2008), entre otros.
El tema de la información que se requiere para operar modelos urbanos es central (vale la pena revisar al respecto el artículo clásico y aún válido de Lee Jr., 1973). Comparados con los modelos integrados urbanos (véase la excelente revisión de Lopes, Grangeiro y Van Wee, 2019), los basados en AC requieren poca información, privilegian la calidad sobre la cantidad de los datos, y muchos de ellos permiten recuperar la experiencia, el conocimiento y la sensibilidad de los agentes interesados en la ciudad (v.g., información cualitativa/ subjetiva). Todo esto es relevante en ciudades de países en desarrollo, como México, porque se reduce notablemente el costo de operar modelos para la toma de decisiones urbanas, especialmente en la escala local (Clarke, 2018).
Una de las áreas donde más se han aplicado los modelos de AC es en la simulación de la expansión urbana (Aburas et al., 2016; Clarke, 2018). La razón principal de su predominio es que los AC permiten simular el crecimiento de las ciudades representando el espacio y el tiempo en términos discretos, lo que resulta muy atractivo y práctico para modelar procesos urbanos de manera exploratoria y/o experimental (v.g., ex ante la toma de decisiones), generar escenarios y alimentar el diseño de políticas urbanas (Rocha-Campos, De Almeida y Pereira de Quiroz, 2018). Todo a bajo costo, sin requerir grandes cantidades de datos y sin necesidad de estimar la complejidad casi inmanejable de las inagotables relaciones entre variables de los modelos urbanos integrados (también llamados holísticos) (Wahyudi y Liu, 2016).
La aplicación de modelos basados en AC se ha vuelto cada vez más útil en el análisis urbano, sobre todo cuando se vincula con sistemas de información geográfica (SIG), se desarrolla el software ad hoc (Li, Liu y Yu, 2014) y se aprovechan la experiencia y el conocimiento científico e intuitivo del humanware (Chávez y Garrocho, 2018). En estas circunstancias, crece exponencialmente la capacidad para utilizar grandes bancos de datos socioespaciales (de acceso abierto, como los del INEGI en México) y la información de que disponen los ciudadanos. Con estas referencias y aplicando reglas de transición relativamente simples, es posible generar patrones urbanos complejos que evolucionan en el espacio y el tiempo, simulando de forma eficiente y cada vez más precisa la expansión observada de la ciudad (Kim y Batty, 2011).
Es importante subrayar que aquí entendemos los modelos urbanos como Louf y Barthelemy (2014). Es decir, como herramientas que representan una realidad simplificada con fines exploratorios y/o experimentales de escenarios urbanos probables que eventualmente, cuando alcanzan cierto grado de maduración, permiten probar razonamientos teóricos, explicar realidades empíricas y hacer previsiones condicionadas. Bajo ninguna circunstancia los consideramos instrumentos predictivos.
En los modelos AC usualmente se adopta un proceso de arriba hacia abajo para simular patrones y procesos de expansión urbana, tanto en el espacio como en el tiempo (Jiménez, Chávez y Garrocho, 2018). Por un proceso de arriba hacia abajo entendemos que el modelo aplica las reglas de transición de manera determinista comenzando por la esquina noroeste de la matriz de datos espaciales (e.g., la mancha urbana procesada), avanzando renglón por renglón, de izquierda a derecha y en orden descendente. En cambio, en el modelo de ACC que presentamos más adelante, las reglas de transición no responden a un patrón de arriba hacia abajo, sino que se selecciona el punto de aplicación inicial de manera aleatoria, lo que reduce notablemente el determinismo del modelo (Lansing, 2003; Holland, 2006).
En términos generales, cuando se utilizan AC para modelar la expansión urbana con visión macroscópica, es común que surjan dos problemas claves: i. se complica incorporar al modelo la aparición de nuevas áreas urbanizadas dispersas; y ii. es difícil restringir la expansión en zonas donde el crecimiento no se permite o resulta imposible la construcción de nuevas urbanizaciones para vivir y/o trabajar (e.g., por razones físicas, de planeación y gobernanza, administrativas, legales, medioambientales, históricas) (Rasmussen y Hamilton, 2012). Para resolver este problema, aquí usamos Autómatas Celulares en Cascada (ACC). Dado que los modelos urbanos basados en ACC son centrales para este trabajo, los explicamos con detalle en la siguiente sección.
2. Metodología de los Autómatas Celulares en Cascada para modelar la expansión urbana
La clave para desarrollar modelos de AC que incorporan información múltiple en sus reglas de transición radica en mejorar su capacidad para representar la complejidad de la expansión urbana a diferentes escalas espacio-temporales (O’Sullivan y Torrens, 2000; Benenson y Torrens, 2004). Eso es justo lo que se hace en este trabajo. Implementamos un modelo ACC con el fin de replicar la expansión de la mancha urbana entre 2013 y 2017 de dos ciudades mexicanas y una en el periodo 2003-2017 con características contrastantes, considerando más información que la manejada en los modelos AC tradicionales. Específicamente, consideramos zonas urbanizadas dispersas y zonas restringidas a la urbanización.
El nuestro es un método de modelado híbrido automatizado que conjuga ACC en ambiente SIG, lo que sitúa al trabajo en los campos de la geosimulación (Benenson y Torrens, 2004) y la GIScience (Goodchild, 2013). Este desarrollo (llamado Cyborg: Simulador Urbano) es sólo uno de los varios módulos que se han implementado en la Estación de Inteligencia Territorial: Christaller, en El Colegio Mexiquense (Chávez y Garrocho, 2018; Jiménez, Chávez y Garrocho, 2018; Jiménez, 2019).1
La parte experimental de este trabajo se basa en la aplicación de reglas de transición local semideterministas que siguen la lógica de un AC, donde la adyacencia se define a partir del criterio de contigüidad de Moore (Wolfram, 1983). Al hablar de reglas de transición local semideterministas, estamos proponiendo una ubicación aleatoria de un pixel en una rejilla bidimensional, al que se le aplica inicialmente la regla de transición determinista (F) mostrada en la Ecuación[1], que es un número de base 10 que va del número 0 al 255, es decir, F ( [0, 255].2
donde: G es el arreglo dimensional del modelo, que puede ser de una, dos o tres dimensiones (aunque en el análisis urbano predominan ampliamente los modelos en dos dimensiones: Chen, 2018); S es el conjunto finito de estados discretos de las celdas; N representa las celdas vecinas; y F es la regla de transición que determina cómo el estado actual de una celda va a cambiar en el próximo lapso de tiempo.
Este número de base 10 se traduce en su equivalente de base 2 (binario), que puede ser utilizado por los modelos ACC. Para los experimentos de este trabajo, las condiciones iniciales provienen de mapas raster a los que se les realizó un proceso de filtrado para binarizarlos. Con los mapas ya binarizados, las herramientas de Christaller permiten instrumentar el modelo de ACC semideterminista.3
La simulación y construcción de escenarios de la mancha urbana inician con la búsqueda aleatoria en el mapa raster de la ciudad, del bit (v.g., celdas o células) donde va a iniciar la aplicación de las reglas de transición. Esto se hace de la siguiente manera:
Se obtienen los mapas de las ciudades en formato raster del satélite LandSat para los años seleccionados (en este trabajo, 2013-2017 para dos ciudades, y 2003-2017 para una más). Aquí utilizamos una resolución muy alta: pixeles que representan 15 x 15 metros.4 Se hace un filtrado del mapa raster para reclasificar los pixeles en 1 (suelo ocupado) y 0 (suelo vacante). De esta manera se obtiene un mapa binario.
Las áreas restringidas se delimitaron con mapas vectoriales para 2016 y 2017. Se usó cartografía del INEGI y de Conabio. El proceso inició descargando cada una de las capas de restricciones. Se validó la proyección y escala de los datos y se revisaron visualmente los elementos sobre un mapa raster. Se realizaron correcciones finas en las capas vectoriales y se rasterizó cada una de las capas. Esto implicó compatibilizar las fuentes vectoriales con la imagen raster y extraer la zona de estudio para cada capa de restricción. Posteriormente, mediante el SIG se generó una combinación de todas las capas raster ya tratadas y se binarizó la imagen resultante. El tiempo total de procesamiento de restricciones para las tres ciudades fue de alrededor de diez horas.
Un ejemplo de las condiciones iniciales de las imágenes en formato binario se muestra en la Figura 1. Mediante una búsqueda aleatoria identificamos los vecinos: X, X - 1, X + 1 (Figura 2). El número de procesos de búsqueda depende de las dimensiones de la imagen (m × n), que en nuestro caso son las celdas o pixeles a lo ancho (m) y a lo largo (n) del mapa de entrada. Esto define cuántas veces se va a recorrer la superficie donde están contenidos los ceros y unos en el mapa raster.
El principio de adyacencia y la regla de transición producen el estado de la estructura espacial en cada lapso de tiempo (t), que en nuestro ejemplo implica la búsqueda de otro dato en la matriz. En un AC unidimensional, el espacio consiste de un solo renglón de células a las que se aplica un principio de adyacencia básico de dos vecinos por célula, y a los que se administran condiciones de frontera.5
El modelo genera el estado del sistema espacial en el siguiente renglón de la matriz. Por ejemplo, si existe vecindad con una celda con valor 1 (v.g., urbanizada), como se muestra en la secuencia de la Figura 2. Con esto se garantiza que la rejilla donde se ubica el mapa binario de la ciudad bajo experimentación no crezca fuera de las dimensiones de la imagen base, que es más extensa que el área urbana observada.
Las reglas de transición que utilizamos en este trabajo son aplicables a tres bits, y se tienen 256 reglas. El punto clave es detectar la regla de transición que mejor simule el proceso de expansión urbana, del conjunto de las 256 reglas posibles (Fúster-Sabater, Pazo-Robles y Caballero-Gil, 2008). Para lograrlo, se requiere, por lo menos, cumplir dos condiciones: a) correr el proceso con todas las reglas de transición (las 256, lo que supone la construcción de 256 modelos de expansión urbana para cada ciudad bajo experimentación); y b) contar con un instrumento, que en nuestro caso es el filtro en cascada, que mida la bondad de ajuste que se logra con cada regla de transición entre el área urbana observada y la calculada por los modelos ACC. Adicionalmente, generamos un banco de pruebas con el fin de construir escenarios a 14 años para la ciudad de Toluca.6
El método de modelado ACC propuesto en este trabajo incluye un parámetro estocástico para seleccionar la celda donde inicia la aplicación de cada regla de transición. Esto es importante porque reduce el carácter determinista de los modelos, minimiza el problema ocasionado por la aparición de áreas urbanizadas dispersas (no contiguas a la ciudad) y permite marcar zonas donde no se permite o es imposible la construcción de nuevas urbanizaciones para vivir y/o trabajar, lo que facilita modelar áreas urbanas complejas, simular escenarios más realistas que con los AC tradicionales, y hacer corridas exploratorias y/o experimentales. El resultado son modelos de expansión urbana más útiles para la toma de decisiones, ya que es posible explorar escenarios de expansión urbana que ayuden a anticipar tendencias, así como valorar las consecuencias e impactos de distintas acciones/ inacciones urbanas (Aguilera, 2006; Martner, 2016). En la sección 4 ilustramos algunas de estas posibilidades.

Fuente: Elaboración propia.
Figura 1 Condición inicial de un mapa filtrado para el análisis de Autómatas Celulares en Cascada

Fuente: Elaboración propia.
Figura 2 Nueva transición en el ACC: crecimiento programado si existen vecinos cercanos
Es interesante notar que aportamos una técnica que permite identificar la regla de transición que mejor replica la realidad observada, a la que hemos llamado filtro en cascada. Esta técnica incorpora indicadores globales de bondad de ajuste (v.g., a escala de ciudad) e identifica la coincidencia de pixeles, lo que permite develar la regla de transición que reporta el mejor ajuste entre la expansión observada de la ciudad y la generada por cada modelo (Figura 3).
Cada indicador que utilizamos en el filtro mide aspectos claves del proceso de expansión urbana y son ampliamente reconocidos en la literatura (Clarke, 2018): i. entropía de Shannon, que estima lo compacto o disperso de la mancha urbana (Bhatta, Saraswati y Bandyopadhyay, 2010; Cabral et al., 2013);7ii. dimensión fractal, que sintetiza el crecimiento y la forma de la mancha urbana (Chen, 2018; Shen, 2002);8iii. índice de Kappa de Cohen, que mide la similitud entre dos mapas descontando la coincidencia esperada por el azar (López-de-Ullibarri y Pita-Fernández, 1999; Abraira, 2001; Viera y Garrett, 2005);9 y iv. índice de Jaccard (también conocido como coeficiente de similitud de Jaccard), que mide la similitud de la localización de las celdas considerando su información, y es el indicador de ajuste más reportado en la literatura sobre similitud de imágenes (Guan y Rowe, 2016).10 En Jiménez, Chávez y Garrocho, 2018, y Jiménez, 2019, se presenta una detallada explicación de estos indicadores y su operación en el ambiente de Christaller.
El objetivo del filtro en cascada es develar el o los modelos que mejor replican la mancha urbana observada, considerando cada una de las 256 reglas de transición (comparando cada uno de los 256 modelos resultantes), así como reducir el tiempo de procesamiento computacional de los modelos (Figura 3). Esto se logra comparando los valores de los indicadores de la entropía de Shannon y de la dimensión fractal de la mancha urbana observada en t+1 (v.g., 2017) contra los valores de las manchas urbanas producidas por los modelos, que tuvieron como insumo la mancha urbana observada en t (v.g., 2013). La comparación es sencilla porque sabemos que el indicador de la entropía de Shannon relativizado varía entre 0 y 1 (Bhatta, Saraswati y Bandyopadhyay, 2010) y que el de la dimensión fractal varía entre 1 y 2 (Shen, 2002).
Cuando el índice de Kappa de Cohen es 1.0 significa que hay una coincidencia perfecta entre los pixeles de dos imágenes (e.g., mapas), y cuando es 0.0 significa que la coincidencia entre las dos imágenes es igual a la que se esperaría por azar. Por su parte, el índice de Jaccard también mide la similitud entre dos imágenes (e.g., mapas), pero en términos del estado y de otra información externa del pixel (e.g., diversas variables sociales, físicas, institucionales, que en este trabajo aún no incorporamos). En otras palabras, el índice de Jaccard mide la superposición coincidente de pixeles (por localización y estado) entre una imagen de referencia (v.g., un mapa que representa la expansión observada) y un mapa derivado de un modelo (v.g., la expansión simulada). Cuando el índice de Jaccard es 1.0 significa que existe total igualdad y cuando es 0.0 significa que hay total desigualdad. Dado que ambos indicadores son similares, la literatura en inteligencia artificial, específicamente en segmentación de imágenes, recomienda utilizar ambos índices para verificar que los dos apunten en el mismo sentido (Kuo et al., 2002).
La interpretación de los índices Kappa de Cohen y Jaccard se muestra en el Cuadro 1. Éstos son los umbrales más utilizados en la literatura; sin embargo, no dejan de ser arbitrarios. Algo similar ocurre con el coeficiente de correlación de Pearson (Field, 2009) y con muchos otros umbrales utilizados en estadística y en el análisis urbano.
Cuadro 1 Interpretación del Índice de Kappa de Cohen e Índice de Jaccard según umbral
Umbrales del índice Kappa de Cohen |
Interpretación de coincidencia entre imágenes según umbral |
Umbrales del índice de Jaccard |
Interpretación de coincidencia entre imágenes según umbral |
0.00-0.20 |
Baja |
0.00-0.40 |
Baja |
0.21-0.40 |
Regular |
0.41-0.49 |
Regular |
0.41-0.60 |
Buena |
0.50-0.70 |
Buena |
0.61-0.80 |
Muy buena |
0.71-0.85 |
Muy buena |
0.81-1.00 |
Excelente |
> 0.85 |
Excelente |
Fuente: Elaboración propia a partir de Lin et al., 2018; Warrens, 2015; Rosebrock, 2016; Mohan y Khan, 2018.
Los objetivos del experimento definirán si la bondad de ajuste global se estima con la entropía de Shannon, si lo que interesa es modelar la dispersión-concentración de las áreas construidas, o con la dimensión fractal, si el propósito es explorar el crecimiento-forma de la mancha urbana (e.g., la expansión de las áreas construidas) o con los dos indicadores si se quieren explorar ambos temas.
Como se mencionó antes, las herramientas de Christaller hacen un barrido completo de las 256 reglas de transición e identifican la regla que mejor replica la expansión de la mancha urbana en el periodo de experimentación (e.g., 2003-2017), por medio del filtro en cascada que proponemos en la Figura 3. En otras palabras, Christaller construye un modelo con cada regla de transición y valora la bondad de ajuste global de cada uno en la primera fase del filtro en cascada. La valoración de la bondad de ajuste global entre las manchas urbanas observadas en 2017 y las simuladas por los modelos se hace mediante comparación directa. Es decir, se estima la entropía de Shannon y la dimensión fractal para el mapa observado en 2017 y se comparan con los que resultan de las manchas urbanas desplegadas por los modelos. El o los modelos que produzcan la menor diferencia son los que mejor simulan la expansión urbana en el periodo de estudio. Si los indicadores de Shannon y Fractal señalan como óptima la misma regla de transición, tendremos un solo modelo. Sin embargo, lo usual es que cada indicador muestre diferentes reglas de transición como óptimas, ya que se enfocan a diferentes aspectos de la mancha urbana. Al final de esta etapa tendremos, normalmente, varios modelos valorados como los más certeros por cada indicador global (cada uno con su propia regla de transición óptima).
Luego, en la segunda etapa de filtrado, se valora la bondad de ajuste local de los modelos que registraron el mejor ajuste global en la primera etapa de filtrado. En esta segunda fase es donde se utilizan los indicadores Kappa de Cohen y Jaccard. Ambos indicadores miden la similitud entre imágenes y varían en un rango de 0.0 a 1.0. Mientras más se acerquen los valores a 0.0, menor la coincidencia entre las imágenes; y conforme se acerquen a 1.0, mayor la similitud.
La comparación directa no se puede aplicar para estimar la bondad de ajuste local, ya que su medición requiere considerar simultáneamente dos imágenes: la observada y la calculada.11 Lo que procede es definir umbrales para los indicadores de Kappa de Cohen y Jaccard, para facilitar la interpretación de sus valores. Los umbrales utilizados los derivamos de la literatura especializada (Cuadro 1). Es recomendable estimar ambos indicadores de bondad de ajuste local para hacer una doble verificación y asegurarse que los dos apuntan en la misma dirección (Rutter, Lagergren y Flores, 2019).
Si los índices de Kappa y Jaccard registran valores aceptables de similitud (véase el Cuadro 1), puede procederse a proyectar la mancha urbana observada con el fin de construir escenarios exploratorios y/o experimentales. En nuestro caso tenemos un alcance hasta los siguientes cinco y catorce años porque los datos que hemos elegido corresponden a un periodo de cinco (para Tijuana y Acapulco) y catorce años (para Toluca). Si los índices de Kappa o Jaccard no registran valores aceptables de similitud, se deben revisar o replantear los modelos (Figura 3). Éste es el segundo y último nivel del filtro en cascada.
2.1. Ciudades seleccionadas para la prueba empírica del método de modelado
Las tres ciudades seleccionadas para someter a prueba nuestro método de modelado registran diferencias notables, lo que las hace buenas candidatas para experimentar modelos de expansión urbana. Tijuana tiene alrededor de 2.0 millones de habitantes en 2019, con una gran cantidad de población flotante no registrada por los censos. Esto genera un patrón de crecimiento donde abundan zonas de viviendas edificadas por inmigrantes de paso a Estados Unidos, que inicialmente se pensaron como temporales, pero que luego se convirtieron en viviendas definitivas con alto grado de precariedad (Garrocho, 2011). Además, tiene restricciones políticas de carácter binacional al crecimiento urbano (v.g., la frontera con Estados Unidos), y de carácter físico ya que limita al oeste con el océano Pacífico. Por su parte, Acapulco (con alrededor de un millón de habitantes en 2019) es uno de los centros turísticos de playa más importantes de México. Limita con el océano Pacífico y su estructura urbana es lineal en gran parte de la ciudad, justo porque las instalaciones turísticas prefieren localizase frente al mar (García, 2017). Finalmente, Toluca es la quinta ciudad más poblada de México (más de 2.2 de millones de habitantes en 2019); ha registrado una expansión muy acelerada en los pasados años, y enfrenta serios problemas en sus sistemas naturales de recarga de agua (Vilchis-Mata, Garrocho-Rangel y Díaz-Delgado, 2018).
3. Resultados del método ACC para modelar la expansión de la mancha urbana con áreas restringidas en tres ciudades mexicanas
En esta sección se muestran los resultados del método de modelación ACC, la forma como distribuye los datos en tiempo y espacio, y la precisión de sus modelos para replicar las manchas urbanas observadas de las ciudades bajo experimentación. Incluimos en el método ACC zonas restringidas a la expansión de la ciudad: calles, parques, áreas naturales protegidas, límites internacionales (la frontera con Estados Unidos, en el caso de Tijuana) o límites naturales (el mar en Acapulco y en Tijuana), entre muchas otras. Esto le da al método ACC un realismo que no habíamos considerado hasta ahora ( Jiménez, Chávez y Garrocho, 2018).
3.1 Construcción de modelos ACC con áreas restringidas para tres ciudades mexicanas
Se conformó una base de datos para incluir zonas restringidas a la expansión urbana en las ciudades bajo experimentación. Estas restricciones se derivan de información urbanística (e.g., plazas, espacios simbólicos, vialidades), física (e.g., áreas vulnerables, costas o áreas con demasiada pendiente), política (e.g., fronteras internacionales), ambiental (e.g., áreas protegidas), que se emplearon para restringir la expansión urbana. Las variables restrictivas a la expansión se normalizaron, de tal manera que todas responden a una escala de valores que pueden ser 0.0 (i.e., espacio totalmente abierto a la expansión de la ciudad o vacío) y 1.0 (i.e., espacio construido o espacio totalmente restringido a la expansión). De tal manera que se dispone de una imagen para representar el espacio construido y otra para indicar las zonas restringidas.
Prácticamente la mayor parte de la información que utilizamos en este ejercicio para marcar restricciones en las zonas está disponible en la página web del INEGI. Inicialmente, los datos incluidos en los mapas están en formato vectorial, pero se le da un tratamiento a cada imagen y se obtiene un mapa en base tipo raster. Cada una de las categorías de restricciones anteriormente mencionadas es una capa del mapa final, donde se combinan todos los impedimentos para construir o urbanizar. Los mapas fuente de cada ciudad son imágenes satelitales pancromáticas (del satélite Landsat 7 y 8), tomando sólo las bandas 4, 6 y 7, que muestran la superficie con características urbanas en escala de imágenes RGB 7 denominadas falso color (Romano, 2018). El resultado son las imágenes que Christaller utiliza como datos de entrada. Con la imagen del tiempo t se aplican las reglas de vecindad y transición de los ACC, así como las variables de restricción para replicar la expansión urbana de las ciudades bajo experimentación.12 Vale subrayar que todo el proceso de construcción, simulación, valoración y despliegue de resultados de los modelos ACC con restricciones, se realiza de forma automatizada con las herramientas desarrolladas en Christaller.
3.1.1 Modelos ACC y resultados
La primera ciudad bajo experimentación es Tijuana (Figura 4). En 2017 tenía alrededor de 1.9 millones de habitantes. Su área urbana en 2013 cubría 1687 hectáreas y 2 227 en 2017. Esto significa que en el periodo de estudio la ciudad se expandió 540 hectáreas, igual a 32% de la mancha urbana en 2013. Tijuana resulta muy interesante para este trabajo porque tiene importantes restricciones a la expansión urbana: limita al norte con la frontera con Estados Unidos y al oeste con el océano Pacífico. En la Figura 4a se presentan en negro las zonas de suelo ocupado. Esta imagen corresponde a Tijuana en 2013 y es el mapa de entrada (t) para la construcción de los modelos de expansión urbana.

Fuente: Elaboración propia con base en los resultados de las herramientas de Christaller.
Figura 4 Tijuana: mancha urbana con áreas restringidas a la urbanización. Mancha urbana observada 2013 (a) y 2017 (b). Mancha urbana simulada aplicando el filtro de entropíade Shannon 2017 (c) y el filtro de la dimension fractal (d)
Las Figuras 4a y 4b muestran la mancha urbana observada de Tijuana en 2013 y 2017, respectivamente. Por su parte, en la Figura 4c se observa la simulación que se hace a través de las herramientas de Christaller de la expansión urbana de Tijuana para 2017 con la regla más precisa que detectó el filtro de entropía de Shannon: la 91. Lo compacto/ disperso de Tijuana según la entropía de Shannon es prácticamente igual en la imagen observada y en la estimada (para el periodo de cinco años). La diferencia es apenas de tres diezmilésimas. La Figura 4d muestra la simulación de la expansión de Tijuana operando el filtro de la dimensión fractal, que identificó la regla 236 como la que genera la simulación más precisa en terminus de forma/ crecimiento. El resultado también es muy estimulante: la diferencia absoluta fue una centésima (menos de seis décimas de punto porcentual).
Los indicadores de la bondad de ajuste local para Tijuana fueron muy buenos y excelentes (Cuadro 3). Los valores más altos de la bondad de ajuste local se obtuvieron con el modelo que se apoya en la dimensión fractal: Kappa de Cohen = 0.85, y Jaccard = 88.
Cuadro 3 Bondad de ajuste en la segunda etapa del filtrado en cascada: indicadores Kappa de Cohen y Jaccard para las ciudades bajo experimentación, 2017
Entropía de Shannon |
||||
Diferencia |
||||
Ciudad |
Observada |
Calculada |
Absoluta |
% |
Toluca |
0.8162 |
0.9431 |
0.0269 |
2.94 |
Tijuana |
0.8713 |
0.8716 |
0.003 |
0.03 |
Acapulco |
0.4910 |
0.4911 |
0.0001 |
0.02 |
Dimensión fractal |
||||
Diferencia |
||||
Ciudad |
Observada |
Calculada |
Absoluta |
% |
Toluca |
1.83 |
1.84 |
0.01 |
0.55 |
Tijuana |
1.75 |
1.76 |
0.01 |
0.57 |
Acapulco |
1.66 |
1.67 |
0.01 |
0.60 |
Fuente: Elaboración propia con base en los resultados de Christaller.
La segunda ciudad bajo análisis es Acapulco (Figura 5). Se ubica en el estado de Guerrero, en la costa sur de México, y es la mayor ciudad de la entidad. Su población en 2017 oscilaba alrededor de 900 mil habitantes. El área urbana en 2013 cubría 556 hectáreas (Figura 5a) y en 2017 se extendía sobre 662 hectáreas: un aumento relativo de 19.1% (Figura 5b). Es la menor de las ciudades que incluimos en el experimento, pero tiene una característica muy relevante para este trabajo: debido a que es un destino turístico de playa, sigue una estructura que en gran parte es lineal a lo largo del océano Pacífico, muy distinta a las estructuras de Toluca y Tijuana. Por lo tanto, es una buena prueba para el método de modelado ACC.
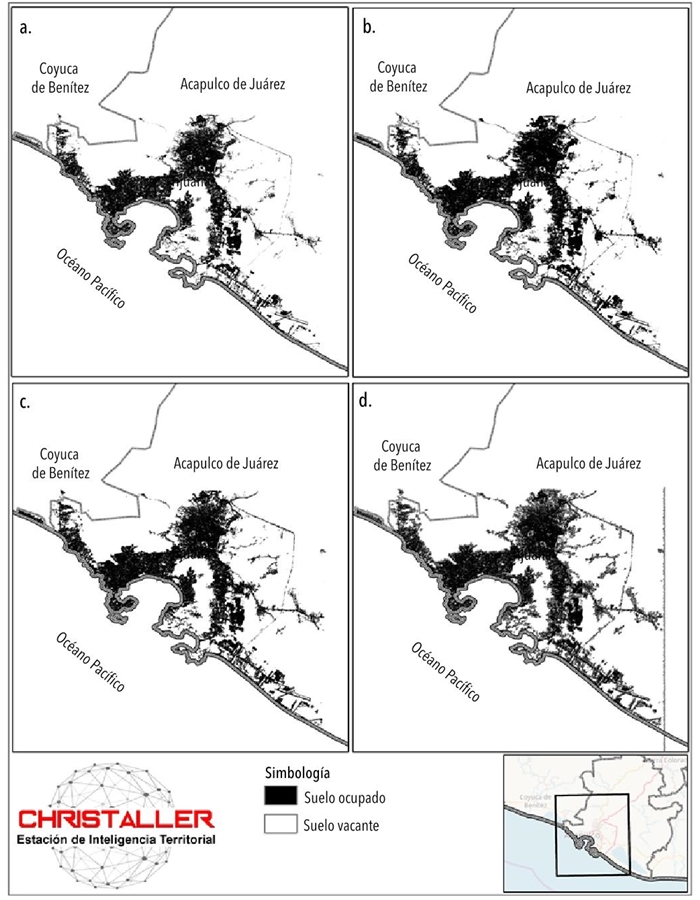
Figura 5 Acapulco: mancha urbana con áreas restringidas a la urbanización. Mancha urbana observada 2013 (a) y 2017 (b). Mancha urbana simulada aplicando el filtro de entropía de Shannon 2017 (c) y el filtro de la dimensión fractal 2017 (d)
Las Figuras 5a y 5b muestran la mancha urbana observada de Acapulco en 2013 y 2017. La Figura 5c muestra la simulación de la mancha urbana con restricciones para 2017 con el filtro de entropía de Shannon aplicando la mejor regla identificada: la 206. Finalmente, la Figura 5d es la imagen de la simulación de Acapulco con restricciones para 2017 operando el filtro de dimensión fractal y la regla de transición más precisa que detectó Christaller: la 47.
Los indicadores de bondad de ajuste global son motivantes. El mejor modelo logró reproducir lo compacto/ disperso (entropía de Shannon) de la mancha urbana observada de Acapulco en 2017 con un error de apenas una diezmilésima, y su crecimiento/ forma con una desviación de poco más de medio punto porcentual. Por su parte, todos los indicadores de bondad de ajuste local fueron excelentes ya que variaron entre 0.84 (Kappa de Cohen) y 0.95 (Jaccard). Los valores más altos se lograron con el filtro de la entropía de Shannon.
La tercera ciudad bajo experimentación es Toluca (alrededor de 2.1 millones de habitantes en 2017). Las Figuras 6a y 6b muestran la mancha urbana de Toluca en 2003 y 2017, respectivamente. El mapa de 2003 es el mapa base (t) y es la entrada de información a los modelos ACC en Christaller. En 2003 la mancha urbana tenía un área de 1 104 hectáreas y en 2017 de 1 831 hectáreas. El crecimiento de la mancha urbana en esos catorce años fue de 726 hectáreas, equivalente a 68% de la superficie inicial.
Las restricciones que le impusimos a la expansión urbana de Toluca también corresponden a 2017 y se muestran en color blanco en la Figura 6. En esta figura no son perceptibles en medio impreso todas las zonas restringidas en las cuales no se puede construir, por lo que daremos algunos ejemplos. Una zona restringida está cerca del centro tradicional de Toluca, que es el área del Cerro de la Teresona (Figura 6a). La pendiente de esta zona hace muy complicada la urbanización, además de que existen restricciones de orden normativo (e.g., protección civil). Otra zona restringida es la del volcán (i.e., el Nevado de Toluca), que está en la parte inferior izquierda de la imagen (Figura 6a). Esta área es parque nacional y ahí no está permitido construir. Una tercera zona importante restringida a la urbanización es la que se localiza en el área de Lerma, al este de la ciudad, ya que tiene terrenos destinados a la expansión del Aeropuerto Internacional de Toluca (Figura 6a).

Fuente: Elaboración propia con base en los resultados de las herramientas de Christaller.
Figura 6 Toluca: mancha urbana con áreas restringidas a la urbanización. Mancha urbana observada 2003 (a) y 2017 (b). Mancha urbana simulada aplicando el filtro de entropía de Shannon 2017 (c) y el filtro de la dimensión fractal 2017 (d)
En la Figura 6b se muestra la mancha observada de Toluca en 2017 y en la Figura 6c la proyección de Toluca para 2017, utilizando el filtro de entropía de Shannon, que detectó que la mejor regla de transición fue la 211. En la Figura 6d se muestra el resultado de aplicar el filtro de dimensión fractal, que encontró que la mejor regla es la 223. Los valores de los indicadores de bondad de ajuste global se presentan en el Cuadro 2.
Cuadro 2 Bondad de ajuste en la primera etapadel filtrado en cascada: entropía de Shannon y dimensión fractal para las ciudades bajo experimentación, 2017
Filtro |
|||
Ciudad |
Indicador |
Entropía de Shannon |
Dimensión fractal |
Toluca |
Kappa |
0.61 |
0.57 |
Jaccard |
0.72 |
0.62 |
|
Tijuana |
Kappa |
0.78 |
0.85 |
Jaccard |
0.83 |
0.88 |
|
Acapulco |
Kappa |
0.84 |
0.92 |
Jaccard |
0.95 |
0.92 |
|
Fuente: Elaboración propia con base en los resultados obtenidos al aplicar las herramientas desarrolladas en Christaller.
Los indicadores de bondad de ajuste global de la entropía de Shannon y de la dimensión fractal para Toluca muestran valores muy alentadores. En el primer caso, la diferencia absoluta es de menos de tres centésimas (la diferencia relativa es la misma porque la entropía de Shannon varía de 0.0 a 1.0). Es decir, el modelo se “equivoca” en menos de tres por ciento al simular lo compacto/ disperso de la mancha urbana de 2003 a 2017. Por su parte, los valores de la dimensión fractal de la mancha urbana observada y simulada difieren en la determinación de su forma/ crecimiento en una centésima en términos absolutos, que equivale a un diferendo relativo de menos de un punto porcentual (el doble de la entropía de Shannon porque el rango de variación de la dimensión fractal es del doble). Hasta aquí todo va bien.
En cuanto a los indicadores de bondad de ajuste local (Cuadro 3), todos van de buenos a muy buenos (véanse los umbrales interpretativos en el Cuadro 1), tanto si los estimamos para el mejor modelo según el filtro de entropía de Shannon, como si lo hacemos para el más preciso de acuerdo al filtro de la dimensión fractal. Debe subrayarse que no logramos indicadores de bondad de ajuste excelentes, quizá por la expansión tan acelerada de Toluca en el periodo de estudio y porque modelamos la expansión durante catorce años y no durante cinco, como en Tijuana y Acapulco. Éstas son hipótesis cuya comprobación está más allá de los alcances de este trabajo. De cualquier manera, los indicadores de bondad de ajuste local son muy satisfactorios, especialmente con el filtro de entropía de Shannon.
Llama la atención la elevada precisión de los modelos y su mejor desempeño en ciudades con velocidades de expansión más lenta y con mayores restricciones a la expansión de la ciudad (Tijuana y Acapulco). El hecho de que el modelo replicó menos bien el crecimiento de Toluca, podría sugerir la necesidad de incluir más información estadística e intuitiva (e.g., humanware) a las células (bits) que integran las imágenes. Ambas hipótesis están fuera de los alcances de este texto, pero deberán probarse en próximos trabajos.
4. Proyección de la mancha urbana de Toluca para 2031
Los valores de los índices de bondad de ajuste ofrecen cierta confianza de que es posible explorar escenarios, más o menos realistas, de la expansión de la mancha urbana de las ciudades bajo experimentación. Por razones de brevedad exploramos un escenario a 2031 para una sola ciudad: Toluca. Esta urbe registró los indicadores de bondad de ajuste menos buenos, pero aun así muy satisfactorios y es la que más hemos investigado los autores de este trabajo. La proyección es para 2031 porque el modelo se calibró con información cartográfica de un periodo de catorce años. Aquí aplicamos el modelo que generó los mejores ajustes en la sección anterior (Cuadro 3). Por tanto, el resultado de la proyección es una mancha urbana probable o condicionada del AMT para 2031. No sobra subrayar: el modelo es, simplemente, un instrumento de planeación que permite generar escenarios razonables de expansión de la ciudad para apoyar la toma de decisiones urbanas y explorar ex ante algunos de sus probables impactos.
En la proyección de Toluca añadimos a las restricciones de expansión de la sección anterior (e.g., vialidades, parques, plazas), otras restricciones estratégicas para el futuro de la ciudad: zonas donde no debe crecer por razones de seguridad hídrica. Esto implicó afinar la consideración del uso del suelo (e.g., agrícola de temporal-humedal), clasificar la vegetación de acuerdo a sus variantes en la cobertura del territorio (e.g., pastizales y bosques, que favorecen la infiltración de agua) y considerar los cuerpos de agua y las áreas claves de recarga de acuíferos (véanse los detalles en Vilchis-Mata, Garrocho-Rangel y Díaz-Delgado, 2018).
Resulta inquietante que muchas de las zonas estratégicas de seguridad hídrica de Toluca son altamente susceptibles a la urbanización por su valor comercial y podría ser que fueran rápidamente ocupadas en una proyección tendencial sin restricciones hídricas. Esto es inaceptable para el futuro de la ciudad. Las zonas estratégicas en materia de seguridad hídrica son vitales para cualquier ciudad y un capital natural muy valioso para Toluca por los servicios ambientales que genera.
La definición de las zonas estratégicas para la seguridad hídrica de Toluca es compleja y no podemos explicarla en este espacio.13 Los municipios de Almoloya de Juárez, Calimaya, Chapultepec, Mexicalcingo, San Antonio la Isla y Santa María Rayón, que son parte del Área Metropolitana de Toluca (AMT), registran mayor dispersión en la construcción de viviendas y cuentan con mayor número de zonas agrícolas que se pueden considerar humedales, pero son muy atractivas para los desarrolladores de vivienda (Figura 7a). Por otro lado, los municipios de Ocoyoacac, Metepec, Toluca y Zinacantepec están en etapa de consolidación en su urbanización y son aún más atractivos para hacer negocios inmobiliarios. La Figura 7b muestra el mapa de las zonas restringidas para el AMT en 2017. Se incluyen restricciones debidas a infraestructura y equipamiento urbano, así como las zonas de alta importancia hídrica.

Fuente: Elaboración propia con base en los resultados de las herramientas de Christaller.
Figura 7 Toluca: mancha urbana, municipios metropolitanos (a) y zonas restringidas a la expansión de la ciuda por su importancia hídrica (b)
Así, los escenarios que vamos a proyectar exploran la siguiente pregunta clave: ¿Cómo sería la expansión probable de Toluca si se respetan o no las zonas estratégicas en materia de seguridad hídrica? La pregunta es compleja y casi imposible de explorar sin contar con un modelo relativamente confiable de expansión urbana.14 El análisis que presentamos es obligadamente sucinto por las limitaciones de espacio y porque se trata sólo de ilustrar una aplicación del modelo. Para abreviar, nos referiremos al escenario en el que no se respetan las zonas estratégicas por su importancia hídrica como el escenario 1 (E1), y al escenario donde sí se respetan las restricciones hídricas como E2.
4.1 Resultados de la exploración de escenarios
En 2017 la zona urbanizada de Toluca cubría 1 831 hectáreas; en la proyección realizada para 2031 se cubren 3 148 hectáreas de suelo urbanizado. Esto implica un aumento de 1 317 hectáreas, lo que significa que en 14 años la ciudad crecería casi 80% con respecto a 2017. El crecimiento de los catorce años previos (de 2003 a 2017) fue 68% (véase la sección 3). La proyección del modelo parece implicar una expansión más acelerada, lo que va a contracorriente de lo que reporta la literatura mexicana para las grandes ciudades de México (Garrocho, 2013). Sin embargo, la explicación es otra: Toluca está rodeada de asentamientos que hoy están aislados de la mancha urbana, y su expansión los incorporaría al área urbana continua, lo que incrementará notablemente su extensión. Éste sería un primer hallazgo.
En el E1 destacamos cuatro zonas que registran expansión urbana (Figura 8): una concentrada en la periferia del noroeste de la ciudad (en Almoloya de Juárez, espacio rico en tierras agrícolas), otra que forma una franja en el oeste (en Zinacantepec, municipio consolidado), una más que se aglutina en el extremo este (en Lerma), y finalmente una en el sureste de la mancha urbana (al sur de Metepec, Mexicaltzingo y Calimaya, áreas ricas en tierras agrícolas). En el E1 no sólo se pierden zonas agrícolas claves, sino que se afectan áreas hídricas de importancia estratégica, especialmente en Almoloya de Juárez y Zinacantepec; en un eje que corre del centro al noreste donde se pierden tres áreas completas en diversas áreas de Lerma y San Mateo Atenco; y algunas otras en Metepec y Mexicaltzingo (Figura 8a). El contraste es muy interesante si comparamos estas zonas de la Figura 8a con lo que ocurre en la Figura 8b, que representa el E2. Puede llamar la atención que se detectan zonas restringidas que registran cierta expansión urbana. La razón es que ya registraban expansión en 2017 y la proyección contempla la inercia que genera ese crecimiento.
5. Conclusiones, aportaciones y agenda de investigación
Este trabajo interdisciplinario (combina geografía urbana, matemáticas para sistemas dinámicos, alta tecnología y ciencias computacionales) presenta una metodología genérica que permite construir en poco tiempo modelos operativos específicos de la expansión de ciudades mexicanas. Nuestra metodología, que llamamos Autómatas Celulares en Cascada (ACC), está automatizada en la Estación de Inteligencia Territorial Christaller de El Colegio Mexiquense.
5.1 Conclusiones
Los modelos que construimos consideran diversas restricciones al crecimiento físico de la ciudad (e.g., calles, espacios públicos, áreas no urbanizables por normatividad, por razones ambientales o por límites político-administrativos, entre muchas otras). Sometimos nuestra metodología a una triple prueba empírica. Medimos su capacidad para generar modelos de simulación de la expansión urbana para tres ciudades con características contrastantes: las áreas metropolitanas de Tijuana, Acapulco y Toluca. Utilizamos mapas raster con un muy alto grado de resolución: 15 x 15 metros. Valoramos la bondad de ajuste entre las simulaciones de los modelos construidos con nuestro método y la expansión urbana observada. Consideramos el periodo 2013-2017 para Tijuana y Acapulco y 2003-2017 para Toluca porque contamos con datos e imágenes confiables para esos años. Utilizamos indicadores de bondad de ajuste global y local entre imágenes (v.g., mapas), articulados en un filtro en cascada, que permite reducir los tiempos de procesamiento computacional de manera notable. Construir el modelo óptimo para cada ciudad bajo experimentación tomó, en promedio, poco menos de cuatro horas de procesamiento de cómputo. Los resultados de las simulaciones fueron muy alentadores. Finalmente, ilustramos cómo nuestra aproximación metodológica puede alimentar políticas urbanas relacionadas con la expansión de las ciudades, para avanzar hacia el codiseño de políticas urbanas.
5.2 Aportaciones
El trabajo presenta aportaciones metodológicas y empíricas de alta aplicabilidad al análisis y planeación de las ciudades en México. Primero, incorporamos áreas restringidas al crecimiento urbano (e.g., calles, espacios públicos, zonas estratégicas por su importancia ambiental, áreas de alto riesgo, fronteras internacionales, costas) en la construcción de modelos de expansión urbana basados en autómatas celulares, lo que permite construir escenarios más realistas sobre la expansión de las ciudades. Segundo, nuestros modelos permiten modelar la aparición de nuevas áreas urbanizadas dispersas. Tercero, la aplicación de las reglas de transición inicia en puntos de las ciudades seleccionados de manera aleatoria, lo que reduce notablemente el determinismo de los modelos. Cuarto, nuestros modelos se fundamentan en la búsqueda exhaustiva de la o las reglas de transición que ofrecen la mejor bondad de ajuste entre la expansión calculada y la expansión observada. Finalmente, la quinta aportación, quizá la más importante en términos metodológicos, es el filtro en cascada, que permite apoyar indicadores de bondad de ajuste locales sobre la base de indicadores globales, lo que redujo en más de 50% el tiempo de procesamiento computacional, sin menoscabo de la calidad de los resultados. Esto es clave si se trata de construir modelos urbanos interactivos que, apoyados en herramientas de frontera, apoyen procesos colectivos de consulta y codiseño de decisiones urbanas.15
En términos empíricos, las aportaciones también son diversas: se construyeron modelos de expansión urbana restringida, con muy buenos indicadores de bondad de ajuste globales y locales, para tres ciudades de características contrastantes. Estos modelos están disponibles en código abierto y sin costo en la Estación de Inteligencia Territorial de El Colegio Mexiquense (http://www.christaller.org.mx/). Lo mismo ocurre con nuestro método de modelado ACC, que puede aplicarse a cualquier ciudad de México y de otros países latinoamericanos y generar modelos específicos. Además, se mostraron algunos de los impactos más notables de la expansión urbana de la Zona Metropolitana de Toluca en caso de que no se protejan sus áreas estratégicas por su importancia hídrica.
Estas aportaciones sientan bases para apoyar en México la construcción de modelos interactivos de simulación de la expansión urbana, acordes a la disponibilidad de información y capacidad financiera de nuestras ciudades, que vinculen software, hardware y humanware en ambiente SIG.
5.3 Agenda de investigación
Este trabajo abre una apasionante agenda de investigación para lograr modelos urbanos apoyados en herramientas de frontera y en la sensibilidad y conocimiento de los ciudadanos. Todo con el fin de ampliar los límites del conocimiento de nuestras ciudades y apoyar procesos colectivos de consulta y codiseño de decisiones urbanas, especialmente en el ámbito local.16
Para lograrlo, se requiere adoptar una perspectiva tipo cyborg, que combine conocimiento, métodos y tecnologías de frontera con la inteligencia y sensibilidad de la población que vive y trabaja en las ciudades. Por tanto, requerimos modelos sencillos de entender (aunque su diseño sea complejo) y operar (lo que implica avances sustantivos en la conexión transparente de software y SIG), que necesiten relativamente poca información (acordes a la limitada capacidad financiera de los gobiernos locales), capaces de incorporar información especializada de fuentes e informantes no tradicionales en la construcción de modelos urbanos. Nos referimos a información cualitativa/ subjetiva y cuantitativa de gran utilidad: niveles de tráfico en los espacios intraurbanos (que pueden reportar taxistas y repartidores de ruta, o tomarse de aplicaciones disponibles sin costo, como Waze), tendencias de las preferencias de los compradores de vivienda por ciertas zonas de la ciudad (mediante informes de agentes de bienes raíces, de las bases de catastro, de los permisos de construcción y de información dispersa en internet sobre tendencias de localización de negocios, por ejemplo), niveles de seguridad pública (a partir de bases de datos georreferenciados de cuerpos de seguridad), grandes proyectos inmobiliarios o comerciales que están en cartera en la ciudad (información no publicada que pueden aportar desarrolladores inmobiliarios clave, cámaras empresariales, funcionarios públicos). Éstos son sólo algunos ejemplos de la información que deben incorporar los modelos operativos de expansion urbana que requiere el codiseño de ciudades sostenibles de México en el siglo XXI.
Todo esto va a requerir nuevo conocimiento, métodos y herramientas. Destacamos cuatro campos centrales: I. Big data, para analizar grandes volúmenes de datos y extraer información factual y subyacente, disponible pero no aprovechada cabalmente por los analistas urbanos (e.g., económica, topográfica, cambios de densidad de población y por tipo de empleo, tendencias del mercado inmobiliario, probabilidades percibidas de crecimiento en el territorio, intensidad de tráfico vehicular); II. Inteligencia artificial (AI), especialmente en el tema de evaluación multicriterio de políticas urbanas públicas y privadas (e.g., para seleccionar las opciones más convenientes para el desarrollo urbano sostenible o hacer las valoraciones de grandes proyectos en términos de la sostenibilidad de la ciudad); III. Aprendizaje automatizado o Machine Learning, que es una rama de la AI para convertir muestras de datos en programas de computadora de manera más rápida y eficiente, con el fin de develar el comportamiento de conjuntos de datos más amplios (e.g., el comportamiento espacial de la población que vive y trabaja en las ciudades: localización residencial, comercial, industrial, de grandes proyectos, flujos de población y bienes en el espacio intraurbano; zonas atractoras/ expulsoras de población y empleo); y IV. Elemento crisol, un equipo de investigación interdisciplinario y plural que debe sintetizar lo anterior, no sólo para lograr mejores simulaciones y construcción de escenarios sobre la expansión de las ciudades, sino para generar nuevo conocimiento sobre nuestras ciudades a partir de la experimentación que permiten los buenos modelos de expansión urbana. Este cuarto elemento es el fin y el inicio de un proceso circular y acumulativo de mejora continua en términos científicos, operativos y democráticos para el codiseño de las ciudades.











 nova página do texto(beta)
nova página do texto(beta)





