Distinguir entre la expresión y la estructura de una demostración puede permitir disolver algunas confusiones filosóficas. Por ejemplo, evitar el error de trasladar (de manera inadvertida y acrítica) propiedades de la expresión o comunicación de la prueba a su estructura; quizá el caso más notable de tal ejercicio de contrabando intelectual sea la adopción de la exigencia de finitud para la demostración (qua estructura), con base en la obvia finitud de la demostración (qua expresión).1 Ahora bien, una vez advertidos de la distinción entre la estructura y la expresión, otros fenómenos previamente invisibles surgen en nuestro horizonte intelectual. Así, dos demostraciones pueden tener la misma estructura y su comunicación puede presentar diferencias; casos triviales son la expresión de la demostración mediante idiomas distintos o con notaciones irrelevantemente diversas de las constantes lógicas. Además de situaciones nada interesantes como éstas, hay otras que merecen una atención reflexiva. Por ejemplo, cuando exponemos una demostración (y, en general, un argumento cualquiera) solemos adaptar el estilo al receptor y a nuestros propósitos. En relación con la demostración matemática, Chateaubriand señala específicamente:
Las demostraciones son parte de la actividad de las matemáticas; sirven para establecer resultados y para que la gente vea la configuración del terreno. Los recursos que se utilizan en las pruebas dependen mucho de la audiencia y del propósito de las demostraciones, pero generalmente son mucho más variados de los que se encapsulan en las demostraciones idealizadas de una teoría de la prueba. (Chateaubriand 2005, p. 305; las cursivas son mías.)
Más aún, la modalidad o el formato de la comunicación (entendiéndola como parte de los “recursos” que se señalan en la cita precedente) puede variar dependiendo del receptor y/o de los propósitos del agente matemático. Podemos dedicar atención a estas alteraciones adoptando como unidad de análisis la totalidad de la demostración.2 Pero hay asimismo una variante en la apreciación de este fenómeno que surge al privilegiar como unidad de análisis los distintos “momentos” o “etapas” de la demostración. Es decir, podemos intentar analizar los formatos o los estilos comunicacionales (resultantes de la consideración del destinatario o de los propósitos del agente) correspondientes a dichos “momentos” expresivos. Luego, obtendríamos información relevante del, por así denominarlo, “estilo comunicacional” de la demostración considerada en su sentido global como combinación de aquellos modos o formas comunicacionales. Aunque estos formatos de los diversos tramos de una demostración singular pueden diferir en dimensiones distintas, me interesa estudiar aquí un caso particular, a saber, cuando la diferencia reside en el grado de explicitación descriptiva de la correspondiente estructura deductiva.3 Dicho de otra forma, me interesa explorar las razones que subyacen en la diversificación intencionada (en la comunicación de una demostración singular) de formas expresivas que contrastan en términos de su diferente nivel de explicitud en la descripción de los respectivos tramos deductivos. Como se sigue de esta caracterización, el nivel de explicitud no es meramente una cuestión de detalle expositivo, pues se trata de qué se describe y qué se omite (total o parcialmente) de la estructura de la demostración. En consecuencia, el talante expresivo posee un calado estructural relevante. Para simplificar la exposición, denominemos polimodal al estilo, a la expresión, a la comunicación (de la demostración matemática) que posea este rasgo.
¿Es este estilo una rareza? No lo creo. Si estoy, por ejemplo, explicando una demostración a mis estudiantes en clase, quizá opte por concentrarme en los pasajes que pienso que les pueden resultar más difíciles y me permita una referencia rápida a aquellos con un grado menor de dificultad. o, si se trata de una comunicación a colegas en un congreso, tal vez privilegie los trechos que considero relevantes y novedosos, despreocupándome de los menos creativos. En cualquier caso, la administración de las variadas modalidades expresivas es un recurso expositivo ordinario para comunicar una demostración; los motivos para usar tal expediente no se limitan, por supuesto, a los ejemplos que ofrezco aquí.
Ahora bien, encontrar entonces que Euclides se sirva de un estilo polimodal en sus Elementos no debiera resultar sorprendente -dada la relativa informalidad de su práctica deductiva-. Pero, ¿cuál podría ser la racionalidad subyacente en el uso de tal recurso representacional? o, habida cuenta de la decisiva interacción entre la estructura y la expresión, ¿cuál es la lógica explicativa de esa dinámica expresiva? Razonar sobre estas interrogantes, y específicamente en el contexto de la demostración euclidiana, es el objeto de este artículo.4
El itinerario expositivo será el siguiente. En el apartado 1 caracterizo y ejemplifico el estilo polimodal de la demostración euclídea. En el apartado 2 ofrezco un nuevo ejemplo cuya única novedad reside en que se trata de una apelación a una polimodalidad relativamente más sofisticada, pues introduce la característica heterogeneidad inferencial de la demostración euclídea.5 En el apartado siguiente, ofrezco una conjetura inicial (inspirada en los casos estudiados antes) acerca de la racionalidad que subyace en la polimodalidad: la motivación estético/pedagógica. En el apartado 4 estudio una clase de demostraciones polimodales euclidianas radicalmente novedosa; tales demostraciones (que se encuentran en los libros I y III de los Elementos) revelan una suerte de patrón argumental común. En el apartado siguiente muestro cómo las demostraciones de este tipo obligan a una relativización de la hipótesis original: en ellas la estructura determina la expresión y luego la motivación principal ya no puede ser estético/pedagógica, sino que es de naturaleza estructural o lógica -en sentido lato-. El apartado 6 expone el contraste entre los dos tipos de discurso polimodal que he identificado, respectivamente, en las pruebas que se examinan en los apartados 1, 2 y 3. Por último, dedico un apartado para una módica reflexión metodológica acerca del uso de la distinción a la expresión y la estructura.
1
Empecemos por intentar describir (en forma detallada) cómo se manifiesta, en el caso particular de los Elementos, el fenómeno polimodal. Ciertas demostraciones en Euclides requieren el tratamiento de múltiples casos. Por ejemplo, el caso de los ángulos α y β y el caso de los ángulos δ y γ. La inferencia (a los efectos de la exhaustividad que se exige estructuralmente) debe entonces tratar ambas alternativas. Sin embargo, en la comunicación de la demostración uno de los casos (por ejemplo, el que corresponde a α y β) se trata en forma detallada, morosamente, y el otro (el caso de los ángulos δ y γ) es descrito en forma general -con indicaciones acerca de cómo podría tratarse en forma semejante al primer caso-. Dicho de otra forma: podemos distinguir en el estilo polimodal euclidiano, entendidos en forma contextualizada, dos formatos o modalidades expresivas: un formato (contextualmente) preciso y detallado, y un formato (contextualmente) más genérico y aproximado. Esta diversificación expositiva responde, ocasionalmente, a presiones distintas (incluidos, aunque no de manera excluyente, las audiencias y los propósitos). Queda así suficientemente bien caracterizada la forma de la polimodalidad en la demostración euclidiana que me interesa estudiar; cualquier lectora o lector de los Elementos puede identificar en sus demostraciones (con absoluta certeza) los dos tramos o bloques expresivos mencionados. ¿Por qué? Pues porque, en general, Euclides hace todo el trabajo: luego de ofrecer una demostración, nos dice explícitamente que “de manera semejante demostraríamos que” se da tal y tal cosa o emplea formulaciones equivalentes -salvo en ciertos casos obvios-.
Veamos algunos ejemplos. Empecemos justo por los casos obvios, pues configuran una situación especial: en ciertos casos, el texto no se refiere en forma explícita a la ejecución de una parte de la demostración porque, aunque sea esencial en la estructura de la prueba, el receptor o destinatario conoce perfectamente cómo desarrollarla y, eventualmente, el agente posee determinados propósitos que se satisfacen mejor con la simple omisión de la expresión. Es decir, el agente considera que es innecesaria la referencia a la parte (expresivamente) ausente, pero tal ausencia no acarrea un yerro lógico, sino meramente una estrategia expositiva. Se omite decir “puede usted construir la parte restante porque es muy similar a la que desarrollamos aquí”, pero así se interpreta en forma estándar la comunicación. Se trata, podríamos decir, de un “caso límite” del fenómeno que quiero considerar.
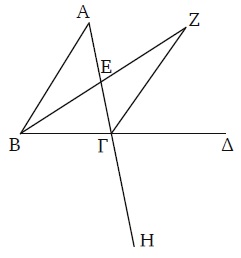
Introduzcamos una notación práctica: designemos con “B1” al bloque o tramo expresivo que representa en forma precisa y detallada la trama inferencial correspondiente, y con “B2” al bloque o tramo expresivo que representa en forma más general y compacta la respectiva trama demostrativa. Si hubiera que retratar ahora el formato expresivo de los casos “límite” referidos antes podríamos hacerlo así: “B 1/B2” -donde “B 1” está en negritas para representar que el bloque correspondiente se encuentra en forma explícita, mientras que el bloque “B2” no se refiere en la expresión de la prueba-. Ilustremos esta situación a través de la demostración de I.6.6
Se trata de una prueba que se estructura como una demostración por absurdo. Luego, se da por supuesta la negación de lo que se pretende demostrar. Como lo que se pretende probar es que los lados (que subtienden ángulos iguales) son iguales, se parte de que son desiguales. Y se razona así:
Pues si AB no es igual a AΓ, uno de ellos es mayor. Sea AB el lado mayor.
Como la lectora, el lector sabe, aquí no hay error lógico. Euclides es perfectamente consciente de que aquello que suponemos al negar la conclusión implica que “uno de ellos es mayor”. La información que provee la suposición se reduce luego a la siguiente disyunción: o bien AB es mayor que AΓ o bien AΓ es mayor que AB. No sabemos que AB es, precisamente, el mayor, pero lo suponemos (sin pérdida lógica) pues la prueba que realizaremos nos permite efectuar una prueba similar o análoga tomando a AΓ como el mayor. No prescindimos estructuralmente de la demostración del caso en que AΓ es el mayor, prescindimos radicalmente de su comunicación -el contraste en términos de explicitación entre los bloques queda captado, como se dijo, a través de representarlo así: B 1/B2-. La misma situación puede ilustrarse si apelamos a I.29.
Por supuesto, la comunicación no siempre puede restringirse a explicitar el tratamiento de uno de los disyuntos. Así, por ejemplo, en I.19 la demostración también es por absurdo; se trata de suponer la negación de que AΓ sea mayor que AB, y luego se tiene que:
o bien AΓ es igual a AB o menor.
Y Euclides demuestra en forma pormenorizada que no es igual, ni es menor, a los efectos de probar el absurdo -es evidente la diferencia (respecto del caso anterior) entre los componentes de la disyunción en este caso: desigualdad e igualdad-. La expresión tratará allí en forma explícita ambas posibilidades por exigencias estructurales. No hay espacio entonces para el recurso a la polimodalidad; usando de una forma algo inapropiada nuestra notación, podríamos decir que ambos tramos expresivos poseen un solo estilo, a saber, B1. Una lección importante de esto nos permite extraer el siguiente contraste: la posibilidad de recurrir al estilo expresivo polimodal depende de las condiciones establecidas por la estructura de la demostración. Las demostraciones de, por ejemplo, I.6 y I.29 permiten tal recurso, no así la de I.19. Estas consideraciones nos recuerdan la articulación decisiva entre la expresión y la estructura y, en particular, la existencia de restricciones a la “libertad expresiva” impuestas por la presión estructural.
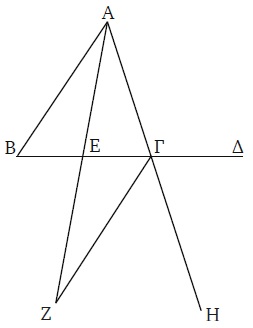
Además de situaciones “límite” como la que ejemplifica I.6, existen casos donde ambos bloques son perfectamente identificables y explícitos y poseen un grado diverso de detalle -luego representamos la situación así: B 1/B 2-. Y ambos bloques desempeñan, por supuesto, un papel esencial en la descripción de la estructura de la demostración. Esto es lo que ocurre en la demostración de I.15. En ella se trata de probar que, si dos rectas se cortan, los ángulos opuestos por el vértice son iguales. La figura es la siguiente:
Una vez que Euclides demuestra que ΓEA es igual a BEΔ, agrega:
de manera semejante demostraríamos que también los ángulos ΓEB, ΔEA son iguales.
Este pasaje se refiere a la compleción de la demostración, y añade información acerca de la estructura de la prueba de esta última igualdad. ¿Cuál es esa información? La analogía o semejanza con la demostración que se acaba de exponer detalladamente. A diferencia del caso límite, aquí se identifica qué resultado se prueba (ΓEB y ΔEA son iguales) mediante la descripción correspondiente y, además, se señala sucintamente cómo se prueba: “de manera semejante” a como se demostró que ΓEA es igual a BEΔ. También las demostraciones de I.17, I.20, II.1, II.8, II.9, III.7, III.8, III.16, IV.2, IV.3 y IV.5 ejemplifican esencialmente la misma situación -aunque existen diversos grados de explicitud en la expresión y complejidad en la estructura inferencial mencionada-.
Estos ejemplos ilustran ya algunos rasgos generales relevantes del fenómeno bajo estudio. En primer lugar, no se trata en estos casos de que la demostración sea omisa o defectuosa en el sentido de que no contempla un caso que debería abordar. No hay un gap en la prueba; no hay un déficit lógico. En segundo lugar, la parte descriptiva de estilo abreviado o general (B2) “completa” la demostración. Si se me permite la metáfora: tal trecho expresivo no es lógicamente ocioso. Luego, se comunica la totalidad de la demostración (qua estructura). Pero, desde el punto de vista expresivo hay, como se dijo, una diferencia notoria: una alternativa se expresa pormenorizadamente y la otra no se expone de igual forma, con el el mismo nivel de detalle. La comunicación, como ya se señaló, refleja las demandas estructurales; más aún, en estos últimos casos, las identifica y agrega información sobre cómo atenderlas. En un sentido epistémico, la prueba es exhaustiva, completa. La diferencia se ubica luego en el plano expresivo: el estilo expresivo del primer tramo es detallado, el de este segundo tramo es sintético o abreviado -sin embargo, repárese en que se trata siempre de descripciones de la estructura deductiva-. Si se nos propusiera, además de esta comunicación compacta, una comunicación desarrollada en forma circunstanciada, con el mismo nivel de explicitud, podríamos afirmar (en forma perfectamente inteligible) que tenemos, en efecto, dos comunicaciones diferentes, pero de la misma estructura deductiva. En tercer lugar, la articulación entre ambos formatos es, en general, estable: primero se presenta la exposición pormenorizada y luego la sucinta. La razón del orden que efectivamente se constata en Euclides es obvia: la segunda se sirve de la primera para efectos comunicativos. Podríamos decir que la última (B2) se “ahorra” información esencial contenida en la primera (B1).
2
Aunque el estilo polimodal sea esencialmente el mismo, pueden existir grados de explicitud diversos. Examinemos un ejemplo más para ilustrar esta idea.
En I.16 debe demostrarse que, dado un triángulo, “si se prolonga uno de sus lados, el ángulo externo es mayor que cada uno de los ángulos internos y opuestos”. La figura es ésta:
Luego de demostrar que AΓΔ es mayor que BAE, leemos en Euclides lo siguiente:
Así pues, de manera semejante, si se divide en dos la recta BΓ, se demostrará que también el ángulo BΓH, es decir el ángulo AΓΔ (I.15), es mayor que el ángulo ABΓ.
Esta descripción posee las características de generalidad (B 2) que contrastan con los rasgos de especificación propios del formato comunicacional precedente en esta prueba (B 1). Se trata sin duda de un ejemplo de expresión polimodal. Pero esta B 2, si se la compara con sus análogas de las ilustraciones inmediatamente precedentes, ofrece una dosis informativa significativamente mayor. Quizá la novedad más obvia resida en que no se usa la misma figura; es necesario construir una nueva. Al indicar la necesidad de dividir en dos segmentos iguales BΓ, el texto no deja la menor duda acerca de la pertinencia de la nueva construcción. Al mismo tiempo ofrece indicaciones precisas sobre cómo resolver el paso fundamental, indicando el foco a atender en el diagrama descrito (BΓH) y señalando cuál debe ser la justificación lingüística correspondiente en la trama demostrativa referida (I.15). El diagrama anunciado obviamente puede ser el que muestra la Figura 3.
Se advierte entonces un uso del recurso lingüístico (en B 2) extremadamente original: no supone éste, como es frecuente, “reinterpretar” o “desambiguar” la figura en cuestión, en este caso la Figura 2 (tal tratamiento estándar, por ejemplo, puede verse en la demostración de II.4), sino que guía la producción del diagrama que debe usarse (Figura 3).7
Dicho de otra forma: B 2 no sólo interviene en forma decisiva en la recepción o decodificación del diagrama, sino que “dirige” lingüísticamente un proceso constructivo o productivo de la figura. La demostración descrita en B 2 posee (así como B 1) una naturaleza heterogénea (es decir, combina en una forma inferencial relevante los componentes expresivos lingüísticos y visuales), pero provee diversa información lingüísticamente codificada y, vía lingüística (a diferencia de B 1), se instruye acerca de la construcción de la fuente de información gráfica que interactúa en la demostración correspondiente (en forma similar a B 1). otro ejemplo de esta naturaleza es la demostración de III.2. Como se señaló antes, en la expresión polimodal aparece primero un formato más detallado (B 1) y luego se apela a una descripción más general (B 2). Si se observa esta variación de formatos no ya en cuanto a su contraste estilístico respecto a la descripción estructural, sino concentrándonos exclusivamente en el plano expresivo, la diferencia de grado de explicitación consignada se manifiesta en un contraste cualitativo. En general, mientras que B 1 describe construcciones e inferencias propias de la teoría y constitutivas de la prueba, B 2 parece situarse (al menos parcialmente) en un nivel meta: se habla (esencialmente) de la estrategia expuesta en B 1. Podría decirse que se trata (parcialmente) de un discurso sobre o acerca de dicho bloque. más aún: tal discurso (B 2) no sólo ilumina el tramo estructural correspondiente, sino que, en cierta forma, promueve una aprehensión novedosa de la anterior etapa expositiva (B 1). Ésta, inicialmente, expresa en forma exclusiva los movimientos que conforman el pasaje demostrativo correspondiente; pero ahora, además, presta otro servicio, a saber, funciona como ejemplo o paradigma para la compleción inferencial. Tal resignificación de la primera etapa es un producto directo de la acción meta-demostrativa de la etapa segunda.
Este rasgo evidencia que la polimodalidad supone una operación compleja, no reductible a la mera inclusión de un recurso de abreviación o resumen expositivo. En particular, la distingue de estrategias tales como la apelación a resultados previos, pues aquella supone simultáneamente la resignificación o lectura meta de un tramo demostrativo, a la vez que describe un tramo nuevo pero semejante a aquel, en el contexto de una única prueba. Aunque el primer aspecto quizá podría aproximarla al uso de resultados anteriormente obtenidos, el segundo la diferencia en forma neta. Además, hay que agregar en atención a las observaciones previas su fuerte originalidad cuando la demostración descrita contiene una construcción gráfica lingüísticamente orientada.
3
A partir del estudio del conjunto de ejemplos de polimodalidad tratados en 1 y 2, ¿cuál podría ser la motivación para optar por tal estilo expresivo? Una respuesta estrictamente descriptiva podría ser: evitar cierta dosis de redundancia en atención a las capacidades del receptor. Para el destinatario supuesto, una comunicación más extensa es superflua u ociosa; la sucinta es perfectamente eficiente en términos informativos. Ahora bien, cabría luego preguntarse el porqué de la valoración, por parte del agente, de la brevedad, de la economía expresiva, al punto de comprometerse con la aplicación sistemática de un formato comunicacional.
Podrían aventurarse dos conjeturas. La primera: tal secuencia u ordenamiento parece encontrar en la preocupación pedagógica o, más precisamente, didáctica una buena justificación. Se describe con cierto detalle un tratamiento heterogéneo inferencial y luego, aprovechando esa comprensión, se describe en términos más generales cómo podría completarse la demostración. Se fomentaría así la imaginación creativa y la familiaridad del destinatario con la práctica inferencial. Incluso podría sugerirse que esta modalidad comunicativa fortalecería (en el receptor) las capacidades meta-cognitivas en relación con el modo novedoso de apropiarse de la fase primera (B 1) a partir de las exigencias vigentes en la fase segunda (B 2). En tal sentido, mi hipótesis atendería los propósitos del agente y, por supuesto, a las capacidades del receptor. Las virtudes didácticas de los Elementos han sido resaltadas por Vega Reñón; este autor recuerda un pasaje de Proclo:
[E]n todas las ciencias es difícil seleccionar los elementos y disponerlos en su debido orden […] Y de quienes han abordado esta empresa, unos han sido capaces de compilar más proposiciones y otros menos; unos han dado pruebas muy sucintas y otros han dilatado su exposición con interminables minucias[.](Proclo 1970, p. 73; las cursivas son mías.)
Y agrega Vega Reñón:
A la luz de esto podemos apreciar las excelencias del trabajo de Euclides sobre los demás tratados, anteriores o posteriores, de este género. Contamos con razones de dos tipos para acreditarla: una parece ser más bien de carácter disciplinario o didáctico, hacen referencia a las virtudes expositivas e instructivas de la composición euclídea; las otras son más bien de carácter metodológico y guardan relación con la sistematización deductiva de las teorías o cuerpos de conocimiento que contiene. (Vega Reñón 2000, p. 23; las cursivas son mías.)
Aunque el autor piensa que quizá estos dos tipos de razones no fueron perfectamente distinguidos por los griegos, cita un largo pasaje de Proclo especialmente valioso para el aspecto relevante aquí:
Un tratado así ha de verse libre de todo cuanto sea superfluo, pues eso obstaculiza el aprendizaje; debe cribar todo lo comprendido por el objeto de estudio de forma coherente y conducente al fin propuesto, en orden a ser de mayor utilidad para el conocimiento; ha de poner sumo cuidado tanto en la claridad como en la concisión, pues lo contrario entorpece la comprensión[.] (Proclo 1970, p. 73; las cursivas son mías.)
Tales observaciones apuntarían a otorgar verosimilitud histórica a la conjetura sugerida antes. Sin embargo, la observación de Beppo Levi parece apuntar en otra dirección:
Euclides (o Teeteto) no tenía como fin enseñar geometría -para las prácticas geométricas bastaban otros maestros, aquellos que, según dice Sócrates, medían por división-, sino que se dirigía a personas cultas que sabían geometría y a las cuales pretendía mostrar cómo las verdades geométricas se ordenan en el entendimiento. (Levi 2006, p. 92)
Por supuesto, tal vez ambas líneas de pensamiento podrían hacerse compatibles acentuando la comprensión de los resultados, no su mero reconocimiento. Pero, como la lectora o el lector recuerda, mi objetivo es simplemente ofrecer una posibilidad lógica, no una respuesta históricamente rigurosa.
Una segunda conjetura: podría pensarse que ofrecer una expresión económica, estilizada, sin agregados redundantes o superfluos, responde a una preferencia estética del agente, pues ese estilo proveería una demostración más elegante. La asociación de la belleza de una demostración con su brevedad y simplicidad ha sido común. Se lee, por ejemplo, en Rota 2015: “Una prueba que se considera bella suele ser breve” (p. 3). Así lo afirman categóricamente Inglis y Aberdein 2015: “Una visión clásica de la belleza matemática se relaciona con la noción de simplicidad” (p. 89). Y reproducen a continuación el elocuente párrafo de McAllister 2005: “Habitualmente, los matemáticos han considerado bella una prueba si se ajusta a los ideales clásicos de brevedad y sencillez. El determinante más importante de la belleza percibida de una prueba es, por lo tanto, el grado en que se presta a ser captada en un solo acto de aprehensión mental.” (p. 22). Inglis y Aberdein discrepan con tal aserción, pero una vez más debe recordarse que mi modesto esfuerzo consiste en ofrecer apenas posibles motivaciones. En el caso de esta conjetura, como en la opción pedagógica, la elección del estilo expresivo respondería a los propósitos o ideales del agente, así como a las capacidades del receptor.
Conviene anotar que la motivación estética es independiente de la educativa -por ejemplo, podría parecer sin duda más razonable optar por una alternativa exclusivamente estética en los denominados “casos límite”-. No obstante, se entendió que, a los efectos de resaltar la idea central de este artículo, resultaba conveniente agrupar ambas motivaciones dada su obvia compatibilidad y su núcleo común: la opción por la brevedad expositiva, sin pérdida comunicacional matemática. Es ésta la justificación de que hable de la motivación “estético/pedagógica”.
Como la lectora y el lector ya han advertido, hay una característica especialmente destacable en estos variados casos: podríamos haber adoptado, en vez de la opción polimodal, la opción “unimodal” (privilegiando el estilo B 1).8 La motivación estético/pedagógica resulta perfectamente compatible con este escenario que permite la elección de una u otra alternativa comunicacional. Una pregunta interesante es la de si siempre enfrentamos estos escenarios “permisivos” (en el contexto de los Elementos) y, después, si las motivaciones conjeturadas como subyacentes en la opción polimodal pueden ser, en todos los casos, la estética o la didáctica. Responder esta cuestión es el objeto del próximo apartado.
4
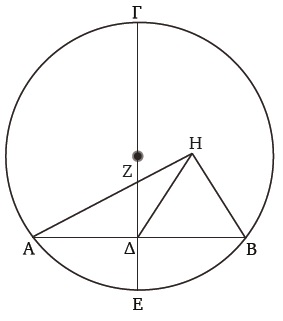
En su excelente obra The Shaping of Deduction in Greek Mathematics, Reviel Netz discute la demostración de III.1.9 He aquí la proposición:
Hallar el centro de un círculo dado.
La figura correspondiente es:
La demostración se desarrolla así: Sea el círculo dado ABΓ. Se debe “hallar el centro del círculo ABΓ”. Se traza una recta AB y se la divide en dos por el punto Δ, y a partir de Δ se traza ΔΓ, perpendicular a AB. Se prolonga ΔΓ hasta E y se divide ΓE en dos partes iguales por Z. Ahora hay que probar que Z es el centro del círculo ABΓ.
La demostración es por absurdo. Supongamos que Z no es el centro; supongamos entonces que lo sea H y trácese HA, HΔ, HB. Ahora bien, como AΔ es igual a ΔB, y ΔH es común a los triángulos AHΔ y ΔHB, los lados AΔ y ΔH son iguales respectivamente a los lados HΔ y ΔB, y la base AH (del primer triángulo) es igual a la base HB (del segundo triángulo), pues son radios del mismo círculo; por I.8, el ángulo AΔH es igual al ángulo HΔB. Pero cuando trazamos una recta sobre otra haciendo iguales entre sí los dos ángulos adyacentes, por la Def. 10 del Libro I cada uno de ellos es recto. De este modo, el ángulo HΔB es recto. Pero sabemos que el ángulo ZΔB es recto. Tenemos entonces que “el ángulo ZΔB es igual al ángulo HΔB, el mayor al menor; lo cual es imposible”. Por lo tanto, H no puede ser el centro del círculo ABΓ. “De la misma manera demostraríamos que ningún otro (lo es) excepto Z.” Concluye Euclides: “Por consiguiente, el punto Z es el centro del (círculo) ABΓ”.
¿Es esta demostración un ejemplo del fenómeno general que nos ocupa? Veamos. Por hipótesis, tenemos el círculo ABΓ. Una vez construido Z mediante los pasos referidos, lo que debemos probar es que Z es el centro. La demostración es por absurdo. Hay que probar que, para cualquier H distinto de Z, si se lo toma como centro, caemos en un absurdo. La demostración (tal como la interpreta Netz) se compondría, si usamos mi terminología, de un tramo tipo B 1, es decir, de una descripción detallada de la inferencia del absurdo a partir del supuesto de que H es el centro (H distinto de Z) y de un tramo tipo B 2, es decir, de una indicación sucinta (“De la misma manera demostraríamos que ningún otro (lo es) excepto Z”) de los infinitos casos correspondientes a puntos distintos de Z en que se demostraría el absurdo, siguiendo el patrón expuesto por B 1. Por lo tanto, podría decirse que la demostración muestra la variación secuenciada de formatos expositivos (B 1-B 2) y, a través de esta estrategia comunicacional, logra la compleción de los correspondientes requerimientos estructurales.
La parte menos detallada, la parte “meta” (B 2) es extremadamente escueta y, por ello, podríamos pensar que se aproxima a los ejemplos tipo I.17: identifica el procedimiento a seguir simplemente remitiendo al expuesto antes sin ofrecer otras pistas al lector. más allá de esta similitud superficial, existe un contraste profundo. Un indicio inequívoco de tal diferencia lo ofrece la apelación a la cuantificación: mediante la estrategia descrita en B 2 “demostraríamos que ningún otro” punto es el centro del círculo en cuestión. Luego, resulta muy natural entender que la compleción estructural de la prueba se produce apelando a una peculiar iteración infinita (indicada en B 2 ) del procedimiento ilustrado en B 1 . Con su habitual agudeza, Netz subraya la singularidad “lógica” de esta prueba: “Éste es un movimiento lógico muy interesante, dado que Euclides prácticamente promete dar un número infinito de pruebas.” (Netz 1999, p. 245; las cursivas y la traducción son mías.)
Ya se habrá notado que esta afirmación deja traslucir una diferencia relevante entre el punto de vista de Netz y la interpretación general esbozada en estas páginas. Este autor acentúa el carácter futuro de la operación demostrativa; se “promete dar” un “número infinito de prubas”. Tal aseveración parece respetar literalmente el texto.10 Mi punto de vista atribuye a este giro en la comunicación de la prueba un carácter figurado, más bien retórico: nada se deja pendiente, ni para ser “dado” o “aplicado”. Se trata nada más que de un recurso expresivo para hacer referencia a un rasgo perfectamente claro de la estructura de la demostración. Dicho de otra forma: no hay ausencia de compleción (en el nivel estructural) ni ausencia de comunicación (en el nivel expresivo).11 Se aplica una alternativa mediática orientada a la descripción de una determinada estructura demostrativa que incluye una iteración infinita de pruebas.
Netz nos enseña además algo muy importante: esta prueba no es un caso único, extraño, extraordinario en el universo euclidiano; si nos concentramos en los primeros cuatro libros de los Elementos podemos encontrar argumentos análogos en I.14, I.39, I.40, III.18 y III.19.12 Así pues, una cuestión relevante (desde mi punto de vista) es examinar con más detalle la trama de estas demostraciones, y en particular las exigencias que suponen (desde el punto descriptivo) para B 2. Retornemos pues con ese espíritu a la prueba de III.1.
El pasaje que me interesa explorar es específicamente la demostración stricto sensu (es decir: la apódeixis). Podríamos describirla de manera estilizada así:
se supone que Z no es el centro del círculo ABΓ;
se supone que H (distinto de Z) es tal centro;
se llega a la conclusión que el ángulo ZΔB es igual al ángulo HΔB, el mayor al menor, i.e., se alcanza algo que es absurdo;
luego H no es el centro del círculo ABΓ.
Se itera la demostración caracterizada por 2-4 (con las variaciones oportunas) con el fin de probar que, para cada punto distinto de Z, si se lo supone como centro del círculo, nos conduce a un absurdo;
luego, ningún punto distinto de Z es el centro del círculo ABΓ.
Por lo tanto, Z es el centro del círculo ABΓ.
Netz defiende la vigencia normativa del expediente inferencial:
Pero mientras que nosotros podemos estar impresionados por el nuevo fundamento lógico que está siendo cubierto por este movimiento, debería advertirse que nada en la práctica de Euclides apunta a que él esté muy preocupado con esta forma de argumentación. Su calma es explicable. Hay un número infinito de puntos en la misma sección del círculo en el que está Η, pero no hay problema en imaginar la prueba para todos esos casos: es decir, debe ser la misma prueba -la misma secuencia de palabras- no importa qué punto tome usted. (Netz 1999, p. 245)
Y agrega que se puede obtener el resultado (para las tres secciones restantes del círculo) con variaciones menores del procedimiento expuesto y que los otros casos son obvios: Η fuera del círculo, en su circunferencia, en la línea dada o en el diámetro.
Si revisamos los ejemplos anteriores, surge en forma nítida un patrón inferencial compartido. Así, por ejemplo, si examinamos la demostración (más en específico: la apódeixis) de I.14, encontramos ejemplificado ese patrón. Veamos. El teorema I.14 establece que:
Si dos rectas forman con una recta cualquiera y en un punto de ella ángulos adyacentes iguales a dos rectos y no están en el mismo lado (de ella), ambas rectas estarán en línea recta.
La figura correspondiente es:
La demostración es la siguiente. Supongamos que BΔ no está en línea recta con BΓ. Entonces hay una recta, digamos, BE que sí lo está, es decir: BE está en línea recta con BΓ. Por hipótesis, ABΓ y ABΔ son iguales a dos rectos. Pero como AB ha sido trazada sobre ΓBE, ABΓ y ABE son también iguales a dos rectos (por I.13). Dicho de manera breve, quitemos ABΓ de ambos y tenemos que ABE es igual a ABΔ, “el menor al mayor”, lo cual es absurdo. En consecuencia, BE no está en línea recta con BΓ. Luego leemos en Euclides:
Y de modo semejante demostraríamos esto de cualquiera otra recta que no sea la recta BΔ.
La iteración infinita de este proceso (con las variantes pertinentes) muestra que suponer que cualquier recta distinta de BΔ está en línea recta con BΓ lleva a un absurdo. Así, la hipótesis de que BΔ no está en línea recta con BΓ lleva a un absurdo. Por lo tanto, BΔ está en línea recta con BΓ. Luego, como es habitual, sigue la conclusión (sympérasma):
Por consiguiente, si dos rectas forman con una recta cualquiera y en un punto de ella ángulos adyacentes iguales a dos rectos y no están en el mismo lado (de ella), ambas rectas estarán en línea recta.
Concentremos nuestra atención nuevamente en la demostración stricto sensu:
Se supone que BΔ no está en línea recta con BΓ.
Se supone que BE está en línea recta con BΓ;
se llega a la conclusión de que ABE es igual a ABΔ, el menor al mayor, i.e., se llega a un absurdo;
luego, BE no está en línea recta con BΓ.
Se itera la demostración caracterizada por 2-4 (y las variaciones oportunas) con el fin de probar que, para cada punto distinto de Δ, si se supone que la recta correspondiente está en línea recta con BΓ, se llega a un absurdo;
luego, ninguna recta distinta de BΔ está en línea recta con BΓ.
Por lo tanto, BΔ está en línea recta con BΓ.
Este patrón común lo comparten todos los casos identificados antes.
En suma, resulta razonable entender ese patrón como esquema de una argumentación general de reductio ad absurdum y una iteración infinita de demostraciones por el absurdo “anidada” en la estructura general; esta iteración es imprescindible para el éxito de la reductio: sin aquella, ésta se desploma. Tales demostraciones son además esencialmente heterogéneas: se acentúa ese rasgo si resaltamos que (en cada una de ellas) la obtención del absurdo supone un uso decisivo (aunque implícito) de NC5 para habilitar el pasaje desde la relación parte-todo correspondiente a la relación de desigualdad respectiva.13
Pueden existir, naturalmente, muchas formas de describir el patrón mencionado, pero basta una caracterización estilizada y austera como la que se acaba de sugerir para fijar la idea principal: sin la comunicación de la iteración infinita, no hay demostración.14 Cada iteración tiene (aproximadamente) la “forma” delineada en 2-4; 5 expresa la condición de repetibilidad infinita del proceso (con eventuales variantes menores o complementos). El próximo apartado procura razonar con cierto detalle las consecuencias de esta situación para la comprensión de la expresión polimodal.
5
Antes de abordar las consecuencias de aceptar la vigencia del patrón inferencial como algo capaz de caracterizar la clase especial de demostraciones referidas en el apartado anterior, es necesario reconocer un problema serio: la interpretación de Netz dista de ser obvia. En palabras de Heath:
Simson observó que la demostración de III.1 no puede sino ser por reductio ad absurdum. Al comienzo del libro III, no tenemos nada más para basar la prueba que sobre la definición de círculo, y, a los efectos de usarla, no nos queda sino suponer que algún punto es el centro. Sin embargo, no podemos suponer que el punto que encuentra la construcción es el centro, porque eso es lo que hay que aprobar. Por lo tanto, no nos queda nada más que suponer que algún otro punto es el centro y luego demostrar que, sea cual sea el otro punto que se tome, resulta un absurdo; de donde podemos inferir que el punto encontrado es el centro. (Euclides 1908b, p. 8)
Este pasaje capta con absoluta claridad una idea fundamental: la función del resultado obtenido. Dicho de forma explícita: la contribución o aporte de esta estrategia argumental en esta prueba (y en las diversas pruebas estudiadas) asegura la unicidad del objeto geométrico en cuestión. El aspecto que no resulta plenamente iluminado es el detalle del procedimiento que permite obtener ese resultado. Así pues, ¿cuál es?
En la cita precedente no parece haber referencia alguna a un proceso de iteración (actual o potencial) de procedimientos demostrativos (aunque tampoco se excluye en forma inequívoca); el comentario de Heath sobre esta demostración encaja perfectamente con una prueba por casos (quizá suponga ocho casos, quizá menos); luego, aunque estaríamos ante un entramado argumentativo algo más barroco, esencialmente la articulación entre B1 y B2 resultaría ser la misma que en las pruebas discutidas en el apartado 1, a saber, que es siempre posible explicitar la estructura descrita por B2 a través del recurso al estilo expresivo de B1.
Sin pretender tomar una decisión de manera definitiva sobre este dilema interpretativo, esbozaré dos razonamientos que apoyan la perspectiva de Netz. En primer lugar, se evidencia una convergencia sólida (en las pruebas de la clase en cuestión) en una formulación cuantificacional peculiar, esto es, en una suerte de normalización o uniformización de la apelación a la generalidad.15 Luego, desde el punto de vista expresivo, la agrupación en una clase de tales pruebas parece plenamente justificada. En segundo lugar, no parece condecir con el estilo euclidiano que el espacio lógico (¡y justo cuando resulta tan esquivo!) se omita sistemáticamente, incluida la distinción entre las pruebas que habría que ofrecer y las que nos podemos ahorrar por su naturaleza obvia. Podría incluso concederse que Euclides no se preocupara por estas últimas, es decir, aquellas que entendiese triviales, pero sí resultaría muy llamativo que no refiriese a las omitidas y semejantes a la ofrecida previamente -si se tratara, à la Heath, de una prueba por casos-, tal como lo hace en forma habitual. La reconstrucción de Netz ofrece una alternativa que explica, por una parte, la coincidencia expresiva o estilística y, por otra, no desmiente una práctica de explicitación razonable (en términos del propósito del agente, de la comprensión del receptor y, especialmente, ¡de la presión estructural!) del espacio lógico.
La lectora y el lector sensibles a la lógica podrían manifestar aún otra perplejidad (o, quizá, una objeción): ¿es posible incorporar a la misma categoría la demostración asociada a la solución de un problema (III.1) y la demostración de un teorema (I.14)? La respuesta es afirmativa. más aún: las razones que la fundamentan revelan aspectos de gran interés. Antes de entrar en la cuestión, tal vez convenga advertir que, de estos casos sui generis bajo consideración, sólo uno es un problema (III.1) y todos los otros son teoremas (I.14, I.39, I.40, III.18, III.19). Como seguramente se recordará, la distinción entre los teoremas y los problemas se ha propuesto con el objetivo de clasificar las proposiciones que demuestra Euclides. La referencia ineludible aquí es Proclo 1970 (pp. 77-81). No discutiré la cuestión en detalle, pero, dicho en forma tosca, los problemas se proponen construir un objeto geométrico y los teoremas establecen propiedades o relaciones entre objetos geométricos ya dados. Ahora bien, Proclo señala en forma muy pertinente para nuestro asunto que “la demostración también ocurre en los problemas” (Proclo 1970, p. 81) y agrega:
[U]nas veces la demostración se usa en aras de la construcción, es decir, la empleamos para probar que lo propuesto ha sido hecho, mientras que, en otras ocasiones, merece atención por sí misma porque es capaz de exponer la naturaleza del objeto investigado. (Proclo 1970, p. 81; las cursivas son mías.)
El autor se refiere aquí al papel de la demostración en sentido estricto o apódeixis en los contextos de, respectivamente, un problema y un teorema. Como en el análisis de la polimodalidad nos concentramos exclusivamente en la demostración stricto sensu, el propósito de si se la usa “en aras de la construcción” o para “exponer la naturaleza del objeto investigado” no resulta decisivo. Estas consideraciones resultan valiosas porque acentúan un rasgo distintivo del concepto de polimodalidad: aunque, como se adelantó en las primeras páginas, se predica de la demostración como totalidad, presupone una selección de la unidad de análisis mucho más estricta: se concentra en “bloques” o “tramos” de la expresión demostrativa. Es, dicho en un sentido metafórico, una propiedad que se elucida escudriñando en “partes” o “porciones” del desarrollo expresivo de la prueba. En el caso particular de la prueba euclidiana (aprovechando la tradicional división, debida a Proclo, en diversos “momentos” o “etapas”) tal propiedad (como se señaló en su momento) retrata la dinámica expresiva especial (al abarcar, esencialmente, dos bloques) que sucede en uno de esos momentos o etapas, a saber, la apódeixis o demostración -en sentido estricto-.16 Es esta concentración o encapsulamiento de la polimodalidad la que hace posible el agrupamiento en una clase de las pruebas referidas, al margen de si la apódeixis en cuestión se encuentra en la justificación de un teorema o de un problema.
6
Ahora bien, una vez que aceptamos justificadamente la interpretación desarrollada en 4 y la posibilidad de reunir en una sola categoría tales demostraciones (más allá del tipo de proposición que justifican), la consecuencia inmediata de la identificación de aquel patrón argumental es decisiva para nuestro problema: en las pruebas euclidianas que integran esa clase se constata la irreductibilidad de B2 a B1. Dicho de otra forma, no parece posible que podamos sostener (con los recursos euclidianos) que, en las pruebas de este tipo, exista la alternativa de “parafrasear” o “traducir” B 2 a B 1. más específicamente, no puede haber una “contrapartida” que se exprese en el estilo B 1 y que capte el proceso descrito en B 2. La razón es obvia: ese proceso es infinito. Aunque cada tramo (considerado en forma individual) del tipo 2-4 se exprese en el estilo B 1, la totalidad de esos tramos (como lo exige la estructura de la demostración) no puede incorporarse. La aplicación de la condición 5 no se deja captar por el estilo B 1. Desde luego, este rasgo contrasta con las demostraciones del tipo que examiné en los apartados 1 y 2. Es fácil imaginar cómo, por ejemplo, mediante la Figura 3 y con el desarrollo textual correspondiente obtendríamos una prueba de I.16 que “tradujese” B 2 al estilo de B 1. Este “escenario permisivo” o de “indeterminación relativa” de la expresión por la estructura no es el que quedó delineado en cada uno de los ejemplos de la clase que se introdujo en el apartado 4.
Tomemos, por ejemplo, III.1. Deberíamos en este caso poder exponer todas y cada una de las instancias (infinitas) de la secuencia 2-4 correspondiente, digamos para un punto h', h'',… Esto, obviamente, es imposible. Podríamos quizá resumir la situación así: las demostraciones con estructura finita permiten la “paráfrasis” en el sentido indicado, pero no la admiten demostraciones con una estructura infinita (i.e., cuya explicitación supondría una serie infinita de pasos).17
Esta relación novedosa entre B 1 y B 2 revela una articulación original entre la expresión y la estructura. En los casos de los apartados 1 y 2 la expresión de la demostración podía escogerse libremente, y en tal sentido el agente podía optar por una formulación polimodal o unimodal. Para retomar el ejemplo de I.16, en ese caso podemos optar por una comunicación polimodal o por una unimodal (estilo B 1), pero no poseemos la misma libertad expresiva o estilística en el caso de III.1. En los casos como III.1, la expresión es determinada por la estructura.
Aunque la estructura influye siempre en la expresión, merece destacarse que estamos aquí ante un contraste entre dos grados netamente diferenciables de incidencia. Dado este panorama, parece oportuno revisar nuestras conjeturas respecto a las posibles motivaciones subyacentes en la elección de los formatos expresivos. La conjetura estética/ pedagógica parece dar cuenta de demostraciones polimodales como las que discutimos en los apartados 1 y 2, pero no parece adecuado proponerla (al menos como dominante o principal) en el caso de los ejemplos del apartado 4 debido a la diferencia que acabo de recalcar.
Deberíamos entonces sumar a la motivación estético/pedagógica aquella que de manera clara anima la aplicación de tales pruebas; parece razonable, dado su origen estructural, denominarla “lógica” (en un sentido lato).
El siguiente cuadro ilustra las consideraciones previas acerca del contraste entre las dos variantes o estilos polimodales (A y B, correspondientes a los ejemplos de, respectivamente, los apartados 1-2 y 4):
| Estilo A | Estilo B | |
| expresión polimodal | Sí | Sí |
| traducción posible B2-B1 | Sí | no |
| determinación por la estructura del formato de la expresión |
no | Sí |
| motivación | estética/pedagógica | lógica |
Conviene ahora sintetizar y contextualizar algunas observaciones previas. La introducción de un nivel meta-demostrativo (a través del recurso a la exposición polimodal) supone efectos comunes y específicos según nos encontremos ante los casos A o B. En cualquiera de las dos alternativas supone una revisión o relectura de B 1 a partir de B 2. Quizá podríamos decir que, primero, decodificamos B 1 como prueba sin más y, después, por efecto de B 2, como type, modelo o paradigma demostrativo. Un efecto particular, cuando tomamos la alternativa B, es el surgimiento novedoso de una diferenciación en términos de poderío expresivo: B 2 “dice más” (en cierto sentido) que B 1. Es obvio que no se trata exclusivamente del estatus meta-demostrativo de B 2, sino del tipo particular de operación que procura describir. Dicho de otra forma: si entendemos B 1 desde el nivel del lenguaje objeto, la naturaleza meta de B 2 es condición necesaria, pero no suficiente, de la superioridad expresiva y, en consecuencia, de su irreductibilidad.
Quizá sea igualmente importante resaltar que (en otro sentido) B 1 “dice más” que B 2. Como ya se destacó, B 1 ofrece información más detallada, más fina del proceso inferencial; B 1 es absolutamente independiente (desde el punto de vista expresivo) de B 2, pero lo inverso no vale: B 2 se apoya en forma sustantiva en B 1. Esta relación (característica del estilo polimodal) puede entenderse de manera plena en términos relativos y no existe ninguna necesidad (desde el punto de vista del análisis desarrollado) de descontextualizarla.
Por último, Netz no acentúa en detalle estos diversos aspectos, pero sin duda los concebiría como parte del apoyo indirecto que ofrece la expresión polimodal en su respuesta al desafío de la peculiar generalidad de la demostración euclídea.18
7
Varios autores han subrayado, de forma más o menos directa, la vigencia de la distinción entre la estructura y la expresión (o variantes de este contraste). Así, por ejemplo, Oswaldo Chateaubriand escribe:
O se dice que las secuencias lingüísticas utilizadas en la comunicación de las demostraciones son las demostraciones, o se dice que describen demostraciones, o indican demostraciones, o comunican demostraciones. (Chateaubriand 2005, p. 284)
Por su parte, Marcus Giaquinto expresa lo siguiente:
Debemos distinguir entre una demostración y una presentación de una demostración. (Giaquinto 2008, p. 24; las cursivas son mías.)
Ambos autores proponen una distinción entre la demostración y su expresión, comunicación, descripción o presentación -aunque no deseo sostener que estos filósofos compartan el enfoque acerca del contraste aludido y, en particular, el modo de entender lo que denominé “estructura”-. Sin duda, es éste precisamente el componente más crítico del binomio.
Ahora bien, he recurrido aquí a un uso metodológicamente robusto y ontológicamente austero de la estructura demostrativa. Esta opción ha desempeñado un papel esencial en la caracterización y análisis de la expresión polimodal, y ha sugerido además una suerte de tríada de campos gravitacionales que es preciso atender a la hora de elucidar (en términos filosóficos) la expresión de la demostración matemática: agente, destinatario, estructura. Para ello no fue necesario otorgarle ningún estatus especial al plano estructural ni se lo ha sustraído en forma absoluta de las dinámicas de la comunicación matemática. Aquello que cuenta como estructura de una demostración reúne las presiones lógicas (en sentido lato) y se expresa o representa en formas variadas. No se establecieron para la estructura ni niveles máximos ni niveles mínimos generales de especificación inferencial; luego, no hay necesidad de adoptar ningún lenguaje ideal, último, final, más allá de cuyas capacidades elucidatorias o analíticas (desde un punto de vista lógico) no se pueda progresar.
Chateaubriand ofrece una sugerencia interesante que tal vez nos permita, al reformular el contraste entre las modalidades expresivas que denominé aquí B 1 y B 2, entender mejor la flexibilidad de mi concepción. Este filósofo habla de “comunicación literal de una demostración” y “descripción de una demostración”.19 Quizá podríamos decir que la tarea que realiza B 1 es o se aproxima a la comunicación literal y la labor de B 2 es una descripción de la demostración. Por las observaciones anteriores, estas denominaciones no debieran adoptarse en un sentido absoluto. Desde mi perspectiva, no hay algo así como la comunicación literal de una prueba sin más; toda comunicación literal lo es respecto de un contexto determinado. Y lo mismo cabría decir de la descripción. En este sentido relativizado, las denominaciones propuestas por Chateaubriand resultan satisfactorias. Esta contextualización y esta negación de un lenguaje “último” no suponen, desde luego, compromisos con ninguna clase de inefabilidad. Tampoco se supone ningún compromiso ontológico oneroso respecto a la estructura. En síntesis, estas modestas exploraciones sobre la demostración euclidiana permiten ilustrar un uso filosófico razonable de la distinción metodológica entre la expresión y la estructura.











 nova página do texto(beta)
nova página do texto(beta)