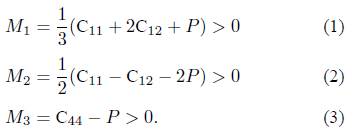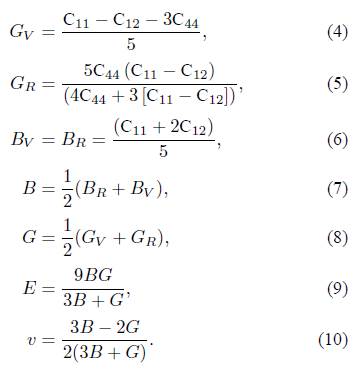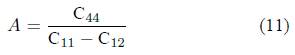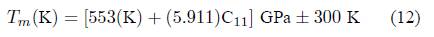1. Introduction
In recent years, Laves phase materials have been found to have unique properties, making them attractive for structural applications with high temperatures [1] and also to their usefulness in technical applications. Intermetallic compounds, which have been attractive for their Curie temperatures and the simple cubic laves-phase (C15) crystal structure, have also gained a great deal of attention from researchers due to the fascinating features of polymorphism, unusual magnetic properties, electrical properties and possible applications such as superconducting, giant magnetostrictive materials and hydrogen storage materials [2]. Cubic Laves phase intermetallic compounds REX2 (where RE-= rare earth elements and X= transition metal) attracted a lot of attention due to peculiar meta-magnetic transitions that derive from the coexistence and interaction of magnetic moments of strongly localized RE 4f electrons and itinerant 3d electrons of the X [3]. Binary Laves phases with AB2 composition are part of the topologically close-packed (TCP) structures. These systems crystallize into three structures: face centered cubic C15 (MgCu2), hexagonal C14 (MgZn2), and double-hexagonal C36 (MgNi2) [4]. Because of their FCC-based structure, the C15 Laves phases are predicted to exhibit better deformability than the other two Laves phases among the three Laves phase structures [5]. Few studies have been theoretically and experimentally investigated on LaCo2 compound. Robertson et al. [6] stated that the LaCo2 has the cubic MgCu2-type structure with a lattice parameter of 7.449 A. Another experimental study by Nakamura et al. [7] reported on synthesizing the cubic LaCo2 by 59Co NMR experiments; they concluded the presence weak ferromagnetism in LaCo2. In another work, Sasaki and coworkers [8], studied the magnetic properties of LaCo2 in a MgCu2 structure by first-principles electronic structure calculations by utilizing the Korringa-KohnRostoker (KKR) method for the electronic structure calculation.
To the best of our knowledge, there is no theoretical work available in the literature on the detailed physical properties of the Lave phase LaCo2 compound, which is the central focus of our paper. In this study, we have investigated the structural, elastic and electronic properties of the LaCo2 intermetallic compounds in cubic C15 (MgCu2 ) phase using first principle calculations, which are followed by the transport properties using semi-classical Boltzmann theory in order to deeply understand the ground-state properties and provide accurate theoretical results.
2. Method of calculations
The computation has been performed by using full potential linearized augmented plane wave (FP-LAPW) method within the spin polarized density functional theory (DFT) [9,10] implemented in Wien2k code [11,12]. We have used the generalized gradient approximation GGA with Hubbard (U) as exchange correlation functional [13,14]. The cut-off parameter value used is RMT*K max = 8, (where RMT is the smallest radius in the muffin spheres and K max represents the cutoff in the plane wave). The radii of the muffin-tin sphere RMT were 2.5 Bohr for La and 2.41 Bohr for cobalt. The cut-off energy, which defines the separation among the core and the valence states, was set at −7.0 Ry. The maximum value for partial waves inside the atomic sphere is lmax = 10 while the G max parameter was taken to be 12.0. For the Brillouin zone (BZ) integration a tetrahedron method with 8×8×8 special k-points in the irreducible wedge of BZ was used [15]. To achieve a correct convergence of all the calculations for our compounds; the Hubbard parameter was employed for the strongly correlated elements. We applied U on the 3d orbital of Co atoms. Hence, we used the values of Coulomb interaction parameter U = 4 eV and the Exchange parameter J = 0.9 eV [16]. The calculations of the transport properties of LaCo2 in C15-Laves phase were performed based on the calculated spin-polarized electronic band structures using the semi-classical Boltzmann theory [17] as implemented in the BoltzTraP code with a dense mesh of 100000 k-points.
3. Results and discussions
3.1 Structural properties and formation energy
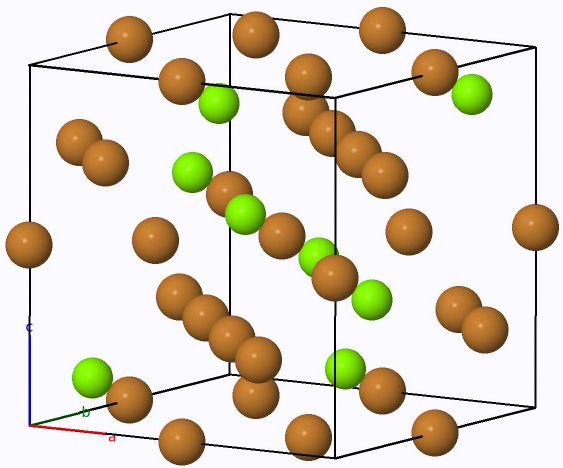
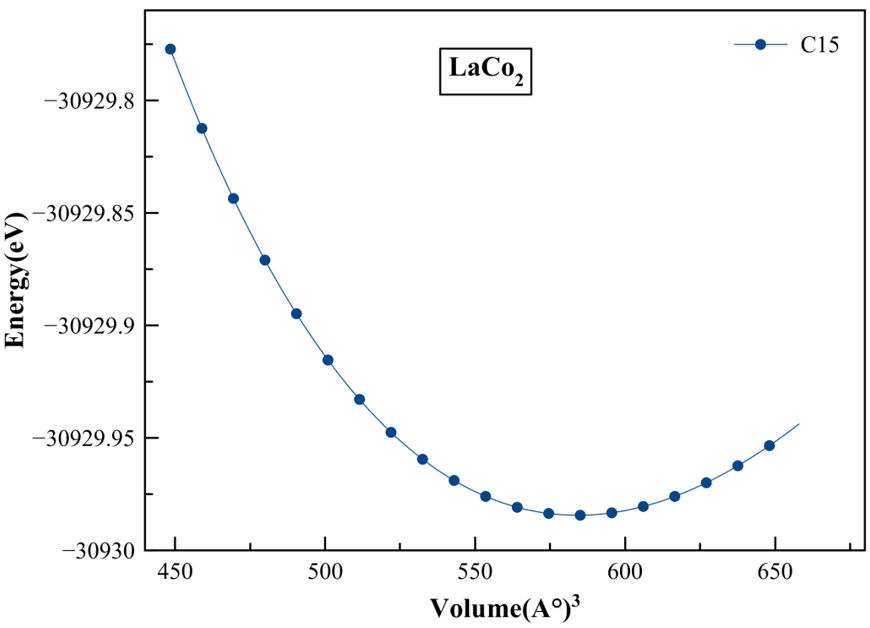
The Laves phase LaCo2 compound investigated in the present work crystallizes in the face centered cubic MgCu2 type structure with space group Fd-3m (No. 227). The La atoms occupy the tetrahedral 8a Wyckoff site(1/8,1/8,1/8) and the Co atoms occupy the octahedral 16d site(1/2,1/2,1/2) [18], as shown in Fig. 1. We used the experimental lattice constant to start the calculations. The optimized lattice parameters a, cell volume V , bulk modulus B, and the first pressure derivative of the bulk modulus B’ recorded in Table I, are determined by fitting the total energy per cell with the Birch-Murnaghan equation of state [19,20]. The Energyoptimization curve of LaCo2 using GGA approximation is also shown in Fig. 2. The calculated lattice constant of LaCo2 intermetallic is 7.274 Å so we can deduce that the experimental and theoretical values are in good agreement.
TABLE I The calculated equilibrium Lattice constant a (Ao), equilibrium volume V (Å3), bulk modulus B (GPa), first order pressure derivative B’, and the formation energy ∆E (meV) of the LaCo2 compound.
We therefore measured the formation energy for LaCo2 intermetallic compound in order to study the relative phase stability. The formation energy (∆E) can be calculated by the following expression [21]:
where
3.2 Mechanical stability and elastic properties
The mechanical stability of materials under the effect of hydrostatic pressure has a great influence on their performance in industrial and technological applications. Furthermore elastic stiffness constants of solids are very important material parameters because they provide a connection between mechanical properties and dynamic information on the nature of the forces operating in solids, in particular for the stability, stiffness, brittleness, ductility, material anisotropy and the propagation of elastic waves in the normal material mode [22].
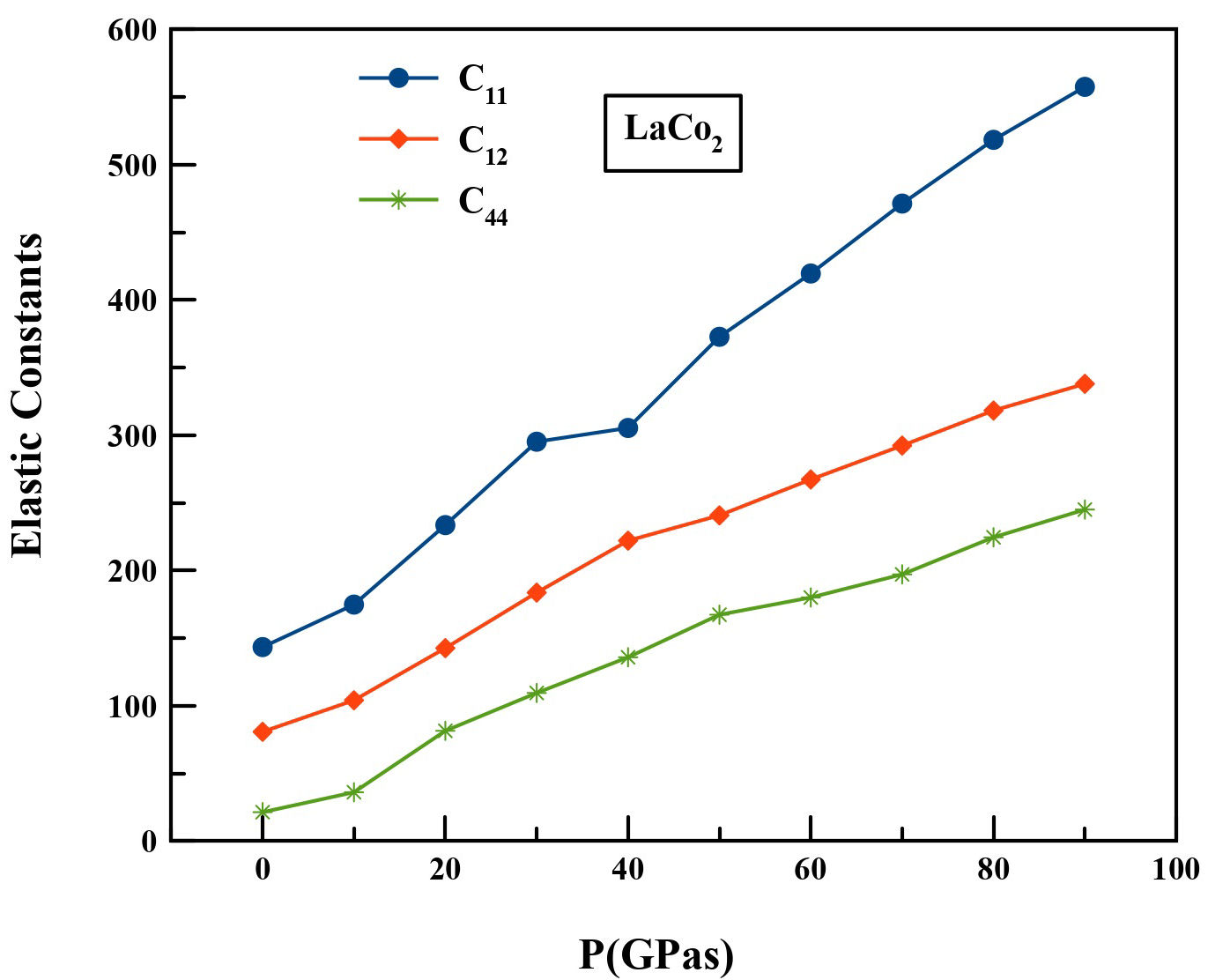
It is also essential to perform the calculations of the pressure dependence of the elastic constants for LaCo2. Since the intermetallic compound corresponds to the cubic crystal, it has three independent elastic constants C11, C12 and C44. Table II displays the determined elastic constants of LaCo2 at pressures of up to 90 GPa. We believe that this is the first work that shows the elastic constants of LaCo2 under pressure, and there are no comparable studies in the literature. So our study should encourage the experimental confirmation of these results in future.
TABLE II Calculated elastic constants Cij (GPa) of LaCo2 under hydrostatic pressure up to 90 GPa.
| P(GPa) | C11 | C12 | C44 |
| 0 | 143.41 | 80.78 | 21.38 |
| 10 | 174.827 | 104.081 | 36.11 |
| 20 | 233.585 | 142.641 | 81.516 |
| 30 | 295.221 | 183.692 | 109.496 |
| 40 | 305.385 | 222.054 | 135.88 |
| 50 | 372.770 | 240.778 | 167.335 |
| 60 | 419.55 | 267.31 | 180.076 |
| 70 | 471.256 | 292.356 | 197.155 |
| 80 | 518.356 | 318.265 | 224.561 |
| 90 | 557.53 | 337.995 | 245.07 |
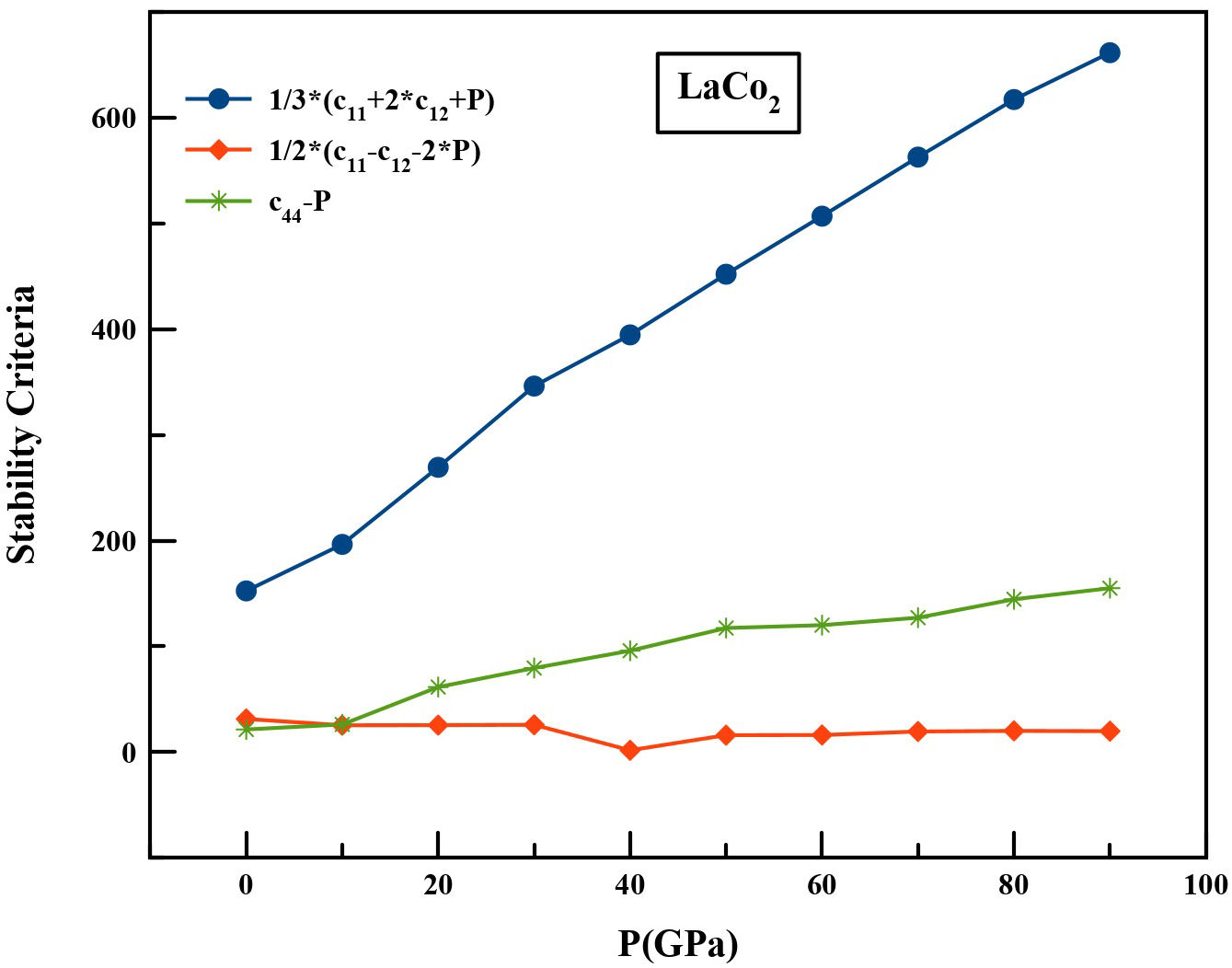
From Table II, the measured values of the elastic constants under ambient conditions properly follow the cubic stability criteria [23]: C11 > 0, C44 > 0, (C11 - C12) > 0, (C11 + 2C12) > 0, C12 < B < C11. Our LaCo2 compound in the C15 structure is therefore mechanically stable. But these stability criteria are only valid in the case of zero pressure [24]. For a cubic material under hydrostatic pressure, the generalized stability criteria are summarized as follows:
Figure 3 represents the variation of the generalized stability criteria Mi, as a function of the hydrostatic pressure in an interval of 0 to 90 GPa. According to our calculations, the Mi values obtained increase with increasing pressure, which means that the LaCo2 compound keeps its rigidity under this pressure interval.
An estimation of ductility and brittleness can be provided from the Cauchy pressure value (C12−C44), if it is negative the material is expected to be brittle and positive values as ductile. Furthermore the Cauchy pressure is used to define the angular character of atomic bonding in metals and compounds [25]; a negative value means that the material is nonmetallic with directional bonding and the material is supposed to be metallic if the Cauchy pressure is positive [26]. From Table III, it is evident that the values of the Cauchy pressures of LaCo2 at ambient condition and under all the applied pressures are positive approving the ductility and the metallic behavior of this compound.
TABLE III The calculated bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), B/G values, Poisson’s ratio v and anisotropy factor A of LaCo2 compound under hydrostatic pressure.
| P(GPa) | B | G | E | B/G | v | A | C12−C44 |
| 0 | 101.657 | 24.921 | 70.224 | 4.079 | 0.385 | 0.683 | 59.4 |
| 10 | 127.663 | 35.813 | 98.257 | 3.565 | 0.372 | 1.021 | 67.971 |
| 20 | 172.955 | 64.495 | 178.245 | 2.682 | 0.348 | 1.793 | 61.125 |
| 30 | 220.868 | 83.519 | 233.057 | 2.645 | 0.344 | 1.964 | 74.196 |
| 40 | 249.831 | 84.786 | 260.459 | 2.947 | 0.346 | 3.261 | 86.174 |
| 50 | 284.775 | 115.232 | 331.237 | 2.471 | 0.328 | 2.536 | 73.442 |
| 60 | 318.057 | 127.476 | 362.819 | 2.495 | 0.331 | 2.366 | 87.234 |
| 70 | 351.99 | 143.569 | 403.365 | 2.452 | 0.330 | 2.204 | 95.202 |
| 80 | 384.962 | 163.339 | 455.361 | 2.371 | 0.324 | 2.245 | 93.704 |
| 90 | 411.173 | 177.544 | 496.057 | 2.316 | 0.320 | 2.233 | 92.925 |
The Pugh’s ratio (B/G) [27,28] is an another stability criterion to determinate whether the material is ductile or brittle. If B/G > 1.75 the material is ductile or otherwise brittle. It is evident from Table III that LaCo2 compound is ductile at ambient pressure and that the ductility decreases gradually with increasing pressure. This agrees well with the Cauchy pressure estimation.
The polycrystalline elastic moduli can be computed using the Voigt-Reuss-Hill (VRH) method [29], based on the elastic constants. The appropriate equations are given as follows for the cubic structure:
Here, B, G and E are the polycrystalline bulk modulus, shear modulus and Young’s modulus, respectively. v is the Poisson ratio.
Figure 4 shows the pressure dependence of bulk, shear, and Young’s moduli of C15-type LaCo2. It is clearly seen that the value of B, which represents the resistance of the crystal to the volumetric change, increases with the increase of the pressure, which means that the presence of external pressure increases resistance to deformation.
Additionally, the shear moduli and Young’s modulus are the measure of resistance to reversible deformation by the applied shear force. The value of G and E increases with increasing the external pressure. this implies that, for LaCo2 the resistance to shear deformation and the stiffness are increased with the increase of pressure respectively.
Poisson’s ratio v is another rule used for determining the ductility and brittleness of a compound. The material has a ductile nature if its value is greater than 0.26; otherwise, the material is considered to be brittle. Table III shows that Poisson’s ratio for LaCo2 is greater than 0.26, which confirms its ductile nature. Poisson’s ratio v also gives knowledge about the bonding nature in a material. According to this limit the type of material bonding will be ionic if ≈ 0 : 25, covalent if ≈ 0 : 10 and metallic if ≈ 0 : 33. For our compounds the v is found close to 0.33 and hence major bonding in these materials is metallic [30].
Zener’s anisotropy factor (A) reveals the degree of the elastic anisotropy of the solid. For a perfectly isotropic material, A will take the value equal to 1; deviation from 1 shows anisotropic nature of the material [31,32]. For LaCo2 the values of A which are listed in Table III, are calculated by using the following formula at different pressures:
The determined values of A are found to be different than unity, suggesting the material will have elastic anisotropic nature.
In addition, the melting temperature, which is another thermodynamic quantity, has been determined using the following empiric expression as mentioned below [33,34].
The corresponding value observed for the present alloy is 1400.69 ± 300 K thus shows that the material has a great capacity to preserve its crystal structure over a wide range of temperatures.
3.3 Electronic properties
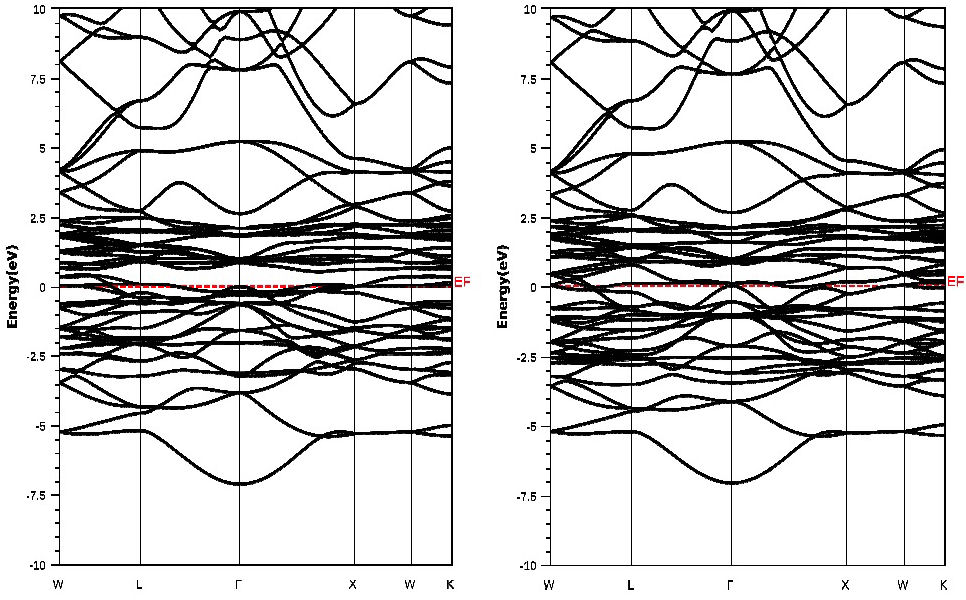
Figure 5 displays the computed spin-polarized band structures for LaCo2 at the measured equilibrium lattice constants along with the high symmetry directions in the Brillouin zone using the GGA+U method. This figure shows, in both spin configurations, an overlap between the valence and the conduction bands around the Fermi level. In addition, at the Fermi level there is no band gap, which indicates the metallic nature of our compound.
It is well known that the density of states at E F , N(E F ) tends to uncommon transport properties, since both spin-up and spin-down densities contribute to the E F states. Analogous behavior has been reported in TbFe2, TbCo2 and RENi2 (RE= Dy, Ho and E r ) compounds [35,36]. Consequently, the bands which cross E F are responsible for the transport properties of the compound and the bands which do not cross E F can make a negligent contribution to the transport properties [35].
Furthermore, the total density of states of the compound (for all atoms in a unit cell) and the partial DOS (per atom) were determined using GGA + U approximation. The curve is shown in Fig. 6. The spin-up and spin-down, along with the TDOS, are found to be anti-symmetrical, which indicates that the LaCo2 is in a ferromagnetic state. These findings can be due to the contribution of the 3d states of cobalt (Co) and the contribution of the 4f states of Lanthane (La) as well to the TDOS.
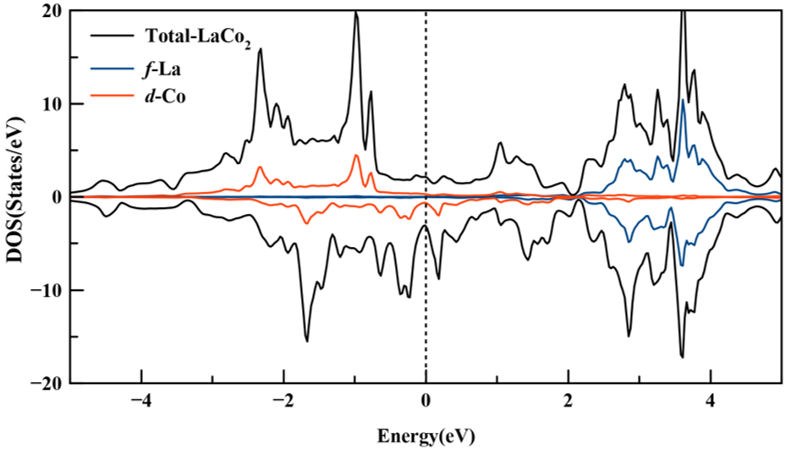
FIGURE 6 The total and partial density of states of LaCo2 (spin up and spin down) obtained with GGA + U calculations.
Moreover, the energy dispersion spectrum is observed to cross the Fermi level (E F = 0 eV), which is another indicator that this compound is potentially electrically conductor. Indeed, the low energy region, which is located around −5 and 0 eV, is mainly filled by the d states of the Co atoms. The region above (E F = 0) from 2 to 4 eV is dominated by 4f states of Lanthane (La) and the majority of the total DOS (from −5 to + 2 eV) is governed by the 3d states of Co.
3.4 Transport properties
The thermoelectric properties were performed within relaxation time approximation implemented in the BoltzTrap code, based on the Boltzmann transport theory. Effective thermoelectric materials should have high electrical conductivity (σ/τ), large Seebeck coefficient (S) and low thermal conductivity (k e /τ). We need to maintain the density and mobility of the charge carriers in order to achieve maximum electrical conductivity.
3.4.1 Electrical conductivity
To ensure that the examined compound is sufficient to provide maximum effectiveness in the E region. We have plotted the electrical conductivity of LaCo2 compound at three constant temperatures 300, 600 and 900 K as a function of chemical potential (µ − E F = ±2 eV) for both spin polarized channels as shown in Fig. 7. From the figure, we can see that for spin up channel of LaCo2 a remarkable rise in electrical conductivity occurs just above and below E F to attain the maximum value of approximately 3.73 × 1020 (Ωms)−1 around µ−E F = −0.11 eV at temperature 300 K for n-type conductions, and 3.78 × 1020 (Ωms)−1 at 300 K around µ−E F = 0.09 eV for p-type conductions. While for the spin down case a maximum value of about 4.01 × 1020 (Ωms)−1 was achieved at 300 K and µ − E F = −0.08 eV for n-type conductions and about 2.96 × 1020 (Ωms)−1 at 300 K and µ − E F = −0.09 eV for p-type conductions.
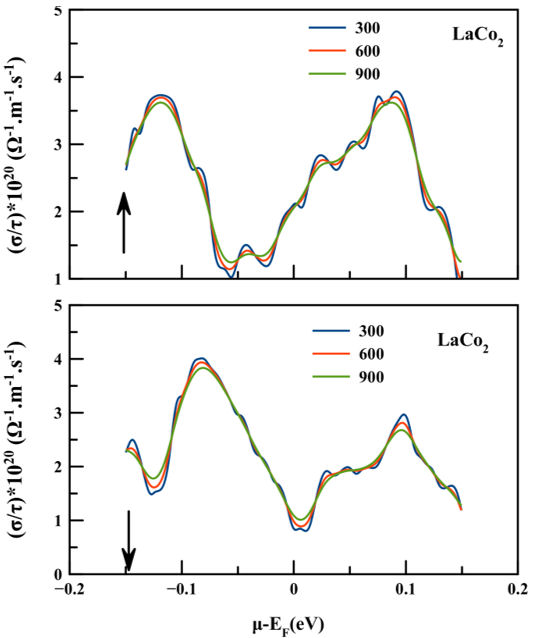
FIGURE 7 The electrical conductivity of LaCo2 for both spin configurations as a function of chemical potential at three constant temperatures (300, 600 and 900) K.
It is obvious from the above interpretation that the holes play an major role in achieving the highest values of electrical conductivity in the spin up configuration and that the electrons play a important role in the spin-down configuration.
3.4.2 Electronic thermal conductivity
The thermal conductivity is generally composed of two parts, the first one coming from the electronic contribution κ e (electron or hole) and the second one generated by lattice thermal conductivity κ l (phonon contribution). We should underline that BoltzTraP code only calculates the electronic part κ e .
The electronic thermal conductivity is measured As a function of chemical potential (µ−E F = ±0.15 eV) for both spin configurations of LaCo2 compound. Figure 8 shows that a significant increase in thermal conductivity occurs with an increase in temperature. And the temperature 900 K generated the highest κτ values, while 300 K is the adequate temperature giving the lowest κτ/e values within the chemical potential range µ−E F = +0.15 eV. So the materials studied provided optimal efficiency in this range of chemical potential.
3.4.3 Seebeck coefficient (Thermopower)
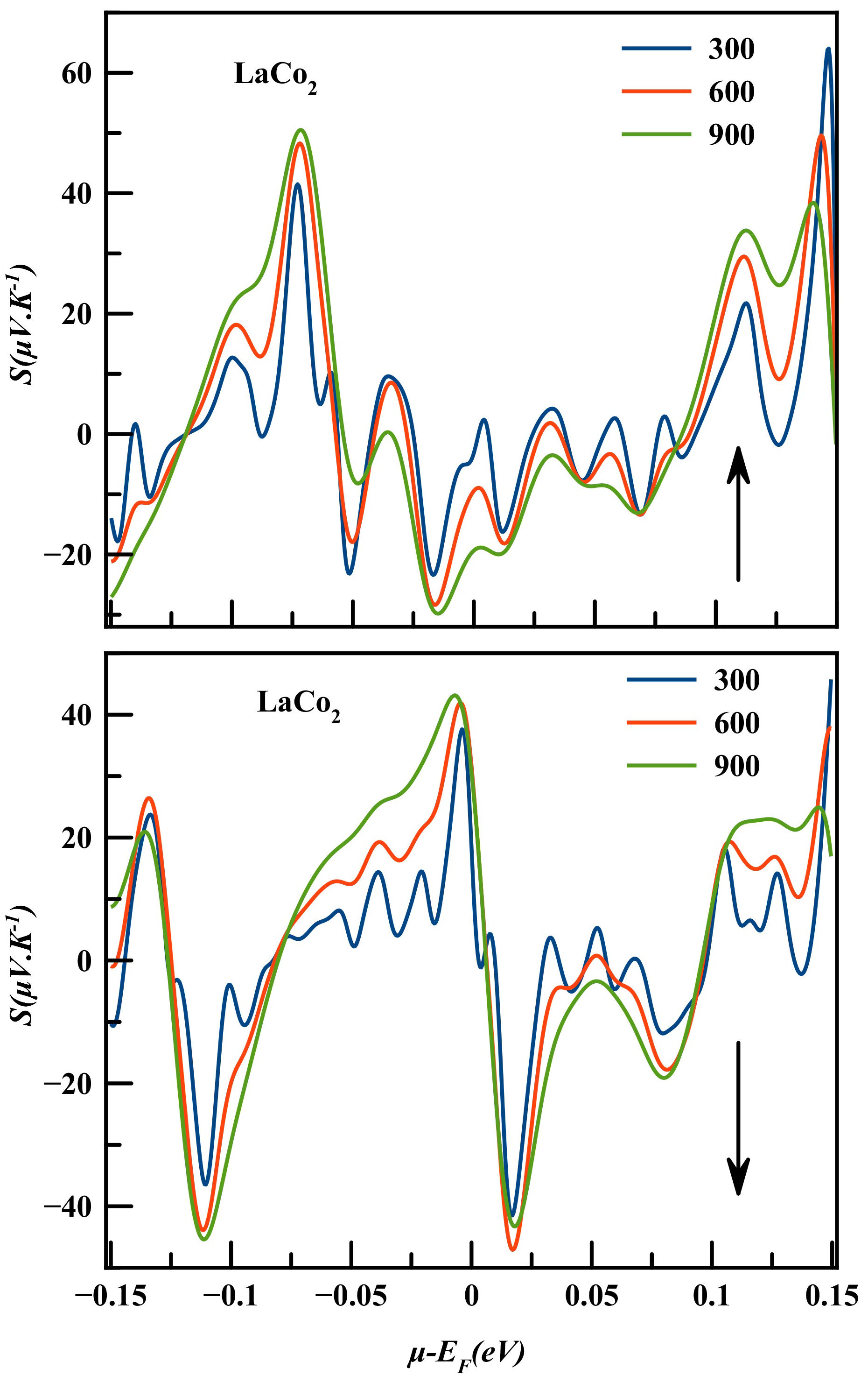
The Seebeck coefficient indicates the magnitude of an induced thermoelectric voltage regarding the temperature difference throughout the material [1]. Positive Seebeck coefficient values signify that hole-type carriers dominate the thermoelectric transport in the material, while negative values of the Seebeck coefficient signify the dominance of electron type carriers.
Figure 9 illustrates the chemical potential (µ − E F = ±0.2F eV) dependence of Seebeck coefficient of LaCo2 compound at temperature values of 300 K, 600 K and 900 K for both spin configurations. It has been found that for spin up channel of LaCo2 the highest value of Seebeck coefficient for p-type conductions of about 64.02 µV/K is achieved at 300 K for µ − E F = 0.14 eV. And for n-type conductions of about −29.83 µV/K at 900 K for µ − E F = −0.014 eV. While for spin down channels of the highest value of Seebeck coefficient for p-type conductions is about 45.74 µV/K at 300 K for µ−E F = 0.14 eV, while for n-type conductions is about −47.09 µV/K at 600 K for µ − E F = 0.017 eV.
3.4.4 Power factor (P)
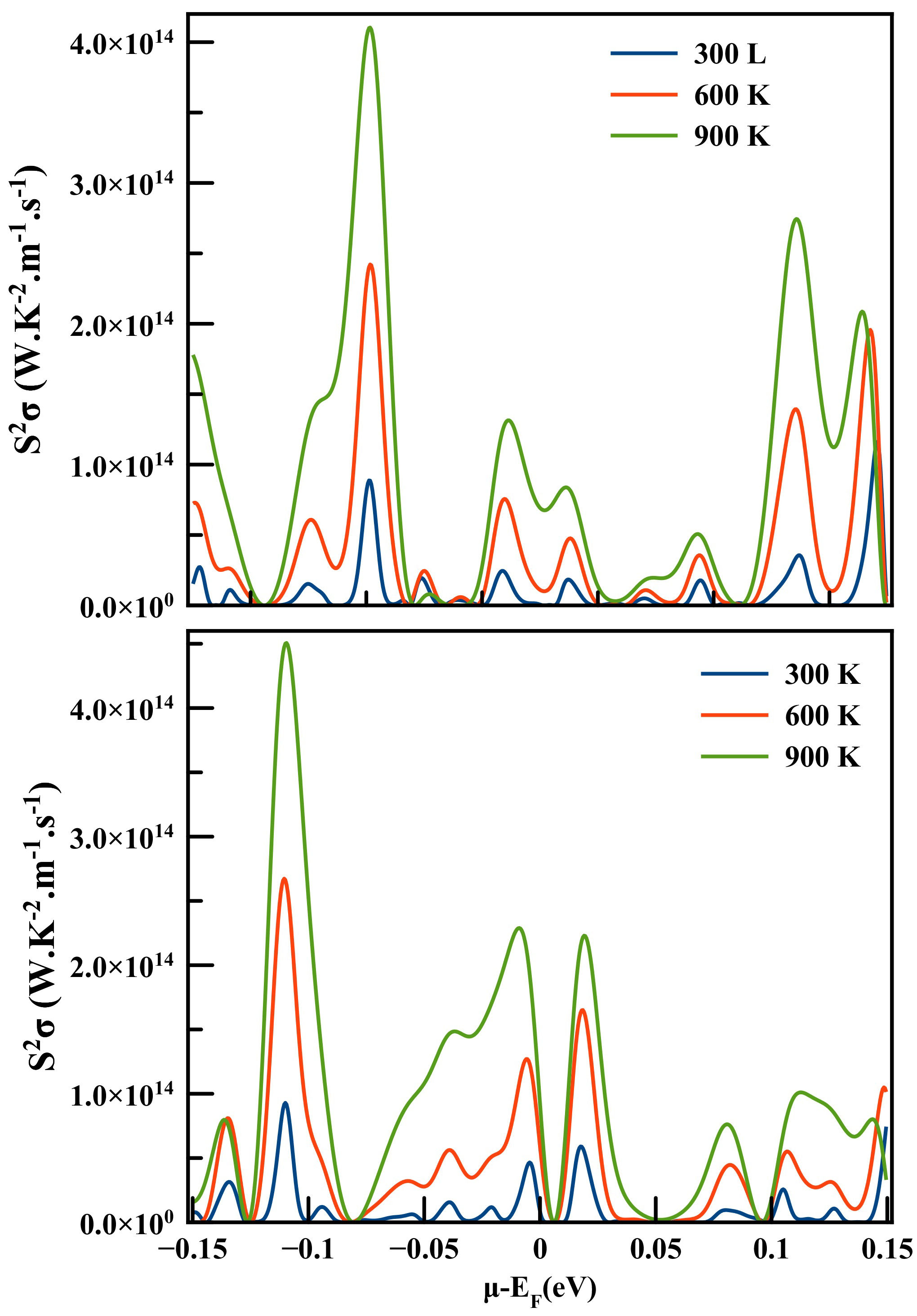
The power factor (PF=S2 σ), which is essential to explore the efficiency of the thermoelectric material, is plotted against chemical potential µ − E F = ± E 0.15 eV in Fig. 10 at three temperatures 300, 600 and 900 K for both spin configuration of LaCo2. In the spin up channel, the highest value of power factor of about 4.1 × 1014 W/mK2s is achieved at 900 K for µ − E F = −0.07 eV, 2.42 × 1014 W/mK2s is achieved at 600 K for µ − E F = −0.07 eV and 1.16 × 1014 W/mK2 s is achieved at 300 K for µ − E F = 0.14 eV. Although the spin down channel, shows the highest value of about 4.5×1014 W/mK2s at 900 K for µ−E F = −0.1 eV and 2.67×1014 W/mK2s at 600 K for µ−E F = −0.11 eV, while it is 0.92 × 1014 W/mK2s at 300 K for µ − E F = −0.11 eV.
4. Conclusion
Overall, we have investigated the structural, elastic, electronic, and thermoelectric properties of Laves phase LaCo2 using FP-LAPW method with GGA+U approximation for exchange and correlation effect and using the Boltzmann transport equation. The equilibrium lattice parameters evaluated are consistent with other data values cited in the previous studies. We have measured and discussed for the first time the elastic constants, Cauchy pressure, bulk modulus, shear modulus, Young’s modulus, of the cubic laves phase intermetallic compound LaCo2. The research suggests that according to the elastic stability of the C15 structure, LaCo2 is mechanically stable with a pressure range of 0 to 90 GPa. The investigated Cauchy pressure, Pugh’s ratio and Poisson’s ratio of this Laves phase indicate the ductile nature. From the band structure diagram, the valance and conduction bands are overlapped with each other at Fermi level, indicating that the material possesses metallic characteristics. In addition, transport coefficients including electrical conductivity, thermal conductivity, Seebeck coefficient and power factor have been determined using BoltzTraP code. The increase in the Seebeck coefficient leads directly to the rise of the power factor which is extremely high, making our compound an ideal candidate for spin-voltage generator components.











 nova página do texto(beta)
nova página do texto(beta)