1. INTRODUCCIÓN
Por lo general, la Formación de Profesores de Matemáticas (FPM) se entiende como un área de prácticas educativas y de investigación surgida a partir del reconocimiento del importante rol que desempeñan los profesores en el aprendizaje matemático de sus alumnos (Lerman, 2001; Sfard, 2004). Desde esta perspectiva, la FPM comprende todo fenómeno concerniente al aprendizaje y desarrollo profesional del profesorado de matemáticas, producido en cualquiera de las etapas del ciclo de vida de la carrera docente (inicial, principiante y continua) mediante la implementación de actividades formativas diversas y dinámicas (Krainer y Llinares, 2010).
En la etapa de formación inicial, una problemática que afecta los procesos de aprendizaje de los futuros profesores puede resumirse en la débil relación entre la preparación disciplinaria y la preparación profesional que se establece en los programas universitarios de formación docente de distintos países (Baldin y Malaspina, 2018; Ruiz, 2017), incluido Chile (Brandt, 2010; Manzi et al., 2012). La atención puesta sobre esta problemática ha llevado a los investigadores a interesarse especialmente tanto en el saber disciplinario y didáctico requerido para enseñar matemáticas, como en los modos de incorporar este saber a los programas de formación (Tatto et al., 2009). Al respecto, Liljedahl et al. (2009) han afirmado que las principales preocupaciones de la formación inicial del profesorado son comprender los procesos de adquisición del saber para la enseñanza de las matemáticas y promover tales procesos en la formación de los futuros profesores.
Dada la situación anterior, tanto el diseño como la implementación de entornos de aprendizaje (p. ej., Castellanos et al., 2018; Ivars et al., 2018; Prieto y Valls, 2010; Sáenz-Ludlow y Athanasopoulou, 2012) adquieren relevancia para los programas de formación inicial del profesorado, ya que estos dispositivos (los entornos), entre otras posibilidades, pueden provocar que los futuros profesores movilicen el saber necesario para enseñar matemáticas a partir de la resolución de situaciones problemáticas propias de la dinámica de trabajo en el aula (Carrillo y Climent, 2009; Llinares, 2020). En la mayoría de los casos, estos entornos son diseñados e implementados en atención a las necesidades, demandas y expectativas particulares de la realidad escolar que envuelve a los programas de formación inicial en cada país.
En el caso de Chile, las necesidades de la formación inicial están descritas en los Estándares Orientadores para Carreras de Pedagogía en Educación Media (EOCP), un documento oficial dirigido a las Facultades y Escuelas de Educación del país que ofrece “una orientación acerca de los conocimientos y habilidades necesarias que debería manejar el egresado de pedagogía para enseñar estas disciplinas, sobre la base del criterio de expertos” (Ministerio de Educación [MINEDUC], 2012, p. 8). Los estándares pedagógicos y disciplinarios del área de Matemática se organizan en cinco categorías o subáreas, entre ellas Geometría. Dentro de esta categoría, el estándar 12 revela la necesidad de que futuros profesores de matemáticas se preparen para:
[...] conducir el aprendizaje de los estudiantes en la realización de las construcciones geométricas con regla y compás de figuras elementales, justificando y explicando los procedimientos mediante lenguaje geométrico. Utiliza procesador geométrico para lograr la comprensión de los estudiantes en los temas de transformaciones del plano y construcciones geométricas. (MINEDUC, 2012, p. 115)
El énfasis del documento EOCP en el desarrollo del conocimiento y de las habilidades para la enseñanza de las construcciones geométricas tiene sentido si se consideran los resultados de investigaciones que evidencian las dificultades de los futuros profesores chilenos para realizar construcciones con regla y compás o con algún software de Geometría Dinámica (SGD). Por ejemplo, Rosales y Guzmán (2016) han concluido que los futuros profesores que logran realizar construcciones geométricas con SGD, muchas veces evitan describir y justificar los procedimientos empleados, desconocen el valor de la medición para verificar la consistencia geométrica de sus construcciones y restan importancia al papel del software como instrumento de construcción. Este hecho revela lo importante que resulta, en el contexto chileno, realizar investigaciones centradas en las condiciones de producción del saber para la enseñanza, relacionado con las construcciones geométricas producidas con algún SGD.
En vista de lo anterior, los autores de este artículo desarrollan un proyecto de investigación doctoral que busca aportar elementos para comprender y promover procesos de aprendizaje del saber acerca de la enseñanza de las construcciones euclidianas (un tipo particular de construcciones con regla y compás) realizadas con el software GeoGebra en contextos de formación inicial de profesores de matemáticas, con una perspectiva educativa de corte histórico-cultural. En el marco de tal proyecto, el presente artículo tiene el propósito de destacar cómo una determinada concepción del aprendizaje humano da forma al diseño de un entorno de aprendizaje centrado en las construcciones euclidianas con GeoGebra y dirigido a futuros profesores de matemáticas. Para esto, se describen los referentes teóricos/metodológicos y los elementos que han estructurado el diseño del entorno de aprendizaje.
2. REFERENTES TEÓRICOS DEL DISEÑO
El diseño del entorno de aprendizaje se fundamenta en los conceptos de saber, aprendizaje y actividad, tal como estos se presentan en la Teoría de la Objetivación (TO), una perspectiva educativa de corte histórico-cultural comprometida con “la creación dialéctica de sujetos reflexivos y éticos que se posicionan críticamente en prácticas matemáticas constituidas histórica y culturalmente, y que reflexionan sobre nuevas posibilidades de acción y pensamiento” (Radford, 2020a, p. 34). En lo que sigue, se definen estos tres conceptos y se relacionan con las características del contexto en el que se enmarca el entorno de aprendizaje.
2.1. SABER / SABER DOCENTE
En la TO, el saber se define como “un sistema codificado de procesos corpóreos, sensibles y materiales de acción y de reflexión, constituidos histórica y culturalmente” (Radford, 2017a, p. 101). Desde esta perspectiva, el saber es el producto de laboriosos e inacabados procesos históricos de refinamiento, codificación y expansión de determinadas formas culturales de expresión, acción y pensamiento. Para Radford (2017a), el saber aparece en un contexto específico y a través de un problema particular, como resultado de su puesta en movimiento, lo que implica materializarse en la forma de un conocimiento. En otras palabras, el conocimiento es “el contenido conceptual concreto en el que se manifiesta o actualiza o materializa o encarna el saber. Su contenido conceptual concreto aparece y puede aparecer únicamente en una actividad -la actividad que media el saber y el conocimiento” (p. 109).
Desde esta perspectiva, el saber docente se asume como un sistema de procesos corpóreos, sensibles y materiales de acción y reflexión (siempre en movimiento), que existen y son reconocidos en la cultura académica universitaria como necesarios por cuanto permiten a los futuros profesores reafirmarse (y constituirse) como sujetos docentes a través de la enseñanza. Que el saber docente se encuentre en constante movimiento significa que, como todo saber cultural, el saber docente “cambia de cultura en cultura y con el paso del tiempo” (Radford, 2020a, p. 34). En este sentido, el carácter temporal, plural, heterogéneo y situado del saber docente contrasta con “los ideales de racionalidad y objetividad que han marcado, durante mucho tiempo, las pautas de algunos especialistas en planes y políticas dirigidas a los docentes” (Xavier, 2014, p. 831).
En cuanto a lo específico del saber docente, Tardif (2002) le considera como “un saber plural, formado por una amalgama, más o menos coherente, de saberes procedentes de la formación profesional y disciplinarios, curriculares y experienciales” (p. 29). Para este investigador, el saber docente es movilizado por el profesor durante el trabajo con sus alumnos en el aula y, de manera más general, dentro de la escuela. Por saber profesional se entiende aquel saber producido por las ciencias de la educación (p. ej., la educación matemática) y difundido por las instituciones de formación del profesorado; mientras que por saber disciplinario se entiende aquel producido por la tradición cultural y seleccionado por las instituciones de formación para su difusión a través de cursos o asignaturas (Tardif, 2002).
2.2. APRENDIZAJE
La TO considera el aprendizaje como el encuentro de los individuos con el saber histórico y cultural (p. ej., el saber matemático, pedagógico, estético); un saber que objeta al individuo en su encuentro, es decir, le opone resistencia. Para hacer operativa esta noción, Radford (2017b) conceptualiza el aprendizaje como procesos de objetivación, esto es, como procesos sociales, corporales, materiales y simbólicos de:
[...] volverse, progresivamente y críticamente, consciente de una forma codificada de pensamiento y de acción -algo que notamos gradualmente y al mismo tiempo adquiere significado. Son procesos de objetivación aquellos actos de notar significativamente algo que se revela a la conciencia por medio de nuestra actividad corpórea, sensorial y artefactual. (Radford, 2017b, p. 121)
En este artículo, los procesos de objetivación se entienden como actos progresivos de toma de conciencia de un determinado saber docente en el decurso de una actividad formativa concreta que es, además, una actividad social, corpórea, sensorial y artefactual. Para la TO, la toma de conciencia constituye la forma específicamente humana en que cada individuo reconoce los objetos de su cultura (en particular, el saber) y se posiciona críticamente ante tales objetos. En consecuencia, la toma de conciencia de un saber docente puede verse como el acto subjetivo, emocional y afectivo de reflexión y discernimiento sobre las formas de expresión, acción y pensamiento que constituyen dicho saber. En este acto se forman “sensibilidades culturales para ponderar, reflexionar, comprender, disentir, objetar y sentir a los otros, a nosotros mismos y a nuestro mundo” (Radford, 2017b, p. 122), las cuales permiten al futuro profesor orientarse en la formación, por ejemplo, para producir construcciones euclidianas con GeoGebra o involucrarse responsablemente en las experiencias de producción de estas construcciones de sus demás compañeros.
2.3. ACTIVIDAD / ACTIVIDAD FORMATIVA
La TO plantea que la transformación de un saber en objeto de conciencia requiere de una actividad sensual3 y práctica que ponga en movimiento este saber (Radford, 2020b). La actividad es la categoría ontológica y epistemológica fundamental de la TO para entender el modo específico en que los individuos se expresan, actúan y reflexionan. Para destacar el carácter de espacio de producción humana que es inherente a la actividad del aula, la TO se refiere a esta categoría como labor conjunta, definiéndola como “una forma de vida, algo orgánico y sistémico, un evento creado por una búsqueda común -es decir una búsqueda con otros- de la solución a un problema planteado, búsqueda que es al mismo tiempo cognitiva, emocional y ética” (Radford, 2017b, p. 125).
A partir de estos referentes, la actividad formativa se asume como la forma social, corpórea, sensorial y artefactual de labor conjunta mediante la cual el formador y los futuros profesores se implican mutuamente en una búsqueda de respuestas a problemas (o tareas) que orientan sus acciones al logro de un fin. De esta manera, la actividad formativa puede transformar las condiciones iniciales de una realidad (p. ej., un procedimiento particular de construcción de un triángulo con GeoGebra, conocidos un vértice y el tamaño de dos lados) en la búsqueda de su comprensión y, con ello, hacer posible la toma de conciencia progresiva del saber puesto en movimiento. En consecuencia, el producto de la labor conjunta del formador y los futuros profesores (la obra común) constituye tanto la forma material que adquiere el saber en la realidad concreta (a través de acciones y reflexiones), como el reflejo del saber en la conciencia de quienes producen la obra. Sobre esto último, Leontiev (1978, p. 123) afirma que “la actividad del hombre es lo que constituye la sustancia de su conciencia”.
Un aspecto importante de la labor conjunta se refiere a los recursos semióticos empleados por los individuos para producir la obra común. Estos recursos son consustanciales al pensamiento humano y se materializan a través del cuerpo (acciones cinestésicas, gestos y sensaciones), del uso de signos (lenguaje natural o simbólico) y de artefactos culturales (materiales concretos) (Radford et al., 2009). Con respecto a los artefactos culturales, estos no son neutrales. Al contrario, por ser inseparables de la actividad humana, los artefactos portan significados históricos y culturales que afectan inevitablemente las formas en que los individuos actúan y reflexionan durante la labor conjunta (Radford, 2014).
3. REFERENTES METODOLÓGICOS DEL DISEÑO
El diseño del entorno de aprendizaje es parte de un Experimento de Enseñanza (EE) que busca analizar las condiciones de producción de procesos de objetivación del saber acerca de las construcciones euclidianas con GeoGebra, producidas por futuros profesores de matemáticas chilenos en los últimos años de su carrera universitaria. Aunque este trabajo no se focaliza en el EE, es importante comentar brevemente en qué consisten estos estudios y, particularmente, la fase de diseño del entorno de aprendizaje.
Por EE se entiende el tipo de investigación de diseño (Design-Based Research) usado en la Educación Matemática para analizar la dinámica de actividades instruccionales, con el propósito de producir modelos locales de aprendizaje de los saberes puestos en movimiento (Steffe y Thompson, 2000). Según Barab y Squire (2004, p. 2), la investigación de diseño “no es tanto un enfoque, sino una serie de enfoques, con la intención de producir nuevas teorías, artefactos y prácticas que tengan en cuenta y potencialmente impacten el aprendizaje y la enseñanza en entornos naturalistas”. En las últimas décadas, los EE han ganado terreno en la investigación sobre el aprendizaje de futuros profesores de matemáticas en sus espacios naturales de producción social (Molina et al., 2011).
Por lo anterior, el EE en el que se enmarca este artículo fue pensado tanto para producir un modelo local de aprendizaje del saber acerca de las construcciones euclidianas con GeoGebra por futuros profesores de matemáticas, como para validar este modelo desde la evidencia empírica recolectada en diferentes programas de formación inicial del profesorado en Chile y la consecuente mejora de las actividades formativas del experimento.
La realización del EE contempla tres fases de investigación: diseño instruccional, implementación y análisis retrospectivo (Gravemeijer, 2004; Simon, 2000). En atención al propósito del artículo, seguidamente se explica en qué consiste la fase de diseño instruccional.
3.1. DISEÑO INSTRUCCIONAL
Por lo general, la fase de diseño instruccional consiste en la elaboración de un entorno de aprendizaje y la respectiva justificación. En este artículo, el entorno de aprendizaje se entiende como la “conjunción de las tareas diseñadas y la concepción de una determinada manera de usarlas, incluyendo el papel del formador de profesores y los documentos adicionales” (Llinares, 2004, pp. 97-98). Visto así, el diseño del entorno pone especial atención en las tareas de formación y en las interacciones entre el formador y los futuros profesores con las tareas y los recursos semióticos empleados para resolverlas. En sintonía con los referentes teóricos, estos elementos del diseño (tareas e interacciones) se corresponden con determinados saberes por movilizar, un motivo-objetivo y unas metas.
Teniendo en cuenta los referentes teóricos y metodológicos expuestos, en el próximo apartado se describen los elementos que estructuran el diseño del entorno de aprendizaje.
4. ELEMENTOS DEL DISEÑO
A partir de la concepción de actividad formativa, en este trabajo los elementos que estructuran el diseño del entorno de aprendizaje incluyen el saber docente movilizado (lo que da lugar al contenido de la formación), el motivo, objetivo y metas de la actividad formativa, las tareas de la formación y las interacciones.
4.1. EL SABER DOCENTE POR MOVILIZAR
Por medio de la implementación del entorno de aprendizaje se busca poner en movimiento un saber docente enraizado en el trabajo que realizan los profesores de matemáticas de educación básica y media de Chile, cuando enseñan las construcciones euclidianas haciendo uso del software GeoGebra. En este artículo, dicho saber se denomina: Saber Acerca de las Construcciones Euclidianas con GeoGebra (SACEG). Aunque se admite que el SACEG, como todo saber docente, puede nutrirse de saberes provenientes de distintas fuentes, en el diseño se asume que dicho saber se alimenta de saberes disciplinarios y profesionales específicos de la formación inicial del profesorado de matemáticas.
La vertiente disciplinaria
En cuanto a la vertiente disciplinaria, el SACEG se alimenta de ciertos procesos corpóreos, sensibles y materiales de acción y reflexión geométrica sobre las construcciones con regla y compás, movilizados en los cursos de formación inicial sobre geometría euclidiana. Siguiendo a Valente (2017), este tipo de cursos aportan al futuro profesor el objeto de enseñanza, es decir, esos contenidos que deberían ser aprendidos para su enseñanza en la escuela. Visto así, el SACEG comprende todo sistema de expresión, acción y pensamiento acerca de los objetos de la geometría plana (p. ej., rectas, ángulos y triángulos), codificado histórica y culturalmente como procedimientos de construcción de estos objetos con regla y compás o software dinámico.
Las raíces de estos procedimientos pueden encontrarse en la Grecia clásica (450-300 a. de C.), cuando la producción de tratados sobre los fundamentos de la geometría hacía parte de una larga tradición de abstracción y sistematización progresiva de todo lo creado por el orden científico (Ríbnikov, 1987; Scriba y Schreiber, 2015). Estos tratados contenían los principales problemas geométricos de la época, entre ellos las construcciones con regla y compás. A través de estos problemas, los matemáticos griegos demostraban la existencia de los objetos geométricos con ciertas propiedades (objetos deseados), partiendo de unas condiciones iniciales (objetos dados) (Rey y Babini, 1985). En la resolución de los problemas se empleaba un método que consistía en describir el procedimiento de construcción con regla y compás del objeto deseado, y demostrar que tal procedimiento entregaba el objeto con las propiedades deseadas (Scriba y Schreiber, 2015). Este método fue adoptado por Euclides en su famoso tratado de geometría llamado Elementos.
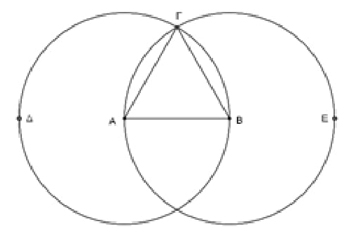
Los Elementos datan del siglo III a. de C. y en el Libro I se presentan los principales problemas de construcción de la época (especialmente, los procedimientos de construcción y las demostraciones asociadas). Por ejemplo, la proposición I.1 enuncia el siguiente problema: Construir un triángulo equilátero sobre una recta finita dada (Euclides, 1991, p. 201). La solución de este problema comienza con la presentación del segmento
La demostración de la proposición I.1 comprende una serie de consecuencias lógicas justificadas por algunos postulados, definiciones o nociones comunes que se citan al inicio de los Elementos. Por ejemplo, en atención al procedimiento de construcción, las operaciones (i) y (ii) se presentan como consecuencia del postulado 3, el cual describe un círculo con cualquier centro y radio; mientras que las operaciones (iii) y (iv) se derivan del postulado 1 que describe el trazado de un segmento de cualquier punto a cualquier punto.
Según Rey y Babini (1985), la función de los postulados en los Elementos era la de “fijar la posibilidad constructiva de las figuras [...] determinando así su existencia y unicidad” (p. 74). De hecho, Euclides asume la posibilidad de dibujar un segmento entre dos puntos dados (Postulado 1), extender el segmento indefinidamente por cualquiera de sus extremos (Postulado 2) y dibujar un círculo con centro y radio dado (Postulado 3), haciendo que todas las proposiciones geométricas, fueran teoremas o construcciones, se fundaran “sobre esas dos figuras y sus relaciones y conexiones mutuas” (Rey y Babini, 1985, p. 52). En consecuencia, la regla y el compás de los griegos, como todo artefacto cultural, portaban contenidos conceptuales específicos que la tradición geométrica había depositado en ellos.
Actualmente, el SACEG se nutre de sofisticadas y evolucionadas definiciones y axiomas de la geometría elemental, de algo más que el método sintético euclídeo para explorar esta geometría (p. ej., el método analítico, originado en el siglo XVII) y de artefactos digitales que hacen posible el trabajo geométrico en el aula de formas novedosas. Con todo esto, los procesos de producción y justificación de construcciones euclidianas elaboradas con GeoGebra caracterizan el SACEG. Para Laborde (1997), las construcciones creadas con SGD (p. ej., con GeoGebra) favorecen el reconocimiento de vínculos entre las evidencias visuales que aportan los dibujos en la pantalla (invarianza de las propiedades espaciales del dibujo) y los hechos geométricos (elementos del sistema axiomático-deductivo de la geometría euclidiana); estos últimos relacionados con ideas que subyacen en las herramientas que ofrece el software.
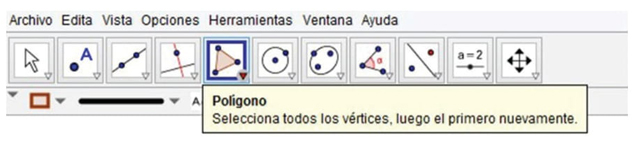
Desde una perspectiva histórica-cultural (Radford, 2014), GeoGebra constituye un artefacto cultural (de naturaleza digital) que proporciona a los usuarios una serie de contenidos conceptuales (herramientas de construcción, medida y otras opciones) y un espacio de trabajo estructurado conceptualmente (apariencias del software) para que ellos experimenten con tales contenidos y produzcan formas novedosas de construir los dibujos dinámicos4 y validar estas construcciones. Por ejemplo, para construir con GeoGebra un triángulo equilátero a partir del tamaño5 de sus lados (equivalente a la cantidad de longitud del segmento m) y de uno de sus vértices (punto P), la herramienta Polígono sugiere un procedimiento guiado por el reconocimiento y/o determinación de los vértices que lo definen (figura 2). La conceptualización que subyace en la herramienta denota la idea moderna de figura geométrica como “el conjunto de sus elementos; el triángulo es “tres puntos del plano”, a los cuales están adheridos tres segmentos y tres ángulos” (Levi, 2006, p. 116).
En el ejemplo, la conceptualización que subyace en la herramienta Polígono y las condiciones iniciales de la figura (m y P) posibilitan el surgimiento de procedimientos de construcción con GeoGebra del triángulo equilátero con consistencia geométrica, los cuales pueden acompañarse de modos de justificar dicha consistencia. Considerando que la incorporación del SGD al aula de matemáticas da lugar a nuevas formas de establecer la verdad de un hecho geométrico (De Villiers, 1998), la justificación de la consistencia geométrica de una construcción con GeoGebra es entendida en este artículo como una parte consustancial de la actividad formativa, manifestada en los modos en que los individuos tratan de persuadir a otros de que el razonamiento en torno al procedimiento de construcción empleado es correcto (Fiallo, 2011).
Desde esta perspectiva, tanto el procedimiento de construcción con GeoGebra del triángulo equilátero como su justificación comprenden formas singulares (conocimientos) del SACEG asociadas al caso de la proposición I.1 de los Elementos. En la práctica concreta, estas formas singulares del SACEG (particularizadas al caso del ejemplo) se manifiestan en acciones orientadas al logro de resultados intermedios que, por sí solos, no satisfacen la necesidad de construir con GeoGebra el triángulo equilátero. De hecho, en líneas generales, las necesidades que mueven a los individuos a realizar una actividad no son satisfechas por los resultados intermedios, sino por el producto de la actividad conjunta de todas las acciones desplegadas (Leontiev, 1978).
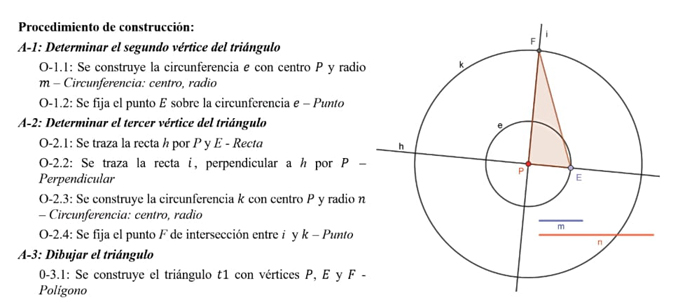
Por lo anterior, las acciones de una construcción con GeoGebra median entre la necesidad de los individuos de producir el dibujo dinámico esperado y las operaciones no conscientes realizadas con el software para lograr las acciones y que se encuentran subordinadas al espacio de trabajo (apariencia Geometría) de GeoGebra. En el ejemplo, una forma singular de construcción del triángulo equilátero puede considerar las acciones: determinar el segundo vértice (A-1), determinar el tercer vértice (A-2), y dibujar el triángulo (A-3); a su vez, cada acción se realiza mediante operaciones (O) con el software que conducen tanto a los resultados intermedios como al dibujo dinámico en su conjunto (figura 3).
Finalmente, el significado que puede atribuirse a las acciones de un procedimiento de construcción con GeoGebra estaría determinado por las relaciones que los futuros profesores establecen entre cada acción y la construcción en su conjunto, de manera tal que la misma acción puede tener un significado distinto en diferentes construcciones de una misma figura. Para tomar conciencia de esta relación, los individuos hacen uso de diversos recursos semióticos que incluyen a GeoGebra, el propio cuerpo (p. ej., los gestos) y los signos (p. ej., el lenguaje natural o simbólico).
En síntesis, el SACEG desde la vertiente disciplinaria expresa la capacidad potencial de los futuros profesores para (i) producir un dibujo dinámico con GeoGebra ajustado al objeto geométrico demandado por una tarea de construcción, (ii) comunicar (de manera oral y/o escrita) el procedimiento de producción del dibujo dinámico en función de acciones y operaciones, y (iii) justificar la consistencia geométrica del dibujo dinámico producido. Esta caracterización es parte de una concepción más amplia del SACEG que se alimenta de una vertiente profesional.
La vertiente profesional
En el aula de matemáticas, el SACEG (en lo que concierne a la vertiente disciplinaria) es objeto de trabajo del profesor, quien busca crear condiciones para su materialización en la práctica concreta. Para cumplir con este objetivo, es necesaria una comprensión del SACEG que asuma la caracterización anterior e incluya otros saberes provenientes de las ciencias de la educación y, particularmente, de la educación matemática. Por lo general, este saber profesional se deriva de estudios sobre el profesor de matemáticas y su práctica docente, cuyas conclusiones luego son incorporadas a los programas de formación inicial.
Para el diseño del entorno de aprendizaje, se ha considerado que el SACEG se alimenta de un saber profesional originado en investigaciones sobre el conocimiento, habilidades y actitudes del profesor de matemáticas. Hiebert et al. (2007) y Mason (2002) se refieren a este saber como la capacidad potencial del profesor para analizar con sentido la enseñanza, en atención al logro de los objetivos de aprendizaje. Siguiendo a Tardif (2002), este tipo de saber refleja un modo particular de relacionarse del profesor con la realidad del aula de matemáticas. En esta realidad, los profesores se tornan en seres sensibles, esto es, “en seres inevitablemente afectados por otras partes de la naturaleza” (Radford, 2018, p. 94), especialmente por los modos en que sus alumnos se expresan, actúan y piensan matemáticamente cuando resuelven problemas matemáticos.
Afectados así, los profesores sienten la necesidad de reconocer en las acciones de sus alumnos ciertos hechos que le atañen (p. ej., una forma histórica y cultural de construcción de un triángulo con GeoGebra) y comprometerse en la transformación de estos hechos, desarrollando la capacidad de mirar con sentido las situaciones de enseñanza y aprendizaje que le atañen (Hiebert et al., 2007; Mason, 2002). Mediante esta capacidad latente, los profesores pueden capturar un hecho tal y como este se presenta en la actividad matemática de sus alumnos (la realidad concreta), al mismo tiempo que va captando los nexos causales y circunstanciales de este hecho en la práctica del aula, y sus contradicciones internas.
Recientemente, la capacidad de mirar con sentido las situaciones de enseñanza y aprendizaje de las matemáticas se ha investigado en ambientes de formación inicial del profesorado y desde distintos enfoques epistemológicos. Por ejemplo, Sherin et al. (2011) se refieren al Teacher Noticing (TN) como la capacidad latente del profesor de lidiar con el conglomerado de datos sensoriales (en constante movimiento) que aparecen ante ellos en la instrucción. Para estos autores, TN involucra dos procesos interrelacionados: (i) prestar atención a hechos particulares del aula y (ii) dotar de sentido a estos eventos.
Sobre el segundo proceso, Van Es y Sherin (2002) sostienen que dotar de sentido es un proceso que implica tanto interpretar lo observado (relacionando los hechos con categorías abstractas y caracterizando lo visto en términos de episodios instruccionales familiares) como tomar decisiones pedagógicas con base en las interpretaciones. Centrados en el pensamiento de los alumnos, Jacobs et al. (2010) vinculan la capacidad TN con el desarrollo de tres procesos interrelacionados: (i) identificar hechos matemáticos relevantes en las respuestas de los estudiantes; (ii) interpretar la comprensión de los estudiantes de los hechos matemáticos y (iii) decidir cómo actuar en función de la comprensión que se tiene de estos hechos.
En este artículo se asume el procedimiento de construcción con GeoGebra y la justificación de su consistencia como la realidad concreta que aporta a la actividad formativa la materia prima (materialización de un hecho geométrico) para desarrollar la capacidad de los futuros profesores de mirar con sentido sus producciones. Desde una perspectiva dialéctica-materialista, los procedimientos de construcción con GeoGebra llevan implícitas contradicciones6 internas (p. ej., las derivadas de las diferencias entre los dibujos dinámicos presentados y las respuestas esperadas por el formador) que, dentro de la actividad formativa, constituyen oportunidades para la toma de conciencia del SACEG en su vertiente profesional. En otras palabras, estudiando las contradicciones inherentes a la producción de construcciones euclidianas con GeoGebra es posible recrear formas de hacer progresar a los futuros profesores en su capacidad para dar sentido a los hechos geométricos asociados con los procedimientos de los demás compañeros. Con esto, se busca sacar provecho de las “situaciones imprevistas durante el desarrollo de la lección que pueden ser usadas para apoyar el aprendizaje de los estudiantes” (Llinares, 2019, p. 31).
En resumen, el SACEG en la vertiente profesional se nutre de la capacidad de mirar con sentido la enseñanza, al estilo de Jacobs et al. (2010), expresándose como procesos sociales que involucran (i) identificar un hecho geométrico en el procedimiento de construcción con GeoGebra realizado por un futuro profesor, (ii) interpretar el modo en que otros comprenden estos hechos, e (iii) intervenir para favorecer el progreso en la comprensión del hecho.
4.2. MOTIVO, OBJETIVO Y METAS
Según Leontiev (1978), toda actividad humana responde a necesidades de los individuos que se involucran en ella, siendo estas necesidades objetivadas en el motivo que impulsa la labor. Desde esta perspectiva, el entorno de aprendizaje descrito aquí tiene por motivo contribuir al desarrollo de las capacidades de los futuros profesores para relacionarse, de manera crítica y ética, con determinados procesos corpóreos, sensibles y materiales de acción y reflexión, característicos del SACEG.
Por su parte, el motivo se encuentra ligado a un objetivo (material o ideal) que le confiere cierta orientación a la actividad. Según Reverand (2004, p. 165), el objetivo “constituye el resultado futuro, anticipado de la actividad, todo aquello que el hombre desea alcanzar, obtener, crear”. En este sentido, la actividad formativa derivada de la implementación del entorno de aprendizaje tiene por objetivo el reconocimiento consciente y progresivo del SACEG a partir de la intervención responsable del formador y los futuros profesores en la labor de producción de procedimientos de construcción con GeoGebra y de formas de justificar la consistencia de estos procedimientos.
Finalmente, ya que “una actividad que se desenvuelve en alguna medida, presupone el logro de una serie de fines concretos” (Leontiev, 1978, p. 84), para que la resolución de una tarea de construcción con GeoGebra se mueva en la dirección de su objetivo, conviene identificar una o más metas que puedan lograrse a través de tareas especialmente elaboradas (Radford, 2017b). En este punto, una meta es la representación consciente del resultado al que se subordinan las acciones, mientras que una tarea comprende la enunciación de una meta que se estipula bajo ciertas condiciones.
A partir de lo anterior, para que la actividad formativa se despliegue en la dirección de su objetivo (el reconocimiento del SACEG), se han definido las siguientes metas:
Resolver tareas que plantean construcciones euclidianas con GeoGebra, cuyas acciones se relacionan con el SACEG desde la vertiente disciplinaria.
Afrontar profesionalmente las contradicciones inherentes a la resolución de tareas de construcción con GeoGebra, cuyas acciones se relaciona con el SACEG desde la vertiente profesional.
4.3. CONTENIDO DE LA ACTIVIDAD FORMATIVA
Como se ha dicho, para que un saber se materialice en la práctica concreta, este debe “mostrarse en sí mismo en la actividad a través de la cual este adquiere su contenido” (Radford, 2017a, p. 108). Para el diseño del entorno de aprendizaje se ha asumido que el contenido de las actividades formativas viene dado por la materialización del SACEG en la obra común del formador y los futuros profesores. Por tratarse de actividades mediadas por tareas, el modo en que el SACEG aparece en lo concreto (desde lo disciplinario) se relaciona con el contenido conceptual de la tarea.
4.4. TAREAS Y RECURSOS
Las tareas del entorno de aprendizaje (llamadas tareas de construcción con GeoGebra) se consideraron consustanciales de la actividad formativa en cuanto aportan las condiciones iniciales para que los futuros profesores configuren su experiencia con el saber involucrado en la actividad y comprendan la naturaleza del trabajo docente en geometría (Watson y Ohtani, 2015). En cada actividad formativa, la tarea asociada tiene el propósito de orientar las acciones de los individuos hacia el logro de las metas.
En total, se incorporaron 16 tareas de construcción con GeoGebra al entorno de aprendizaje. Todas se corresponden con las clásicas tareas de producción de Cabri-dibujos,7 las cuales demandan la construcción de dibujos dinámicos representativos de objetos geométricos dados mediante descripción verbal. Según Laborde (1997), mediante esta clase de tareas es posible producir:
(...) un dibujo en la pantalla que conserve ciertas propiedades espaciales impuestas cuando se desplace uno de los puntos básicos del dibujo. La tarea para el alumno consiste, por tanto, en elaborar un procedimiento de producción del Cabri-dibujo, basado en las primitivas geométricas disponibles. (Laborde, 1997, p. 42)
El contenido conceptual de las tareas del entorno se determinó a partir de la caracterización del SACEG (antes descrita) y del análisis de un grupo de proposiciones tomadas de ciertas obras de geometría.8 Se seleccionaron 17 proposiciones (problemas de construcción con regla y compás) según la relevancia histórica del problema en función de su presencia directa o indirecta en el currículo de matemáticas chileno. A partir de estas proposiciones, se elaboraron 16 tareas de construcción (tabla 1), 7 referidas a rectas notables, ángulos, triángulos y cuadriláteros, y 9 referidas a la división de segmentos en una razón dada, usando la concepción euclidiana de razón y proporción.
Tabla 1 Proposiciones seleccionadas para la elaboración de las tareas
| Fuente | Proposiciones |
|---|---|
| Libros I, II y IV de los Elementos (Euclides, 1991) | I.1, I.9, I.10, I.12, II.1, IV.10 |
| Libro VI de los Elementos (Euclides, 1994) | VI.9, VI.11, VI.12*, VI.13, VI.16*, VI.30 |
| Libros I, II y VI (Tratado III, Tomo I) del Compendio Mathematico (Tosca, 1757) | I.9, II.1, II.2, II.4, VI.5 |
(*) Estas proposiciones dieron lugar a la misma tarea de construcción.
El análisis de las proposiciones también aportó información sobre la solución de estos problemas, incluyendo los pasos de construcción con regla y compás sugeridos, el dibujo geométrico asociado y la demostración de la validez de cada construcción. Con esta información se procedió a formular los enunciados de las tareas de construcción con GeoGebra y establecer algunas posibles respuestas. La información recabada por cada proposición se organizó en cuadros similares al mostrado en la figura 4.
La información anterior permitió revelar los procedimientos de construcción (teoría geométrica) evocados en las respuestas de cada proposición, así como determinados signos y artefactos (sistemas semióticos) que se ofrecen a los individuos para poder expresarse, actuar y pensar sobre la teoría geométrica. Por ejemplo, la información de la figura 4 expresa procedimientos prototípicos o ideales de resolución del problema de dividir un ángulo dado en dos partes iguales, usando regla y compás (proposición I.9). En el contexto escolar chileno, este problema equivale a construir la bisectriz de un ángulo dado, en cuyo procedimiento los alumnos despliegan un repertorio de signos (dibujos, notación simbólica y marcas) y artefactos (teoría geométrica, lenguaje escrito e instrumentos de construcción), altamente sofisticados, que entran en juego para significar la idea de bisectriz de un ángulo como el rayo que biseca al ángulo.
El enunciado de una tarea de construcción con GeoGebra incluye la referencia al objeto geométrico a ser construido, unas preguntas orientadoras y una hoja de trabajo (archivo .ggb) con las condiciones iniciales de la construcción y sobre la cual se deben producir los dibujos dinámicos. Estos enunciados siguen la misma estructura de las proposiciones en las obras consultadas (enunciado, hipótesis y tesis), reduciendo el caso general a un caso particular cuyos elementos dados se muestran en la hoja de trabajo. A modo de ejemplo, la figura 5 muestra la tarea GGB-4b, asociada a la proposición II.2 de Tosca (1757).
Junto con la elaboración de las tareas de construcción con GeoGebra, se establecieron posibles respuestas considerando que la aplicación de cada tarea podía dar lugar a dos formas de obra común estrechamente vinculadas, en cuya producción el formador y los futuros profesores se encuentran con el SACEG.
La primera forma de obra común aparece en la actividad formativa como respuesta directa a las preguntas de las tareas de construcción con GeoGebra, y contiene: (i) el dibujo dinámico esperado, (ii) la comunicación (oral y/o escrita) del procedimiento de construcción del dibujo, y (iii) la justificación de su consistencia geométrica. Estas componentes de la respuesta a una tarea de construcción fueron anticipadas mediante el análisis de la información correspondiente al postulado que originó la tarea.
Por ejemplo, el análisis de la información asociada a la proposición II.2 (figura 5) permitió identificar dos casos posibles de construcción del triángulo rectángulo, según la posición que ocupan los objetos dados (lados del triángulo) en el dibujo. Claro está, la funcionalidad del software utilizado (como editor gráfico) y la variedad de contenidos conceptuales que este ofrece convierte la resolución de una tarea de construcción con GeoGebra en una oportunidad para ampliar el campo de experimentación posible con los dibujos dinámicos (Laborde, 1997). En el caso de la tarea GGB-4b, la proposición II.2 puede sugerir un procedimiento de construcción para el cual m y n representan los tamaños de los catetos del triángulo (caso 1 de II.2). Al relacionar este procedimiento con la conceptualización de la herramienta Polígono (usada en este caso para producir el dibujo dinámico) es posible organizar la construcción en acciones y operaciones, según se muestra en la figura 6.
En cuanto a la comunicación del procedimiento de construcción (pregunta b de la tarea), se espera que los futuros profesores justifiquen la consistencia (o no) de la construcción realizada, esto es, que formulen un discurso argumentativo que valide el procedimiento de construcción empleado, situando tal procedimiento dentro del marco axiomático asociado a la proposición que origina la tarea. En el espacio de trabajo del software, la relación con la teoría geométrica puede lograrse a partir de la identificación de propiedades del dibujo dinámico que se mantienen (o no) invariantes tras ser arrastrado por sus elementos libres. Ya que la producción del dibujo dinámico es mediada por GeoGebra, lo que importa de la argumentación aquí no es la secuencia proposicional de deducciones características de una demostración formal escrita, sino la justificación razonada de lo obtenido en atención a la teoría geométrica (Sinclair y Robutti, 2013).
Antes de explicar la segunda forma de obra común, conviene recordar que la resolución de cada tarea de construcción con GeoGebra lleva implícitas contradicciones internas que pueden ser reconocidas y trascendidas por causa de la labor conjunta del formador y los futuros profesores. Por esta razón, se espera que la segunda forma de obra común aparezca en la actividad formativa como un modo específico de intervención del futuro profesor motivada por alguna contradicción presente en la respuesta de otro compañero a la tarea de construcción que se trate. En lo específico, este tipo de obra común implica: (i) identificar un hecho geométrico de la construcción que permita explicar la contradicción presente en la respuesta del compañero, (ii) interpretar el modo en que los otros entienden este hecho geométrico, e (iii) intervenir como profesor para ayudar a que otros mejoren su comprensión del hecho geométrico (avanzar para superar la contradicción).
A modo de ejemplo, se presenta el caso hipotético de Gonzalo y Layla, dos futuros profesores que se involucran en la resolución de la tarea GGB-4b de la figura 5. En un momento de la actividad formativa, Layla expone ante el formador y los demás compañeros su respuesta a la tarea de construcción, mientras que Gonzalo se va dando cuenta de que la joven ha empleado un procedimiento de construcción distinto al suyo (figura 7). En la respuesta de Layla, Gonzalo reconoce la forma de construcción del triángulo rectángulo para el cual el tamaño de la hipotenusa es n (este hecho se corresponde con el caso 2 de la proposición II.2), y se percata que la circunferencia h (operación 2 del procedimiento) no contribuye con la localización del tercer vértice del triángulo. En este ejemplo, las operaciones que producen el tercer vértice del triángulo constituyen un hecho geométrico, mientras que la circunferencia h se convierte en el foco de la contradicción.
Para hacer que Layla reconozca la contradicción en su respuesta y la supere, Gonzalo sugiere que se revisen las operaciones del procedimiento de construcción y se organicen dichas operaciones en acciones, atendiendo a la conceptualización de la herramienta Polígono, usada por Layla para dibujar el triángulo. Por ejemplo, las operaciones 1 y 3 de la figura 7 permiten determinar el vértice E del triángulo (primera acción), mientras que las operaciones 4, 5, 6 y 7 permiten la localización del vértice I (segunda acción). De esta manera (organizando las operaciones en acciones) se crean las condiciones para el cuestionamiento del papel que desempeña la operación 2 en la construcción.
Mientras esto se produce, Gonzalo podría intervenir formulando preguntas (p. ej., ¿qué herramienta del GeoGebra te permitió construir el triángulo?, ¿cuáles son los requerimientos de esta herramienta para ser usada?) con las cuales él busca dirigir la atención de Layla hacia los objetos que permiten determinar los vértices E e I, necesarios para el empleo de la herramienta.
4.5. INTERACCIONES
Dado que el aprendizaje del SACEG es un fenómeno social, las interacciones entre el formador y los futuros profesores durante los encuentros representan un aspecto crucial del entorno de aprendizaje. Se tiene previsto que la aplicación de cada tarea se haga siguiendo un ciclo de trabajo colaborativo inspirado en los momentos de la actividad del aula que propone Radford (2017b). La figura 8 muestra los cuatro momentos que conforman el ciclo de resolución de una tarea de construcción con GeoGebra, ajustados al tiempo de duración del encuentro, la cantidad de tareas atendidas y las características del espacio físico.
En el momento de presentación de la tarea, el formador muestra y explica la tarea a los futuros profesores, procurando que ellos entiendan lo que deben hacer. En ocasiones, será necesario despejar aquellas dudas iniciales que puedan interferir en el desarrollo del siguiente momento. Durante la búsqueda de respuestas, los futuros profesores trabajan de manera independiente o en pequeños equipos (según las condiciones del encuentro) para producir respuestas posibles a la tarea presentada.
Para el momento de discusiones en pequeños grupos, el formador ofrece la debida retroalimentación, responde las dudas que van surgiendo, hace preguntas y estimula la búsqueda de respuestas. Además, el formador se esfuerza por reconocer las oportunidades de aprendizaje del SACEG en los modos de resolución de la tarea que surgen durante un momento de la búsqueda, identificando las respuestas que merecen ser discutidas con todo el grupo y los signos de incomprensión o frustración que impiden el avance hacia la obra común. Al centrar la atención en estas cuestiones se aumentan las posibilidades de alcanzar las metas de la formación, ya que las respuestas detectadas por el formador se convierten en la materia prima para el siguiente momento del ciclo.
Luego de decidir las respuestas que serán compartidas y el orden de intervención en que serán compartidas, el formador pone en marcha la discusión en gran grupo. En este momento, se pide intencionalmente a los futuros profesores que presenten sus obras (completas o inconclusas) al resto del grupo, promoviendo el diálogo sobre ideas geométricas importantes (Stein et al., 2008) para la situación de resolución en que se encuentren. Normalmente, este momento se desarrolla en dos instantes. El primer instante es de reconocimiento de las condiciones de la producción de la respuesta que es compartida. En este instante el formador intenta que los futuros profesores reconozcan las potencialidades y limitaciones9 de la construcción que se les presenta, para lo cual se podría optar por solicitar a quien la comparte que reproduzca el procedimiento de construcción en la hoja de trabajo, desde la primera operación realizada.
El segundo instante es de modificación de la respuesta. En este instante el formador invita a los presentes a comprometerse en la transformación de las condiciones iniciales de producción de la respuesta compartida, ofreciendo la ayuda necesaria para superar las limitaciones de la construcción. Este acto demanda la movilización del SACEG para el caso de la tarea que se trate, de manera que los esfuerzos mancomunados favorecen el reconocimiento de aquello que necesita ser modificado, ya sea en la construcción misma (el dibujo dinámico) o en la forma de comunicar y/o probar la consistencia del procedimiento de construcción.
Para que un futuro profesor se sienta desafiado a actuar profesionalmente, el formador le ofrece opciones de intervención a través de preguntas específicas, tales como: ¿Encuentras alguna diferencia importante entre esta respuesta y la tuya? ¿Dónde está el problema en la respuesta? ¿De qué manera puedes actuar como profesor para lograr que tu compañero reconozca este problema y lo supere?
El rol del formador en los momentos antes descritos se corresponde con un rol ético (Radford, 2020b), en el sentido de reconocerse como inseparable de la actividad formativa que media y actualiza el SACEG. En otras palabras, el formador actúa éticamente en la actividad al asumirse dentro de una conciencia colectiva en la búsqueda de la obra común, problematizando la relación de los futuros profesores con el SACEG, abonando el camino hacia el logro de las metas de la formación y aportando a la labor conjunta sus formas idiosincráticas de expresión, acción y pensamiento como un profesor de matemáticas más, dentro de un marco de actuación profesional éticamente responsable.
Se tiene previsto que la aplicación de las tareas se realice por encuentros con los futuros profesores, de 90-120 minutos de duración. Bajo condiciones ideales, se requieren 10 encuentros para aplicar las tareas, a los que se anteponen dos encuentros destinados a discutir sobre la resolución de tareas de construcción geométrica con software dinámico y la elaboración de narrativas como herramienta de formación profesional.
CONSIDERACIONES FINALES
Se describieron los referentes teóricos/metodológicos y los elementos que conformaron el diseño de un entorno de aprendizaje centrado en el saber acerca de las construcciones euclidianas con GeoGebra. Tal descripción es una respuesta a la necesidad de los autores de mostrar cómo una determinada concepción del aprendizaje humano puede dar forma al diseño de un entorno de aprendizaje centrado en las construcciones euclidianas con GeoGebra y dirigido a futuros profesores de matemáticas chilenos, próximos a egresar. Desde una perspectiva histórica-cultural del aprendizaje, se procuraron las condiciones para el encuentro progresivo de futuros profesores con el SACEG. En particular, el hecho de asumir el aprendizaje del SACEG como procesos de objetivación ha supuesto el reto de pensar en la naturaleza y fuentes del SACEG como saber docente.
Por otro lado, la concepción de actividad adoptada permitió que la actividad formativa se proyectara como un espacio legítimo de toma de conciencia del SACEG, en sus vertientes disciplinaria y profesional. Una ventaja de la actividad formativa que se propone es la posibilidad de ser integrada parcial o totalmente a la dinámica de funcionamiento de las carreras de Pedagogía en Matemáticas del país ya sea como curso optativo, unidad de aprendizaje o actividad de mejoramiento. Finalmente, el camino recorrido ofrece un acercamiento a lo que implica asumir algunos principios de la Teoría de la Objetivación para diseñar un entorno de aprendizaje dirigido a futuros profesores de matemáticas, estableciendo con ello un puente entre la formación inicial y el mundo de la enseñanza.











 nueva página del texto (beta)
nueva página del texto (beta)