1. INTRODUCCIÓN
Las dificultades para transitar de un pensamiento aritmético hacia el algebraico reportadas en las últimas décadas del siglo xx (Matz, 1980; Herscovics y Kieran, 1980; Booth 1982, 1988; Filloy y Rojano 1984, 1989; Lodholz, 1990; Herscovics y Linchevski, 1994, entre otros), proporcionaron referentes para investigar el desarrollo del pensamiento algebraico desde edades tempranas, en la expectativa de contribuir a una transición adecuada hacia el estudio formal del álgebra.
Las actividades de generalización son consideradas promotoras del razonamiento algebraico en edades tempranas (Kieran, 2004; Kaput, 2008). En este trabajo, se parte de la premisa que, expresar la generalidad es un proceso que contribuye al desarrollo y adquisición del lenguaje algebraico. De modo que, cuando los estudiantes comunican las regularidades que observan en tareas matemáticas de generalización, es referencia del trabajo algebraico, aún principiante, que ellos producen (Mason et al., 1999). Ciertamente, en álgebra resulta relevante la expresión general y la manipulación matemática de dicha expresión.
Existen diferentes tareas matemáticas para promover el desarrollo de la generalización algebraica en edades tempranas y, motivar a través de ellas las expresiones de generalización. En la primera etapa de esta investigación se proponen la resolución de secuencias figurales-numéricas y numéricas.
1.1. Secuencias y patrones
Una secuencia es un conjunto de elementos ordenados mediante un patrón o relación. Hay dos clases de secuencias que suelen explorarse en edades tempranas para propiciar la generalización: aquellas que se conforman de patrones de repetición y las que se conforman de patrones de crecimiento (Warren, 2005; Warren y Cooper, 2006; Rivera, 2013). Un patrón de repetición se concibe como aquella unidad discernible de repetición. La repetición del patrón forma la secuencia, es decir, la secuencia tiene una estructura cíclica que puede generarse por la aplicación repetida del patrón. Las secuencias que suelen trabajarse con escolares pequeños (principalmente de 5 a 8 años) son figurales, mayormente geométricas, un ejemplo de ello se puede apreciar en la figura 1.

Figura 1 Secuencia conformada por un patrón de repetición geométrico, presentada en Rittle-Johnson et al. (2013).
Este tipo de secuencias permite guiar a los estudiantes a moverse en un solo conjunto de elementos; conduciéndoles a distinguir la unidad de repetición (patrón); crear nuevas secuencias con la misma regla estructural; extender o continuar las secuencias agregando una o más unidades de repetición; o completar la parte faltante de la secuencia (al remover algunas piezas para que el estudiante las coloque acorde con la unidad de repetición). También, es posible mediante este tipo de secuencias encauzar a los estudiantes a establecer relaciones entre dos conjuntos, pero para ello se requiere mayor intervención docente.
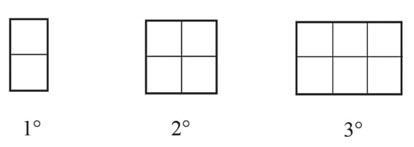
Las secuencias que involucran patrones de crecimiento se caracterizan por tener unidades distinguibles llamadas términos y cada término depende del anterior o del valor numérico de la posición (Queensland Studies Authority, 2005). Pueden ser figurales o numéricas, los términos aumentan de forma progresiva siguiendo una determinada regla que establece el crecimiento. Tienen un nivel de dificultad mayor que las secuencias que involucran patrones de repetición. Dependiendo de la complejidad de la regla se incrementa la dificultad para resolverlas (Zapatera, 2018). En la figura 2 se presenta un ejemplo de secuencia figural o geométrica, creciente (aumenta de forma progresiva) y lineal (porque la regla que lo rige es 2n). Este tipo de secuencias es factible de resolver por estudiantes de educación básica, de 9 a 12 años.
Las secuencias figurales son de interés en diversas investigaciones (Carraher et al., 2008; Böttinger y Söbbeke, 2009; Cañadas et al., 2016) porque se considera que ciertos patrones visuales permiten identificar las características que conducen a la generalización del patrón, incluso, permiten trabajar con expresiones equivalentes (Lee y Freiman, 2006; Villa, 2006; Rivera et al., 2007). Sin embargo, se reconoce que no cualquier forma visual es factible de expresar, de manera inmediata, aquello que se desea generalizar.
En cuanto a las secuencias numéricas, el trabajo en edades tempranas se centra primero en encontrar el siguiente número de la secuencia y los estudiantes suelen hallarlo basándose del número anterior (Wilkie, 2014). Se reconoce que para encontrar una regla de generalización es necesario poner en juego otro tipo de habilidades visuales, así como habilidades numéricas y de abstracción (Villa, 2006).
Cuando se trabaja con secuencias, sean figurales o numéricas, es importante
considerar que los estudiantes puedan conjeturar una regla verdadera con los
conocimientos previos que poseen, debido a que ninguna secuencia finita de
elementos genera de manera única el siguiente término, por ejemplo, en la
secuencia numérica 1, 2, 3, 4, 5, 6… el siguiente término puede ser 7 si la
secuencia es definida por
Adicionalmente, autores como Radford (1996) hacen énfasis en no confundir las generalizaciones algebraicas con otras formas de tratar lo general y sugieren que los estudiantes se involucren con tareas matemáticas de carácter algebraico. De manera análoga, las secuencias que considera Rivera (2013, 2015) en sus investigaciones competen a aquellas que promueven estructuras sobre relaciones matemáticas o alguna otra estructura matemática. Rivera menciona que todas las estructuras deben ser coherentes, generales y precisas. Coherentes en el sentido de que una sola regla determine todos los resultados necesarios (se interpreta para los escolares en edades tempranas aquella regla factible); generales, porque pueden explicar el mayor número de términos posibles; y precisas en el entendido de que es posible predecir, hipotéticamente, un término respecto al término real. Siempre que sea posible se debe trabajar con estructuras simples. Cuando Rivera alude a generalización al trabajar con secuencias figurales, se refiere tanto a las prácticas matemáticas de construcción como a la justificación de fórmulas directas.
1.2. Expresiones de generalización
Existen diferentes aspectos de interés en el contexto de la generalización algebraica cuando se trabajan secuencias figurales o numéricas. Por ejemplo, algunas investigaciones tienen interés en el desarrollo del pensamiento funcional (Brizuela y Blanton, 2014; Cañadas et al., 2016); otras se enfocan en las estrategias que utilizan los estudiantes al generalizar (Stacey, 1989; Warren 2005; Warren y Cooper, 2007); o en las estrategias y formas de pensamiento algebraico (Callejo et al., 2016); o en las formas del pensamiento algebraico y los recursos semióticos que son movilizados por los estudiantes cuando se enfrentan a la solución de secuencias figurales o numéricas (Radford 2010a, 2010b; Vergel, 2013, 2015).
En esta investigación es de particular interés, además del proceso de generalización, el alcance de la generalización algebraica en las expresiones de generalización que producen los estudiantes en diferentes tareas matemáticas de generalización. En este documento se reporta lo acontecido en las tareas de generalización que compete a secuencias figurales-numéricas y numéricas, pero el trabajo de investigación considera también otro tipo de tareas matemáticas.
Una característica del lenguaje algebraico es el simbolismo alfanumérico, cualidad que resulta de interés en algunas investigaciones con estudiantes de edades tempranas, especialmente el uso de la notación algebraica. En los trabajos de investigación del grupo de investigadores conformado por Schliemann et al. (2011, 2012) se distingue el uso temprano de notación algebraica (uso de letras para representar cantidades incógnitas y variables) en virtud de que consideran que dicha notación influye en el aprendizaje del álgebra y; aunque los estudiantes suelen presentar dificultades, los autores argumentan que la transición del lenguaje natural a la notación simbólica no es tan difícil si los estudiantes ya perciben y entienden las cantidades variables que son representadas. Radford (2018) también sugiere un simbolismo que incluye al alfanumérico, aunque también involucra los sistemas semióticos no convencionales, como el lenguaje natural, los gestos, el ritmo y otros recursos semióticos a través de los cuales considera que los estudiantes dan significado a la generalidad algebraica.
Sin embargo, para promover el simbolismo alfanumérico se hace necesaria la intervención del docente quien introduce el uso de letras y orienta su significado (Blanton y Kaput, 2004; Radford, 2010a; 2018; Carraher et al., 2013), ya que pasar de una notación aritmética a una notación algebraica implica un cambio conceptual que requiere ser desarrollado paulatinamente. Asimismo, cuando los estudiantes no tienen experiencias en percibir cantidades variables o usar símbolos que representen esas cantidades variables es difícil que puedan atribuir, de manera espontánea, literales para representar sus expresiones de generalización.
Aunque se comparte la postura de que una notación alfanumérica es característica del lenguaje algebraico, esta investigación no hace énfasis en dicha notación, sino en las expresiones primitivas de generalización algebraica que producen los estudiantes en formato escrito y verbal, con base en los conocimientos de aritmética adquiridos durante sus cursos escolares previos y sin haber recibido un entrenamiento en tareas de generalización.
De acuerdo con Mason, Graham y Johnston-Wilder (2005), cada estudiante desde que inicia la escuela tiene la capacidad de abstraer y generalizar a partir de casos particulares. De modo que, resulta de gran importancia orientar esa cualidad hacia la generalización matemática (Mason, 1996) y lograr que la usen y desarrollen en un contexto de números y relaciones, dando lugar al pensamiento algebraico (Mason, 2014). Asimismo, para las expresiones de generalización se debe permitir que fluya el lenguaje natural antes de introducir cualquier notación externa, y tratar de interpretar aquellas generalizaciones primitivas que los estudiantes expresan como punto de referencia para promover la notación alfanumérica.
A partir de lo referido, el propósito de la investigación es analizar el proceso de generalización y las expresiones que producen estudiantes de 10 a 12 años cuando resuelven diferentes tareas matemáticas de generalización. En este documento se reporta lo acontecido en la aplicación de secuencias figurales-numéricas y numéricas. Es de particular interés el proceso de generalización y la producción de las expresiones desde la perspectiva teórica de John Mason, quien considera el proceso de generalización como una espiral continua de acciones y que los estudiantes vayan construyendo su propia simbología en lugar de introducir prontamente una notación convencional como acontece en algunas investigaciones (véase por ejemplo Radford, 1999; Schielmann, et al., 2011). Así, los objetivos de investigación son: (1) describir el proceso de generalización de los estudiantes durante la resolución de las tareas de generalización y (2) determinar el alcance de generalización algebraica que manifiestan los estudiantes al expresar la regla de generalización que define a cada tarea matemática. En esta investigación las tareas matemáticas se definen por una regla de generalización que corresponde a la relación entre dos variables.
2. Marco de referencia
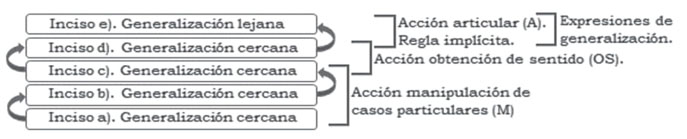
Mason (1996) opina que expresar la generalidad es un proceso que se corresponde con una espiral continua de acciones (ver figura 3) denominadas manipular, obtener sentido de y articular, las cuales se describen a continuación.
La manipulación (sea de objetos físicos, mentales o simbólicos) permite apreciar lo que está sucediendo y detectar patrones, relaciones, generalidades, etc. Resolver uno o varios ejemplos para descubrir lo que está ocurriendo es productivo ya que, los ejemplos son casos particulares de una situación general (Mason et al., 2010). Detectar lo que está sucediendo permite obtener sentido de alguna característica o propiedad de los objetos que se están manipulando, lo que da lugar a articular la estructura que conlleva a la generalización. Cuando esto ocurre, tal expresión se convierte en una entidad que puede ser manipulada y usarse para encontrar otras propiedades, lo que permite continuar de forma ascendente en la espiral empezando un nuevo ciclo de acciones. Mason (1989) sugiere inclusive que el proceso de abstraer en matemáticas ocurre en un cambio momentáneo de articular (fin de un ciclo) a manipular (inicio del siguiente ciclo). Pero, cuando la resolución resulta difícil, y las conjeturas son erróneas, es sensato regresar a manipular nuevos ejemplos para ascender en la espiral.
La obtención de sentido va muy vinculada con articular la generalidad. Para Mason (1989) es importante dar cuenta de la propia generalidad que tratar de traducir la generalidad de alguien más. Existen estudiantes que pueden manipular la generalidad expuesta por el profesor, pero no pueden explicar por qué hacen lo que hacen. La expresión de la generalidad, primero en imágenes o palabras, y luego en expresiones cada vez más concisas utilizando símbolos, es un logro que solo se consigue después de un gran esfuerzo cognitivo.
Adicionalmente, se consideran tres etapas en el proceso de generalización: ver, decir y registrar (Mason et al., 1999). “Ver” se refiere a la identificación mental de una regularidad o relación, esto puede ocurrir después de un periodo de tiempo trabajando con un número de ejemplos particulares, hasta que se logra la identificación de algo común. Ver generalidades implica que los estudiantes puedan identificar factores clave y combinarlos para producir una regla que funcione.
El “decir”, ya sea a uno mismo o a alguien en particular, es articular en palabras aquello que se ha reconocido. Antes de decir las generalidades observadas se suele decir qué ocurre en casos particulares. Mason (1989) concibe que el estudiante puede conversar consigo mismo, esto es, puede ponerse en contacto con cierto contenido, leer un texto y tener un sentido activo (construir, especializarse, conjeturar, generalizar, justificar) guiado por el texto o por materiales diseñados por alguien experto. De cierta manera, el estudiante está conversando con el contenido, mediado por un experto a través de materiales estructurados.
“Registrar” un patrón o relación es hacer visible el lenguaje, lo cual conduce a la simbolización y comunicación escrita. Esta etapa es difícil, tanto para niños como adultos, por lo que no hay que apresurar el uso de los símbolos si aún es prematuro.
2.1. FORMAS DE REGISTRAR
Hay ciertas formas de registro que van desde lo verbal hasta lo completamente simbólico. Para algunas personas solo se reconoce como álgebra la última forma. Sin embargo, de acuerdo con Mason et al. (1999), es importante considerar que el registro de la notación matemática es gradual y los estudiantes necesitan ver que los símbolos se usan para expresar generalidades, y solo los usarán de manera exitosa cuando estén preparados para ello y perciban la necesidad de hacerlo.
A medida que los estudiantes progresan hacia los símbolos hay ciertas etapas que podrían identificarse. En el nivel más simple los registros pueden darse mediante dibujos, o dibujos combinados con palabras, en una etapa posterior puede darse el registro solo con palabras de tal manera que, alguien externo pueda entender lo manifestado. Una siguiente etapa, que posiblemente surge de la necesidad de ser más concisos, es el empleo de la combinación de palabras y símbolos. El uso completo de símbolos suele venir en última instancia. Cabe destacar que no se sugiere que cada estudiante tenga que pasar en orden por dichas etapas.
Desde la perspectiva de este trabajo y de acuerdo con Mason et al. (1999), es importante hacer notar que no solo las expresiones simbólicas son de naturaleza matemática, de hecho, esas expresiones son de gran valor únicamente cuando tienen significado para los estudiantes. Se considera que tanto las formas simbólicas como las verbales representan medios para expresar la generalidad y por lo tanto se consideran algebraicas, aunque se reconoce que para ciertas tareas matemáticas es imprescindible una forma simple y sucinta de registrar. Adicionalmente, se reconoce la importancia de que los estudiantes generen su propia simbología antes de usar la convencional, pero esto requiere de mayor experiencia.
2.2. Estructura matemática
Venkat et al. (2019) destacan la importancia de prestar atención al grado de generalidad en el lenguaje, para explorar aquellas bases que se perciben en una estructura emergente o matemática. Una estructura emergente expresa un enfoque de relación matemática local entre los elementos, donde la apreciación de las propiedades generales aún estaría por emerger. Mientras que, la estructura propiamente matemática tiene un referente más general, con un enfoque
en el que se identifican las propiedades de la relación matemática entre los elementos. La apreciación de la estructura matemática es esencial para la comprensión y está al alcance de los escolares de todas las edades, incluso si no es explícita o no está completamente articulada (Mason et al., 2009).
3. METODOLOGÍA
El estudio es de naturaleza cualitativa y de corte descriptivo (Miles y Huberman, 1994) en virtud de que los datos de interés se analizan, describen e interpretan. También es de tipo longitudinal y de cohorte (Cohen et al., 2007) porque se trabaja con los mismos estudiantes durante dos periodos escolares (2017-2018 y 2018-2019). Se empezó a trabajar con ellos cuando cursaban quinto grado de primaria y lo acontecido durante ese periodo es lo que se reporta en este artículo.
Participaron 25 estudiantes de quinto grado pertenecientes a una escuela pública mexicana. La aplicación se realizó durante el periodo escolar 2017-2018. Cada tarea fue entregada impresa, los estudiantes trabajaron de manera individual y en esta etapa del proyecto no hubo intervención por parte del investigador dando lugar a las producciones primitivas de los estudiantes. Las respuestas se analizan individualmente para identificar el proceso y alcance de la generalización algebraica de las expresiones emitidas por cada estudiante; y se organizan por tarea y por bloque. Los estudiantes se etiquetaron del 1 al 25 por orden alfabético de acuerdo con su primer apellido.
3.1. Diseño de las tareas matemáticas
Se diseñaron 10 secuencias organizadas en dos bloques. El Bloque I se conforma de 8 secuencias figurales-numéricas y el Bloque II de 2 secuencias numéricas.
Bloque I. Cada secuencia es presentada mediante una figura con puntos y el número
de la figura correspondiente. Existen trabajos de investigación (Roig y Llinares, 2008; Warren, 2009) que presentan secuencias
figurales-numéricas usando dos conjuntos de números diferentes (cardinales para
denotar el número de elementos del término y ordinales para denotar la posición
del término). En este trabajo se consideró no involucrar a los números ordinales
y aunque las secuencias poseen un orden, dicho orden se etiquetó con carácter
cardinal. En lugar de escribir 1°, 2°, 3° término, etc., se escribió figura 1, figura 2, figura 3, etc. Así,
la relación entre el número de puntos y número de la figura (estructura
matemática) para cada secuencia, está definida por las siguientes funciones
Se inició este bloque de tareas con la secuencia definida por la función identidad, valorando que los estudiantes podrían identificar y expresar sin dificultad la relación que corresponde al mismo número de puntos y número de figura, además, que este preámbulo pudiera servir de experiencia previa para las diferentes exigencias involucradas en las siguientes tareas. Las secuencias 2 y 3 involucran a los conjuntos de números pares e impares respectivamente, también se valoró que los estudiantes pudieran expresar la regla de generalización correspondiente a cada secuencia, por tener referentes de esos conjuntos de números desde sus primeros años de educación básica.
En la secuencia 4, se pretende que los estudiantes determinen una relación cuadrática. Esta secuencia se incluyó considerando que los estudiantes cuentan con conocimientos previos sobre perímetro y área de rectángulos desde cuarto de primaria (Secretaría de Educación Pública, 2016). Inclusive, el patrón figural presenta intencionalmente puntos distribuidos formando cuadrados para ayudar a encontrar la relación correspondiente. En caso de que los conocimientos previos de área no emergieran en los estudiantes, se opina que podrían establecer la relación mediante el uso adecuado de la multiplicación prestando atención a la organización de los puntos de las figuras.
En las secuencias 5 y 7 se pretende que los estudiantes establezcan una relación
multiplicativa y en las secuencias 6 y 8 una relación aditiva. Están definidas
por
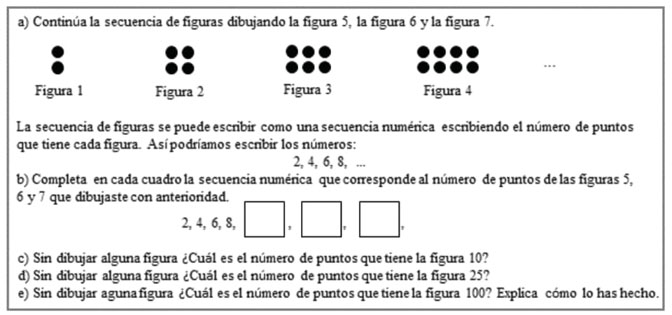
A continuación, se hace referencia a la Secuencia 2 (figura 4) para explicar y referir los elementos generales que conforman a todas las secuencias de este Bloque I, las cuales incluyen cinco incisos:
En el inciso a) se presenta la secuencia por medio de figuras y se solicita continuar la secuencia dibujando las tres figuras siguientes. Se promueve una generalización cercana en virtud de que se puede continuar la secuencia dibujando los siguientes términos hasta llegar al requerido.
En el inciso b) se sustituye la figura por el número de puntos que conforman cada figura con la intención de empezar a guiar al estudiante hacia valores distantes, prescindiendo de dibujar.
En el inciso c) se solicita, sin dibujar figura alguna, el número de puntos de determinada figura no tan alejada de la secuencia numérica. Nuevamente se promueve una generalización cercana, pero en un ámbito numérico. En las secuencias 5 a 8 ya se empieza a solicitar desde este inciso explicar lo realizado para empezar a obtener la expresión de generalización.
En el inciso d) se pide el número de puntos de una figura más distante que la del inciso c). Se considera el valor pedido como generalización cercana. A través de estos cuatro incisos se promueve lo que Mason (1996) denomina manipulación de varios casos concretos que se espera permitirán que los estudiantes vayan apreciando la generalización para poder articularla correctamente. En las secuencias 3 a 8 se solicita explicar lo realizado.
Finalmente, en el inciso e) se promueve una generalización lejana ya que se solicita el número de puntos de una figura que resultaría laborioso o tedioso hallarlo mediante dibujos o por conteo. Se espera que esto lleve al estudiante a la necesidad de buscar una alternativa más eficiente (construcción y explicación de una regla de correspondencia entre las variables involucradas).
Las acciones de la espiral de Mason (1989) se promueven a través de la organización y articulación de las preguntas. Se motiva un razonamiento inductivo (manipulación de casos particulares) con la intención de que los estudiantes identifiquen la relación de correspondencia entre el número de puntos y el número de figura (obtener sentido de) para articular la regla de correspondencia (generalización). Se espera que, en la medida que los estudiantes manipulen los casos particulares “vean” la relación entre las variables de la secuencia (etapa ver del proceso de generalización), identificando aquello que permanece y lo que varía y les permita articular alguna regla de correspondencia. En cada inciso se solicita hacer un registro de tipo figural, numérico o explicativo (etapa registrar), lo cual permitirá apreciar la expresión de generalización que va formulando el estudiante.
Bloque II. En estas secuencias se omite lo figural. Los datos presentados en las secuencias 9 y 10 que conforman este bloque están organizados en un registro tabular (ver figura 5).
La Secuencia 9 corresponde a la relación multiplicativa
En el inciso a) se presentan los primeros siete términos de la secuencia numérica organizados en una tabla horizontal. Se promueve una generalización cercana en virtud de que, mediante conteo se puede encontrar el término requerido.
En el inciso b) ya se solicita formular una expresión que dé cuenta de la generalización.
En el inciso c) se pide explícitamente escribir una regla que permita encontrar cualquier número de la secuencia. Mason et al. (1999) hacen notar la importancia de que los estudiantes expresen las regularidades que perciben ya que esas expresiones serán su álgebra aún incipiente.
En el inciso d) se promueve una generalización lejana. Mediante ese caso particular distante se emprende el regreso en la espiral de acciones para aquellos estudiantes que aún no hayan identificado la regla de generalización.
En el inciso e) se promueve que los estudiantes propongan el número que deseen, ese número peculiar puede ser cercano o distante. Mason (1999) menciona que estas encomiendas tienden, por un lado, a estimular en ellos una conciencia de la gama de elecciones posibles que pueden escoger (valores que corresponden al dominio de la función), y por otro, permiten apreciar cuál es el alcance de la generalidad que para ellos representa la secuencia.
En las dos secuencias de este bloque se fomenta un razonamiento inductivo, pero se destaca la etapa “registrar” durante la resolución. La representación tabular contribuye a una distinción de los dos conjuntos de elementos involucrados y mediante las preguntas se promueve que los estudiantes identifiquen que hay una relación entre ellos.
La espiral de acciones de Mason (1989) se puede percibir en el diseño a través de la manipulación de los casos particulares e interpretación de las tablas que permitan a los estudiantes identificar la relación de correspondencia entre el número y término de la secuencia (obtener sentido de) y así poder articular y expresar la regla de generalización.
3.2. Análisis y resultados
Bloque I. Espiral de acciones. En la figura 6 se presenta la interpretación de la espiral de acciones en relación con las respuestas a los incisos de las secuencias de este bloque.
Las respuestas o procedimientos correctos a los incisos a), b) y c) permiten apreciar en los estudiantes la acción manipular. Además, son indicadores de que empiezan a identificar las regularidades que presentan las secuencias dadas, que van apreciando aquello que permanece y lo que cambia y; junto con la respuesta correcta del inciso d) se interpreta que van obteniendo sentido de la generalización, aunque en algunos casos pueden continuar en la acción manipular. Si adicionalmente se tiene una respuesta correcta en e), se interpreta que los estudiantes han articulado alguna generalidad a través de una regla implícita. Las explicaciones otorgadas en este inciso son las expresiones que permiten identificar la forma del registro y el alcance de la generalidad que ellos manifiestan.
A continuación, se ejemplifica el análisis del proceso de generalización mediante
las respuestas de la Secuencia 1 resuelta por el estudiante 6 (E6). La
estructura matemática que caracteriza a dicha secuencia corresponde a la
relación definida por
A medida que E6 manipula ejemplos con valores cada vez más distantes se interpreta con base en el diagrama de la figura 6, que va transitando de la acción manipular (incisos a, b y c) hacia las acciones obtención de sentido y articular (incisos d y e). Además de articular, E6 expresa la regla de generalización que identifica entre el número de puntos y el número de la figura (figura 8).
Se concluye que E6 transita adecuadamente en las acciones manipular, obtener sentido y articular durante la resolución de la Secuencia 1. Con base en el diagrama de la figura 6 en relación con las acciones y los incisos de la secuencia, las acciones de E6 se sintetizan en Manipular-Manipular-Manipular-Obtención de Sentido-Articular, es decir, M-M-M-OS-A. De manera análoga se realizó el análisis con los 24 estudiantes restantes para la Secuencia 1 y las acciones que se reconocieron se resumen en la tabla 1, identificándose que 23 estudiantes logran completar un ciclo de acciones articulando una regla de generalización que usan de manera implícita para responder correctamente de forma numérica los casos particulares, aunque no todos consiguen expresarla. De modo similar se realizó el análisis por cada estudiante para las otras siete secuencias de este bloque.
Es importante mencionar la distinción entre articular y expresar. Se evidencia en algunos estudiantes el uso de una regla implícita de generalización que les permite resolver correctamente los casos particulares lejanos, es decir, logran articularla, pero no logran expresarla. En otro apartado se explicará respecto a las expresiones de generalización que producen los estudiantes. Para E6 se observa que además de articular una regla de generalización que usa correctamente para resolver los incisos, la expresa en lenguaje natural e inclusive proporciona una expresión simbólica incipiente (inciso e).
Tabla 1 Acciones que se identificaron en los 25 estudiantes en la Secuencia 1 del Bloque I
| E | a) | b) | c) | d) | e) | E | a) | b) | c) | d) | e) | E | a) | b) | c) | d) | e) | ||
| E1 | M | M | M | OS | A | E9 | M | M | M | OS | A | E18 | M | M | M | OS | A | ||
| E2 | M | M | M | OS | E10 | M | M | M | OS | A | E19 | M | M | M | OS | A | |||
| E3 | M | M | M | OS | A | E11 | M | M | M | OS | A | E20 | M | M | M | OS | A | ||
| E4 | M | M | M | OS | E12 | M | M | M | OS | A | E21 | M | M | M | OS | A | |||
| E5 | M | M | M | OS | A | E13 | M | M | M | OS | A | E22 | M | M | M | OS | A | ||
| E6 | M | M | M | OS | A | E14 | M | M | M | OS | A | E23 | M | M | M | OS | A | ||
| E7 | M | M | M | OS | A | E15 | M | M | M | OS | A | E24 | M | M | M | OS | A | ||
| E8 | M | M | M | OS | A | E16 | M | M | M | OS | A | E25 | M | M | M | OS | A | ||
| E17 | M | M | M | OS | A |
Nota: E=Estudiante; M=Acción Manipular; OS=Acción Obtención de Sentido; A=Acción Articular; Espacio en blanco=Se interpreta que el estudiante no logra la acción articular
Bloque II. Espiral de acciones. El diagrama de la figura 9 presenta la interpretación de la espiral de acciones respecto a las respuestas de los incisos de las secuencias de este bloque. Las respuestas o procedimientos correctos de los tres primeros incisos permiten interpretar en los estudiantes la transición de un primer ciclo de acciones: manipular (inciso a), obtener sentido de (inciso b) y articular (inciso c). En c) se solicita explícitamente escribir una regla, pero si los estudiantes no lograran articularla ni expresarla, entonces las respuestas correctas del inciso d) determinarán el tránsito hacia un segundo ciclo de acciones mediante el regreso a la acción manipular de un valor lejano (término 500) que dé lugar a la obtención de sentido y en su caso, a la formulación o reformulación de la regla de generalización. La respuesta correcta al inciso e) es referencia del alcance de la generalización que manifiestan los estudiantes, interpretado a través del valor que proporcionen, según este sea cercano o lejano. Finalmente, las explicaciones otorgadas en los incisos b), c) y la regla solicitada en d) permiten evaluar el registro y las expresiones de generalización.

Elaboración propia
Figura 9 Interpretación de la espiral de acciones en las secuencias del Bloque II.
Para ejemplificar el análisis del proceso de generalización se presenta la
Secuencia 9 contestada por el estudiante 13 (E13), la estructura matemática de
la secuencia corresponde a
En el inciso d), E13 aplica correctamente su regla para el término 500 (figura 11).
De acuerdo con las figuras 8 y 9 se concluye que las acciones de E13 son M-OS-A, primer ciclo de acciones para los incisos a)-c). Seguidamente, M-OS-A para el segundo ciclo de acciones correspondiente al inciso d). Finalmente, en el inciso e) al solicitarle que proporcione el término que desee y encuentre el número correspondiente, E13 escoge el término 600 por lo que, se puede apreciar de acuerdo con Mason (1999) el alcance de la generalidad que representa la secuencia para dicho estudiante. Este valor proporcionado se clasificó como generalización lejana (GL).
De igual modo se realizó el análisis correspondiente de los otros 24 estudiantes para la Secuencia 9 y las acciones que se reconocieron en cada uno se resumen en la tabla 2. Cabe recordar que se promueven dos ciclos de acciones, uno inicial (incisos a, b y c) y uno de regreso (inciso d), así como el alcance de la generalización que percibe cada estudiante (inciso e). Se evidenció que la mayoría de ellos logró transitar entre la acción manipular y obtener sentido desde el primer ciclo de acciones y once lograron articular y usar correctamente una regla de generalización. También se encontró que mediante el inciso d) ocho estudiantes más articularon la regla de generalización para el segundo ciclo de acciones. Respecto al inciso e), a través de los valores proporcionados se puede apreciar el alcance de la generalización que manifestaron algunos estudiantes para dicha secuencia, estos valores se clasificaron como Generalización Cercana Tipo 1 o Tipo 2 (GC1 o GC2) o Generalización Lejana (GL). Finalmente, la Secuencia 10 de este bloque se analizó de manera semejante.
Tabla 2 Resultados de la Secuencia 9 definida por
| E | a), b), c) | d) | e) | E | a), b), c) | d) | e) | |
|---|---|---|---|---|---|---|---|---|
| E1 | M-OS | M-OS-A | GC1 | E14 | M-OS-A | M-OS-A | GC1 | |
| E2 | M-OS-A | M-OS-A | E15 | M | M-OS-A | |||
| E3 | M-OS-A | M-OS-A | GC2 | E16 | M | M-OS-A | GC1 | |
| E4 | NC | E17 | M-OS-A | M-OS-A | GC1 | |||
| E5 | M-OS-A | M-OS-A | GL | E18 | M-OS-A | M-OS-A | GC2 | |
| E6 | M-OS-A | E19 | M-OS | M-OS-A | GC1 | |||
| E7 | M-OS-A | M-OS-A | GL | E20 | M-OS | NC | NC | |
| E8 | M-OS-A | M-OS-A | GC1 | E21 | M-OS-A | M-OS-A | GL | |
| E9 | M-OS | M-OS-A | E22 | M | M-OS-A | |||
| E10 | M-OS | M-OS-A | GL | E23 | M | |||
| E11 | M-OS | E24 | M | NC | ||||
| E12 | M-OS | M-OS-A | GC1 | E25 | M | NC | ||
| E13 | M-OS-A | M-OS-A | GL | |||||
Nota: E=Estudiante; M=Acción Manipular; OS=Acción Obtención de Sentido; A=Acción Articular; GC1=Generalización Cercana Tipo 1 (valores menores que 13); GC2=Generalización Cercana Tipo 2 (valores 30 y 47); GL=Generalización Lejana (valores entre 100 y 1000). Espacio en blanco=Se interpreta que el estudiante no logra alguna de las acciones M, OS, A o no proporciona correctamente un valor en el inciso e). NC=No contestó.
Expresiones de generalización. El segundo análisis que se realizó compete a las expresiones proporcionadas por los 25 estudiantes en cada secuencia para determinar el alcance de generalización algebraica. Las diferentes expresiones encontradas en todas las secuencias se clasificaron en cinco categorías de acuerdo con el alcance de generalización algebraica al expresar la relación de correspondencia que define a cada secuencia. También, fue de interés identificar el tipo de registro proporcionado. Las categorías se describen a continuación y se ejemplifican con respuestas de los estudiantes. Asimismo, para mayor referente se presentan en la tabla 3 la clasificación de todas las respuestas registradas en la Secuencia 1.
Categoría 1. Incluye aquellas expresiones que no refieren a las variables
involucradas, ni a la variación, ni a la relación de correspondencia. Por
ejemplo, en la Secuencia 1 definida por
Categoría 2. Incluye expresiones en las que se mencionan la variación o las variables, pero sin vincularlas a la relación de correspondencia. Por ejemplo, en la Secuencia 1, E16 escribe “70 porque las figuras van de 1 en 1”. En este caso, el estudiante se centra solo en una variable (número de figura) y expresa la variación que percibe entre las figuras, pero no establece una relación de correspondencia. Otro ejemplo lo encontramos en E20 al expresar “70 porque es lo mismo”, en esta expresión, aunque la palabra “mismo” apela a que E20 compara las dos variables involucradas, no escribe la relación de correspondencia de manera explícita.
Categoría 3. Se consideran las expresiones que denotan la relación de
correspondencia para un número particular, es decir, se expresa la
generalización para el número solicitado u otro número al ejemplificar. En la
Secuencia 1, E5 escribe “R=70 ¿Por qué? porque aumenta de 1 en 1 y si es 70 = 70
x 1 = 70” La expresión 70 x 1 = 70 muestra la relación de correspondencia para
el número 70. Dos ejemplos en la Secuencia 2 definida por
Categoría 4. Se consideran aquellas expresiones que dan cuenta, con cierta precisión, de lo que ocurre de manera general con la relación entre las dos variables; por ejemplo, E14 en la Secuencia 1 escribe “70 puntos porque cada punto tiene el mismo número que el de las figuras”. La expresión evidencia la relación de correspondencia con cierta precisión, sin embargo, no cada punto tiene el mismo número que el de las figuras, sino el número de puntos es el mismo número que el de las figuras. También se asume que la expresión proporcionada en esta categoría da referencia a que los estudiantes consideran que la regla se aplica a diferentes valores (sin que se pretenda que ellos tengan noción del conjunto dominio de la relación de correspondencia).
Categoría 5. Las expresiones son más precisas y concisas. Evocan un término cualquiera. Nuevamente se enfatiza que, aunque las expresiones dan cuenta de que los estudiantes consideran una regla que se aplica a diferentes valores, no se asume que ellos tengan noción del conjunto dominio de la relación de correspondencia. Por ejemplo, en la Secuencia 1, E10 escribe “el número de la figura es el mismo que el de los puntos”.
A continuación, en la tabla 3 se presenta la clasificación de todas las respuestas registradas en la Secuencia 1 del Bloque I.
Tabla 3 Expresiones de generalización producidas por los estudiantes en la Secuencia 1, Bloque I
| Categoría 1 | |
| E1: | 70 puntos lo hice contando los números en mi mente y leyendo muy bien las preguntas. |
| E7: | 70 multiplicando y sumando. |
| E12: | 70 pensando cuántos puntos tendría si fuera dibujando. |
| E15: | Con 70 puntos o con otras figuras más. |
| E18: | 70 puntos yo lo he hecho como me lo vaya explicando la pregunta. |
| E19: | Viendo figuras y lo conté y me dio 70. |
| E21: | Tiene 70 me apoyé en el ejemplo. |
| E23: | Sumé de
10 en 10 hasta que llegué a 70, |
| E25: | Primero deberíamos escribir 70 bolitas y ya sabrás el resultado. |
| Categoría 2 | |
| E3: | 70 porque las figuras van de 1 en 1. |
| E9: | Tiene 70 porque es de un puntito por ejemplo si pongo 10 siempre va a ser 10. |
| E11: | 70 porque el número 70 que te muestra es esa cantidad que es. |
| E16: | 70 va aumentando de 1 en 1. |
| E17: | 70 voy siguiendo por los números o por los puntos. |
| E20: | 70 porque es lo mismo. |
| E24: | 70 porque me fijé de los puntos y números. |
| Categoría 3 | |
| E5: | R=70
¿Por qué? porque aumenta de 1 en 1 y si es |
| E13: | 70 puntos. En las figuras se puede ver que avanza de uno en uno así que si la figura 1 tiene un punto la figura 2 tendrá 2 puntos. |
| E22: | 70 puntos yo busque su patrón la figura 1 tiene 1 punto y la figura 2 tiene 2 puntos y así lo estuve haciendo. |
| Categoría 4 | |
| E6: | 70 puntitos cada figura tiene los mismos puntitos. Ejemplo: figura 1 = 1 puntito. |
| E14: | 70 puntos porque cada punto tiene el mismo número que el de las figuras. |
| Categoría 5 | |
| E8: | 70, porque el número de figuras es lo mismo que el de puntos, ejemplo: si el número de figura es 100 igual los puntos serán 100. |
| E10: | 70 puntos el número de la figura es el mismo que el de los puntos. |
4. CONCLUSIONES
Los estudiantes participantes quienes no tienen entrenamiento en tareas de generalización proporcionan, en esta etapa del proyecto de investigación, evidencia de su capacidad de generalizar a partir de casos particulares. La mayoría de ellos puede proporcionar términos lejanos a partir de los términos dados, lo que da cuenta de que reconocen el comportamiento de las variables involucradas. Algunos estudiantes, incluso, expresan de manera concisa la relación de correspondencia que se define en cada tarea matemática. Es importante resaltar las diferencias entre generalizar el patrón de una secuencia (generalizar una variable) y generalizar una regla de correspondencia que involucra establecer una relación entre dos variables.
Los resultados permiten dar cuenta del proceso de generalización en edades tempranas, así como del alcance y registro de la generalización algebraica mediante las expresiones que producen los estudiantes en el marco del modelo de la espiral de acciones propuesto por Mason.
Respecto al proceso de generalización, se encontró que la mayoría de los estudiantes pueden llevar a cabo la acción manipular, hecho que se verifica cuando ellos interpretan los registros tabulares o construyen los términos inmediatos o muy cercanos a partir de los casos particulares proporcionados en cada tarea matemática. Respecto a las acciones obtención de sentido y articular se encontró que algunos estudiantes lograron transitar a dichas acciones. Mason (1989) refiere que la articulación de la generalidad es un logro que se consigue después de un gran esfuerzo cognitivo. Con relación a aquellos estudiantes que no lograron dicho tránsito, en la siguiente etapa de la investigación se incluyen entrevistas semiestructuradas mediante las cuales se pretende identificar y dar cuenta de los obstáculos que dificultan este tránsito.
Respecto a las expresiones de generalización, es importante mencionar que el foco de atención está en identificar el alcance de generalización algebraica que pueden comunicar los estudiantes en forma escrita y sin intervención alguna, siendo de interés las producciones primitivas producidas por los estudiantes. Se reconoce la importancia de este tipo de producciones que permitan promover un siguiente ciclo de acciones o el regreso en la acción manipular en el modelo en espiral propuesto por Mason. El alcance de la generalización algebraica se identifica mediante el registro de la regla de correspondencia entre las dos variables definida en cada tarea matemática, interpretándose que los estudiantes dan cuenta que dicha regla se aplica a diferentes valores (carácter general) sin pretender que ellos tengan noción del conjunto dominio de la regla.
Los resultados proporcionan evidencia de la capacidad que tienen los estudiantes para producir expresiones precisas de generalización algebraica. Las expresiones que se destacan son aquellas clasificadas en las categorías 3, 4 y 5. En la categoría 3, lo que se expresa es una relación matemática local entre números y operaciones, considerándose la presencia de una estructura emergente, debido a que las propiedades generales todavía están por emerger. En la categoría 4, las expresiones no son precisas, pero manifiestan claramente lo que ocurre de manera general con la relación entre las dos variables. En la categoría 5, las expresiones ya comunican de manera concisa y precisa lo que ocurre de manera general con la relación entre las dos variables, es decir, evidencian una generalización de carácter algebraico como se aprecia en la tabla 2 en las respuestas de los estudiantes E8: “porque el número de figuras es lo mismo que el de puntos” y E10: “el número de la figura es el mismo que el de los puntos”, respuestas que corresponden a la Secuencia 2 del Bloque I. De acuerdo con Mason et al. (1999) estas expresiones proporcionan referencia de un álgebra incipiente. Asimismo, las diferentes expresiones dan cuenta de que los registros pueden pasar por diferentes borradores antes de convertirse en concisos y formales.
Se infiere, con base en los resultados, que es factible desarrollar el lenguaje algebraico desde edades tempranas desde una perspectiva en espiral como propone Mason. De acuerdo con Mason et al. (1999), los registros que proporcionan los estudiantes en el proceso de generalización y, por tanto, de la construcción de su lenguaje algebraico suelen ir desde lo verbal hasta lo completamente simbólico. Se considera que el modelo en espiral permitirá explicar esta evolución. Sin embargo, para ello es necesario llevar a cabo estudios longitudinales que permitan dar seguimiento por un tiempo prolongado a un mismo grupo de estudiantes. El proyecto de investigación se encuentra actualmente en una segunda etapa de estudio con los mismos participantes.











 nueva página del texto (beta)
nueva página del texto (beta)