INTRODUCCIÓN
Una de las expectativas de los procesos de enseñanza y de aprendizaje en matemáticas es que los profesores promuevan que los estudiantes sean autónomos en su propio aprendizaje, en términos de que reflexionen y regulen sus acciones en tareas matemáticas.4 Diversos investigadores (Díaz, Pérez, González-Pienda y Núñez, 2017; Preiss, Grau, Torres y Calcagni, 2018) plantean que tal autonomía se puede estimular a través de la implementación de estrategias metacognitivas, pues éstas favorecen que los alumnos se den cuenta de los procedimientos que deben implementar, cómo y para qué llevarlos a cabo ante una tarea matemática. Para Schoenfeld (2012), estas estrategias repercuten en las respuestas que obtienen los estudiantes y pueden incidir en su rendimiento académico.
El estudio de la metacognición surgió desde hace cinco décadas en educación matemática (Desoete y De Craene, 2019) y está centrado, principalmente, en cómo los estudiantes por sí solos regulan sus acciones para dar solución a problemas matemáticos (Díaz, et al., 2017; Schoenfeld, 1992). Algunas de las líneas de investigación en este campo estudian la relación entre creencias, conocimiento matemático y aprendizaje autorregulado (Dignath-van Ewijk y van der Werf, 2012), aprender a aprender matemáticas a través de la metacognición (Iriarte, 2011), y uso de estrategias metacognitivas para el rendimiento académico (Kambita y Hamanenga, 2018).
Actualmente, varios investigadores plantean también la necesidad de poner mayor atención a los factores externos al estudiante que potencializan la metacognición para el aprendizaje autorregulado. Se apunta que la clase de matemáticas es un espacio ideal para fomentar estrategias relacionadas con la metacognición (Mato-Vázquez, Espiñeira y López-Chao, 2017; Rigo, Páez y Gómez, 2010), ya sea de manera deliberada o no (Dignath-van Ewijk y van der Werf, 2012; Mato-Vázquez, et al., 2017). Sin embargo, de acuerdo con la revisión de literatura, se requiere discutir qué estrategias promueve el profesor al enseñar contenidos matemáticos, cómo lo hace y en qué momento de la clase ocurre.
El presente artículo tiene como objetivo plantear una reflexión teórica sobre la forma en que las prácticas docentes potencializan la metacognición en los estudiantes para autorregular su aprendizaje en tareas matemáticas. Para ello, se toma como referente la metáfora de andamiaje (Bruner, 1987), en la cual se concibe que el profesor proporciona los medios o andamios necesarios para solucionar una tarea matemática de manera autónoma y regulada, y a través de este apoyo se potencializan estrategias de corte metacognitivo.
METACOGNICIÓN: INTERACCIÓN ENTRE DOS CONSTRUCTOS
El concepto de metacognición ha sido discutido y usado en diversos contextos de la educación (Desoete y De Craene, 2019; Preiss, et al., 2018) y relacionado, principalmente, con el aprendizaje autorregulado (Martínez, 2017; Schoenfeld, 2012; Zimmerman y Moylan, 2009). A continuación, se recurre a su significado y desarrollo inicial para una mejor comprensión del constructo.
Desde una perspectiva psicológica, en sus primeros estudios, Flavell (1976; Jaramillo y Simbaña, 2014) se dio cuenta de que los niños desarrollaban procesos cognitivos de alto nivel para controlar la memoria y recuperar información. Para el control de memoria identificó que implementaban acciones para almacenar información, por ejemplo, atender, codificar, memorizar y estudiar. Con respecto a la recuperación de información, recurrían a reconocer, recordar y reconstruir, entre otras acciones. Para Flavell (1985) la metacognición se relaciona con la metamemoria, y esta última se refiere a:
los conocimientos y procesos cognitivos que tiene la persona sobre todo lo relativo a la memoria. En la memoria se distinguen, asimismo, entre actividades de almacenamiento y de recuperación. Como sus propios nombres indican, las actividades de almacenamiento sitúan información en la memoria mientras que las actividades de recuperación escogen información de la memoria. Almacenar significa atender, codificar, memorizar, estudiar y cosas por el estilo. Aprender suele ser un buen sinónimo. Recuperar significa reconocer, recordar, reconstruir el recuerdo de lo que se ha almacenado anteriormente. (pp. 277-279)
La metacognición, hoy en día, es definida como el conocimiento que tiene un estudiante de su propia cognición, lo que le permite regular su pensamiento y aprendizaje; consiste en planear, monitorear y evaluar determinados procesos cognitivos que le permitan solucionar tareas específicas de aprendizaje (Martínez, 2017; Medina, Castleberry y Persky, 2017). Las investigaciones más recientes sobre este tema retoman dos tipos de estudios: por un lado, y de acuerdo con Schneider y Artelt (2010), se remiten a los primeros trabajos de Flavell, los cuales aluden al grado de conocimiento y conciencia que posee el alumno de su memoria (Schlagmüller y Schneider 2007, citados en Schneider y Artelt, 2010); y, por otro, discuten la metacognición como un tipo de pensamiento de orden superior que implica un control activo sobre los propios procesos cognitivos involucrados en el aprendizaje de las matemáticas (Baten, Praet y Desoete, 2017).
Dentro de las investigaciones que discuten la metacognición como un tipo de pensamiento de orden superior, se encuentran autores como Osses y Jaramillo (2008), quienes ponen en perspectiva dos constructos teóricos que interactúan entre sí: a) conocimiento cognitivo o metaconocimiento, y b) control metacognitivo o autorregulación del conocimiento. Con el interés de dar cuenta de la relación directa entre ambos constructos, Osses y Jaramillo (2008) señalan lo siguiente:
Se practica la metacognición cuando se tiene conciencia de la mayor dificultad para aprender un tema que otro; [… ] cuando se piensa que es preciso examinar todas y cada una de las alternativas en una elección múltiple antes de decidir cuál es la mejor, cuando se advierte que se debería tomar nota de algo porque puede olvidarse. (p. 191)
De acuerdo con Schoenfeld (1992), el conocimiento cognitivo y metacognitivo se desarrollan simultáneamente en la comprensión de conceptos o procedimientos matemáticos ante una tarea dada; en otras palabras, “los planificadores de problemas efectivos planifican y realizan un seguimiento de qué tan bien van las cosas a medida que implementan sus planes. Si parecen estar progresando, continúan; si hay dificultades, reevalúan y consideran alternativas" (Schoenfeld, 2012, p. 137). A continuación, se describe cada uno de estos constructos.
CONOCIMIENTO COGNITIVO O METACONOCIMIENTO
El metaconocimiento para Flavell (1987, p. 21) es “aquella parte del conocimiento del mundo que uno posee y que tiene que ver con cuestiones cognitivas (o quizá mejor psicológicas)”. Se refiere al componente de tipo declarativo que un alumno tiene acerca de tres tipos de conocimiento: la tarea matemática y sus demandas, los recursos cognitivos disponibles para afrontarla y el procedimiento que puede utilizar para resolver tal tarea (Sáiz y Guijo, 2010).
En relación con el primer conocimiento, la tarea matemática le demanda al estudiante saber cuál es el objetivo que se pretende lograr en ella y qué características tiene, de modo que lo lleve a identificar el nivel de dificultad y a elegir el procedimiento más apropiado para resolverla (Osses y Jaramillo, 2008). Un ejemplo de ello es cuando un alumno en la clase de matemáticas “identifica que la manera en la cual está expuesta el problema dificulta la comprensión” (Klimenko y Alvares, 2009, p. 18) o cuando un estudiante distingue el tipo de tarea y la relación que ésta tiene con sus conocimientos previos (Sáiz y Román, 2011).
El conocimiento sobre los recursos cognitivos incluye las potencialidades y limitaciones cognitivas que el alumno tiene y que le facilitarán desarrollar la tarea matemática, así como tomar consciencia de lo que le afecta para su rendimiento académico (Osses y Jaramillo, 2008). En relación con este conocimiento, se ha reportado que los estudiantes revisan por cuenta propia los procedimientos implementados para resolver problemas matemáticos como una estrategia para validar el resultado (Barrera y Cuevas, 2017; Márquez y Cuevas, 2017).
El tercer tipo de conocimiento implica conocer los procedimientos que el alumno domina para aprender y que puede implementar en la solución de diversas tareas matemáticas (Dignath y Büttner, 2008); por ejemplo, saber que una forma de calcular la pendiente de una gráfica lineal es mediante su definición o a través de dos de sus puntos (Santos, 2010).
CONTROL METACOGNITIVO O AUTORREGULACIÓN DEL CONOCIMIENTO
La autorregulación del conocimiento está relacionada con las estrategias de planear, monitorear y evaluar los procedimientos que usa el estudiante para dar solución a tareas matemáticas. Para Zimmerman y Moylan (2009), estas estrategias se definen como la capacidad que tiene un alumno para utilizar el metaconocimiento de manera eficiente en la solución de tareas, pues le permite darse cuenta de qué conocimientos matemáticos requiere, con cuáles cuenta y cómo implementarlos. En otras palabras, a través del uso de estas estrategias, el alumno es capaz de iniciar, dirigir y regular su propio aprendizaje al realizar una tarea matemática. Desde esta perspectiva, de acuerdo con Barrera y Cuevas (2017), los alumnos llevan a cabo las siguientes acciones para definir el procedimiento de solución ante una tarea dada:
Meditan el plan antes de comenzar a plasmarlo, eligen el método que consideran más pertinente según las necesidades del problema, consideran desde un inicio solo los datos relevantes y decantarse por elegir aquellos tipos de procedimientos que generalmente les funcionan (gráficos, esquemas, dibujos, entre otros). (p. 7)
Después de planear e identificar la alternativa de solución que consideran más viable, los alumnos siguen el plan que han diseñado por lo que desarrollan procedimientos algorítmicos necesarios que incluyen:
La secuencia lógica de sus pasos, ajustes en los cálculos, cambios en su estrategia inicial ya sea porque su método no los llevó a la respuesta [esperada], no les parece que responda a las necesidades del problema o para optimizar la solución. (Barrera y Cuevas, 2017, p. 7)
Una manera de sintetizar lo señalado por Barrera y Cuevas, y que permite visualizar la autorregulación cognitiva de un estudiante al solucionar una tarea matemática, es el Modelo Cognitivo Social de Autorregulación propuesto por Zimmerman y Moylan (2009). Este modelo toma como base aspectos socio-cognitivos, en particular, da cuenta de los factores que influyen para que ocurra la autorregulación del aprendizaje en el contexto de tareas (Panadero y Tapia, 2014).
De acuerdo con el Modelo Cognitivo Social de Autorregulación, la autorregulación del aprendizaje son los “pensamientos, sentimientos y acciones auto-generados para alcanzar los objetivos de aprendizaje” (Zimmerman y Moylan, 2009, p. 299) que el alumno pone en marcha al solucionar una tarea matemática. Además, este Modelo plantea la autorregulación como un proceso cíclico que involucra tres fases o estrategias metacognitivas, las cuales mantienen una estrecha relación entre sí: planear, monitorear y evaluar (figura 1).
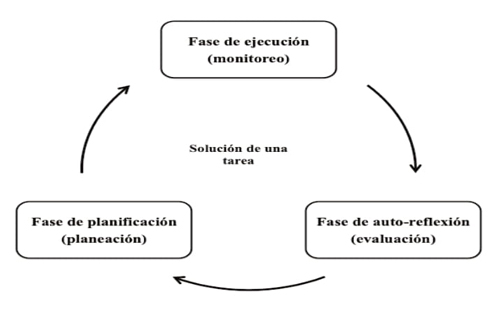
Figura 1 Fases y estrategias metacognitivas para la autorregulación del aprendizaje en la solución de una tarea matemática. Adaptada de Zimmerman y Moylan (2009, p. 300).
En la figura anterior se destacan dos aspectos. El primero tiene que ver con la interrelación entre las estrategias metacognitivas, las cuales dependen de la frecuencia de retroalimentación proveniente de fuentes internas y externas. En el contexto de la educación, la fuente externa se refiere a las acciones del profesor de matemáticas, y la fuente interna a la propia motivación del alumno para llevar a cabo una tarea. Ambas fuentes de retroalimentación son relevantes en el desarrollo e implementación de tales estrategias, la manera en cómo se presentan facilita o debilita el esfuerzo e interés del estudiante para autorregular su aprendizaje.
El segundo aspecto corresponde al concepto de metacognición. En el modelo de Zimmerman y Moylan (2009) la metacognición se concibe como un proceso continuo que involucra la reflexión y la acción. Al ser un “circuito de retroalimentación personal” (p. 300), cuando el alumno realiza una tarea matemática, hace uso de la información sobre su rendimiento y los resultados para implementar futuras adaptaciones.
Con base en lo señalado por Zimmerman y Moylan (2009), en los siguientes apartados se presenta la descripción de cada estrategia metacognitiva y la relación entre ellas al momento de solucionar una tarea matemática.
PLANEACIÓN: ¿QUÉ TENGO QUE HACER PARA DAR RESPUESTA A LA TAREA MATEMÁTICA?
Para afrontar una tarea matemática, se espera que el estudiante trace un plan de acción, es decir, que determine el procedimiento o el algoritmo de solución (Polya, 1979; Schoenfeld, 1992). La planeación, como estrategia metacognitiva, surge cuando el alumno se enfrenta a una tarea e involucra la motivación, los procesos cognitivos y su esfuerzo para resolver la tarea, de modo que lo lleven a establecer el procedimiento a utilizar (Zimmerman y Moylan, 2009).
La planeación implica que el alumno analice la tarea a partir de sus conocimientos previos, es decir, que la descomponga en indicaciones o identifique los datos clave para determinar cómo resolverla (Polya, 1979; Santos, 2010). También permite que el alumno diseñe una estrategia personal en la que establezca objetivos para resolver la tarea matemática, de acuerdo con sus características particulares, las habilidades y el tiempo que disponga (Zimmerman, 2008).
El análisis de la tarea involucra dos elementos: establecer metas y elaborar un plan de acción, donde el alumno elige las estrategias de tipo cognitivas y relacionadas con el manejo de recursos didácticos y matemáticos (Quintana-Terés, 2014). Además de analizar la tarea, el alumno identifica creencias de tipo motivacional que repercuten en sus acciones en relación con el cumplimiento de la tarea. Las creencias, de acuerdo con Zimmerman (2008), pueden estar relacionadas con: autoeficacia, expectativas de resultados, interés, valor intrínseco de la tarea matemática, así como orientación hacia el cumplimiento de ésta como meta de aprendizaje. Enseguida, se explican con mayor detalle.
La autoeficacia le permite al estudiante motivarse y darse cuenta de la capacidad que tiene para cumplir con un determinado nivel de desempeño en la tarea. Por otra parte, las expectativas de resultados se refieren a las creencias que tiene un alumno sobre la posibilidad de éxito que tendrá al realizar determinada tarea matemática. Además, el interés y valor intrínseco de la tarea representan el grado de importancia que el alumno le asigna y reflejan el compromiso que tiene para realizarla y culminarla.
Otras creencias motivacionales que Zimmerman y Moylan (2009) identifican son las referidas a la orientación hacia la meta, que es el compromiso que un alumno tiene con el logro de las metas establecidas en la planeación. Tener metas le permite al estudiante considerarse capaz de lograr la tarea, dedicar mayor tiempo y esfuerzo para tal logro. En este contexto, el alumno trata de demostrar su capacidad para recibir opiniones favorables sobre su desempeño, tomando como base su esfuerzo (Quintana-Terés, 2014).
Una manera de potencializar la estrategia de planificación en la clase de matemáticas es impulsar a los alumnos a que se cuestionen a sí mismos sobre su entendimiento de la tarea antes de iniciar el proceso de solución. Lo anterior puede promoverlo un docente a través de plantear preguntas que lleven a los alumnos a pensar si comprendieron la instrucción, si identificaron los datos necesarios en la tarea matemática (Fourés, 2011) y los procedimientos que consideran necesarios para resolver la tarea matemática. En este sentido, Polya (1979) señala:
cuando el profesor hace a sus alumnos una pregunta o una sugerencia [… ], puede proponerse dos fines. Primero, el ayudar al alumno a resolver el problema en cuestión. Segundo, el desarrollar la habilidad del alumno de tal modo que pueda resolver por sí mismo problemas ulteriores. (p. 27)
MONITOREO: ¿LO ESTOY HACIENDO BIEN?
La estrategia de monitoreo permite que el estudiante controle sus acciones y procesos cognitivos, por ejemplo, procedimientos matemáticos o algoritmos que realiza para resolver una tarea matemática. Según el modelo de Zimmerman y Moylan (2009), esta estrategia está en la fase de ejecución. El monitoreo involucra el autocontrol y la auto-observación; a continuación, se explica cada uno.
El autocontrol se refiere a mantener la concentración y el interés en la solución de una tarea, lo cual incluye poner en marcha una serie de estrategias de monitoreo específicas y generales. Las estrategias de tipo específicas puntualizan el desarrollo de un proceso sistemático para atender aspectos propios de una tarea, por ejemplo: subrayar un texto para recordar las ideas o conceptos matemáticos más importantes (Panadero y Tapia, 2014). Por su parte, las estrategias de tipo general están relacionadas con la motivación y le permiten al alumno incentivar y mantener el interés para realizar la tarea. Una de estas estrategias ocurre cuando el estudiante se habla a sí mismo para recordar el objetivo por cumplir y así regula su motivación, por ejemplo: “este problema no va a poder conmigo, conseguiré averiguar cómo resolverlo” (Panadero y Tapia, 2014, p. 456).
La auto-observación hace referencia al seguimiento de tipo mental que el alumno realiza en función de: a) los resultados de su desempeño y de la calidad de lo que hizo, b) los procedimientos para dar solución a una tarea matemática, y c) su eficacia para lograr los objetivos previamente planteados. Así, en caso de que un estudiante realice de manera incorrecta la tarea y se dé cuenta de ello, la auto-observación le permitirá revisar sus procedimientos matemáticos y volver a implementarlos o determinar uno nuevo, esto último requerirá que regrese a la fase de planeación. Cabe señalar que, para Panadero y Tapia (2014), la auto-observación se logra si el alumno realiza auto-monitoreo, auto-registro de las acciones y procedimientos implementados en la tarea matemática.
El auto-monitoreo es comparado con la auto-evaluación durante la realización de una tarea y se refiere a comparar lo que se está realizando en función de algún criterio que sirva como base para valorar la ejecución. El auto-registro, por su parte, consiste en anotar las acciones que se realizan durante la ejecución de una tarea matemática (Panadero y Tapia, 2014), por ejemplo, cuando un alumno apunta, mentalmente o por escrito, la cantidad de tiempo que le lleva resolver una ecuación de segundo grado, con la finalidad de resolver otras ecuaciones en un menor tiempo.
Ahora bien, en la clase de matemáticas, el docente al fungir como mediador puede plantearle preguntas que lleven a los alumnos a verificar, rectificar y revisar el procedimiento que ha determinado para dar solución a una tarea dada. Tomando en consideración la idea de Polya (1979), en torno a las fases de resolución de problemas, el maestro puede preguntarle, por ejemplo, si ha seguido el plan que había diseñado previamente o por qué el procedimiento implementado funciona para una tarea o si funcionará para tareas similares.
EVALUACIÓN: ¿LO HE HECHO BIEN?
La evaluación como estrategia de aprendizaje metacognitiva está relacionada con la respuesta y el producto final de una tarea matemática, e implica que el alumno reconozca qué tanto la planeación y el monitoreo influyeron en los resultados que obtuvo. De acuerdo con Zimmerman y Moylan (2009), la evaluación tiene dos componentes: el auto-juicio y la auto-reacción.
El auto-juicio tiene que ver con la reflexión que el alumno hace en términos de juzgar su actuación en la solución de la tarea: si el procedimiento lo implementó de manera adecuada o si le faltó hacer algo. Para Panadero y Tapia (2014), la autoevaluación y atribuciones causales son los componentes del auto-juicio. En la auto-evaluación, el alumno compara su desempeño con la meta inicial, el desempeño y las respuestas de sus compañeros o la respuesta dada por el docente (Quintana-Terés, 2014). Las atribuciones causales implican que el estudiante considere las creencias con relación a las causas de los resultados, “negativo -contrario a lo esperado- o positivo”, que obtuvo al concluir la tarea (Panadero y Tapia, 2014, p. 458).5 Estas creencias responden tanto a factores internos como externos; dentro de los internos se encuentran el esfuerzo, suerte o grado de habilidad, y en los externos, están el nivel de demanda cognitiva de la tarea y la exigencia del docente para realizarla (Quintana-Terés, 2014).
La auto-reacción está vinculada con el comportamiento de los alumnos en respuesta a los juicios propios sobre los procedimientos realizados para el cumplimiento de la tarea. La auto-reacción comprende la satisfacción y las decisiones de tipo adaptativas y defensivas. De acuerdo con Quintana-Terés (2014), las decisiones adaptativas ocurren cuando el estudiante tiene la disposición para seguir usando o modificar un determinado procedimiento o algoritmo matemático, y las decisiones defensivas hacen que el alumno evite realizar esfuerzos adicionales para aprender, esto con el interés de prevenir futuras insatisfacciones.
Para potencializar la evaluación, como estrategia metacognitiva, el docente de matemáticas, puede hacer preguntas que guíen a los alumnos hacia la reflexión y revisión con respecto al procedimiento utilizado para resolver la tarea, por ejemplo, que identifiquen si éste fue ejecutado de manera correcta y si se verificó el resultado obtenido (Ellis, Denton y Bond, 2014). El docente le puede solicitar al alumno que argumente la razón de utilizar determinado procedimiento, o que describa cómo lo seleccionó e implementó, así como la percepción sobre su rendimiento en la solución de la tarea (Klimenko y Alvares, 2009).
PRÁCTICA DOCENTE Y METACOGNICIÓN EN MATEMÁTICAS
En educación matemática existe una variedad de estudios teóricos y empíricos que abordan el tema de la metacognición debido a su relevancia en la enseñanza y aprendizaje de las matemáticas (Kambita y Hamanenga, 2018). Por ejemplo, la investigación desarrollada por Díaz, et al. (2017) tuvo como objetivo dar cuenta de la forma en que varios docentes promueven que sus estudiantes universitarios realicen las siguientes actividades al resolver una tarea matemática:
1) efectuar una reflexión sobre formas de estudio para alcanzar un determinado objetivo [… ]; 2) comentar brevemente [… ] experiencias personales sobre procedimientos de planificación del estudio, formas de estudio que facilitan la comprensión y la supervisión del propio proceso de estudio; 3) posteriormente a la clase, estudiar en forma autónoma el tema. (p. 97)
Los resultados presentados por Díaz, et al. (2017) muestran que cuando los alumnos reciben orientación y apoyo por parte del docente, tienen mayores puntuaciones en autorregulación del aprendizaje, así como un aumento en la percepción sobre la eficacia de las estrategias de aprendizaje metacognitivas. En este estudio, Díaz, et al. emplearon un diseno cuasi-experimental, donde participaron tres docentes que estaban a cargo de tres materias, en tres carreras universitarias seleccionadas por la semejanza en sus objetivos y contenidos de estudio.
Otra de las líneas de investigación es la evaluación de estrategias metacognitivas en la resolución de problemas matemáticos. Diversos estudios resaltan que el nivel metacognitivo de los estudiantes es eficiente y, que utilizan con mayor frecuencia estrategias de monitoreo, mientras que la planificación y evaluación las emplean en menor medida (Barrera y Cuevas, 2017; Fernández y García, 2013). En el estudio realizado por Barrera y Cuevas (2017) se aplicó un test con cinco problemas de aritmética y una entrevista semiestructurada sobre los propios procesos de resolución de problemas a 14 estudiantes universitarios, de 18 a 25 años de edad. Los resultados muestran un escaso uso de estrategias metacognitivas por parte de los estudiantes al resolver los problemas y presentan dificultades para reflexionar sobre sus procedimientos de solución.
Una tercera línea, que ha emergido en las últimas dos décadas, versa sobre el papel del profesor en el desarrollo de la metacognición para el aprendizaje autorregulado en la solución de tareas matemáticas. Al respecto, diversas investigaciones postulan que las estrategias metacognitivas pueden ser enseñadas de manera intencionada o imprevista (Dignath-van Ewijk y van der Werf, 2012) teniendo diferentes niveles de impacto en los aprendizajes de los estudiantes. Rigo, et al. (2010) señalan que la enseñanza de las estrategias metacognitivas puede darse cuando el docente les solicita a los alumnos que argumenten o demuestren si el procedimiento matemático que usaron ante una determinada tarea es correcto o si funciona para tareas similares, lo anterior como un medio para la generalización del procedimiento. En este sentido, durante la enseñanza de las matemáticas, el profesor brinda oportunidades para que el estudiante cuestione, monitoree y evalúe su aprendizaje.
Entre otras líneas de investigación se pueden mencionar los estudios que centran su atención en la relación entre conocimiento y las creencias de los docentes sobre el fomento de la autorregulación para el logro de aprendizaje, por ejemplo, Dignath-van Ewijk y van der Werf (2012) encontraron que algunos docentes “disponen de actitudes positivas hacia la idea de proporcionar autonomía en el estudiante” (p. 8), pero otros desconocen cómo apoyar la autorre-gulación de manera efectiva en los alumnos para así lograr una autonomía en su aprendizaje. Lo anterior refleja la necesidad de conocer qué es lo que los docentes conocen y creen con respecto a la metacognición y a potencializarla en sus alumnos.
ANDAMIAJE: UN MEDIO PARA PROMOVER ESTRATEGIAS METACOGNITIVAS
La interacción social entre el docente y los alumnos es fundamental para el aprendizaje de las matemáticas, así como el uso de estrategias metacognitivas y el desarrollo de tareas (Larios, Font, Giménez y Díaz, 2012). Esta interacción puede darse a través de lo que Bruner (1987; van de Pol, Volman y Beishuizen, 2010) llama andamiaje, donde el aprendizaje se da como un proceso colaborativo y de manera autorregulada. Según el Modelo Cognitivo Social de Autorregulación (Zimmerman y Moylan, 2009), las estrategias metacognitivas pueden ser promovidas y potencializadas en el alumno a partir de intervenciones que hace el docente en la solución de tareas matemáticas.
Desde la perspectiva sociocultural, el aprendizaje ocurre con apoyo de otros (Vygotsky, 1978), como lo es el docente. Al tener mayor dominio sobre un tema, se espera que el profesor proporcione los medios necesarios para desarrollar habilidades en el alumno que le permitan solucionar la tarea matemática de manera autónoma y regulada (Bruner, 1987; Wood, Bruner y Ross, 1976). Para Bruner (1987) tal apoyo debe ser provisional, de modo que en un sentido metafórico sea un andamiaje que vincule los conocimientos previos del alumno y los que se espera construya al realizar una tarea por sí solo.
El andamiaje en la enseñanza de las matemáticas implica un “… control adulto [i.e., del profesor] de aquellos elementos de la tarea que inicialmente están más allá de la capacidad del aprendiz, lo que permite concentrarse y completar solo aquellos elementos que están dentro de su rango de competencia” (Wood, et al., 1976, p. 90). En este sentido, el docente tiene el objetivo de mediar el logro de los aprendizajes de manera paulatina, hasta que la responsabilidad de manejar y dominar el proceso de aprendizaje y logro de la tarea matemática sea solo del alumno.
Para que ocurra el andamiaje en matemáticas, el profesor debe implementar las siguientes acciones: a) motivar al estudiante durante el desarrollo de una tarea matemática; b) mantener el interés en el alumno por resolver la tarea, c) acompañar al alumno en el manejo y control de la frustración tras intentar una actividad y no lograrla (Bruner, 1987; Wood, et al., 1976). Además, tales acciones, como objetivo del andamiaje, deben lograr que sea el alumno quien determine, implemente y argumente el procedimiento de solución (Medina, et al., 2017).
Diversas investigaciones en educación matemática (van de Pol, et al., 2010; van de Pol, Volman, Oort y Beishuizen, 2015) distinguen tres elementos específicos del andamiaje: a) contingencia, b) desvanecimiento y c) transferencia de responsabilidad. Enseguida se describe en qué consiste cada uno de ellos.
El primero se refiere a que el apoyo brindado por el docente debe estar al mismo nivel o que se pueda adaptar al grado actual del rendimiento del alumno o de lo que el docente pueda percibir como competencia que ya es capaz de desarrollar el estudiante, por él mismo. Es importante que en este elemento del andamiaje, el docente de matemáticas adecue su nivel de comprensión con el del alumno, de tal manera que le brinde el profesor las condiciones para que construya sobre lo que conoce, y el maestro pueda decidir sobre cuándo retirar el apoyo, en función de las respuestas del alumno (van de Pol, et al., 2010). Por ejemplo, Schoenfeld (2012) plantea que antes de resolver un problema, el estudiante asimila y se orienta a la situación y hacia cierta información que ya conoce.
El desvanecimiento del apoyo, pasando del andamiaje más directivo e intenso en la etapa inicial, a formas más autorreguladas, dependerá del nivel del desarrollo y competencia del alumno. Cuando se está aprendiendo una actividad nueva o el desarrollo de una tarea matemática, el andamiaje es oportuno, ya que a través de ayudas verbales, físicas o estímulos cognoscitivos se va instruyendo sobre cómo y qué hacer. A medida que el alumno va interiorizando esos procedimientos, llega un punto en que ya no le son necesarios (van de Pol, et al., 2010).
Por último, la transferencia de responsabilidad se dirige hacia una entrega gradual del desempeño de una tarea matemática al estudiante (van de Pol, et al., 2010). En este elemento, el docente debe considerar y enfocar su atención en las respuestas de los alumnos, en brindar tiempo suficiente para que recuperen información, desarrollen sus respuestas, y para impulsar en ellos la posibilidad de realizar tareas por sí solos.
Como parte de algunos datos empíricos que reflejan cómo el andamiaje influye en la enseñanza y en el aprendizaje de matemáticas, se retoman las ideas presentadas por Márquez y Cuevas (2017); quienes resaltan que, al enseñar contenidos matemáticos, el profesor modela procedimientos que le permiten al alumno con apoyo y, en un momento dado, de manera autónoma planear, monitorear y evaluar su aprendizaje, al grado de que generaliza los conocimientos matemáticos (e.g., fórmulas, conceptos y procedimientos).
Lo anterior muestra que, desde la perspectiva del andamiaje, los docentes de matemáticas deben orientar las tareas hacia la reflexión, autocontrol y direccionalidad del aprendizaje, de modo que provoquen en el estudiante la necesidad de usar estrategias cognitivas y metacognitivas (Klimenko y Alvares, 2009).
CONSIDERACIONES FINALES
La revisión de literatura presentada evidencia la necesidad de estudios centrados en la práctica del profesor y de los estudiantes en la clase de matemáticas, como sus contribuciones discursivas que den cuenta de las interacciones que propician el aprendizaje en matemáticas (van de Pol, et al., 2010). Con esta idea, se retoma el interés de este artículo, que analiza cómo el andamiaje propuesto por el docente en su práctica promueve la reflexión y potencializa la metacognición en el alumno para el aprendizaje autorregulado en tareas matemáticas, ya que de acuerdo con Jiménez y Gutiérrez (2017), lo que el docente de matemáticas piense o conciba determina su estilo y forma de enseñanza, y esto se refleja en su práctica docente.
Las diversas líneas de investigación aquí expuestas, destacan el uso de estrategias metacognitivas en la solución de tareas matemática para lograr un aprendizaje autónomo, que le permita al alumno autorregularse al realizar otras tareas matemáticas. Dichas líneas también sugieren la necesidad de documentar de qué manera y en qué situaciones se promueve y mejora el aprendizaje metacognitivo en los estudiantes de matemáticas, en contextos no intervenidos y en diferentes niveles educativos (Educación Básica, Media Superior y Superior), pues en todos los grados o niveles, el docente tiene la responsabilidad de promover y generar espacios donde el alumno autorregule su aprendizaje (NCTM, 2014).
La literatura muestra que, en la clase de matemáticas se puede promover de manera deliberada o no el uso de estrategias metacognitivas. A la luz de esto, se sugieren futuras líneas de investigación desde un enfoque cualitativo que permitan describir a profundidad la realidad de la práctica docente en educación matemática. Resulta importante realizar estudios que centren el interés en conocer la relación entre las creencias y el conocimiento de los docentes acerca de sus propias estrategias metacognitivas y estudiar si predicen la promoción de la autorregulación cognitiva en sus alumnos durante la clase y a través del andamiaje (Dignath-van Ewijk y van der Werf, 2012).
El análisis propuesto da pie para presentar posibles investigaciones que den cuenta de la efectividad del andamiaje en la clase de matemáticas y en los niveles de educación Media Superior y Superior, pues el alumno de estos niveles sigue en proceso de formación en conocimientos, habilidades y desarrollo de estrategias de aprendizaje que le permitan aprender a lo largo de la vida. Además, es necesario documentar cómo se promueve la metacognición a través del andamiaje al plantear tareas matemáticas en la clase. Por último, resulta trascendental analizar y describir la práctica docente para fomentar la mejora en sus propios procesos metacognitivos y la reflexión profesional de su quehacer (Grau, Calcagni, Preiss y Ortiz, 2017), ya que los docentes al ser expertos en el contenido matemático poseen una completa comprensión de los contenidos que enseñan, por lo que son capaces de presentar los temas utilizando diversas estrategias (Preiss, et al., 2018).











 nueva página del texto (beta)
nueva página del texto (beta)



