Ecuaciones para estimar biomasa total de candelilla (Euphorbia antisyphilitica Zucc.) en Chihuahua

Maldonado-Ortiz, Margarito; López-Serrano, Pablito Marcelo; Valdez-Cepeda, Ricardo D.; Mata-González, Ricardo; García-González, Fabián; Martínez-Salvador, Martín; Maldonado-Ortiz, Margarito; López-Serrano, Pablito Marcelo; Valdez-Cepeda, Ricardo D.; Mata-González, Ricardo; García-González, Fabián; Martínez-Salvador, Martín

doi:10.29298/rmcf.v13i72.1231

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de ciencias forestales

versión impresa ISSN 2007-1132

Rev. mex. de cienc. forestales vol.13 no.72 México jul./ago. 2022 Epub 22-Ago-2022

https://doi.org/10.29298/rmcf.v13i72.1231

Artículo científico

Ecuaciones para estimar biomasa total de candelilla (Euphorbia antisyphilitica Zucc.) en Chihuahua

Margarito Maldonado-Ortiz¹

Pablito Marcelo López-Serrano²
http://orcid.org/0000-0003-0640-0606

Ricardo D. Valdez-Cepeda¹
http://orcid.org/0000-0002-6990-3502

Ricardo Mata-González³
http://orcid.org/0000-0003-2053-7027

Fabián García-González¹

Martín Martínez-Salvador⁴^*
http://orcid.org/0000-0002-2679-5070

^¹Unidad Regional Universitaria de Zonas Áridas, Universidad Autónoma Chapingo. México.

^²Falcultad de Ciencias Forestales, Universidad Juárez del Estado de Durango. México.

^³Department of Animal and Rangeland Sciences, Oregon State University. USA.

^⁴Facultad de Zootecnia y Ecología, Universidad Autónoma de Chihuahua. México.

Resumen

La candelilla (Euphorbia antisyphilitica) es un arbusto que crece en las zonas áridas del norte de México. Esta especie se cosecha para extraer una cera que produce como respuesta al estrés hídrico. Para autorizar la recolección de las plantas, es necesario realizar estimaciones indirectas mediante ecuaciones predictivas de su biomasa. El objetivo del presente estudio fue generar ecuaciones alométricas para estimar biomasa de candelilla a partir de variables morfométricas. El trabajo se llevó a cabo en la región de Aldama y Coyame del Sotol en el noreste de Chihuahua, México. Se aplicó un muestro selectivo y destructivo de 198 individuos de candelilla, los cuales se obtuvieron en ejidos con programas de manejo forestal vigente. Para ajustar la mejor ecuación se probaron cuatro modelos y diferentes combinaciones de variables predictoras de biomasa. Las variables se transformaron a escala logarítmica. Se seleccionó el modelo de Schumacher y Hall en la forma logarítmica con el uso del diámetro de copa y diámetro de la base de la planta, ya que fue el que presentó los mejores ajustes estadísticos (R ² _adj =0.83), la raíz del cuadrado medio del error (RCME=0.042), y los parámetros del modelo fueron significativos (p<0.0001) en su corrección de los supuestos de regresión. La ecuación obtenida es confiable para estimar biomasa de candelilla en el noreste del estado de Chihuahua, México.

Palabras clave Biomasa de arbustos; cera de candelilla; ecuaciones alométricas; modelos; predicción de biomasa; zonas áridas

Abstract

Candelilla (Euphorbia antisyphilitica Zucc.) is a shrub that grows in the arid zones of northern Mexico. This species is harvested for the purpose of extracting a wax that it produces in response to water stress. In order to authorize the harvesting of plants, it is necessary to estimate their biomass indirectly through predictive equations. The objective of this study was to generate allometric equations to estimate the biomass of candelilla based on morphometric variables. The work was carried out in the region of Aldama and Coyame del Sotol in northeastern Chihuahua, Mexico. A selective and destructive sampling of 198 individuals of candelilla was applied, which were obtained in ejidos with forest management programs in force. Four models and different combinations of biomass predictor variables were tested to fit the best equation. Variables were transformed to logarithmic scale. The Schumacher and Hall model was selected in the logarithmic form determined by the crown diameter and base diameter of the plant, since it exhibited the best statistical adjustments (R ² _adj =0.83), as well as by the root mean square of the error (RMSE=0.042), and the model parameters were significant (p<0.0001) in their correction of the regression assumptions. The equation thus obtained is reliable for estimating the biomass of candelilla in the northeastern state of Chihuahua, Mexico.

Key words Shrub biomass; Candelilla wax; allometric equations; models; biomass prediction; arid zones

Introducción

La candelilla (Euphorbia antisyphilitica Zucc.) se reproduce por rizomas, y forma grupos de tallos en manchones de plantas que crecen en el semidesierto del norte de México (^{Arato et
al., 2014}). Esta especie produce una cera natural como un mecanismo para tolerar el déficit hídrico, la cual se cosecha para su comercialización en los mercados nacional e internacional (^{Rojas et al., 2011}; ^{Muñoz-Ruiz et al., 2016}).

En México, la recolección de la candelilla la realizan, principalmente, habitantes de núcleos poblacionales de las zonas áridas de los estados de San Luis Potosí, Zacatecas, Coahuila y Chihuahua (^{Villa-Castorena
et al., 2010}; ^{Becerra-López et al., 2020}). Los procedimientos de extracción, la estimación de la biomasa, las intensidades de recolecta y la regeneración del taxón, han sido objeto de estudio con fines de conservación y manejo, ya que se ocasionan alteraciones en su distribución y abundancia por efecto tanto del aprovechamiento inadecuado, como por influencia del cambio climático (^{Vargas-Piedra et al.,
2020}).

La generación de ecuaciones alométricas para estimar biomasa o volúmenes, es un tema ampliamente estudiado para las especies arbóreas de bosques templados y tropicales, no solo de México, sino a nivel internacional (^{Vargas-Larreta et al., 2017}; ^{Martínez-Domínguez et al., 2020}; ^{Martínez-Sánchez et al.,
2020}). Sin embargo, en taxones arbustivos y plantas de las zonas semiáridas, la generación de estas ecuaciones es poco estudiada, aún para las especies que se aprovechan con fines comerciales (^{Flores-Hernández
et al., 2020}; ^{Villavicencio-Gutierrez et al., 2020}). Además, es necesario desarrollarlas a nivel de regiones ecológicas debido a la amplia variación de condiciones ambientales en las que crecen los taxa del semidesierto, tal es el caso de la candelilla (^{Hernández-Ramos et
al., 2019}; ^{Luo et
al., 2020}; ^{Vargas-Piedra
et al., 2020}).

Entre los trabajos publicados en relación con ecuaciones para estimar biomasa de candelilla, destacan los producidos para algunas regiones en el estado de Coahuila (^{Flores del Angel, 2013}), las cuales fueron generadas a partir de datos de altura media de la planta y diámetros de copa. Recientemente, ^{Hernández-Ramos et
al. (2019)} documentan ecuaciones para algunos municipios del estado de Coahuila con ajustes aceptables en los estimadores estadísticos, ello permite confiabilidad para la estimación de biomasa de la especie en estas regiones; sin embargo, para Chihuahua no hay ecuaciones con validez científica.

El objetivo del presente estudio fue generar ecuaciones alométricas para estimar biomasa total utilizando variables morfométricas de Euphorbia antisyphylitica, para la región de Aldama y Coyame del Sotol en el noreste de Chihuahua, México.

Materiales y Métodos

Ubicación y descripción del área de estudio

La investigación se desarrolló en los municipios Coyame del Sotol y Aldama del estado de Chihuahua, México (Figura 1). La vegetación arbustiva predominante está compuesta por matorral desértico micrófilo y rosetófilo con dominancia de Euphorbia antysiphilitica, Agave lechuguilla Torr., Larrea tridentata (DC.) Coville y Dasylirion sp. Zucc. (^{Granados-Sánchez
et al., 2011}). Las cotas altimétricas del área oscilan de 940 a 1 500 m, con precipitaciones medias anuales de 200 a 400 mm y temperatura media anual de 24 °C (Granados-Sánchez et al., 2011; ^{González-Medrano, 2012}).

Figura 1 Localización del área de estudio en los municipios Aldama y Coyame del Sotol del estado de Chihuahua, México.

Levantamiento de datos

Los datos se colectaron en ejidos y comunidades que tienen estudios técnicos vigentes para el aprovechamiento de la candelilla (Cuadro 1). Para este trabajo, se consideró el término “planta” a la colonia compacta de candelillas que crecen en manchones independientes, y se consideraron al menos 20 centímetros de separación entre las bases de las colonias. Los individuos se seleccionaron de acuerdo con sus características de salud y tamaño, y se evitaron plantas enfermas o poco densas. Las muestras se obtuvieron considerando la variabilidad de condiciones de crecimiento que existen en las poblaciones de las plantas. Se realizó un procedimiento de medición destructivo de 198 plantas distribuidas en siete ejidos con permisos de aprovechamiento forestal para candelilla. A cada ejemplar se le midieron las variables morfométricas: altura total media (Atm), altura promedio de los extremos de la copa del arbusto sin considerar la altura central de la planta, la cual es comúnmente mayor; altura total (At), altura total de la planta que incluye el tallo más largo de la porción central de la copa; diámetro de la base (Db), diámetro de la base de la planta medido 10 cm sobre la superficie del suelo; y diámetro de copa (Dc), promedio del diámetro menor y mayor de la amplitud de copa medidos en forma perpendicular en dirección norte-sur y este-oeste. Posteriormente, cada planta fue extraída para obtener el peso de biomasa total verde (kg) incluyendo la raíz (^{Villavicencio-Gutiérrez et al.,
2018}).

Cuadro 1 Distribución de muestras de las poblaciones de Euphorbia antisyphilitica Zucc. en el área de estudio.

Municipio	Predios	Muestras
Aldama	Chorreras	92
Coyame del Sotol	Cañón de Barrera	58
	El Táscate	19
	Francisco Portillo	6
	San Pedro	23
Total		198

Base de datos

En gabinete, se estimaron las variables diámetro medio de copa (Dc) y la cobertura copa (Ca), la cual se obtuvo utilizando la fórmula del área de un círculo con el diámetro medio de copa.

Resumen descriptivo de las variables

En el Cuadro 2, se observa que en las plantas de candelilla se registró un intervalo de biomasa de 0.09 a 12.89 kg por planta. También se observa el amplio intervalo en el tamaño de las plantas muestreadas, lo cual permite utilizar la ecuación resultante para la mayoría de los tamaños posibles de planta presentes en campo.

Cuadro 2 Resumen estadístico de Euphorbia antisyphilitica Zucc. en los municipios Coyame del Sotol y Aldama, estado de Chihuahua.

Variable	n	Mínimo	Máximo	Media	DE	CV (%)
Db (cm)	198	7	91.00	29.20	18.41	63.05
At (cm)	198	17	105.00	46.43	15.33	33.02
Atm (cm)	198	10	80.00	30.00	11.05	36.83
Dc (cm)	198	14.5	147.50	50.53	25.88	51.22
Da (m²)	198	0.02	1.71	0.25	0.27	108.00
Biomasa (kg)	198	0.09	12.89	1.85	2.33	125.95

Db = Diámetro base; At = Altura total; Atm = Altura media; Dc = Diámetro copa; Da = Cobertura de copa; n = Tamaño de muestra; DE = Desviación estándar; CV = Coeficiente de variación.

Selección de variables predictoras

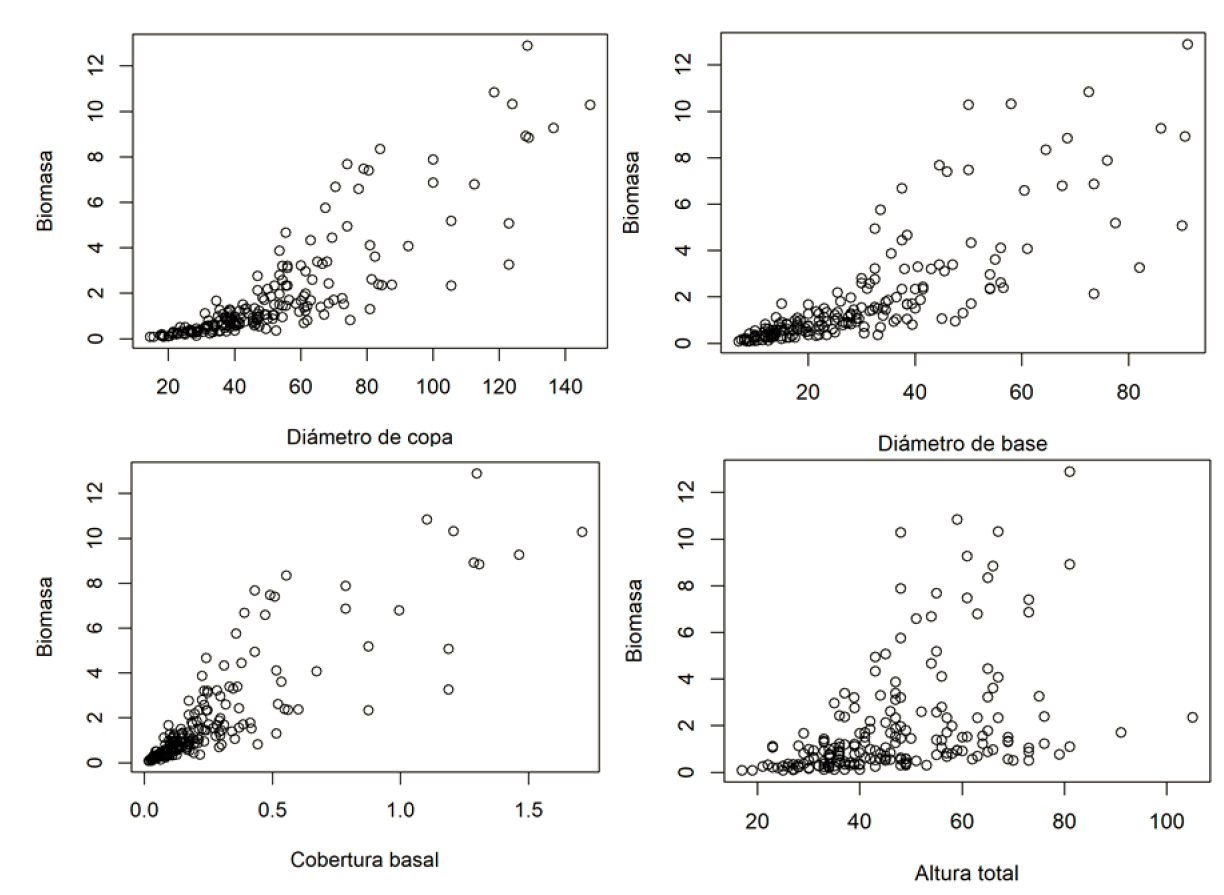
Se realizó la prueba de correlación de Pearson que incluyó a todas las variables para identificar su relación con la biomasa de las plantas. Esto con la finalidad de identificar las variables correlacionadas con la biomasa e identificar las variables predictoras. Se utilizaron gráficas de distribución para visualizar la relación entre la variable dependiente (biomasa) y las independientes (diámetro de copa, diámetro de base, cobertura copa y altura) (Figuras 2 y 3).

Figura 2 Prueba de correlación de variables morfométricas y biomasa de candelilla.

Figura 3 Relación de la biomasa con las variables predictores de Euphorbia antisyphilitica Zucc.

Selección de modelos

Para determinar la biomasa de E. antisyphilitica, se seleccionaron ecuaciones con criterios de flexibilidad con diferentes combinaciones de variables (Cuadro 3). Estas ecuaciones han tenido buenas predicciones de biomasa en varias especies forestales (^{Návar, 2010}; ^{Noulèkoun et al., 2018}; ^{Altanzagas et al.,
2019}). En los estudios alométricos de biomasa, las varianzas del error para las ecuaciones no lineales basadas en unidades aritméticas, no son constantes (heterocedasticidad) para todas las observaciones (^{Chave et al., 2005}). Para eliminar ese problema, el uso de las transformaciones logarítmicas es uno de los métodos más usados para disminuir la influencia de los errores (^{Moussa y Mahamene, 2018}; ^{Zhao et al., 2018}). En consecuencia, se utilizaron las ecuaciones logarítmicas para estimar la biomasa de la candelilla (Cuadro 3). Las ecuaciones alométricas en su forma logarítmica, los predichos conducen a un sesgo sistemático; para minimizarlo, se calculó el factor de corrección (FC) en cada modelo (^{Sprugel, 1983}).

Cuadro 3 Ecuaciones logarítmicas propuestas para determinar la biomasa de Euphorbia antisyphilitica Zucc.

Ec.	Ecuación logarítmica	Ecuación original	Tipo
1.1	ln(B)=ln⁡(B0)+(B1) ln(Dc)	B=β0DcB1	Alométrico
1.2	ln(B)=ln⁡(B0)+(B1) ln(Ca)	B=β0CaB1	Alométrico
1.3	ln(B)=ln⁡(B0)+(B1) ln(Db)	B=β0DbB1	Alométrico
2.1	ln(B)=ln⁡(B0)+B1 ln(Db)+B2 ln(At)	B=β0DbB1 AtB2	Schumacher y Hall
2.2	ln(B)=ln⁡(B0)+B1 ln(Dc)+B2 ln(Db)	B=β0DcB1 DbB2	Schumacher y Hall
2.3	ln(B)=ln⁡(B0)+B1 ln(Db)+B2 ln(Atm)	B=β0DbB1 AtmB2	Schumacher y Hall
3.1	ln(B)=ln⁡(B0)+(B1) ln(Dc2*At)	B=β0(Dc2*At)B1	Spurr
3.2	ln(B)=ln⁡(B0)+(B1) ln(Dc2*Db)	B=β0(Dc2*Db)B1	Spurr
3.3	ln(B)=ln⁡(B0)+(B1) ln(Db2*Dc)	B=β0(Db2*Dc)B1	Spurr
4.1	ln(B)=ln⁡(B0)+(B1) ln(At*Ca)	B=β0(At*Ca)B1	Spurr
4.2	ln(B)=ln⁡(B0)+(B1) ln(Dc*Db)	B=β0(Dc*Db)β1	Spurr

Fuente: ^{Návar, 2010}; ^{Noulèkoun et al.,
2018}; ^{Altanzagas
et al., 2019}.

Ec = Ecuación; B = Biomasa; B ₀ , B ₁ y B ₂ = Parámetros de los modelos; ln = Logaritmo natural.

FC=exp⁡SEE22

Donde:

FC = Factor de corrección

SEE = Error estándar de la estimación

exp = Función exponencial

Análisis estadístico

Los modelos se ajustaron por el método de Mínimos Cuadrados Ordinarios (MCO) (^{Montgomery et al.,
2021}). La selección del modelo se basó en criterios de ajuste de las ecuaciones, específicamente en la significancia de los parámetros (p≤0.05). Además, en la evaluación de las ecuaciones se consideraron el coeficiente de determinación ajustado (R ² _adj ), la raíz del error medio cuadrático (REMC), el criterio de información de Akaike (AIC), el criterio de información Bayesiano (BIC) y el porcentaje medio absoluto del error (PMAE) (^{Picard et al., 2015}; ^{Islam et al., 2021}). Posteriormente, para validar las ecuaciones se verificaron los supuestos de las regresiones de acuerdo con sus predicciones, la normalidad se verificó con la prueba de Lilierfors, mientras que el cumplimiento de homocedasticidad se evaluó con la prueba de Breusch-Pagan (^{Villavicencio-Gutiérrez et
al., 2018}; ^{Flores-Hernández et al., 2020}; ^{Villavicencio-Gutierrez et al.,
2020}). La corrección de la autocorrelación se realizó con el método cochrane.orcutt (^{Kutner
et al., 2005}) con la librería orcutt de R Project, la cual contempla un modelo autorregresivo en tiempo continuo (^{Quiñonez-Barraza et al., 2018}). Finalmente, para detectar multicolinealidad se utilizó el factor inflación de varianza (VIF) (^{Mahmood et
al., 2019}). Todos los análisis estadísticos y gráficos se realizaron con las funciones lm y plot en el software R Project (^{R Core
Team, 2021}).

Resultados

Estadísticos básicos de las variables morfométricas

El resultado del análisis de correlación de Pearson muestra que las variables que registraron mayor correlación con la biomasa fueron la cobertura de copa (r=0.86), el diámetro de copa (r=0.85) y el diámetro de la base (r=0.80) (Figura 2). Sin embargo, en el análisis de regresión lineal se utilizaron todas las variables seleccionadas para obtener los mejores ajustes.

Ecuaciones de biomasa

Los parámetros estimados fueron significativamente diferentes de cero a un nivel de significancia de 5 % (p<0.0001). Los estadísticos de ajuste (R ² _adj , REMC, IAC y BIC) presentaron valores parecidos en las diferentes ecuaciones (Cuadro 4). De acuerdo con los criterios de selección, las ecuaciones 2.2 y 3.2 fueron seleccionadas para estimar la biomasa, ya que ambas tuvieron el R ² _adj más altos (0.84), y en la REMC, el AIC y el BIC registraron los valores más bajos. Se verificaron los supuestos de regresión; por su parte, la prueba de Lillierfos evidenció normalidad de los residuos: D=0.047, valor p=0.345 y D=0.039, valor p=0.0641, para las ecuaciones 2.2 y 3.2, respectivamente (Cuadro 5). La prueba de Breusch Pagan mostró una ligera presencia de heterocedasticidad: BP=9.180, valor p=0.050 y PB=8.697, valor p=0.003, para las ecuaciones 2.2 y 3.2, respectivamente. La prueba de Durbin-Watson fue de 1.34 para las dos ecuaciones, lo que indica que existió una cierta consideración de autocorrelación entre las variables. Ante estas evidencias, se corrigieron las ecuaciones para obtener estimaciones confiables en la predicción de biomasa de la candelilla (Cuadro 5).

Cuadro 4 Valores de parámetros estimados y sus estadísticos de bondad de ajuste de las ecuaciones logarítmicas para predecir biomasa en Euphorbia antisyphilitica Zucc.

Ecuación	Parámetro	Estimador	Error Estándar	Valor t	Valor p	Variable	R ² _adj	REMC	AIC	BIC	FC
1.1	B1	-8.12	0.27	-30.05	0.0001	Dc	0.82	0.47	268.38	278.25	1.12
	B2	2.13	0.07	30.29	0.0001
1.2	B1	1.96	0.07	26.91	0.0001	Ca	0.82	0.47	268.38	278.25	1.12
	B2	1.06	0.03	30.29	0.0001
1.3	B1	-5.19	0.20	-25.01	0.0001	Db	0.77	0.54	323.30	333.17	1.16
	B2	1.62	0.06	25.45	0.0001
2.1	B1	-7.04	0.41	-16.803	0.0001	Db, At	0.79	0.51	301.59	314.74	1.14
	B2	1.45	0.06	20.752	0.0001
	B3	0.63	0.12	4.981	0.0001
2.2*	B1	-7.46	0.28	-25.741	0.0001	Dc, Db	0.84	0.45	247.66	260.81	1.10
	B2	1.46	0.15	9.676	0.0001
	B3	0.58	0.12	4.87	0.0001
2.3	B1	-6.66	0.35	-18.643	0.0001	Db, Atm	0.79	0.51	302.22	315.37	1.14
	B2	1.42	0.07	19.427	0.0001
	B3	0.62	0.12	4.911	0.0001
3.1	B1	-9.58	0.35	-27.32	0.0001	Dc ² *At	0.79	0.51	299.75	309.61	1.14
	B2	0.84	0.03	27.47	0.0001
3.2*	B1	-7.32	0.22	-32.39	0.0001	Dc ² *Db	0.84	0.45	246.28	256.15	1.10
	B2	0.677	0.02	32.39	0.0001
3.3	B1	-6.26	0.21	-29.21	0.0001	Db ² *Dc	0.82	0.48	275.91	285.78	1.12
	B2	0.614	0.02	29.60	0.0001
4.1	B1	-1.63	0.06	-23.45	0.0001	At*Ca	0.79	0.51	299.75	309.61	1.14
	B2	0.84	0.03	27.4	0.0001
4.2	B1	-6.80	0.21	-31.04	0.0001	Dc*Db	0.83	0.46	256.67	266.53	1.11
	B2	0.97	0.03	31.39	0.0001

R ² _adj = Coeficiente de determinación ajustado; REMC = Raíz del error medio cuadrático; AIC = Criterio de información de Akaike; BIC = Criterio de información Bayesiano; FC = Factor de corrección; Db = Diámetro base; Dc = Diámetro copa; At = Altura total; Atm = Altura media; Ca = Cobertura copa; * = Modelo seleccionado.

Cuadro 5 Supuestos de normalidad, heterocedasticidad y valor inflación de las ecuaciones ensayadas.

Ecuación	Lilierfors	Valor p	Breusch Pagan	Valor p	Durbin Watson	VIF
1.1	0.042	0.521	9.227	0.002	1.350
1.2	0.042	0.521	9.227	0.002	1.357
1.3	0.039	0.632	1.102	0.293	1.299
2.1	0.042	0.507	3.181	0.203	1.193	1.342
2.2	0.047	0.345	9.180	0.050	1.346	5.186
2.3	0.031	0.900	1.728	0.410	1.260	1.469
3.1	0.040	0.581	5.910	0.015	1.028
3.2	0.039	0.641	8.697	0.003	1.340
3.3	0.030	0.910	4.027	0.044	1.308
4.1	0.040	0.580	5.910	0.015	1.028
4.2	0.042	0.510	6.448	0.011	1.322

La corrección se realizó con la prueba de Cochrane Orcutt. Al corregir la autocorrelación, se presentaron estimaciones confiables para predecir la biomasa (Cuadro 6). La prueba de Durbin-Watson aumentó 2.19 para las dos ecuaciones seleccionadas. La prueba de Breusch Pagan indicó la ausencia de heterocedasticidad: BP=3.689, valor p=0.15 y BP=3.286, valor p=0.47, Ecuación 2.2 y 3.2, respectivamente.

Cuadro 6 Estimaciones obtenidas en la corrección de autocorrelación y heterocedasticidad de la ecuación 2.2 y 3.2.

Ecuación	Parámetro	Estimador	Error estándar	Valor t	Valor p	R ² _adj	REMC	FC
2.2	B1	-7.03	0.27	-25.157	0.0001	0.83	0.42	1.09
	B2	1.36	0.14	9.484	0.0001
	B3	0.57	0.11	4.897	0.0001
3.2	B1	-6.93	0.23	-30.134	0.0001	0.83	0.42	1.09
	B2	0.64	0.02	30.814	0.0001

R ² _adj = Coeficiente de determinación ajustado; REMC = Raíz del error medio cuadrático; FC = Factor de corrección.

La capacidad predictiva del modelo 2.2 mostró un porcentaje medio absoluto del error de 3.6 %, mientras que la ecuación 3.2, fue de 3.8 %. Por lo tanto, los criterios analizados favorecen a la Ecuación 2.2 para estimar la biomasa verde de candelilla. Las estimaciones obtenidas son alternativas para predecir la biomasa de candelilla mediante el uso de la transformación inversa a una escala logarítmica, por lo que se sugiere utilizar la siguiente ecuación para la estimación de biomasa de candelilla en la región de estudio:

B=exp⁡-7.03+1.36*lnDc+0.57*lnDb* 1.15 Ec. 2.2

Donde:

B = Biomasa (kg)

ln = Logaritmo natural

exp = Función exponencial

Dc = Diámetro de copa (cm)

Db = Diámetro de base (cm)

Discusión

Las variables independientes de las plantas de candelilla mostraron una buena correlación con la biomasa, principalmente la cobertura de copa, el diámetro de copa y el diámetro de la base. La altura total y la altura media presentaron una relación más débil. Al respecto, destaca que a diferencia de la mayoría de las especies arbóreas cuya predicción de biomasa y volumen se realiza con datos de altura y diámetro de los individuos, en los taxones arbustivos si existen otras variables predictoras que dependen de las formas de la planta.

Por ejemplo, ^{Pando-Moreno et al.
(2004)} probaron varias variables para predecir la biomasa de lechuguilla (Agave lechuguilla Torr.) y determinaron que el volumen del cogollo, como variable independiente, registró mayor coeficiente de correlación contra la biomasa del cogollo. Por su parte, ^{Villavicencio-Gutierrez et al. (2018)} identificaron una relación confiable entre el diámetro promedio de copa y el diámetro de base con la biomasa de Lippia graveolens Kunth en las zonas áridas mediante la ecuación de Schumacher y Hall. Sobresale que en las especies arbustivas con formas irregulares, es más necesario realizar un análisis de variables para obtener las que mejor predicen la biomasa y evitar multicolinealidad (^{Daryanto et al.,
2013}; ^{Dai et al.,
2020}).

En este estudio, las ecuaciones alométricas en las que se utilizaron las variables diámetro de copa y diámetro de la base, permitieron estimar la biomasa de candelilla con mayor precisión. Estas ecuaciones tuvieron un REMC (0.42) bajo y una R ² _adj (0.82) estadísticamente aceptable (p<0.0001). Al respecto, algunos estudios indican que el diámetro de copa es una variable confiable para estimar la biomasa de los arbustos en zonas áridas y semiáridas (^{Ali et al., 2015}; ^{Sione et al., 2019}; ^{Aranha et al., 2020}; ^{Chieppa et al., 2020}).

La predicción de biomasa o volúmenes en especies de porte arbustivo, suele presentar valores aceptables. Sin embargo, los estadísticos de prueba comúnmente presentan valores más bajos en comparación con la predicción de biomasa en taxones arbóreos, especialmente en coníferas, las cuales por lo general mantienen formas cónicas y sólidas, a diferencia de los arbustos, los cuales son muy ramificados y poco uniformes (^{Pando-Moreno et al.,
2004}; ^{Zhang et al.,
2016}; ^{Vargas-Larreta et
al., 2017}; ^{Yao et
al., 2021}). En este sentido, el presente estudio no fue la excepción, ya que los máximos valores en el coeficiente de determinación (R ² _adj ) fueron de 0.84 en comparación con ecuaciones de modelos para especies arbóreas, cuyos coeficientes son generalmente superiores a 0.90 (^{Vargas-Larreta et al.,
2017}).

En el caso de candelilla que se documenta, el modelo de Schumacher y Hall (Ecuación 2.2) en su forma logarítmica, predijo la biomasa de la candelilla con coeficientes estadísticamente aceptables. Las formas generales de esas ecuaciones se han utilizado en otras investigaciones en ambientes áridos y semiáridos (^{Návar et al., 2004}; ^{Flores-Hernández et al.,
2020}), por lo que se ratifica su efectividad. Además, es importante destacar que los diámetros de copa y de la base de los arbustos son fáciles de medir en la candelilla, la cual crece en colonias o grupos pequeños de tallos formando manchones amplios desde la base (^{Flores-del Angel et
al., 2013}; ^{Bañuelos-Revilla
et al., 2019}). Finalmente, las estimaciones obtenidas pueden utilizarse para calcular la biomasa área de E. antisyphilitica para las zonas áridas del estado de Chihuahua.

Conclusión

La ecuación alométrica de Schumacher y Hall en su forma logarítmica, puede usarse para estimar la biomasa de Euphorbia antysiphilitica en la región noreste de Chihuahua. La ecuación seleccionada incluye variables morfométricas de fácil medición como la variable de copa y el diámetro de base de las plantas.

Los modelos ensayados en este estudio se recomiendan para estimar la biomasa verde de candelilla, la cual se requiere en los estudios técnicos y programas de manejo de la especie en los municipios de Aldama y Coyame del Sotol en el noreste de Chihuahua, México.

Agradecimientos

Los autores agradecen al fondo sectorial Conacyt-Conafor por el financiamiento del proyecto “Mejores prácticas y generación de tablas de volumen y biomasa para las principales especies forestales no maderables y de importancia económica en los ecosistemas áridos y semiáridos de México”.

Referencias

Ali, A., M. S. Xu, Y. T. Zhao, Q. Q. Zhang, L. L. Zhou, X. D. Yang and E. R Yan. 2015. Allometric biomass equations for shrub and small tree species in subtropical China. Silva Fennica 49(4):1-10. Doi: 10.14214/sf.1275. [ Links ]

Altanzagas B., Y. Luo, B. Altansukh, C. Dorjsuren, J. Fang and H. Hu. 2019. Allometric Equations for estimating the above-ground biomass of five forest tree species in Khangai, Mongolia. Forests 10(8):661. Doi: 10.3390/f10080661. [ Links ]

Aranha, J., T. Enes, A. Calvão and H. Viana. 2020. Shrub biomass estimates in former burnt areas using Sentinel 2 images processing and classification. Forests 11(5):555. Doi: 10.3390/f11050555. [ Links ]

Arato, M., S. Speelman and G. Van Huylenbroeck. 2014. The contribution of non-timber forest products towards sustainable rural development: The case of Candelilla wax from the Chihuahuan Desert in Mexico. Natural Resources Forum 38(2):141-153. Doi: 10.1111/1477-8947.12043. [ Links ]

Bañuelos-Revilla, J. E., J. Palacio-Núñez, J. F. Martínez-Montoya, G. Olmos-Oropeza y J. A. Flores-Cano. 2019. Distribución potencial y abundancia de candelilla (Euphorbia antisyphilitica) en el norte de Zacatecas, México. Madera y Bosques 25(1):1-14. Doi: 10.21829/myb.2019.2511657. [ Links ]

Becerra-López, J. L., R. Rosales-Serna, M. Ehsan, J. S. Becerra-López, A. Czaja, J. L. Estrada-Rodríguez, U. Romero-Méndez, S. Santana-Espinoza, C. M. Reyes-Rodríguez, J. C. Ríos-Saucedo and P. A. Domínguez-Martínez. 2020. Climatic change and habitat availability for three sotol species in Mexico: A vision towards their sustainable use. Sustainability 12(8):3455. Doi: 10.3390/su12083455. [ Links ]

Chave, J., C. Andalo, S. Brown, M. A. Cairns, … and T. Yamakura. 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145(1):87-99. Doi: 10.1007/s00442-005-0100-x. [ Links ]

Chieppa, J., S. A. Power, D. T. Tissue and U. N. Nielsen. 2020. Allometric estimates of aboveground biomass using cover and height are improved by increasing specificity of plant functional groups in Eastern Australian Rangelands. Rangeland Ecology and Management 73(3):375-383. Doi: 10.1016/j.rama.2020.01.009. [ Links ]

Dai, J., H. Liu, Y. Wang, Q. Guo, … and Z. Jiang. 2020. Drought-modulated allometric patterns of trees in semi-arid forests. Communications Biology 3(1):1-8. Doi: 10.1038/s42003-020-01144-4. [ Links ]

Daryanto, S., D. J. Eldridge and H. L. Throop. 2013. Managing semi-arid woodlands for carbon storage: Grazing and shrub effects on above and belowground carbon. Agriculture, Ecosystems & Environment 169:1-11. Doi: 10.1016/j.agee.2013.02.001. [ Links ]

Flores del Angel, M. L. 2013. Situación actual de las poblaciones de Candelilla (Euphorbia antisyphilitica Zucc): Inventario, su propagación sexual y asexual en el estado de Coahuila, México. Tesis Doctoral. Facultad de Ciencias Biológicas, Universidad Autónoma de Nuevo León. San Nicolás de las Garzas, NL, México. 134 p. [ Links ]

Flores-del Angel, M. L., R. Foroughbakhch, A. Rocha-Estrada, M. L. Cárdenas-Ávila, M. A. Guzmán-Lucio, Y. L. Hernández-Aguilar and M. A. Alvarado-Vázquez. 2013. Morphology, viability and germination of candelilla seeds (Euphorbia antisyphilitica Zucc.). Phyton 82:161-167. Doi: 10.32604/phyton.2013.82.161. [ Links ]

Flores-Hernández, C. de J., J. Méndez-Gonzalez, F. de J. Sánchez-Pérez, F. M. Méndez-Encina, Ó. M. López-Díaz and P. M. López-Serrano. 2020. Allometric equations for predicting Agave lechuguilla Torr. aboveground biomass in Mexico. Forests 11(7):784. Doi: 10.3390/f11070784. [ Links ]

González, M. F. 2012. Las zonas áridas y semiáridas de México y su vegetación. Secretaría de Medio Ambiente y Recursos Naturales (Semarnat) e Instituto Nacional de Ecología (INE). Tlalpan, México D. F., Mexico. 173 p. [ Links ]

Granados-Sánchez, D., A. Sánchez-González, R. L. Granados V. y A. Borja de la R. 2011. Ecología de la vegetación del desierto chihuahuense. Revista Chapingo Serie Ciencias Forestales y del Ambiente 17(Edición especial):111-130. Doi: 10.5154/r.rchscfa.2010.10.102. [ Links ]

Hernández-Ramos, A., A. Cano-Pineda, C. Flores-López, J. Hernández-Ramos, X. García-Cuevas, M. Martínez-Salvador y L. Martínez Á. 2019. Modelos para estimar biomasa de Euphorbia antisyphilitica Zucc. en seis municipios de Coahuila. Madera y Bosques 25(2):1-13. Doi: 10.21829/myb.2019.2521806. [ Links ]

Islam, R., S. Azad, A. S. Mollick, M. Kamruzzaman and N. I. Khan. 2021. Allometric equations for estimating stem biomass of Artocarpus chaplasha Roxb. in Sylhet hill forest of Bangladesh. Trees, Forests and People 4:100084. Doi: 10.1016/j.tfp.2021.100084. [ Links ]

Kutner, M. H., C. J. Nachtsheim, J. Neter and W. Li. 2005. Applied linear statistical models. McGraw-Hill Irwin. New York, NY, USA. 1396 p. [ Links ]

Luo, Y., X. Wang, Z. Ouyang, F. Lu, L. Feng and J. Tao. 2020. A review of biomass equations for China’s tree species. Earth System Science Data 12(1):21-40. Doi: 10.5194/essd-12-21-2020. [ Links ]

Mahmood, H., M. R. H. Siddique, L. Costello, L. Birigazzi, … and F. K. Mondol. 2019. Allometric models for estimating biomass, carbon and nutrient stock in the sal zone of Bangladesh. iForest Biogeosciences and Forestry 12(1):69-75. Doi: 10.3832/ifor2758-011. [ Links ]

Martínez-Domínguez, A., F. Ruiz-Aquino, W. Santiago-García, P. Antúnez, M. Á. López-López, C. Valenzuela-Encinas and R. Feria-Reyes. 2020. Allometric equations to estimate aboveground and belowground biomass of Pinus patula Schiede ex Schltdl. & Cham. Forest Science and Technology 16(3):161-170. Doi: 10.1080/21580103.2020.1801526. [ Links ]

Martínez-Sánchez, J. L., C. Martínez-Garza, L. Cámara and O. Castillo. 2020. Species-specific or generic allometric equations: which option is better when estimating the biomass of Mexican tropical humid forests? Carbon Management 11(3):241-249. Doi: 10.1080/17583004.2020.1738823. [ Links ]

Montgomery, D. C., E. A. Peck and G. G. Vining. 2021. Introducction to linear regression analysis. Jhon Wilwey & Sons, Inc. Hoboken, NJ, USA. 704 p. [ Links ]

Moussa, M. and L. Mahamane. 2018. Allometric models for estimating aboveground biomass and carbon in Faidherbia albida and Prosopis africana under agroforestry parklands in drylands of Niger. Journal of Forestry Research 29(6):1703-1717. Doi: 10.1007/s11676-018-0603-z. [ Links ]

Muñoz-Ruíz, C. V., S. López-Dáz, F. Covarrubias-Villa, E. Villar-Luna, J. R. Medina-Medrano and L. G. Barriada-Bernal. 2016. Effect of abiotic stress conditions on the wax production in candelilla (Euphorbia antisyphilitica Zucc.). Revista Latinoamerica de Química 44(1):26-33. https://www.researchgate.net/publication/311705358 . (1 de octubre de 2021). [ Links ]

Návar, J. 2010. Measurement and assessment methods of forest aboveground biomass: A Literature review and the challenges ahead. In Momba M., N. B. (Ed.) Biomass. Sciyo. Rijeka, Croatia. pp. 27-64. https://www.intechopen.com/chapters/11396 . (1 de octubre de 2021). [ Links ]

Návar, J., E. Méndez, A. Nájera, J. Graciano, V. Dale and B. Parresol. 2004. Biomass equations for shrub species of Tamaulipan thornscrub of North-eastern Mexico. Journal of Arid Environments 59(4):657-674. Doi: 10.1016/j.jaridenv.2004.02.010. [ Links ]

Noulèkoun, F., J. B. Naab, J. P. A. Lamers, S. Baumert and A. Khamzina. 2018. Sapling biomass allometry and carbon content in five afforestation species on marginal farmland in semi-arid Benin. New Forests 49(3):363-382. Doi: 10.1007/s11056-017-9624-2. [ Links ]

Pando-Moreno, M., O. Eufracio, E. Jurado and E. Estrada. 2004. Post-harvest growth of lechuguilla (Agave lechuguilla Torr., Agavaceae) in northeastern Mexico. Economic Botany 58(1):78-82. Doi: 10.1663/0013-0001(2004)058[0078:PGOLAL]2.0.CO;2. [ Links ]

Picard, N., E. Rutishauser, P. Ploton, A. Ngomanda and M. Henry. 2015. Should tree biomass allometry be restricted to power models? Forest Ecology and Management 353:156-163. Doi: 10.1016/j.foreco.2015.05.035. [ Links ]

Quiñonez-Barraza, G., G. G. García-Espinoza y O. A. Aguirre-Calderón. 2018. ¿Cómo corregir la heterocedasticidad y autocorrelación de residuales en modelos de ahusamiento y crecimiento en altura? Revista Mexicana de Ciencias Forestales 9(49):28-59. Doi: 10.29298/rmcf.v9i49.151. [ Links ]

R core Team. 2021. The R Project for Statistical Computing. Vienna, Austria. R Foundation for statistical computing. https://www.r-project.org/ . (1 de diciembre de 2021). [ Links ]

Rojas M., R., S. Saucedo P., M. A. De León Z., D. Jasso C. y C. N. Aguilar. 2011. Pasado, presente y futuro de la candelilla. Revista Mexicana de Ciencias Forestales 2(6):7-18. Doi: 10.29298/rmcf.v2i6.571. [ Links ]

Sione, S. M. J., H. J. Andrade-Castañeda, S. G. Ledesma, L. J. Rosenberger, J. D. Oszust and M. G. Wilson. 2019. Aerial biomass allometric models for Prosopis affinis Spreng. in native espinal forests of Argentina. Revista Brasileira de Engenharia Agrícola e Ambiental 23(6):467-473. Doi: 10.1590/1807-1929/agriambi.v23n6p467-473. [ Links ]

Sprugel, D. G. (1983). Correcting for bias in log-transformed allometric equations. Ecology 64: 209-210. Doi: 10.2307/1937343. [ Links ]

Vargas-Larreta B., C. A. López-Sánchez, J. J. Corral-Rivas, J. O. López-Martínez, C. G. Aguirre-Calderón and J. G. Álvarez-González. 2017. Allometric equations for estimating biomass and carbon stocks in the temperate forests of North-Western México. Forest 8(8):269. Doi: 10.3390/f8080269. [ Links ]

Vargas-Piedra, G., R. D. Valdez-Cepeda, A. López-Santos, A. Flores-Hernández, N. S. Hernández-Quiroz and M. Martínez-Salvador. 2020. Current and future potential distribution of the xerophytic shrub candelilla (Euphorbia antisyphilitica) under two climate change scenarios. Forests 11(5):530. Doi: 10.3390/f11050530. [ Links ]

Villa-Castorena, M., E. A. Catalán-Valencia, M. A. Inzunza-Ibarr, M. de L. González-López y J. G. Arreola-Ávila. 2010. Producción de plántulas de candelilla (Euphorbia antisiphyllitica Zucc.) mediante estacas. Revista Chapingo Serie Ciencias Forestales y del Ambiente 16(1):37-47. Doi: 10.5154/r.rchscfa.2009.07.027. [ Links ]

Villavicencio-Gutierrez, E. E., A. Hernández-Ramos, C. N. Aguilar-González y X. García-Cuevas. 2018. Estimación de la biomasa foliar seca de Lippia graveolens Kunth del sureste de Coahuila. Revista Mexicana de Ciencias Forestales 9(45):187-205. Doi: 10.29298/rmcf.v9i45.139. [ Links ]

Villavicencio-Gutierrez, E. E., S. Mendoza-Morales y J. Méndez G. 2020. Modelo para predecir biomasa foliar seca de Litsea parvifolia (Hemsl.) Mez. Revista Mexicana de Ciencias Forestales 11(58):112-133. Doi: 10.29298/rmcf.v11i58.642. [ Links ]

Yao, X., G. Yang, B. Wu, L. Jiang and F. Wang. 2021. Biomass estimation models for six shrub species in hunshandake sandy land in inner Mongolia, Northern China. Forests 12(2):167. Doi: 10.3390/f12020167. [ Links ]

Zhang, L., G. Cui, W. Shen and X. Liu. 2016. Cover as a simple predictor of biomass for two shrubs in Tibet. Ecological Indicators 64:266-271. Doi: 10.1016/j.ecolind.2016.01.009. [ Links ]

Zhao, H., Z. Li, G. Zhou, Z. Qiu and Z. Wu. 2019. Site-specific allometric models for prediction of above-and belowground biomass of subtropical forests in Guangzhou, southern China. Forests 10(10):862. Doi: 10.3390/f10100862. [ Links ]

Recibido: 12 de Mayo de 2021; Aprobado: 31 de Marzo de 2022

^*Autor para correspondencia; correo-e: msalvador@uach.mx

^{Conflicto de interés}

Los autores declaran no tener conflicto de intereses con persona e institución alguna.

^{Contribuciones por autor}

Margarito Maldonado Ortiz y Martín Martínez Salvador: procesamiento y análisis de los datos, planeación y redacción de manuscrito; Pablito Marcelo López Serrano: coordinación general del proyecto y apoyo para almacenamiento de información; Ricardo D. Valdez Cepeda: análisis de datos; Ricardo Mata González: revisión y corrección de la contribución; Fabián García González: revisión y corrección del documento.

Este es un artículo publicado en acceso abierto bajo una licencia Creative Commons