Glosario
Ametropías |
Defectos de refracción en el ojo que impide que las imágenes se formen debidamente en la retina. |
Facodenesis |
Movimiento del cristalino. |
Fáquico |
El ojo conserva el cristalino. Se añade el sistema óptico sin sustituir nada. |
Miosis pupilar |
Contracción y dilatación de la pupila. |
MOR |
Movimiento Ocular Rápido. |
REM |
Rapid Eye Movement. |
Introducción
En pacientes con ametropías elevadas, es usual implantar lentes fáquicos de cámara anterior con anclaje iridiano (Verisyse® / Artisan®). De acuerdo con los datos de Kamiya et al.,1 de una muestra de 15011 ojos a los que realizaron cirugía refractiva, sólo en 50 ojos se utilizaron este tipo de lentes. Sin embargo, el 66% de los casos presentan cambios en las líneas de Snellen 3 meses después de la cirugía. Este tipo de lentes intraoculares están asociados a otras problemáticas como: formación de cataratas2, desarrollo de glaucoma3, descompensación corneal4, y pérdida de células endoteliales de la córnea5.
Para analizar las problemáticas descritas, se han desarrollado diferentes investigaciones que muestran que la instalación de lentes intraoculares (LIO) genera perturbaciones de pequeña escala en el flujo del humor acuoso (HA) en la cámara anterior6. Estas perturbaciones provocan alteraciones en la dinámica del HA, modificando los esfuerzos cortantes en el iris τ1 y en la córnea τ2, que se muestran en la Figura 1 Adicionalmente a esto, la presión intraocular puede aumentar tras la implantación del lente y así, generar condiciones patológicas que afecten tanto al iris como a la córnea. La mayoría de los estudios consideran que la topografía del iris es simétrica; sin embargo, en la realidad, esta condición no se cumple, lo que podría ocasionar una modificación del flujo, promoviendo daños en las estructuras de la cámara anterior6, 7, 8.
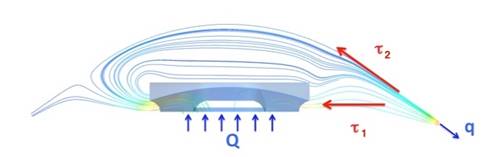
Figura 1 Diagrama de fuerzas y flujos. Esfuerzos cortantes en el iris τ1 y en la córnea τ2. Flujo de entrada, Q, flujo de salida, q.
En los últimos años se han realizado estudios analíticos y numéricos del flujo del humor acuoso dentro del ojo9,10,11. Siggers y Ethier12 presentan una amplia revisión de los mecanismos asociados a la dinámica de fluidos dentro del ojo. Por otra parte, Fitt y Gonzalez13, mencionan la existencia de cinco tipos de mecanismos físicos responsables del flujo del HA dentro de la CA: (i) Flujo por flotación debido a la diferencia de temperatura entre la superficie anterior de la córnea y el iris; (ii) flujo generado por la producción de humor acuoso en el cuerpo ciliar; (iii) flujo generado durante el sueño, en la posición boca arriba, (iv) flujo generado por movimiento rotatorio rápido de los ojos (REM), y (v) flujo generado por facodonesis. En cuanto al humor acuoso, en el estudio publicado por Canning et al.,9 consideran que presenta propiedades muy similares a las del agua. Tomando esto en consideración, realizaron un estudio analítico y numérico en el que encontraron que la máxima velocidad del flujo es de 7.5 x 10-6. Por otra parte, Karampatzakis y Samaras14 generaron un modelo numérico que describe la transferencia de calor en el ojo humano, tomando en cuenta el movimiento del HA en la cámara interior. Observaron que la mecánica del humor acuoso altera la distribución de temperaturas en la superficie de la córnea y cristalino. Este análisis determinó que la velocidad máxima del flujo en la cámara anterior es de 3.36 x 10-4 m/s.
De manera similar, Repetto et al.6 realizaron un estudio utilizando un modelo matemático con el que describen el flujo del HA en la CA en presencia de un LIO. Para su análisis, consideraron cuatro tipos de mecanismos de producción de flujo del humor acuoso: (i) Por miosis pupilar; (ii) flujos producidos por flotación causados por un diferencial de temperatura, (iii) por movimiento rotatorio de los ojos, y (iv) por producción y drenaje del HA. Estos cuatro mecanismos los analizan por separado. En sus resultados observaron que la presencia del LIO genera modificaciones significativas en la dinámica del fluido, mas no en la presión intraocular, esto se mantiene para cualquier tipo de mecanismo. Además, para el caso del flujo promovido por fuerzas de flotación, determinaron que el esfuerzo cortante máximo en la pared anterior de la córnea es de 1.62 x 10-3 Pa, cuando no hay lente y de 1.19 x 10-3 Pa, cuando el lente está presente. Mientras que el esfuerzo cortante máximo en el iris, cuando hay lente, para el mismo caso de movimiento por flotación es de 2.55 x 10-3 Pa. No se reporta el valor cuando no hay lente. En experimentos in vitro, se ha reportado desprendimiento de células a valores de esfuerzo cortante de 0.03 Pa6; por lo que en ningún caso, los esfuerzos cortantes ponen en riesgo la integridad de la córnea ni del iris. A diferencia de Fitt y Gonzalez13, Repetto et al.6 mencionan que la máxima velocidad localizada es cuando se realiza el metabolismo de producción y drenaje de HA, con un valor de 5.89 x 10-5 m/s. En todos los casos anteriores, hacen el análisis del flujo considerando que la geometría del ojo es simétrica.
En el presente estudio, se muestra una metodología para evaluar lentes fáquicos de cámara anterior con anclaje iridiano (Verisyse® / Artisan®), cuando el flujo presenta condiciones asimétricas. El principal objetivo es el de determinar la influencia que tienen las asimetrías en el flujo del HA dentro de la cámara anterior en el esfuerzo cortante sobre la córnea y el iris. Para describir el fenómeno, se emplearán métodos numéricos para simular el flujo, considerando que el humor acuoso se comporta como un fluido newtoniano incompresible con propiedades constantes. La forma del ojo se obtuvo de Repetto et al.,6 mientras que la forma del lente se obtuvo de Tychsen et al.8
Metodología
Hasta el momento, no es posible valorar la influencia que tiene un lente intraocular in vivo, por lo que se requieren de metodologías que puedan determinar los esfuerzos cortantes en el iris y la córnea en presencia LIO. En el presente trabajo se realiza un análisis empleando el método de elemento finito que permitirá evaluar las condiciones de forma personalizada en cada paciente. Para esto, se plantea analizar el flujo del humor acuoso en el ojo con un lente intraocular y sin lente, como se muestra en la Figura 2.
Las ecuaciones que describen el movimiento del humor acuoso dentro de la cámara anterior son la ecuación conservación de masa y las ecuaciones de Navier Stokes, esto es:
Donde u es el vector de la velocidad del humor acuoso, P es la presión,
Las dos ecuaciones anteriores están sujetas a las siguientes condiciones de frontera: a) el humor acuoso entra a la cámara anterior por la región central a una velocidad o flujo conocido; b) la salida del humor acuoso es por el ángulo formado entre la córnea y el iris, lugar donde se encuentra la red trabecular donde se impone un valor de presión venosa; y por último, c) se considera la condición de no deslizamiento en las fronteras con la córnea y el iris.
Dentro de las estructuras para drenar el humor acuoso el ojo cuenta con canales colectores que están ubicados a lo largo del canal de Schlemm. Cha et al.15 y Hann et al.16 mencionan que los canales colectores están distribuidos de forma aleatoria, lo que genera perturbaciones en el flujo generando asimetrías. Para realizar el análisis, se inducen asimetrías en el flujo modificando las condiciones de salida del HA. Para esto, el ojo se divide en dos mitades y se definen zonas en el ángulo por donde no se permite la salida del fluido.
Se propone un caso simétrico y tres casos asimétricos: en el primer caso asimétrico, se cierra la mitad, en el segundo caso, un tercio y en el último caso, un cuarto del ángulo de salida de una mitad del ojo. Esto se puede observar en la Figura 3.
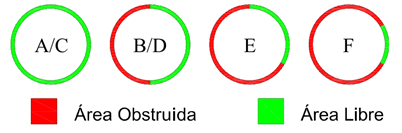
Figura 3 Casos de análisis en el que se muestran las zonas abiertas y cerradas de ángulo entre la córnea y el iris.
Las dimensiones del LIO son: Largo, 8.5 mm; diámetro del lente plano cóncavo, 5 mm; alto del lente, 0.95 mm. Dicho lente se encuentra situado a 0.7 mm del cristalino y a 0.62 mm del iris.
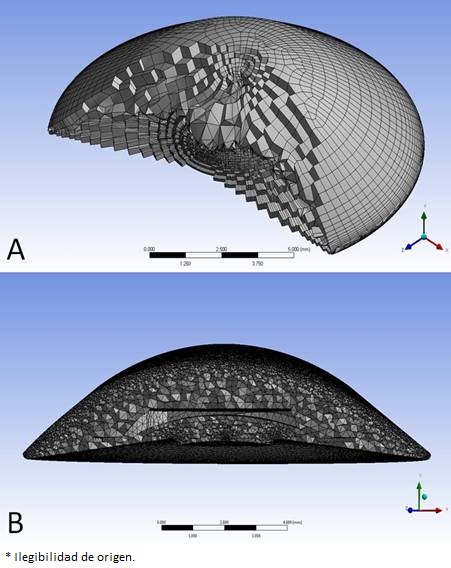
Para realizar la simulación numérica se utilizaron dos mallas, Figura 4. La primera malla, Figura 4A, es para el caso de estudio sin lente; mientras que la segunda es para el caso en presencia del lente, Figura 4B.
La primera malla se conforma por 147,547 elementos y 111,127 nodos, mientras que la segunda cuenta con 2,298,556 elementos y 435,081 nodos. La diferencia de elementos y de nodos se debe a la presencia del lente y que se requiere un refinamiento cerca del mismo. Para determinar la malla, se realizó un análisis de sensibilidad con tres discretizaciones diferentes, sin que se obtuviera diferencias significativas entre los resultados; por lo que no se requieren más mallas. La malla final se obtuvo hasta no encontrar diferencias entre las soluciones.
Para todos los casos analizados se realizan las siguientes consideraciones: (i) El flujo de entrada del humor acuoso, Q, es por el área donde se ubica la pupila, se toma un valor constante de 5 x 10-8 kg/s, de acuerdo con Fitt y Gonzalez13; (ii) el humor acuoso es un fluido newtoniano con propiedades constantes (ρ = 1000 Kg/m 3 y μ = 1x10-3 N·s·m -2); (iii) se analiza en un régimen estacionario; y por último, (iv) las paredes de la córnea y del iris son fijas y rígidas. Cabe destacar que en condiciones fisiológicas normales el flujo de humor acuoso que entra al ojo es el mismo que se drena por las diferentes estructuras, q12. Debido a que el objetivo del estudio es analizar la influencia de las asimetrías, se propone que esta condición se mantenga con el fin de aislar dicha variable.
Para validar la simulación numérica del presente estudio, se compararon los resultados obtenidos con los trabajos de Fitt y Gonzalez13, Repetto et al.,6 y con los valores mostrados por Siggers y Ethier12. Para el primer caso se dibujó la geometría propuesta en13, considerando que se tiene una velocidad de entrada del humor acuoso en función del radio de la pupila u = K1(b
2 - r
2); donde K1 es una constante, el valor de la constante es de K1 = 0.23 m
-1
s
-1, que corresponde a un flujo volumétrico de secreción de 1.23 μl/min; b es el radio de la región de la pupila, b = 0.00275 m; y r es la coordenada radial. Usando estos datos se determinó una velocidad máxima de 5.48 x 10-6
m/s. Cuando se considera que la velocidad del humor acuoso a la entrada es constante, u = 8.625 x 10-7
m/s (manteniendo el mismo flujo volumétrico del caso anterior), se obtiene una velocidad máxima en la cámara anterior de 1.82 x 10-6
m/s
Al usar la geometría reportada por Repetto et al.6 en conjunto con la función de velocidad de entrada descrita anteriormente, resulta en una velocidad máxima de
Resultados y Discusión
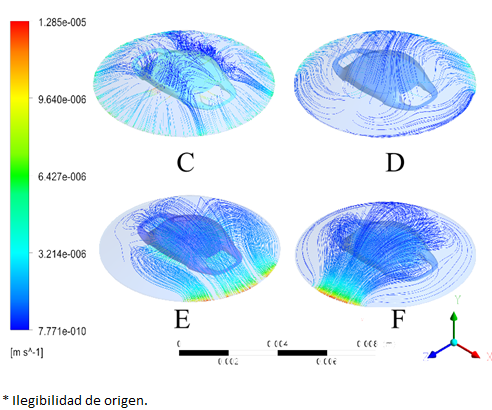
Se obtuvieron resultados del movimiento del humor acuoso para diferentes casos, así como la presión en la cámara anterior, el esfuerzo cortante en la córnea y el iris. En la Figura 5, se pueden observar las líneas de corriente del humor acuoso dentro de la cámara anterior para un caso simétrico y uno asimétrico.
Al comparar los resultados de ambos análisis sin LIO, se aprecia que las líneas de flujo en el caso simétrico son prácticamente uniformes y con velocidad constante. Sin embargo, al observar los resultados en configuración asimétrica, se aprecia una redirección del fluido y un aumento de velocidad del 78.5% con respecto al caso simétrico debido a la reducción del área de salida, y por efecto de conservación de la materia se debe incrementar la velocidad. La Figura 6 muestra los resultados de todas las condiciones descritas en la Figura 3.
Se pueden apreciar perturbaciones en el flujo del humor acuoso debido a la presencia del Lente Intra Ocular (LIO), ya que el lente se convierte en una barrera para que el humor acuoso entre a la cámara anterior, incrementando la resistencia al flujo y modificando las líneas de corriente con respecto al caso sin LIO. De igual manera que el caso sin LIO, existe un aumento en la velocidad de salida del flujo para todos los casos; esto se debe a la reducción del área por donde sale el humor acuoso, generando un aumento máximo del 384.7%, con respecto al flujo simétrico con LIO, este es el caso D de la Figura 6.
Para todos los casos sin lente, los esfuerzos cortantes sobre la superficie del iris generado por el flujo del humor acuoso se pueden apreciar en la Figura 7. Es evidente que el esfuerzo cortante máximo se encuentra en la superficie del iris cercana a la zona de salida. Se observa que en el caso asimétrico se tiene un aumento del esfuerzo cortante de 82.1% con respecto al caso simétrico. Sin embargo, estos valores no son suficientes para ocasionar daño en la estructura del iris, de acuerdo con los valores críticos obtenidos por Repetto et al.6
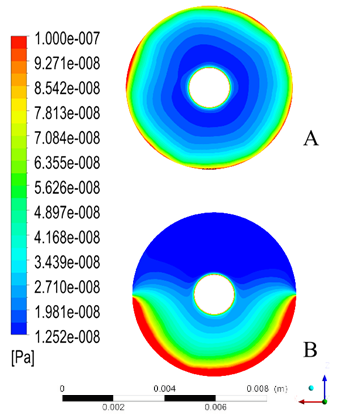
Figura 7 Visualización de los esfuerzos cortantes en la pared presentes en la superficie del iris en ausencia del LIO.
Por otra parte, al analizar los resultados en presencia del LIO, se observa un aumento del 377.1% del esfuerzo cortante máximo en la pared en la superficie del iris, en el caso donde la obstrucción a la salida del humor acuoso es más grande, ver Figura 8.
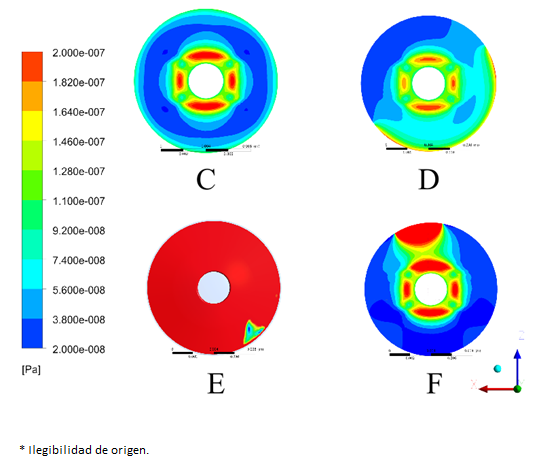
Figura 8 Visualización de los esfuerzos cortantes en la pared (WallShear) presentes en la superficie del iris en presencia del LIO.
También se puede observar que en el caso simétrico con LIO, se obtiene una distribución de esfuerzos cortantes igualmente simétrico. Esto contrasta con el resultado sin LIO, que presenta ligeras asimétricas para el caso en que la salida es totalmente abierta. Cabe destacar que el esfuerzo cortante máximo del caso B Fde la Figura 9, es menor que el esfuerzo máximo del caso simétrico, Figura 9A.
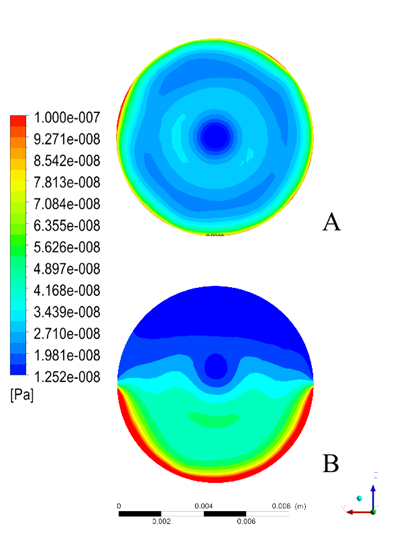
Figura 9 Visualización de los esfuerzos cortantes en la pared presentes en la superficie anterior de la córnea en ausencia del LIO.
Esto es de llamar la atención, ya que indica la existencia de una distribución de la salida en la que se tiene un esfuerzo cortante óptimo.
Los esfuerzos cortantes en la pared de la superficie anterior corneal, son similares a los del iris.
De igual manera, tiene el mismo porcentaje de aumento en el esfuerzo cortante para los modelos plateados con respecto al caso simétrico.
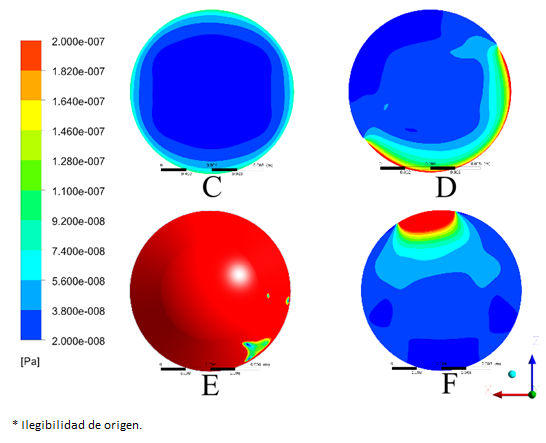
Figura 10 Visualización de los esfuerzos cortantes en la pared presentes en la superficie anterior de la córnea en presencia del LIO.
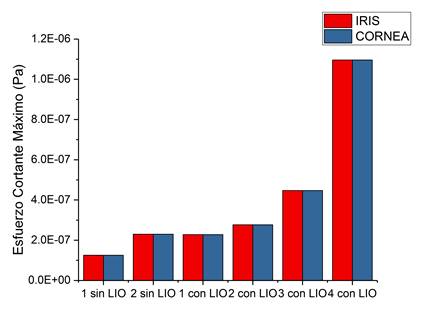
En la Figura 11 se observa un comportamiento peculiar. Se esperaba que al reducir el área de salida del humor acuoso, la magnitud del esfuerzo cortante promedio sobre el iris se incrementaría, sin lente y con lente.
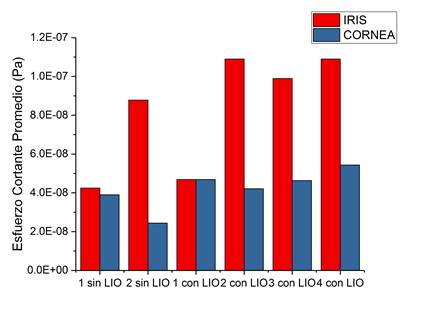
Figura 11 Comparación de esfuerzo cortante promedio en la superficie de la córnea para todos los casos.
Esto se cumple para el caso sin lente. Sin embargo, para los casos con lente se observa un incremento del esfuerzo cortante entre el caso 1 y el caso 2, mostrados en la Figura 3, y posteriormente se observa una reducción entre el caso 2 y el caso 3, descritos en la misma Figura 3. Este comportamiento es atípico, y muestra la presencia de un posible punto óptimo. También se aprecia que el caso simétrico completamente abierto presenta el menor valor de esfuerzo cortante promedio con y sin lente. Esto se tradujo en que al encontrar una pequeña obstrucción en la salida del humor acuoso, se presenta un incremento del esfuerzo cortante de más del doble, por ejemplo en el caso 2 con LIO.
Con respecto al esfuerzo cortante sobre la córnea, la presencia del lente intraocular disminuye el valor promedio de dicho esfuerzo, esto se ve en los resultados del caso 1 y el caso 2 sin LIO de la Figura 11. Esto es atribuible a que se tiene un lado completamente cerrado; por lo que el flujo se concentra en una mitad, mientras que en la otra no se presentan movimientos significativos, por lo que la córnea no está sujeta a esfuerzo cortante. En los casos con LIO se obtiene el comportamiento esperado; esto es, que al reducir el área de salida del HA el esfuerzo cortante promedio se incrementa (caso 2 al caso 4 con LIO). Sin embargo, nuevamente se observa una reducción entre el caso completamente abierto, caso 1 con LIO, y el caso con una mitad cerrada, caso 2 con LIO.
El esfuerzo cortante máximo en el iris y en la córnea reportados por Villamarin et al.7 son de 5 x 10-4 Pa y 6.5 x 10-4 Pa, respectivamente. Por otra parte, Kumar18 reporta un esfuerzo cortante máximo en el iris de 2.17 x 10-3 Pa, considerando un flujo por flotación debido a una diferencia de 2°C. Por último, Repetto et al.13 reportan un esfuerzo cortante máximo en la córnea sin el lente intraocular de 1.62 x 10-3 Pa y de 1.19 x 10-3 Pa en presencia de lente intraocular. Estos resultados contrastan con los obtenidos en el presente estudio, Figura 12, ya que en los casos analizados los esfuerzos cortantes promedio y máximos en la córnea se incrementan cuando se tiene al lente intraocular con respecto a los resultados sin el lente. Estas diferencias son atribuibles a las fuerzas que producen al humor acuoso; mientras que en el caso del presente análisis el movimiento se debe a la entrada de humor acuoso a la cámara anterior, en Fitt y Gonzalez13 el movimiento del humor acuoso es motivado por una diferencia de temperaturas.
Conclusión
El presente trabajo muestra una metodología para evaluar la influencia que tiene un lente intraocular en la dinámica del humor acuoso. Mediante la simulación se puede evaluar el esfuerzo cortante en la c\'ornea y en el iris en presencia de un LIO; además de las perturbaciones en el movimiento del humor acuoso debidas a la presencia del lente. Para validar la simulación numérica se compararon las velocidades con las obtenidas por Fitt y Gonzalez13 y Repetto et al.6 A pesar de que la geometría del ojo se obtuvo de Repetto et al.6, sólo fue posible comparar con uno de los casos estudiados por el trabajo citado, debido a que ellos consideran efectos de flotación por diferencia de temperatura, así como el flujo generado por movimiento rotatorio rápido de los ojos y flujo generado por facodonesis.
A partir de los resultados obtenidos, se observa que los esfuerzos cortantes máximos son proporcionales al área de salida del humor acuoso que está obstruida para ambos casos: sin lente y con lente, tal como se ilustra en la Figura 12. Esto contrasta con los resultados de esfuerzo cortante promedio, Figura 11, en la que el esfuerzo cortante promedio en el iris sin lente intraocular se incrementa al reducir el área de salida del humor acuoso, mientras que en la córnea el esfuerzo cortante disminuye para el mismo caso. Por otra parte, cuando se tiene el lente intraocular, en el caso del iris se observa que el esfuerzo cortante crece significativamente cuando hay asimetrías inducidas por la reducción de área de salida; sin embargo, el incrementar el área obstruida no tiene un efecto significativo en el esfuerzo cortante medio en el iris. En lo que respecta a la córnea se encontró un esfuerzo cortante mínimo para el caso en que se tiene bloqueada el 50% del área de salida. Los resultados del esfuerzo medio en la córnea con lente se pueden ajustar mediante una curva cuadrática, mientras que los datos en el iris, no presentan correlación alguna.
Los resultados muestran que las asimetrías en el flujo del humor acuoso, inducidas por las restricciones de salida del fluido, tienen una gran influencia en la distribución de velocidades y en los esfuerzos cortantes en el iris y en la córnea, incrementándose hasta 5 veces el valor de referencia. Sin embargo, los esfuerzos cortantes no causan daños estructurales a los tejidos oculares, al ser menores al valor umbral de 0.03 Pa. El presente modelo es susceptible a mejoras, ya que no se consideran los movimientos del humor acuoso debidas a las diferencias de temperaturas ni a movimientos rotatorios del ojo ni la facodonesis. Esto queda como trabajo a futuro para poder evaluar si los lentes fáquicos de cámara anterior podrían causar daños posteriores a su instalación, de acuerdo a la topología del ojo.











 nueva página del texto (beta)
nueva página del texto (beta)