INTRODUCCIÓN
La ciudad de México es la segunda ciudad en Latinoamérica con mayor número de huertos urbanos, que no solo tienen una función estética, sino que también juegan un papel fundamental en la reducción de la isla de calor y en el abastecimiento de hortalizas a nivel local (Punto Periferia, 2021). Sin embargo, el problema es que en algunos huertos el riego se realiza utilizando agua potable y sin una programación del riego (Antonio y col., 2023). Por esta razón, es indispensable la cuantificación de la evapotranspiración de referencia (ETo), para la estimación de los requerimientos hídricos de los cultivos. La ETo indica el volumen de agua perdida por la vegetación natural o pasto de referencia a una altura de 0.12 cm (Allen y col., 1998). Es el proceso hidrológico más difícil de estimar y es fundamental en el mecanismo para la creación de precipitación (Gordillo y col., 2014). De acuerdo con Walls y col. (2020) la ETo devuelve más del 60 % de la precipitación anual a la atmósfera a nivel mundial, su estimación se realiza a través del uso de mediciones in situ o datos meteorológicos disponibles.
La evapotranspiración de referencia es un proceso no lineal, complejo e inestable, por lo que es difícil derivar una fórmula precisa para representar todos los procesos físicos involucrados (Gonzalez y col., 2008). El método recomendado por la Organización de las Naciones Unidas para la Alimentación y la Agricultura, conocida como FAO, requiere de numerosos parámetros y variables climatológicas que en ocasiones, aparecen como datos faltantes en las estaciones meteorológicas. Con el fin de tratar este tipo de problema, surgen modelos alternativos, como las redes neuronales artificiales (RNA), que forman parte de la inteligencia artificial y son modelos que tienen la capacidad de aprender la relación subyacente entre entradas y salidas de un proceso, a partir de datos históricos, sin las reglas físicas que se adjuntan explícitamente (Moghaddamnia y col., 2009). Las RNA tienen la capacidad de llevar a cabo un mapeo no lineal, de un espacio de entrada m-dimensional a un espacio de salida n-dimensional, sin el entendimiento del proceso físico que se está modelando, y se desarrolla basado en modelos matemáticos, en donde la elección del modelo de RNA depende del conocimiento a priori del sistema a modelar (Boussaada y col., 2018). Este tipo de técnicas se han utilizado con éxito en la modelación de series de tiempo complejas altamente no lineales, en una gran variedad de campos del conocimiento (Sudheer y col., 2003). Las más utilizadas son estáticas del tipo perceptrón multicapa (MLP, por sus siglas en inglés: Multilayer Perceptron) con alimentación hacia delante (FFNN, por sus siglas en inglés: Feedforward Neural Network).
Kumar y col. (2002) y Kisi (2006) mostraron que la estimación de la ETo, utilizando RNA con datos meteorológicos, es más precisa que otros métodos convencionales, como la ecuación de Penman-Monteith y Ritchie. Kisi (2006) comparó el desempeño de una RNA con los métodos de Penman-Monteith y los modelos empíricos de Ritchie y Hargreaves-Samani, utilizando 4 entradas (radiación solar, temperatura, humedad relativa y velocidad del viento) y dos entradas (radiación solar y temperatura). Los dos modelos de redes de MLP tuvieron un desempeño superior que el resto de los modelos, con un R2 de 0.986 y 0.854, respectivamente. Moghaddamnia y col. (2009) hicieron una comparación del MLP con tres modelos empíricos y demostraron que las RNA tuvieron un desempeño mucho mejor (R2 = 0.97) al obtenido con los modelos empíricos de Hefner, Lincare y Marciano (R2 entre 0.23 y 0.54). Asimismo, Rahimi-Khoob (2008) comparó la RNA MLP con el método de Hargreaves para estimar ETo y confirmó que la red MLP con FFNN, tiene una alta precisión para la estimación de ETo. En un estudio reciente, Abrishami y col. (2019) utilizaron una red MLP para estimar la ETo con varias opciones de variables de entrada y diferentes funciones de activación, obteniendo R2 mayores a 0.94 en la etapa de entrenamiento. Estos estudios indican que, las RNA más utilizadas son las del tipo de MLP con FFNN. Este tipo de redes se pueden mejorar haciendo un pequeño cambio en la arquitectura: cuando a las redes FFNN se les agrega retroalimentación de las capas ocultas hacia la capa de entrada, se genera una red recurrente más simple, llamada red neuronal recurrente Elman (ERNN, por sus siglas en inglés: Elman Recurrent Neural Network), la cual tiene memoria de los eventos inmediatos anteriores, y eso le permite tener mejores resultados que las redes FFNN.
Ghose y col. (2018) utilizaron la ERNN para predecir la profundidad del nivel freático mediante diferentes combinaciones de las variables escurrimiento, temperatura, humedad, precipitación y evapotranspiración, en Odisha, India, obteniendo un buen desempeño en la etapa de prueba, con coeficientes de determinación entre 0.9 y 0.92. También Zhao y col. (2022) utilizaron la RNA ERNN para predecir la ETo en diferentes zonas climáticas en China. Los autores afirman que la red ERNN tiene mayor poder computacional y estabilidad que las FFNN.
Un tipo de red recurrente, más compleja que la red ERNN, es la red dinámica recurrente denominada red Autorregresiva No Lineal con Entradas Exógenas (NARX, por sus siglas en inglés: Nonlinear Autoregressive Model with Exogenous inputs), o también llamada, red neuronal recurrente con retrasos en el tiempo, que tiene retroalimentación entre todos los elementos que la conforman, realiza el intercambio de información entre neuronas de una manera mucho más compleja y puede propagar información hacia adelante en el tiempo, lo que la hace útil en la predicción de eventos (Bianchi y col., 2017). Proias y col. (2020) implementaron la red NARX para predecir la ETo en Velestino, Grecia, utilizando como variables de entrada precipitación, temperaturas máxima y mínima, humedad relativa máxima y mínima, velocidad del viento y radiación solar. Los autores obtuvieron valores de R2 de 0.77 y 0.75 en la predicción de 2 d y 3 d adelante, y encontraron que ETo es más sensible a la radiación y menos sensible a la velocidad del viento.
En los estudios que se han utilizado modelos de RNA para la predicción de la ETo se comparó el desempeño de alguna red del tipo FFNN, ERNN o NARX con métodos empíricos; sin embargo es necesario comparar el desempeño de estas redes en la predición de la ETo.
El objetivo del presente trabajo fue estimar la evapotranspiración de referencia (ETo) utilizando la ecuación de Penman-Montieth, a fin de desarrollar modelos de redes neuronales artificiales (RNA) que permitan predecir la ETo en regiones con información climatológica limitada, y su vez comparar el desempeño de tres modelos de RNA: FFNN, ERNN y NARX.
MATERIALES Y MÉTODOS
Adquisición de datos
Para el presente estudio, se utilizaron datos diarios de temperatura mínima y máxima (Tmin, Tmax), humedad relativa mínima y máxima (HRmin, HRmax), velocidad del viento (u) y radiación solar (Rad), durante el periodo del 1 de enero de 2007 al 31 de diciembre de 2018. Se procesaron 4 383 patrones de datos, provenientes de dos estaciones meteorológicas establecidas en la alcaldía Álvaro Obregón en la CDMX: ENP8, ubicada en 19º21’00’’ N y 99º11’24’’ W, con una altitud de 2 316 msnm; y ENP4, ubicada en 19°24’00’’ N y 99°11’24’’ W, con una altitud de 2 307 msnm (Instituto de Ciencias de la Atmósfera y Cambio Climático, 2018).
Cálculo de la evapotranspiración de referencia (ETo)
La ETo diaria, que será empleada como salida en los modelos de RNA, se obtuvo utilizando el método de Penman-Monteith, recomendado por la FAO (Allen y col., 1998) y descrito en las Ecuaciones 1 a 4. Las variables involucradas se definen en la Tabla 1.
Donde la presión de vapor de saturación media (es):
Presión de vapor real (ea):
Tabla 1 Definición de variables y parámetros involucrados en el cálculo de ETo.
| Símbolo | Definición | Unidades |
|---|---|---|
| ETo | Evapotranspiración de referencia | mm/d |
| ͺΔ | Pendiente de la curva de presión de vapor | kPa/ºC |
| G | Flujo térmico del suelo | MJ/m2/d |
| γ | Constante psicométrica | kPa/ºC |
| u | Velocidad del viento medida a 2 m de altura | m/s |
| T | Temperatura media | ºC |
| ea | Presión de vapor real | kPa |
| es - ea | Déficit de presión de vapor | kPa |
| eo(Tmin) | Presión de vapor de saturación a la temperatura mínima diaria | kPa |
| eo(Tmax) | Presión de vapor de saturación a la temperatura máxima diaria | kPa |
| es | Presión de vapor de saturación media | kPa |
| Tmax | Temperatura máxima | ºC |
| Tmin | Temperatura mínima | ºC |
| HRmax | Humedad relativa máxima | % |
| HRmin | Humedad relativa mínima | % |
| Rad | Radiación neta en la superficie de cultivo | MJ/m2/d |
Análisis de correlación
La selección de las variables de entrada se llevó a cabo considerando el análisis de correlación entre las 6 variables de entrada, descritas al inicio de materiales y métodos y la ETo, que permite encontrar la asociación entre las variables de entrada y salida, lo cual representa una guía en la construcción de los modelos de RNA.
Análisis de sensibilidad
Con el fin de identificar las variables más importantes para predecir la salida, se implementó el método de Garson en la red FFNN con 6 entradas, que utiliza la matriz de pesos entre la capa de entrada y la oculta, y entre la capa oculta y la de salida. Se discrimina la importancia relativa de las variables predictoras para una sola variable de respuesta. La contribución relativa de cada entrada (RIj) está dada por la Ecuación 5 (García y col., 2020).
Donde:
Wij = pesos sinápticos de la conexión de entrada i a la capa oculta j.
Wjo = pesos sinápticos de la conexión capa oculta j a la salida.
m = número de neuronas en la capa oculta.
n = número de capas ocultas.
Modelos de redes neuronales para predecir la evapotranspiración de referencia
Se compararon tres modelos de RNA con la estructura de MLP, para la predicción de la ETo de referencia en la estación meteorológica ENP8: 1) FFNN; 2) ERNN y 3) NARX.
Con base en el análisis de correlación y análisis de sensibilidad de Garson, para los 3 modelos de RNA, se investigaron dos casos: 1) con 6 variables de entrada: Rad, Tmax, Tmin, HRmax, HRmin y u, definidas en la Tabla 1; y 2) con 2 variables de entrada: Rad y Tmax. En todas las RNA implementadas la variable de salida fue la ETo diaria.
De acuerdo con Abrishami y col. (2018), la mayoría de los investigadores eligen conjuntos de datos de entrenamiento y prueba de 90 % versus 10 %, 80 % versus 20 % y 70 % versus 30 %. Sin embargo, a medida que aumenta el número de patrones de entrenamiento, mejora el desempeño de la RNA en la predicción. Debido a lo anterior, para el presente trabajo, el 90 % de los datos se utilizaron para el entrenamiento de la red (3 943 d: 1 de enero del 2007 al 18 de octubre del 2017), y el 10 % para la evaluación de la red (440 d), que incluye el periodo del 19 de octubre 2017 al 31 de diciembre del 2018, utilizando la red entrenada sin proveer la salida.
Con el fin de hacer una comparación equilibrada de las 3 redes, se utilizó el mismo número de nodos en la capa oculta, los cuales se eligieron de acuerdo a los siguientes criterios:
1) Regla de la pirámide geométrica (Masters, 1993);
2) Promedio entre el número de nodos en la capa de entrada y la capa de salida
3) Teorema de Kolmorogov (Kůrková, 1992);
4) Regla empírica
Donde:
n = número de neuronas de entrada.
m = número de neuronas de salida.
Se compararon 5 algoritmos de entrenamiento: 1) Levenberg-Marquardt (Trainlm); 2) gradiente conjugado escalado (Trainscg); 3) Broyden, Fletcher, Goldfarb, y Shanno (Tranibfgs); 4) gradiente conjugado Fletcher-Powell (Traincgf); y 5) gradiente descendente (Traingd), en combinación con dos algoritmos de aprendizaje: 1) gradiente descendente (Learngd) y 2) gradiente descendente con momento (Learngdm).
En estudios anteriores, realizados para la predicción de la ETo, se utilizó la función de activación de la tangente sigmoidal entre la capa de entrada y la oculta (Huo y col., 2012), la cual se implementó en el presente estudio y se expresa como:
La función de activación entre la capa oculta y la capa de salida fue una función lineal.
RNA con alimentación hacia adelante (FFNN)
La red neuronal del tipo MLP con FFNN, es una estructura que permite aprender cualquier tipo de mapeo no lineal continuo. Se conocen como modelos no lineales, que son capaces de descubrir patrones y simular y pronosticar series de tiempo (Jahani y Mohammadi, 2019). La arquitectura del modelo estático de RNA se refiere a la capa de entrada y salida, número de capas ocultas y el número de nodos en cada una. De acuerdo con Kumar y col. (2002) una capa oculta es suficiente para poder obtener resultados precisos.
El proceso de entrenamiento consiste en modificar los pesos, de tal forma que, generen un error cuadrado medio mínimo (MSE, por sus siglas en inglés: Mean Squared Error) entre la salida real y la predicha por la red. Posteriormente, en la etapa de prueba o evaluación, el desempeño de la red se avalúa con datos no incluidos en la etapa de entrenamiento y se obtiene nuevamente el error. La Figura 1 muestra la arquitectura de la red neuronal del tipo MLP con FFNN, con las 6 variables de entrada y la salida ETo.
Red neuronal recurrente Elman (ERNN)
La ERNN fue propuesta por Elman (1990) para el procesamiento del habla. Es una red neuronal dinamica recurrente, en donde existe retroalimentacion a diferentes niveles. Cada neurona esta asociada a una neurona de la capa oculta, que se utiliza para recordar información del estado inmediato anterior y puede ser considerada como retraso de un paso. Esta propiedad hace que la red ERNN sea sensible a datos historicos y tiene la funcion de un mapa dinamico de caracteristicas, que es especialmente adecuada para construir modelos de prediccion (Gao y col., 2021).
La capa de entrada y salida y la capa oculta se conectan de igual forma que una red MLP, sin embargo, durante el entrenamiento, se transfiere información de la capa oculta hacia la salida, y también de la capa oculta hacia la entrada de manera recursiva. La información se procesa a través de las funciones de activación (Figura 2). Yun y col. (2021) afirman que esta red es muy sensible a las series de tiempo, debido a la no linealidad dinámica, lo cual la hace eficiente para resolver problemas de predicción dinámica. La expresión de espacio de estado no lineal de la red neuronal ERNN se describe a continuación:
Donde:
y(t) = vector de salida de la red.
x(t - 1) = vector de entrada.
hc(t) = salida de la capa de retroalimentación en el tiempo t.
h(t) = salida de la capa oculta en el tiempo t.
α = factor de ganancia de auto-retroalimentación (0 < α < 1).
Las matrices de pesos entre la capa de entrada a la capa oculta, capa de retroalimentación a la capa oculta y la capa oculta a la capa de salida son Wa, Wb y Wc, respectivamente. Los valores de umbral de la capa oculta y la capa de salida son b1 y b2; f (x) y g (x) son las funciones de transferencia de la capa oculta y la capa de salida.
La actualización de pesos se realiza como:
Donde:
W = peso
E = función objetivo (error cuadrado medio, MSE)
η = paso estudiado.
La red neuronal ERNN ha sido utilizada de manera exitosa por Yun y col. (2021) para un sistema de detección de seguridad, el modelo predice de manera precisa y puede generar “early warnings” para los administradores encargados de la seguridad. Asimismo, Ghose y col. (2018) utilizaron la RNA tipo ERNN para predecir la profundidad en el nivel freático. Dichos autores afirmaron que, una de las ventajas de este tipo de redes es su rápida convergencia, comparada con otras RNA. La estructura de la red neuronal ERNN se puede generar con la función “newelm” de Matlab v2020a.
Modelo de Red Autorregresiva No Lineal con Entradas Exógenas (NARX)
Las redes NARX son redes dinámicas recurrentes, con una o varias capas ocultas y se basan en modelos no lineales de tiempo discreto autorregresivos exógenos (ARX). La recurrencia en la red NARX está dada no solo por la retroalimentación de la salida a las capas intermedias, sino también de la salida a la entrada. Las redes NARX se han empleado en muchos contextos de aplicación diferentes, para pronosticar valores futuros de la señal de entrada (Diaconescu, 2008).
El modelo NARX es muy adecuado para modelar sistemas no lineales y series de tiempo. Boussaada y col. (2018) afirmaron que, el aprendizaje es más efectivo en las redes NARX que en otras redes neuronales y la convergencia es más rápida. Los modelos NARX pueden aplicarse a una gran variedad de sistemas dinámicos no lineales, tienen la habilidad de almacenar en su memoria valores pasados, a fin de predecir valores futuros. Bianchi y col. (2017) mencionaron que los modelos NARX tienen muy buen desempeño en la predicción de series de tiempo altamente no lineales.
La ventaja de las redes NARX es que se pueden implementar como MLP, el próximo valor de salida y(t) se expresa en (12).
Donde:
θ(.) = función de mapeo no lineal desempeñada por MLP.
dx y dy = retrasos en el tiempo de las entradas y salidas.
Las entradas en la red NARX son dos líneas de retraso (TDL, por sus siglas en inglés Tapped-Delay Lines) descritas en (13).
Las ecuaciones en diferencias que gobiernan el modelo NARX son:
Donde:
h1 [t] = salida de la 1ª capa oculta.
hl [t] = salida de la lª capa oculta al tiempo t .
g(.) = función lineal.
f(.) = función de transferencia, que puede ser la función sigmoidal o la tangente hiperbólica.
θi = pesos entre la capa de entrada y la 1ª capa oculta.
θ0 = pesos entre la última capa oculta y la capa de salida.
θhl = pesos entre las capas ocultas sin incluir la capa de entrada y la de salida.
La arquitectura tipo NARX tiene recursividad de la salida final hacia la entrada y, además, con retrasos en entradas y salidas (Figura 3). La ventaja de la red NARX, en comparación con la red ERNN, es que en la etapa del entrenamiento, la retroalimentación se desconecta y funciona como una red FFNN, utilizando valores reales de y(t) en lugar de valores estimados por la red y, una vez entrenada, se vuelve a conectar la retroalimentación de la salida hacia la entrada, para poder predecir el siguiente valor de y(t) (Bianchi y col., 2017). El modelo NARX se considera un buen predictor de series de tiempo y una generalización no lineal de los modelos ARX y, por lo tanto, es una buena opción para predecir valores de la serie de tiempo ETo.
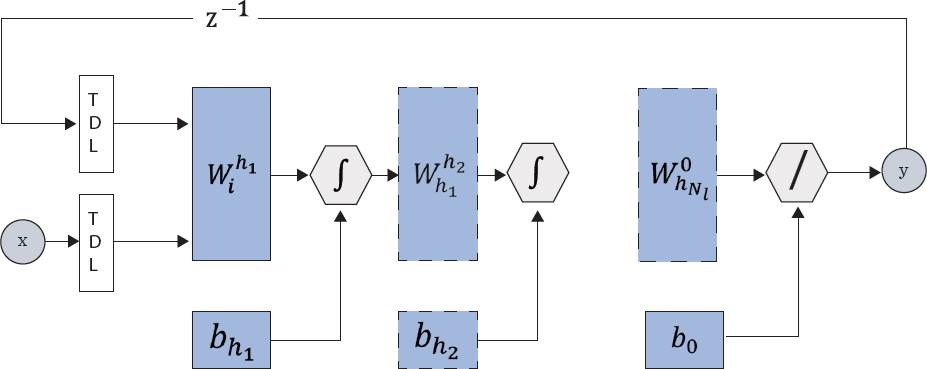
_TDL = Linea de retraso (Tapped Delay Line); x = entradas; y = salidas ;
Figura 3 Arquitectura de la RNA-NARX.
La función newnarx del toolbox Matlab v2020a, crea una red MPL, pero con retroalimentación de la salida hacia la entrada y, además, con retrasos en las entradas y en las entradas provenientes de la retroalimentación.
Todas las simulaciones de redes neuronales se realizaron en Matlab v2020a.
Índices de desempeño de los modelos
El desempeño de los modelos de RNA se midió utilizando los siguientes índices estadísticos (Heng y col., 2009):
1) Índice de eficiencia de Nash-Sutcliffle (E):
Donde:
Po = dato estimado.
P = dato observado.
2) Error medio absoluto (MAE):
3) Error cuadrado medio (MSE):
RESULTADOS Y DISCUSIÓN
Evapotranspiración
Durante el periodo estudiado, 2007-2018, se registró una variación diaria de la ETo en la estación ENP8 entre 0.74 mm/d a 5.96 mm/d, con media de 3.4 mm/d, desviación estándar de 0.8 mm/d y coeficiente de variación (CV) de 24.5 %. Mientras que en la estación ENP4, la ETo varió entre 0.7 mm/d a 4.8 mm/d, registrando una media de 2.99 mm/d, desviación estándar de 0.7 mm/d y coeficiente de variación de 23.6 %. La ETo acumulada en el año 2018, en las estaciones meteorológicas ENP8 y ENP4, fue de 1 295 mm y 1 121 mm, respectivamente, la cual estuvo muy por debajo de la reportada por Ruiz y col. (2015), para una estación cercana a la CDMX (1 419 mm).
Análisis de correlación
La Figura 4 muestra la matriz de correlaciones entre todas las variables utilizadas en los modelos de RNA. Existió una correlación muy fuerte entre la ETo con la Rad (r = 0.91) y Tmax (r = 0.85). La Tmin se correlacionó con la ETo en mucho menor medida (r = 0.21). Estos resultados indican que, un modelo de RNA que incluya a las variables Rad y Tmax podría generar buenos resultados predictivos.
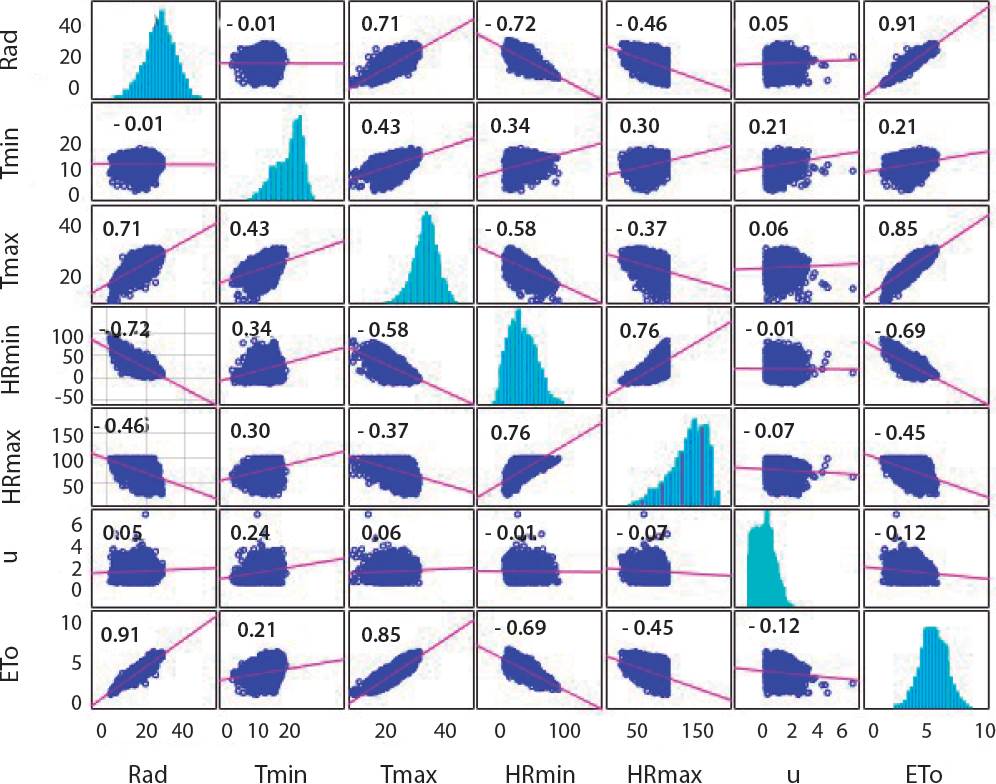
Figura 4 Matriz de correlación entre las variables climatológicas y la evapotranspiración potencial.
La HRmax y HRmin tuvieron una correlación moderada negativa con la ETo. El uso de estas variables, junto con la velocidad del viento, podría parecer redundante en el modelo de RNA, sin embargo, Walls y col. (2020) afirmaron que, a diferencia de los modelos de regresión lineal múltiple, la multicolinealidad (alta correlación entre más de dos variables explicativas) no afecta a los modelos de RNA.
Análisis de sensibilidad por el método de Garson
Los resultados del análisis de sensibilidad, por el método de Garson, aplicado a la red FFNN, se despliegan en la Figura 5. Las variables más importantes en la predicción de la ETo fueron la Rad y Tmax, lo cual coincide con el análisis de correlación. Meneses y col. (2020) estimaron la ETo con el método de PenmanMonteith, para después aplicar un modelo FFNN para la predicción de esta variable. Los autores mencionaron que, una de las dificultades más grandes en la estimación de la ETo es que requiere un gran número de variables climáticas, que en ocasiones no se encuentran disponibles en las estaciones meteorológicas. Por ese motivo, utilizaron únicamente Tmax y Tmin en la estimación de la ETo, el modelo pudo explicar 91.2 % de la variación de la ETo. Asimismo, reportaron que las variables con la mayor sensibilidad fueron la Tmax y Tmin, sin embargo, no consideraron a la Rad.
Zanetti y col. (2007) utilizaron, en el modelo de RNA, la Tmax y Tmin para predecir la ETo en dos estados de Brasil, y demostraron la superioridad de los modelos de RNA (MSE varió entre 0.039 a 0.356), comparados con el método empírico de Hargreaves (MSE osciló entre 0.859 a 0.962). Proias y col. (2020) encontraron que ETo era más sensible a la Rad y menos sensible a la u. Por otro lado, Kisi (2006) estimó la ETo, utilizando RNA con diferentes combinaciones de datos climáticos diarios de Rad, T, HR y u, y demostró que la RNA, únicamente con dos entradas (Rad y T), tuvieron un R2 de 0.98, igual que los modelos de 3 y 4 entradas, en el periodo de prueba.
Walls y col. (2020) compararon 7 modelos de RNA para predecir la ETo en Canadá, variando las entradas de la red: Rad, T, HR, u y flujo de calor del suelo (G). El modelo que incluyó únicamente Rad y T tuvo un desempeño similar que el de los modelos con más entradas, por lo que los autores afirmaron que, cualquier modelo RNA que incluya radiación neta debe ser capaz de proporcionar una estimación adecuada de la ETo, y que la precisión del modelo puede ser refinada aún más incluyendo la temperatura del aire.
El análisis de correlación y el método de Garson, en el presente trabajo, mostraron que las variables que tuvieron mayor influencia en el comportamiento de la ETo fueron Rad y Tmax. Por esta razón, en los tres modelos de RNA desarrollados, se estudiaron dos casos: 1) RNA con 6 entradas (Rad, Tmax, Tmin, HRmax, HRmin, u), y 2) RNA con 2 entradas (Rad y Tmax).
Número de nodos en la capa oculta y algoritmos de entrenamiento
En la red FFNN, el número de nodos en la capa oculta varió entre 6 y 13, de acuerdo a los criterios descritos en la metodología. Dada la poca diferencia entre las eficiencias (0.982 a 0.983), se utilizaron 7 nodos en la capa oculta, para propósitos de comparación de los tres modelos de RNA.
Al probar los algoritmos de entrenamiento Trainlm, Trainscg, Tranibfgs, Traincgf y Traingd, en combinación con los dos algoritmos de aprendizaje, Learngdm y Learngd, la mayor eficiencia de la RNA se obtuvo con la combinación del algoritmo de aprendizaje Learngdm y el algoritmo de entrenamiento Trainlm. Estos dos algoritmos, de aprendizaje y entrenamiento, fueron utilizados en todos los modelos de RNA.
Resultados del entrenamiento y evaluación de los modelos de RNA
Entrenamiento
En la Tabla 2 se presenta un resumen de los indicadores de desempeño de los 3 modelos de RNA para los dos casos estudiados de 6 y 2 entradas. Durante la etapa de entrenamiento (90 % de los datos de la estación ENP8), la eficiencia obtenida fue superior a 0.98 con 6 entradas y a 0.92 con 2 entradas. Esto indica que, la ETo estimada por los 3 modelos (independientemente del número de entradas) estuvo muy cercana a la ETo calculada con la ecuación de Penman-Monteith. Dichos valores fueron superiores a los obtenidos por Meneses y col. (2020) de 0.912 en un estudio en Baixo Brasil, durante el periodo de 1984-2017, utilizando 3 entradas: Tmax, Tmin y la media. Yohanani y col. (2022) implementaron un modelo de RNA, para estimar la ETo en la costa del mediterráneo en Israel, utilizando como entrada únicamente la Rad y obtuvieron un R2 = 0.88 para periodos cortos, de un mes. Sus resultados confirman los de este estudio, del análisis de correlación y el análisis de sensibilidad de Garson, en el sentido de que, para construir un modelo de RNA, para la predicción de la ETo, es suficiente considerar la Rad y la Tmax.
Tabla 2 Indicadores de desempeño en los tres modelos de redes neuronales con 6 y 2 entradas.
| Modelo de RNA | Desempeño en entrenamiento (90 % datos) Estación ENP8 | Evaluación de las RNA (10 % datos ) Estación ENP8 | Predicción de la ETo con RNA entrenadas (10 % datos) | Predicción de la ETo con RNA entrenadas (10 % datos) | ||
|---|---|---|---|---|---|---|
| 6 entradas | 2 entradas | 6 entradas | 2 entradas | 6 entradas | 2 entradas | |
| FFNN |
EF = 0.982 MAE = 0.083 MSE = 0.012 ITER = 95 |
EF = 0.925 MAE = 0.185 MSE = 0.052 ITER = 37 |
EF = 0.947 MAE = 0.140 MSE = 0.030
|
EF = 0.903 MAE = 0.196 MSE = 0.057
|
EF = 0.646 MAE = 0.366 MSE = 0.182
|
EF = 0.856 MAE = 0.230 MSE = 0.073
|
| ERNN |
EF = 0.987 MAE = 0.084 MSE = 0.012 ITER = 48 |
EF = 0.924 MAE = 0.186 MSE = 0.053 ITER = 20 |
EF = 0.947 MAE = 0.139 MSE = 0.031
|
EF = 0.903 MAE = 0.195 MSE = 0.056
|
EF = 0.677 MAE = 0.354 MSE = 0.166
|
EF = 0.855 MAE = 0.23 MSE = 0.074
|
| NARX |
EF = 0.982 MAE = 0.081 MSE = 0.012 ITER = 90 |
EF = 0.924 MAE = 0.186 MSE = 0.053 ITER = 9 |
EF = 0.942 MAE = 0.141 MSE = 0.034
|
EF = 0.902 MAE = 0.195 MSE = 0.056
|
EF = 0.665 MAE = 0.360 MSE = 0.172
|
EF = 0.854 MAE = 0.229 MSE = 0.075
|
EF = Eficiencia; MAE = Error medio absoluto, MSE = Error cuadrado medio, ITER = Iteraciones.
Evaluación con datos de la estación ENP8
Una vez que las redes fueron entrenadas, su poder predictivo se puede visualizar a través de la etapa de evaluación con el 10 % de la información de la estación ENP8 (440 d) no incluida en el entrenamiento y en donde no se proveen las salidas (ETo). En las columnas 4 y 5 de la Tabla 2 se despliegan los resultados para los 2 casos. En esta etapa, los indicadores de desempeño en la red FFNN y ERNN son prácticamente iguales y disminuyen ligeramente para la red NARX. En general, los indicadores de desempeño disminuyeron en las RNA que utilizaron solo 2 entradas (Rad y Tmax) (Figura 6); sin embargo, en todos los casos se registran eficiencias mayores a 0.9.
Predicción de la ETo para la estación ENP4 utilizando las RNA entrenadas
Las RNA en este estudio presentaron un excelente desempeño en la etapa de entrenamiento y evaluación del modelo, utilizando datos de la misma estación. Además, se demostró que es posible estimar la ETo en estaciones climatológicas, o en regiones que únicamente cuenten con información de Rad y Tmax.
La columna 6 de la Tabla 2 muestra los resultados de la simulación de la red entrenada con datos de la ENP8 y utilizada en la predicción de la ETo en la estación ENP4. La eficiencia obtenida usando 6 entradas fue baja, con un rango de 0.64 a 0.67; sin embargo, al utilizar 2 entradas se obtuvieron valores superiores a 0.85, lo cual puede considerarse satisfactorio como modelo predictivo (Tabla 2, columna 7). Este mejoramiento del desempeño, al reducir las entradas, se podría explicar por el hecho de que los modelos cuentan con menor número de conexiones y pesos, lo que los hace más eficientes en la etapa de evaluación.
La Figura 7 compara los datos reales y los resultados obtenidos de la simulación de la ETo, durante 440 d, en la estación ENP4, utilizando las RNA entrenadas (FFNN, ERNN y NARX) con datos de la estación ENP8 y con 2 entradas Rad y Tmax. Las 3 redes entrenadas tuvieron un buen desempeño en la simulación de la ETo de otra estación (ENP4), aunque la tendencia general fue a subestimar esta variable. La mayor ventaja de las redes recurrentes ERNN y NARX es que requirieron menor número de iteraciones (Tabla 2).
CONCLUSIONES
Los modelos de RNA, estático (FFNN) y los dinámicos (ERNN y NARX), con datos meteorológicos limitados (temperatura máxima: Tmax y radiación solar: Rad) tuvieron menor eficiencia que los modelos de RNA con las 6 variables implicadas en la ecuación de PenmanMonteith. Sin embargo, mostraron ser una herramienta poderosa en la predicción de la evapotrasnpiración (ETo) de referencia, utilizando únicamente como variables de entrada la Tmax y la Rad. Las redes NARX y ERNN alcanzaron el mejor desempeño con menor número de iteraciones. Se demostró que una RNA entrenada puede ser utilizada para predecir la ETo en otra localidad, únicamente con datos de Rad y Tmax, sin necesidad de que estén disponibles las variables climatológicas en las estaciones. Dicha RNA entrenada, se puede emplear para estimar la demanda hídrica de cultivos y con ello, poder realizar una programación del riego.











 nueva página del texto (beta)
nueva página del texto (beta)








