Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería agrícola y biosistemas
versión On-line ISSN 2007-4026versión impresa ISSN 2007-3925
Ing. agric. biosist. vol.12 no.1 Chapingo ene./jun. 2020 Epub 23-Mayo-2022
https://doi.org/10.5154/r.inagbi.2019.02.030
Artículo científico
Colección de energía radiante en CPC mejorada con micropartículas
1Universidad Autónoma Chapingo. Carretera México-Texcoco km 38.5, Chapingo, Estado de México, C. P. 56230, MÉXICO.
Introducción:
El aprovechamiento de la energía requiere que los sistemas de colección mejoren la capacidad de transferencia de calor.
Objetivo:
Evaluar el efecto de la incorporación de micropartículas en el fluido de proceso de un colector parabólico compuesto (CPC) sobre su capacidad de operación.
Metodología:
Se evaluó la operación en cuatro ángulos de inclinación (30, 35, 40 y 45°) de un CPC incorporado con carbón activado (102.2 nm), tinta china (198.4 nm) y partículas de cobre (160.1 nm).
Resultados:
La colección de energía se basó en un mecanismo de convección natural, con coeficiente de película que varió entre 10.6 y 15.8 W·m-2·°C-1. La operación con 30° de inclinación mostró las mejores características de colección de energía radiante, donde la eficiencia de aprovechamiento energético fue de 44.6 % para el sistema basado en agua pura, 61.0 % con partículas de cobre, 63.2 % con carbón activado y 68.4 % con tinta china.
Limitaciones del estudio:
El estudio aporta valores de coeficientes de convección térmica que corresponden a las condiciones particulares evaluadas. Para poder valorar el desempeño del sistema en condiciones distintas, es necesario construir modelos basados en análisis dimensional que permitan evaluar los coeficientes de transferencia de calor en situaciones de uso de variables de operación diversas.
Originalidad:
La incorporación de micropartículas en el fluido de proceso incrementa el potencial de colecta de energía radiante de un CPC.
Palabras clave convección térmica; colector parabólico compuesto; radiación térmica
Objective:
To evaluate the effect of the incorporation of microparticles in the process fluid of a compound parabolic collector (CPC) on its ability to operate.
Methodology:
A CPC incorporated with activated carbon (102.2 nm), Chinese ink (198.4 nm) and copper particles (160.1 nm) was evaluated for operation at four angles of inclination (30, 35, 40 and 45°).
Results:
The energy collection was based on a natural convection mechanism, with a film coefficient that varied between 10.6 and 15.8 W·m-2·°C-1. The operation with 30° inclination showed the best characteristics of radiant energy collection, where the energy efficiency was 44.6 % for the system based on pure water, 61.0 % with copper particles, 63.2 % with activated carbon and 68.4 % with Chinese ink.
Limitations of the study:
The study provides values of thermal convection coefficients that correspond to the particular conditions evaluated. In order to evaluate the performance of the system under different conditions, it is necessary to build models based on dimensional analysis that allow the evaluation of heat transfer coefficients in situations of use of diverse operating variables.
Originality:
The incorporation of microparticles in the process fluid increases the potential for collecting radiant energy from a CPC.
Keywords thermal convection; compound parabolic collector; thermal radiation
Introducción
La escasez de energía y la crisis ecológica son cada vez más graves, por lo que el desarrollo y el uso de nuevas formas energéticas son inminentes, lo que apunta al manejo de la energía solar como una alternativa importante (Wang, Yang, Cheng, Guan, & Yan, 2018). En décadas recientes, ha incrementado la popularidad de la energía solar en múltiples aplicaciones industriales, ya que es una alternativa para generar electricidad (Lewis, 2007), productos químicos (Steinfeld, 2005) o calefacción (Panwar, Kaushik, & Kothari, 2011). Muchos procesos industriales requieren del uso de calefacción y, con pocas excepciones como la generación de vapor a partir de bagazo de caña en los ingenios azucareros (Debernardi-de la Vequia, Ortiz-Laurel, & Rosas-Calleja, 2016), la industria utiliza combustibles fósiles o electricidad para la atención de este tipo de servicios (Elimelech & Phillip, 2011). A nivel de casa habitación, es cada vez más frecuente el uso de sistemas de colecta de energía solar para obtener agua caliente, aunque con requerimientos menos demandantes, pues la temperatura objetivo en el fluido es normalmente menor a 40 °C. Debido a esto, se están realizando importantes esfuerzos para colectar energía radiante, mediante concentradores, y para almacenarla (Xu et al., 2015).
En años recientes, se ha mostrado que el aprovechamiento de la energía radiante se puede mejorar con el uso de partículas sólidas de distinta granulometría (Fang et al., 2013; Neumann et al., 2013; Ni et al., 2015). Incluso, se ha observado que las partículas no requieren tener, estrictamente, una base metálica, pues se ha empleado tinta china incorporada al sistema para generar vapor mediante energía solar (Wang et al., 2018). Hasta ahora, los estudios se han enfocado de manera simple a la variación de temperatura en un fluido receptor, pero no hay trabajos que permitan simular los sistemas con base en coeficientes de transferencia de calor. En tal contexto, el presente trabajo se realizó con el objetivo de evaluar el efecto de la incorporación de partículas sólidas en el fluido de proceso de un colector parabólico compuesto (CPC) sobre su capacidad de operación.
Materiales y métodos
Colector parabólico compuesto (CPC)
Se construyó un sistema de colección de energía radiante basado en la geometría de un CPC (Figura 1), el cual contó con un recipiente para mezclar agua con suspensiones de partículas (TK-001), desde donde se alimentó un recipiente tubular de distribución (TK-004B) y tres tubos colectores de energía radiante (TC-005). Para favorecer la colecta de energía, a lo largo de la longitud de cada tubo se instaló una involuta metálica. El tubo distribuidor, a su vez, se conectó con dos recipientes, destinados al almacenamiento de fluido de proceso (TK-002) y de condensados de vapor (TK-003). La temperatura se registró con termopares tipo J (TE-101) (ARPISA, México) en tres puntos del interior de los tubos colectores y el uso de un sistema de adquisición de datos (AD-001). Los tubos colectores se colocaron de tal manera que se pudieran girar en ángulos de 30, 35, 40 y 45° en relación con el suelo o la fuente radiante, que consistió de lámparas de halógeno de 500 W (modelo 9401610, ARGOS, México) (Figura 2).
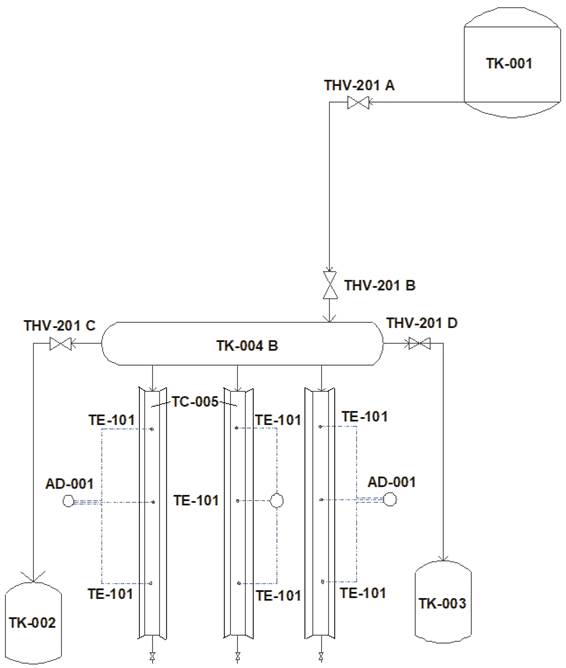
Figura 1 Sistema experimental de colección de energía radiante. TK-001 = tanque de mezcla (agua + partículas); TK-002 = tanque de almacenamiento de fluido de proceso; TK-003 = tanque de almacenamiento de condensados de vapor; TK-004 B = recipiente tubular distribuidor de fluido de proceso; TC-005 = tubos colectores de energía radiante con involutas; THV-201 A, THV-201 B y THV-201 C = válvulas manuales de paso de fluido; THV-201 D = válvula manual de paso vapor; AD-001= sistema de adquisición de datos con registro de tres termopares; TE-101 = termopar tipo J.
Organización experimental
Se evaluó la operación del sistema de colección de energía radiante utilizando agua pura (Ap) como fluido de proceso y agua incorporada con carbón activado (Ca), tinta china (Tc) y partículas de cobre (Nc), en concentración de 0.05 % (Wang et al., 2018). Las partículas de cobre fueron proporcionadas por el Colegio de Postgraduados, México, y se obtuvieron mediante un procedimiento de ablación láser (Bello-Bello et al., 2017). Se colocaron termopares tipo J dentro del tubo concentrador a una distancia de 0.125 m del inicio del tubo, en el centro y a 0.125 m del final del tubo (Figura 1), para registrar la variación de la temperatura del fluido de proceso en función del tiempo. Se condujeron rutinas de captación de energía radiante con registro de la temperatura del fluido de proceso a intervalos de 1 min, en rutinas que duraron entre 140 y 250 min. Se identificó un tiempo característico de estudio de la operación (t est ) y la temperatura alcanzada hasta ese punto (T est ). Asimismo, se determinó el calor absorbido en este periodo (Q abs ), la temperatura de la superficie interna de la pared del tubo contenedor (T P ) y el coeficiente de convección térmica interno (h i ). Todas las rutinas se realizaron por triplicado.
Tamaño de partícula
Se evaluó el diámetro de las partículas incorporadas al fluido de proceso mediante un microscopio electrónico de transmisión (FEI, Tecnai G2 Spirit MIC-E-004, Australia). Para ello, se diluyó una pequeña muestra en agua destilada, y con ayuda de un agitador se homogeneizó la dilución obtenida para separar las partículas y favorecer la observación. Posteriormente, se colocó una gota de la suspensión en una rejilla de cobre para su observación en el microscopio.
Estudio de la transferencia de calor
El fluido de proceso del sistema de colección de energía radiante consistió de agua pura y agua incorporada con partículas. En virtud de la baja concentración de éstas y su nula solubilidad, se aceptó que el fluido se formó en general de agua, por lo que se usaron las propiedades de este fluido como base de trabajo. Se utilizó una ecuación de Antoine (Ecuación 1) (Felder & Rousseau, 2004) para determinar la temperatura de ebullición (T ebull ) a la presión atmosférica (P atm ) del lugar de experimentación (Chapingo, México; P atm = 77 993 Pa), donde P atm se sustituyó en Pa y T ebull se obtuvo en grados Celcius (°C).
Los datos de cambio de temperatura de cada rutina experimental se graficaron en función del tiempo. Entre los distintos sistemas se identificaron los casos donde la temperatura rebasó la T ebull y se determinó el tiempo mínimo para alcanzar un valor cercano, pero menor a ella, y la temperatura correspondiente a ese tiempo en todas las rutinas de evaluación, las cuales se consideraron como tiempo y temperatura de estudio (t est y T est , respectivamente). Para determinar el calor absorbido (Q abs , W) se aplicó un balance de energía con la forma de la Ecuación (2), donde m F es la masa (kg) del fluido de proceso contenido en el sistema de colección de energía (definida en los términos de la Ecuación 3), ( es la densidad (kg·m-3), V es el volumen del fluido (m3), Cp es el calor específico del agua (J·kg-1·°C-1), T ini es la temperatura inicial (°C) y T est es la temperatura de estudio (°C) alcanzada al tiempo de estudio (t est ) definido. Asimismo, se consultaron datos de ( y Cp en la literatura abierta (Geankoplis, 2003) en función de la temperatura, y mediante regresión se ajustaron a modelos con la forma de las Ecuaciones (4) y (5).
Para determinar la temperatura de la superficie interna del sistema tubular de colección de energía (T P ) y el coeficiente de convección térmica interno (h i ), se desarrolló un balance de energía en régimen transitorio. Para ello, se consideraron los sistemas tubulares de colección de energía radiante mostrados en la Figura 1, los cuales se caracterizaron por tener longitud (L, 0.9 m), diámetro interno (D i , 0.0508 m) y masa de fluido de proceso (m F , kg). Se consideró como sistema de estudio al fluido de proceso (agua) contenido en el tubo colector. La Ecuación (6) describe el balance realizado, donde E es el contenido de energía (J), t es el tiempo (s), E e es el flujo de entrada de energía (W) y E s es el flujo de salida de energía (W).
Se reconoció que las lámparas radiantes causaron la elevación de la temperatura de la pared de la tubería hasta un valor T P (°C). En virtud de la alta conductividad térmica del cobre (386 W·m-1·°C-1; Holman, 1986), se aceptó que toda la pared tuvo temperatura homogénea y desde ahí se transfirió calor, por un mecanismo de convección natural, hacia el fluido de proceso, con un flujo que tuvo la magnitud (W) descrita por la Ecuación (7), donde h i es el coeficiente de convección interno (W·m-2·°C-1), A i es el área superficial interna (m2) y T F es la temperatura promedio del fluido de proceso en un tiempo dado (°C).
Por otro lado, en virtud de que la temperatura de la superficie interna de la pared del tubo fue mayor que la del fluido de proceso (T P > T F ), se aceptó que no podía haber pérdida de energía desde el fluido, es decir, que E s = 0. Asimismo, la variación de la energía del mismo fluido de proceso, en la situación donde sólo ocurrió cambio de temperatura sin cambio de fase por evaporación, se describió en la Ecuación (8).
Con estos criterios, la Ecuación (6) se reescribió en la forma de la Ecuación (9), y tras un reordenamiento se obtuvo la Ecuación (10).
A partir de la Ecuación (10) se definió un coeficiente de calefacción (b; s-1) en la forma de la Ecuación (11), con lo cual la Ecuación (10) se simplificó a la forma de la Ecuación (12).
La Ecuación (12) se resolvió con el uso de un factor integrante (F) definido en la Ecuación (13) y el procedimiento descrito en la Ecuación (14) (Kreyszig, Kreyszig, & Norminton, 2011), con lo cual se obtuvo la Ecuación (15). Para evaluar la constante de integración (C), se consideró que al tiempo cero (t = 0) la temperatura del fluido de proceso era T F = T 0 . Con ello, se encontró que C = T 0 - T P , y tras un ordenamiento se obtuvo la Ecuación (16), con el significado de la constante a dado en la Ecuación (17).
Los datos obtenidos de cada rutina experimental se sometieron a una regresión no lineal con apoyo del programa Sigma Plot® (SPSS Inc., 2000) para ajustarlos a un modelo con la forma de la Ecuación (16), donde T 0 (°C), a (°C) y b (s-1) se obtuvieron como constantes de regresión. Para determinar el coeficiente de convección interno (h i ) y la temperatura de la superficie interna de la pared del sistema (T P ), la Ecuación (16) se expresó de manera explícita para el tiempo, en la forma mostrada por la Ecuación (18).
Con la consideración de las Ecuaciones (11) y (17), la Ecuación (18) se expresó también en la forma de la Ecuación (19).
Los parámetros buscados (h i y T P ) se evaluaron con el algoritmo de mínimos cuadrados no lineales (función lsqnonlin.m) disponible en la caja de herramientas de optimización de Matlab® (The Mathworks Inc., 1990). La función se aplicó con la sintaxis descrita en la Ecuación (20) para encontrar los mejores valores de h i y T P , denotados como x(1) y x(2), respectivamente, de forma que la Ecuación (19) reprodujera el comportamiento experimental representado por la Ecuación (18).
La variable x0 definió el conjunto de condiciones iniciales propuestas requeridas por la función lsqnonlin.m para realizar la calibración de x(1) y x(2). La variable lb estableció que los parámetros buscados no podían ser negativos. El corchete vacío indicó que no había límite superior fijado para x(1) y x(2). Adicionalmente, la rutina se desarrolló considerando, como opciones (options), un número máximo de iteraciones de 2 000 y una tolerancia mínima en la función de 1×10-5, de tal forma que el valor óptimo se encontró cuando el cambio relativo de la búsqueda en la dirección del eje de abscisas fue menor a esta referencia.
Análisis de datos
El trabajo se realizó en forma congruente con un arreglo factorial 4×4, bajo en un diseño completamente al azar, donde uno de los factores fue el ángulo de inclinación del sistema colector con cuatro niveles (30, 35, 40 y 45°), y el otro fue el fluido de proceso con cuatro niveles (Ap, y suspensión con Ca, Tc y Nc). Los datos de temperatura alcanzada al tiempo de estudio (T est a t est ), calor absorbido (Q abs ) al t est , temperatura de pared (T P ) y coeficiente de convección térmica interno (h i ) se sometieron a un análisis de varianza y a una prueba de comparación de medias de tratamientos mediante el estadístico de Tukey (P ≤ 0.05). Todos los análisis se realizaron con el programa SAS (SAS Institute Inc., 1999).
Resultados y discusión
Fluidos de proceso
De manera general, las partículas tuvieron una forma esférica (Figura 3), con diámetro promedio de 102.2 ± 20.1 nm las de Ca, 198.4 ± 17.6 nm las de Tc y 160.1 ± 54.1 nm las Nc (Figura 4). Debido a que las dimensiones de las nanopartículas se encuentran en el rango de 1 a 100 nm (Samyn, Barhoum, Öhlund, & Dufresne, 2018), las suspensiones usadas en el presente trabajo no se catalogaron como nanofluidos.
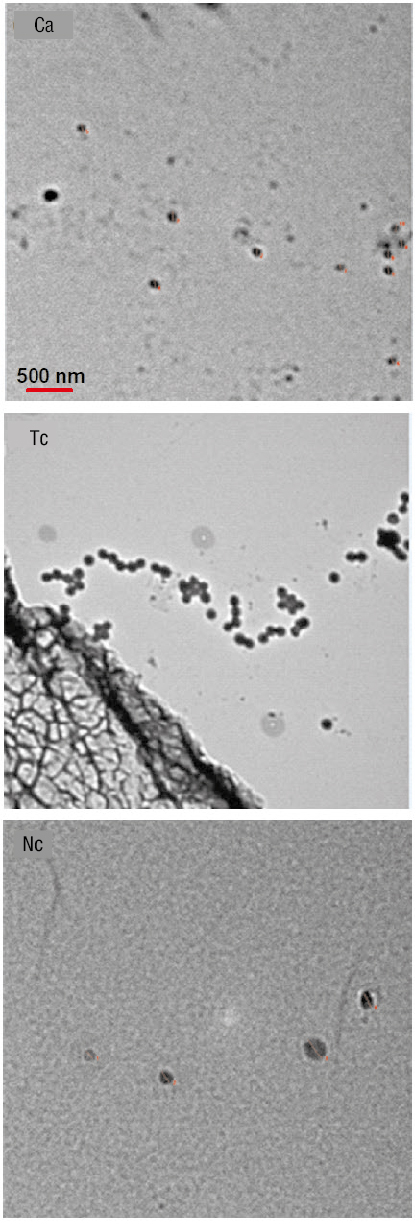
Figura 3 Apariencia de las partículas incorporadas en el fluido de proceso del sistema de colección de energía radiante. Ca = carbón activado; Tc = tinta china; Nc = partículas de cobre.
Variación de la temperatura
La fuente de energía radiante consistió de lámparas de 500 W, con lo cual se simuló la operación en condiciones constantes. Esto fue similar a lo reportado por Wang et al. (2018) y Chen, Munjiza, Zhang, y Wen (2014), quienes realizaron experimentos con una radiación de 300 y 700 W, respectivamente, y obtuvieron un calentamiento uniforme del fluido. Durante la operación, el calentamiento del fluido de proceso ocurrió de forma rápida al inicio, pero con tasa más lenta al paso del tiempo en la mayoría de las rutinas experimentales (Figura 5). Este comportamiento era esperado y fue congruente con un proceso de calentamiento de un material que almacena energía calorífica en régimen transitorio (Valle-Guadarrama, Hernández-Álvarez, & Covarrubias-Gutiérrez, 2007). El calor recibido por el fluido de proceso proviene de la superficie metálica interna del contenedor tubular, y la dimensión del flujo energético es función de la magnitud del gradiente de temperatura entre el fluido y la superficie. A medida que incrementa la temperatura del fluido, el gradiente de temperatura se reduce, lo que causa que el flujo de calor ocurra a menor velocidad y ocasiona que el cambio de temperatura también ocurra a menor tasa (Holman, 1986).
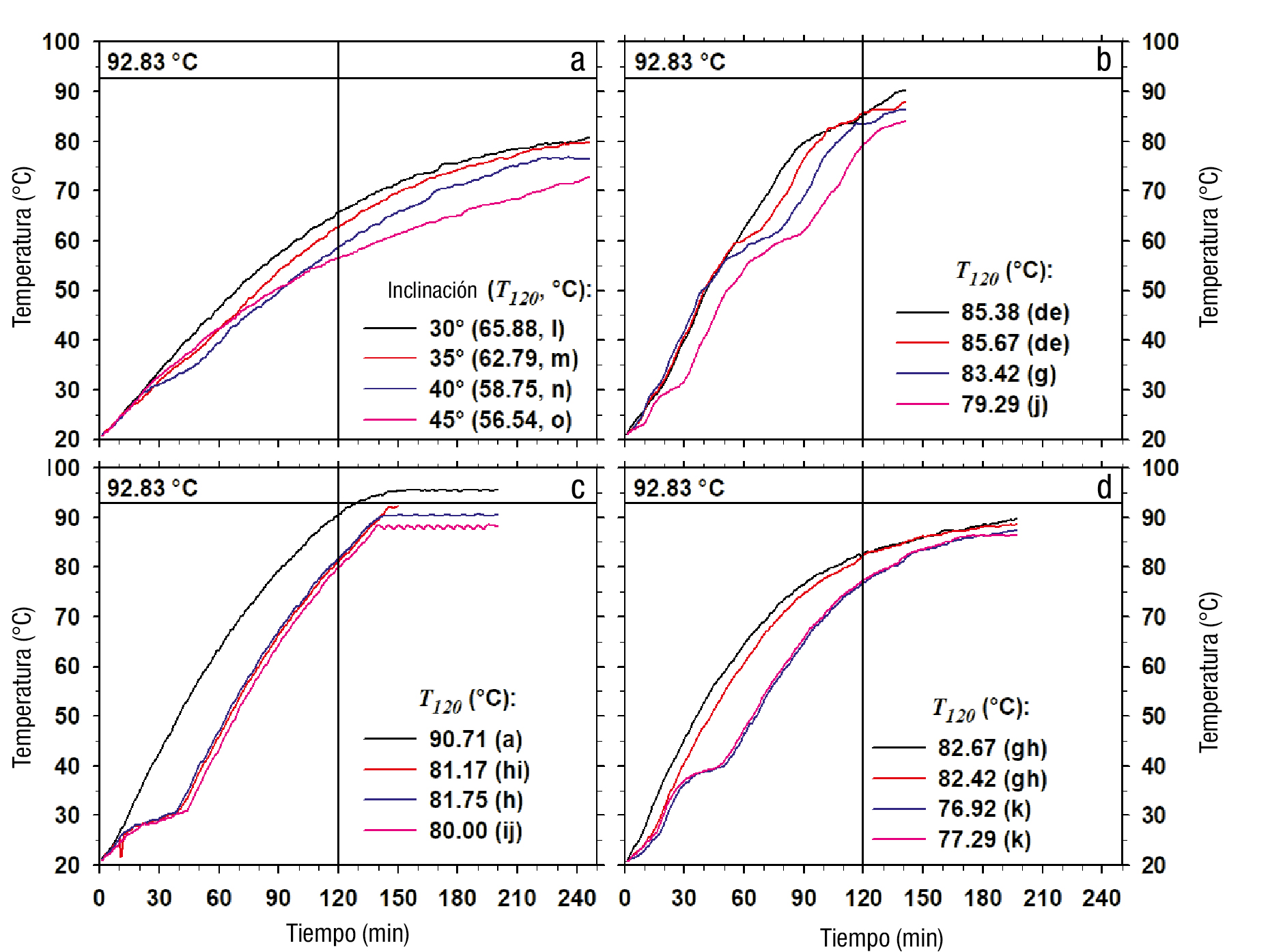
Figura 5 Variación de la temperatura en función del tiempo del fluido de proceso formado por agua pura (a) e incorporada con carbón activado (b), tinta china (c) y partículas de cobre (d). T 120 = temperatura alcanzada después de 120 min de calentamiento. La constante 92.83 °C corresponde a la temperatura de ebullición del agua a 77 993 Pa. Medias iguales asociadas con T 120 no difieren estadísticamente (Tukey, P ≤ 0.05).
A partir de la Ecuación (1), la temperatura de ebullición del agua pura a la presión atmosférica del lugar de experimentación (77 993 Pa; Chapingo, México) es de 92.83 °C. Entre los distintos sistemas, el que alcanzó esta condición en menor tiempo correspondió al que usó agua incorporada con tinta china como fluido de proceso y un ángulo de inclinación de 30°, lo cual ocurrió a los 128 min de exposición a la radiación térmica (Figura 5). Con base en lo anterior, se consideró el tiempo de 120 min como tiempo de estudio de proceso (t est = t 120 ) para evaluar el cambio de temperatura en una condición sin cambio de fase.
La temperatura alcanzada a los 120 min (T 120 ) se afectó tanto por el tipo de fluido de proceso, como por la inclinación del colector, e incluso hubo interacción significativa entre ambos factores de variación (Cuadro 1). A los 120 min de operación, todos los sistemas que usaron suspensiones de partículas presentaron temperaturas promedio que se ubicaron entre 79 y 84 °C, las cuales fueron significativamente mayores (P ≤ 0.05) a la que se registró, en promedio, cuando se usó Ap (61 °C). El análisis de efectos mayores mostró que los sistemas que usaron Ca y Tc causaron la mayor temperatura a los 120 min de operación, sin diferencia significativa (P > 0.05) entre ellos, seguido por el tratamiento con Nc y, finalmente, el sistema con Ap (Figura 5, Cuadro 2).
Cuadro 1 Valores percentiles de la distribución de Fisher (F 0.05 ) y valores de F correspondientes al análisis de varianza de la evaluación de la operación del colector parabólico compuesto (CPC) afectado por el tipo de fluido de proceso y el ángulo de inclinación.
| Variable | Factor de variación | Error | CV (%) | ||
|---|---|---|---|---|---|
| Fluido (F) | Inclina (I) | F×I | |||
| gl | 3 | 3 | 9 | 32 | --.-- |
| F 0.05 | 2.9011 | 2.9011 | 2.1888 | --.-- | --.-- |
| Variables de operación del colector | |||||
| T 120 | 5 410.10* | 547.01* | 50.99* | --.-- | 0.6584 |
| Q abs | 5 796.72* | 589.60* | 5378* | --.-- | 0.8535 |
| T P | 1 169.47* | 26.55* | 50.30* | --.-- | 1.3540 |
| h i | 165.60* | 124.06* | 53.45* | --.-- | 4.7641 |
Fluido = factor de variación dado por el tipo de fluido de proceso; Inclinación = factor de variación dado por la inclinación del colector; F×I = interacción entre los factores tipo de fluido e inclinación; gl = grados de libertad; CV = coeficiente de variación; T 120 = temperatura a los 120 min de operación; Q abs = calor absorbido a los 120 min de operación; T P = temperatura de pared; h i = coeficiente de convección térmica; * = indica que al menos un nivel dentro del factor de variación produjo un efecto diferente en relación con el resto (P ≤ 0.05).
Cuadro 2 Comparación de medias de la operación del colector parabólico compuesto afectada por el tipo de fluido de proceso y el ángulo de inclinación del sistema.
| FV | T 120 (°C) | Q abs (W) | T P (°C) | h i (W·m-2·°C-1) |
|---|---|---|---|---|
| Tipo de fluido | ||||
| Ap | 60.9896 cz (1.0902) | 41.6183 c (1.1055) | 77.5345 c (1.5558) | 12.5197 b (0.4868) |
| Ca | 83.4375 a (0.7743) | 64.1055 a (0.7858) | 92.2767 b (0.9159) | 15.7617 a (0.5378) |
| Tc | 83.4063 a (1.2970) | 64.1564 a (1.2890) | 107.8120 a (1.5805) | 10.6126 c (0.9308) |
| Nc | 79.8542 b (0.8202) | 60.8583 b (0.8337) | 92.3272 b (0.9735) | 15.1566 a (1.1776) |
| DMSH | 0.5602 | 0.5440 | 1.3852 | 0.7121 |
| Inclinación del colector | ||||
| 30° | 81.1563 a (2.8016) | 61.9615 a (2.7978) | 93.6484 b (2.2819) | 16.4855 a (0.8042) |
| 35° | 78.0104 b (2.6987) | 58.7783 b (2.7321) | 94.8894 a (3.6290) | 13.3644 b (1.1020) |
| 40° | 75.2083 c (2.9564) | 55.9543 c (2.9768) | 93.0261 a (3.2262) | 12.1469 c (0.9307) |
| 45° | 73.3125 d (2.9362) | 54.0444d (2.9549) | 90.8985 b (4.3192) | 12.0539 c (0.6658) |
| DMSH | 0.5602 | 0.5446 | 1.3852 | 0.7121 |
FV = factor de variación; T 120 = temperatura a los 120 min de operación; Qabs = calor absorbido a 120 min de operación; T P = temperatura de pared; h i = coeficiente de convección térmica; Ap = agua pura; Ca = agua con carbón activado; Tc = agua con tinta china; Nc = agua con partículas de cobre; DMSH = diferencia mínima significativa honesta. zMedias con letras iguales dentro de cada columna no difieren estadísticamente (Tukey, P ≤ 0.05). Los valores entre paréntesis representan errores estándar.
El uso de partículas en el fluido de proceso en sistemas de colecta de energía radiante ha sido reportado antes (Fang et al., 2013; Neumann et al., 2013; Ni et al., 2015), y se ha demostrado que su presencia, incluso en bajas concentraciones, favorece la transferencia de calor hacia el fluido de proceso. Al respecto, Wang et al. (2018) reportaron el uso de nanopartículas en concentración de 0.05 % de la masa total del fluido de trabajo y explicaron que alrededor de cada partícula se genera un microambiente de mayor retención de energía que favorece la incorporación de ésta al fluido. Por otro lado, a mayor ángulo de exposición a la fuente de energía se tuvo menor temperatura en el fluido de proceso al cumplirse 120 min de operación y transitó, en promedio, de 81.2 °C con 30° a 73.3 °C con 45° (Cuadro 2). Esto sugirió que para favorecer la colecta de energía radiante es recomendable utilizar ángulos pequeños de exposición a la fuente energética.
Los sistemas de colección de energía radiante normalmente se instalan con cierta inclinación, y la determinación del ángulo es un aspecto necesario para optimizar la operación (Tamimi, 2011). En un CPC como el evaluado en el presente trabajo, el uso de inclinación es un rasgo necesario, pues la alimentación de fluido ocurre por la parte superior (Figura 1), con lo cual la menor temperatura y, por tanto, la mayor densidad ocurren en esa región. Con la inclinación se produce un efecto de termosifón que induce convección natural y mejor distribución del calor transferido en todo el fluido. Aunque los resultados sugieren que con ángulos muy pequeños, e incluso con ausencia de inclinación, se puede esperar una mejor colección de energía, ello puede reducir el efecto de la gravedad en la homogeneización de la temperatura, al dificultar el efecto de termosifón. Por esta razón, en el presente trabajo se consideró adecuado evaluar el sistema a partir de 30° de inclinación.
El análisis comparativo de medias de tratamientos individuales mostró que el caso con Tc en el fluido, con ángulo de inclinación de 30°, presentó la mayor temperatura a los 120 min de operación (90.71 °C), seguido del que usó Ca, con ángulo de 30° (85.38 °C) o 35° (85.67 °C), y luego el que usó Nc, también con 30° (82.67 °C) o 35° (82.42 °C). En cada uno de estos casos, con mayor inclinación se tuvo una pérdida rápida de desempeño. Finalmente, el peor funcionamiento se obtuvo con agua pura, donde la temperatura alcanzada a los 120 min varió de 65.88 °C con 30° de inclinación a 56.54 °C con 45° (Figura 6A).
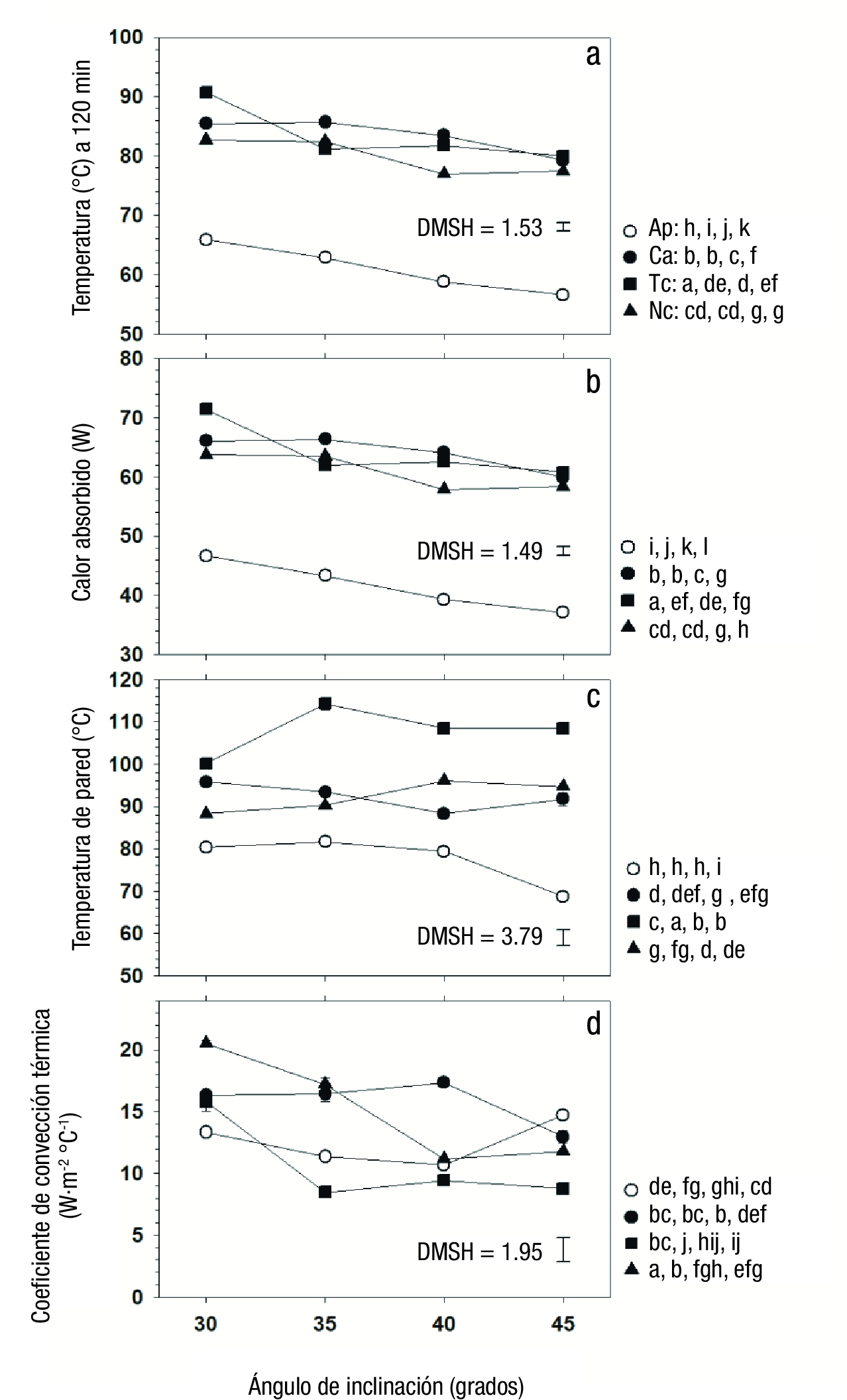
Figura 6 a) Variación de la temperatura alcanzada a 120 min de operación (T 120 ), b) calor absorbido (Q abs ) hasta esa condición, c) temperatura de pared (Tp) y d) coeficiente de convección térmica (hi); todos afectados por el ángulo de inclinación del equipo. Ap, Ca, Tc y Nc representan agua pura y fluido de proceso con carbón activado, tinta china y partículas de cobre, respectivamente. DMSH = diferencia mínima significativa honesta. Medias iguales en cada condición no difieren estadísticamente (Tukey, P ≤ 0.05).
Calor absorbido
El comportamiento del calor absorbido (Q abs , W) fue similar al que se registró en la temperatura alcanzada a los 120 min (T 120 ). Lo anterior debido a que el cálculo de Q abs se realizó con la Ecuación (2), donde la concentración de partículas fue de sólo 0.05 %, por lo que la masa (m F ), que constituyó el fluido de proceso, no varió y la única variable que cambió en estos casos fue la temperatura de estudio (T est = T 120 ), lo cual causó que el comportamiento mostrado por la Figura 6B fuera semejante al mostrado por la Figura 6A. El mayor valor de Q abs ocurrió con Ca y Tc, sin diferencia significativa entre estos casos (P > 0.05), seguido por Nc. La velocidad de transferencia de calor hacia el fluido de proceso fue superior con Ca, Tc y Nc, en 54.03, 54.15 y 46.23 %, respectivamente (Cuadro 2), en comparación con el Ap, lo cual indicó que la incorporación de partículas mejoró significativamente el desempeño del CPC.
En forma similar a lo que ocurrió con T 120 , el Q abs por el fluido de proceso se redujo en forma significativa (P ≤ 0.05) a medida que el ángulo de inclinación se incrementó (Cuadro 2), con diferencia de 12.78 % entre la operación a 30° y 45°. Este comportamiento fue observado en todos los fluidos de proceso, donde los mayores valores de Q abs se registraron con 30° y los menores con 45° de inclinación (Figura 6B).
Temperatura de superficie de pared
La temperatura alcanzada en la superficie interna de la pared del tubo que contuvo el fluido de proceso (T P ) se afectó por los dos factores de variación de manera significativa, y la interacción entre ambos resultó también significativa (Cuadro 1). El análisis de efectos mayores mostró que la mayor temperatura promedio de pared (P ≤ 0.05) se registró en el sistema que usó Tc, luego el que incorporó Ca y Nc, sin diferencia entre éstos, y finalmente el que usó Ap. Dado que las mayores temperaturas de líquido y los mayores valores de calor absorbido se registraron con los menores ángulos de inclinación, se esperaba que la mayor temperatura en la superficie sólida hubiera correspondido a los menores ángulos; sin embargo, aunque hubo diferencia causada por los distintos ángulos de inclinación, no se identificó una tendencia clara.
Por otro lado, hubo interacción significativa entre los factores de variación, y el análisis de cada fluido en particular mostró que se formaron tres grupos. Uno de ellos estuvo integrado por Tc, donde se registraron los mayores valores de T P (Figura 6C). El segundo grupo estuvo formado por Ca y Nc, donde se tuvo comportamiento similar en todos los ángulos. Finalmente, el tercer grupo incluyó sólo al Ap, cuyo valor de T P fue muy inferior (P ≤ 0.05) al registrado en los sistemas que incorporaron alguna partícula en suspensión, y el valor se redujo incluso más con el mayor ángulo de inclinación, lo que confirmó que el uso de partículas permite una mejoría en el funcionamiento del CPC.
Coeficiente de convección térmica interno
La transferencia de calor desde la superficie interna del tubo contenedor hacia el fluido de proceso ocurrió por un mecanismo de convección natural. El coeficiente de convección térmica (h i ) asociado con este intercambio de calor varió entre 10.61 y 15.76 W·m-2·°C-1. El coeficiente h i representa el flujo de calor transferido por unidad de área y unidad de gradiente de temperatura (Ecuación 7; Holman, 1986). El valor de h i se afectó por el tipo de fluido (Cuadro 1), y fue mayor en el sistema que usó Nc y Ca, luego por el sistema basado en Ap y, finalmente, por el que usó Tc. Dado que en todos los casos el área de transferencia de calor fue la misma, los resultados mostraron que los sistemas basados en Tc permiten menor transferencia de calor por cada grado de diferencia de temperatura entre el fluido y la superficie sólida del sistema. No obstante, los datos de calor absorbido mostraron que incluso con esta característica, el sistema basado en Tc, con ángulo de inclinación de 30°, representa la mejor alternativa de operación.
Por otro lado, se encontró que con menor ángulo de inclinación los valores del coeficiente h i fueron mayores (Cuadro 2), pero la interacción entre el tipo de fluido y el ángulo de inclinación como factores de variación fue significativa (Cuadro 1). El análisis de cada fluido en particular mostró que los sistemas que usaron Tc y Nc tuvieron reducción clara de h i con el aumento del ángulo de inclinación, pero en los otros dos sistemas este coeficiente se mantuvo sin cambios importantes (Figura 6D).
El sistema de colección de energía radiante evaluado se basó en el uso de fluido de trabajo mantenido en forma estacionaria dentro del tubo colector, por lo cual, la transferencia de calor desde la superficie sólida interna al fluido correspondió a una convección natural. En tal sentido, los valores obtenidos para el coeficiente h i fueron similares a los reportados en la literatura para distintas geometrías que desarrollan transferencia de calor por convección natural, donde los valores fluctúan entre 5 y 25 W·m-2·°C-1 (Holman, 1986).
Validación de utilidad
Se realizaron mediciones físicas de la temperatura de la pared del tubo contenedor del fluido de proceso con un sensor infrarrojo de temperatura de superficie (Multímetro EXTECH™, EX810, EUA), hasta alcanzar una condición de estabilización en el tiempo. Los datos experimentales se compararon con aquellos estimados con la rutina de modelado a través de una representación uno a uno (Figura 7). Los pares de datos medidos-estimados se sometieron a una rutina de regresión lineal, de donde se obtuvo un coeficiente de determinación (R 2) igual a 0.8083, lo que indicó que la estimación hecha mediante la rutina lsqnonlin.m de Matlab® logró predecir los datos de la temperatura de pared del sistema en un 80.8 %. En particular, los datos correspondientes a Ap mostraron tendencia a ser sobre-estimados, pero en el resto no se observó una tendencia clara de sub- o sobre-estimación. En general, se consideró aceptable la estimación de parámetros térmicos hechos con el modelo.
Eficiencia de operación
Para evaluar el sistema de colección de energía radiante se utilizaron tres lámparas de 500 W colocadas a una distancia de 40 cm de la parte superior de las involutas del sistema con inclinación de 30° (Figura 2). El área de incidencia de energía radiante fue de 1.6 m2, lo cual generó un flux de energía disponible de 937.5 W·m-2; mientras que el área de las tres involutas fue de 0.3343 m2, lo que indicó que la incidencia de energía radiante sobre ellas fue de 313.41 W. Lee, Park, Walsh, y Xu (2012) encontraron que incluso con una concentración baja de nanopartículas (0.05 % en volumen), el nanofluido alcanzó una eficiencia de colección de energía de hasta 70 % sin ningún grado de inclinación. Con base en los datos de calor absorbido reportados en la Figura 6 para la inclinación de 30°, las eficiencias de aprovechamiento del calor radiante fueron de 68.4 % para la Tc, 63.2 % para el Ca, 61.0 % para las Nc y 44.6 % para el Ap, lo que confirmó que la incorporación de partículas en el fluido receptor incrementó significativamente la eficiencia del CPC.
Conclusiones
El incremento del ángulo de inclinación causó una reducción de la capacidad de colección de energía radiante del CPC. La incorporación de partículas al fluido de proceso mejoró significativamente el desempeño del CPC, en comparación con el sistema en el cual se utilizó agua pura como fluido. Las mejores características de operación se obtuvieron con la incorporación de tinta china, seguido del uso de carbón activado, los cuales constituyen alternativas adecuadas para atender el manejo de un CPC.
Agradecimientos
Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (CONACyT), México, por el apoyo económico otorgado para la presente investigación.
REFERENCIAS
Bello-Bello, J. J., Chavez-Santoscoy, R. A., Lecona-Guzmán, C. A., Bogdanchikova, N., Salinas-Ruíz, J., Gómez-Merino, F. C., & Pestryakov, A. (2017). Hormetic response by silver nanoparticles on in vitro multiplication of sugarcane (Saccharum spp. Cv. Mex 69-290) using a temporary immersion system. Dose-Response: An International Journal, 2017, 1-9. doi: 10.1177/1559325817744945 [ Links ]
Chen, X., Munjiza, A., Zhang, K., & Wen, D. (2014). Molecular dynamics simulation of heat transfer from a gold nanoparticle to a water pool. The Journal of Physical Chemistry C, 118(2), 1285-1293. doi: 10.1021/jp410054j [ Links ]
Debernardi-de la Vequia, H., Ortiz-Laurel, H., & Rosas-Calleja, D. (2016). Energía disponible a partir de biomasa de residuos de caña de azúcar (Saccharum spp.). Agroproductividad, 9(7), 68-73. Retrieved from http://revista-agroproductividad.org/index.php/agroproductividad/article/view/792 [ Links ]
Elimelech, M., & Phillip, W. A. (2011). The future of sea water desalination: energy, technology, and the environment. Science, 333(6043), 712-717. doi: 10.1126/science.1200488 [ Links ]
Fang, Z., Zhen, Y. R., Neumann, O., Polman, A., García-de Abajo, F. J., Nordlander, P., & Halas, N. J. (2013). Evolution of light-induced vapor generation at a liquid-immersed metallic nanoparticle. Nano Letters, 13(4), 1736-1742. doi: 10.1021/nl4003238 [ Links ]
Felder, R. M., & Rousseau, R. W. (2004). Elementary principles of chemical processes. USA: John Wiley & Sons, Inc. [ Links ]
Geankoplis, C. J. (2003). Transport processes and separation process principles (includes unit operations). New Jersey: Prentice Hall. [ Links ]
Holman, J. P. (1986). Heat transfer. New York: McGraw-Hill Book Company Incorporation. [ Links ]
Kreyszig, E., Kreyszig, H., & Norminton, E. J. (2011). Advanced engineering mathematics. New Jersey: John Wiley & Sons, Inc. [ Links ]
Lee, B. J., Park, K., Walsh, T., & Xu, L. (2012). Radiative heat transfer analysis in plasmonic nanofluids for direct solar thermal absorption. Journal of Solar Energy Engineering, 134(2), 021009-021009-6. doi: 10.1115/1.4005756 [ Links ]
Lewis, N. S. (2007). Toward cost-effective solar energy use. Science , 315(5813), 798-801. doi: 10.1126/science.1137014 [ Links ]
Neumann, O., Urban, A. S., Day, J., Lal, S., Nordlander, P., & Halas, N. J. (2013). Solar vapor generation enabled by nanoparticles. ACS Nano, 7(1), 42-49. doi: 10.1021/nn304948h [ Links ]
Ni, G., Miljkovic, N., Ghasemi, H., Huang, X., Boriskina, S. V., Lin, C. T., Wang, J., Xu, Y., Rahman, M. M., Zhang, T., & Chen, G. (2015). Volumetric solar heating of nano fluids for direct vapor generation. Nano Energy, 17, 290-301. doi: 10.1016/j.nanoen.2015.08.021 [ Links ]
Panwar, N. L., Kaushik, S. C., & Kothari, S. (2011). Role of renewable energy sources in environmental protection: A review. Renewable and Sustainable Energy Reviews, 15(3), 1513-1524. doi: 10.1016/j.rser.2010.11.037 [ Links ]
Samyn, P., Barhoum, A., Öhlund, T., & Dufresne, A. (2018). Review: nanoparticles and nanostructured materials in papermaking. Journal of Materials Science , 53, 146-184. doi: 10.1007/s10853-017-1525-4 [ Links ]
SAS Institute, Inc. (1999). SAS/STAT® User’s guide , version 8. Cary, USA: Author. [ Links ]
SPSS Inc. (2000). SigmaPlot® 2000 User’s guide. Chicago: Author. [ Links ]
Steinfeld, A. (2005). Solar thermochemical production of hydrogen - a review. Solar Energy, 78(5), 603-615. doi: 10.1016/j.solener.2003.12.012 [ Links ]
Tamimi, A. I. (2011). Modeling of optimum inclination angles of solar systems for Amman, Jordan. Journal of Renewable and Sustainable Energy, 3, 043109, 1-9. doi: 10.1063/1.3610974 [ Links ]
The Mathworks, Inc. (1990). Optimization Toolbox™ 4, user’s guide. Natick, Massachusetts, USA: Author. [ Links ]
Valle-Guadarrama, S., Hernández-Álvarez, R. L., & Covarrubias-Gutiérrez, I. (2007). Modeling of the heating and cooling internal rates in fruits. Case: Mexican lime. Revista Fitotecnia Mexicana, 30(1), 61-68. Retrieved from https://www.revistafitotecniamexicana.org/documentos/30-1/10r.pdf [ Links ]
Wang, H., Yang, W., Cheng, L., Guan, C., & Yan, H. (2018). Chinese ink: high performance nanofluids for solar energy. Solar Energy Materials and Solar Cells, 176, 374-380. doi: 10.1016/j.solmat.2017.10.023 [ Links ]
Xu, G., Song, G., Zhu, X., Gao, W., Li, H., & Quan, Y. (2015). Performance evaluation of a direct vapor generation supercritical ORC system driven by linear Fresnel reflector solar concentrator. Applied Thermal Engineering, 80, 196-204. doi: 10.1016/j.applthermaleng.2014.12.071 [ Links ]
Recibido: 27 de Febrero de 2019; Aprobado: 12 de Marzo de 2020











 texto en
texto en 





