Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Chapingo serie ciencias forestales y del ambiente
versión On-line ISSN 2007-4018versión impresa ISSN 2007-3828
Rev. Chapingo ser. cienc. for. ambient vol.23 no.1 Chapingo ene./abr. 2017
https://doi.org/10.5154/r.rchscfa.2015.11.052
Artículos
Metanálisis para el volumen de Pinus sylvestris en Europa
1Democritus University of Thrace, Department of Forestry and Management of the Environment and Natural Resources. Pandazidou 193, 68200, Orestiada, Greece.
Las revisiones sistemáticas son herramientas importantes para la investigación de literatura objetiva, composición y análisis crítico de los resultados de estudios variantes, con una contribución excelente para aclarar temas y buscar nuevas direcciones de investigación. Este estudio tiene como objetivo la revisión sistemática de estudios independientes para la estimación del volumen de pino silvestre (Pinus sylvestris) en Europa. Para ello, se realizó un metanálisis de los modelos de estimación de volumen de árboles individuales. En este trabajo se describen las etapas del metanálisis, los métodos estadísticos, los posibles errores derivados y la heterogeneidad que se producen entre los estudios. Los resultados muestran que Italia se distingue claramente por tener volúmenes de árbol individual demasiado pequeños, mientras que Grecia y Suecia presentan grandes volúmenes. Existe una gran heterogeneidad entre los estudios, debido probablemente a las condiciones distintas de competencia suscitadas en los rodales de diferentes países de Europa, pero sin clima distinto. Más estudios podrían servir en el caso de Italia; en el caso de Grecia, un estudio con una muestra de mayor tamaño podría contribuir para fomentar la investigación.
Palabras clave: Productividad de los bosques; volumen de árbol individual; pino silvestre; revisión sistemática.
Systematic reviews are important tools for objective literature research, composition and critical analysis of variant studies results, with an excellent contribution in clarifying issues and searching for new research directions. This study aims the systematic review of independent studies of volume estimation for Scots pine (Pinus sylvestris) in Europe. A meta-analysis of individual tree volume estimation models was performed. The stages of meta-analysis, statistical methods, possible errors arising, and heterogeneity that occur among studies are described in detail. Results showed that Italy is clearly distinguished (volumes are too small), Greece and Sweden present large volumes, and there is great heterogeneity among studies, probably due to different competition conditions created in stands in different countries of Europe, not different climate. More research could be useful in Italy, and in Greece, a study with a larger sample size could contribute to the promotion of research.
Keywords: Forest productivity; individual tree volume; scots pine; systematic review.
Introducción
Una de las coníferas de mayor distribución es el pino silvestre (Pinus sylvestris L.), el cual se encuentra a lo largo de vastas áreas de Asia y Europa. Una amplia superficie en esta área de distribución natural se encuentra cubierta por dicho árbol, y esto ayuda a reflejar la variabilidad en la productividad, que a menudo es mostrada por esta especie (Boratynski, 1991).
El pino silvestre se extiende al norte, a lo largo de la costa noruega a 70° N, y al sur, en la Sierra Nevada de España a 37° N. La franja de longitud se extiende sobre Siberia cubriendo la mayor parte de Europa hasta los 138° E. Los rodales de pino silvestre pueden distribuirse de forma desigual, lo que realmente caracteriza a la mayor parte de bosques en Europa. De manera desglosada, la cubierta forestal total es de 65 % en Finlandia (Sevola, 1998), 20 % en los bosques altos en el Reino Unido (Christie & Lines, 1979) y sólo 9 % del área forestal total se encuentra en Francia (Bazire & Gadant, 1991) Pinus sylvestris cubre 0.32 % de los bosques en Grecia (Ministry of Agriculture, 1992). En un estudio comparativo, Christie y Lines (1979) registraron los datos de rendimiento y crecimiento de pinos silvestres en toda Europa y evaluaron la media nacional de los incrementos anuales en Reino Unido, la cual oscilaba de 2+ a 18+ (m3∙ha-1∙yr-1). Como todas estas cifras hacen referencia a las condiciones óptimas de fertilidad a partir del nivel nacional, cualquier diferencia observada puede atribuirse principalmente a los factores climáticos. Como resultado de otros estudios, se pudo obtener una interpretación de las diferencias entre los rasgos estructurales, las respuestas fisiológicas y las diferencias en el crecimiento. Todo esto se hizo con el fin de identificar qué factores clave y limitantes son intraespecíficos, y los ajustes originados por el clima, para el pino silvestre (Mencuccini & Bonosi, 2001; Poyatos et al., 2007); sin embargo, nuestra principal preocupación fue saber cómo la diferencia de latitud y el clima podrían dar lugar a una diferencia en la productividad.
La productividad se calcula comúnmente en términos de volumen; este parámetro, por lo general, se calcula a partir de modelos de regresión de árboles individuales, utilizando el diámetro a la altura del pecho y la altura total como predictores (Van Laar & Akça, 2007). Por lo tanto, con el fin de abordar y responder a la cuestión de la productividad del pino silvestre en Europa, se aplicó un método de metanálisis de los modelos de regresión de estimación del volumen de árboles individuales.
Hoy en día, la tasa de producción y enriquecimiento de conocimiento son muy rápidos. La gran cantidad de publicaciones y el gran volumen de información dificultan la evaluación e implementación de una práctica de investigación basada en la evidencia documentada que, en estas circunstancias, resulta vital para la preservación de la calidad de las publicaciones científicas. Además, es necesario que los autores y editores sigan las instrucciones y métodos específicos con el fin de garantizar la utilidad y validez de la información existente (Borenstein, Hedges, & Higgins 2009).
La realización de un metanálisis se basa en principios científicos y en la formulación de reglas que los investigadores/autores deben seguir para reducir al mínimo los errores que, por definición, existen en cada artículo científico (Borenstein et al., 2009). El objetivo de este estudio fue la aplicación del método de metanálisis en modelos de estimación de volumen de pino silvestre (P. sylvestris), para convertirse en una síntesis cuantitativa de datos provenientes de estudios distintos que tratan el mismo tema, para estimar una puntuación total o global de todos los estudios (efecto combinado) y detectar heterogeneidad entre ellos.
Materiales y métodos
Varios investigadores han propuesto pautas específicas para la realización del metanálisis (Borenstein et al., 2009; Cooper, 2010; Lipsey & Wilson, 2001). Las etapas del metanálisis en este documento se describen a continuación.
Definición del problema - definición del tamaño del efecto
Con el fin de tener una síntesis cuantitativa de los diferentes estudios que estiman el volumen de P. sylvestris, se estandarizó la variable dependiente; es decir, el volumen. En el metanálisis, el tamaño del efecto (TE) es la variable dependiente que estandariza los hallazgos en los estudios de modo que puedan ser comparados directamente. Los metanálisis pueden utilizar diferentes variables de tamaño del efecto. Cada estándar puede ser una variable de tamaño de efecto (por ejemplo, la diferencia de medias estandarizada, el coeficiente de correlación o la relación de probabilidad), ya que la variable es comparable en todos los estudios, representa el tamaño y la dirección de la relación que interesa, y es independiente del tamaño de la muestra. En este estudio, el TE fue el volumen estimado de un árbol con diámetro a la altura del pecho de 41 cm y altura total de 24 m tomado del estudio de Kitikidou, Milios, y Lipiridis (2014). Este estudio se utilizó como referencia, ya que la gran mayoría de los estudios europeos relativos incluyeron las medidas 41 cm y 24 m en sus rangos de diámetro a la altura del pecho (D) y altura total (H), respectivamente. La única conversión que se aplicó en los modelos de estimación de volumen fue la unidad de medida; todos los modelos se convirtieron para calcular el volumen en m3.
Estudios de recuperación
Es fundamental que haya criterios explícitos para la inclusión y exclusión de los estudios que participan en el metanálisis. Existe un dilema metodológico: ¿deben incluirse o no los estudios de baja calidad? Si se es demasiado estricto, entonces se puede limitar la capacidad de generalización. Por otro lado, si se incluyen los estudios simples, entonces la exactitud de las conclusiones puede debilitarse. Por lo tanto, se debe lograr un equilibrio adecuado para el tema de investigación (Borenstein et al., 2009).
Para el metanálisis de estimación de volumen (v) de P. sylvestris en Europa, se recolectaron todos los estudios europeos que describen los modelos de estimación de volumen del árbol individual. Como árbol de referencia, se utilizó un árbol con diámetro a la altura del pecho de 41 cm y altura total de 24 m; todos los estudios europeos incluidos en el metanálisis tuvieron estas medidas. El uso de un árbol de referencia es fundamental, a fin de tener volúmenes comparables. Ocho modelos se incluyeron en el metanálisis, recuperados de Google Scholar <http://scholar.google.com>, para el periodo 1900-2015 (Cuadro 1).
Cuadro 1 Estadística descriptiva de los ocho modelos utilizados en el metanálisis para la estimación del volumen de Pinus sylvestris en Europa.
| Núm. | Estudio | Ecuación | D min (cm) | D max (cm) | H min (m) | H max (m) | Tamaño de la muestra n | Volumen estimado (m3) de un árbol con D = 41 cm y H = 24 m |
| 1 | Laasasenaho (1982) | V = -2.2945 + 2.57025 * LN(D) | 0.9 | 50.6 | 1.5 | 28.3 | 2,050 | 1.007 |
| 2 | Laasasenaho (1982) | V = -5.39417 + 3.4806 * LN (2 + 1.25 *D)-0.039884 * D | 0.9 | 50.6 | 1.5 | 28.3 | 2,050 | 1.006 |
| 3 | Laasasenaho (1982) | V = 0.036089 (D2.01395) (0.99676 D ) (H2.07025) [(H-1.3)-1.07209] | 0.9 | 50.6 | 1.5 | 28.3 | 2,050 | 1.416 |
| 4 | Laasasenaho and Sevola (1971) | V = -2.37912 + 2.62903 * LN(D) + 0.000126 (D2) | 7.0 | 50.0 | 5.0 | 28.0 | 1,291 | 1.007 |
| 5 | Corona and Ferrara (1987) | V = 1.480589 (D1.982459514) (H0.742674501) | 13.0 | 49.0 | 7.0 | 27.5 | 114 | 0.046 |
| 6 | Näslund (1947) | V = 0.1028 (D2) + 0.02705 (D2) H + 0.005215 (D2) H | 5.0 | 49.9 | 3.0 | 32.9 | 4,421 | 1.474 |
| 7 | Näslund (1947) | V = 0.1072 (D2) + 0.02427(D2) H + 0.007315 * D(H2) | 5.0 | 49.9 | 3.0 | 32.9 | 2,390 | 1.332 |
| 8 | Kitikidou et al. (2014) | V = 0.318 (D2) H | 19.0 | 72.0 | 17.0 | 41.0 | 158 | 1.282 |
V: Volumen, D: Diámetro, H: Altura
Análisis del tamaño del efecto
Supóngase que se tiene un conjunto de variables independientes TE que se han transformado o adaptado, de ser necesario, para cada TE para lo que tenemos una varianza ponderada w inversa. El promedio TE es igual a:
el error estándar de la media es:
El intervalo de confianza de 95 % se calcula como limite inferior = TE - 1.96(se
TE
) y limite superior = TE + 1.96(se
TE
); el análisis de homogeneidad verifica si se aplica la hipótesis de que todos los tamaños estiman la población media. Como es de esperar este caso rara vez se aplica, ya que los distintos estudios calculan de manera diferente el TE. Si se calculan los totales
Si el Q calculado es menor que el valor crítico de χ2 con gl y valor P conocidos (por ejemplo, 0.05), no se puede rechazar la hipótesis nula de la prueba de homogeneidad. En este caso, la varianza en todos los tamaños no excede el resultado esperado basado en el error de muestreo. Además de Q, la heterogeneidad se puede controlar con el índice de inconsistencia:
De acuerdo con una clasificación muy ordinaria, la heterogeneidad puede ser denominada como baja si 25 ≤ I2 ≤ 50 %, es moderada si 50 < I2 ≤ 75 %, y si I2 > 75 se considera buena (Higgins, Thompson, Deeks, & Atman, 2003).
Gráficas en el metanálisis
Las gráficas sirven para detectar si existe un error sistemático de publicación (sesgo de publicación). Si la selección de los estudios incluidos en el metanálisis fue parcial según la puntuación, se debe utilizar el gráfico de embudo invertido (o funnel plot) (Egger, Smith, Schneider, & Minder 1997; Sterne & Egger, 2001). El eje horizontal es el tamaño de salida y TE vertical es el tamaño de la muestra, error estándar o variación inversa ponderada, por lo que cada punto de la gráfica representa un estudio. Si no existe error de publicación, la gráfica es simétrica. El gráfico en embudo recibe gran crítica, ya que el tamaño del efecto de un estudio s-s es distinto, debido al “tamaño del estudio” diferente, entonces este gráfico puede ser erróneo (Lau, Ioannidis, Terrin, Schmid, & Olkin, 2006).
Se ha desarrollado un método gráfico llamado diagrama de bosque para detectar la heterogeneidad (Panagiotakos, 2006). En este gráfico, se puede examinar visualmente la superposición de los intervalos de confianza para los estudios individuales en un metanálisis. En un diagrama de bosque típico, los resultados de los estudios están representados por cuadrados, mientras que los extremos de la línea horizontal en cada cuadrado representan los límites del intervalo de confianza para cada estudio. La evaluación general del metanálisis para el estudio de la intensidad de la relación entre los estudios y los intervalos de confianza se coloca en la base del diagrama, con una línea vertical distinta. La línea vertical representa el promedio de TE.
Modelos de efectos fijos y aleatorios
Si se toma en cuenta que una variación excesiva en tamaños de resultado se obtuvo de las diferencias aleatorias entre los estudios (fuentes que no se pueden identificar o contar), se debe utilizar un modelo de efectos fijos (Mantel & Haesnszel, 1959).
El modelo de efectos fijos pondera cada estudio con la inversa de la varianza muestral:
En un modelo de efectos aleatorios (DerSimonian & Laird, 1986) se encontró que los tamaños del efecto provienen de un mayor número de tamaños del efecto (incluyendo encuestas) de manera aleatoria. El modelo de efectos aleatorios, que pondera cada estudio con la inversa de la varianza muestral y una constante que representa la variación de los efectos en la población, es:
donde
El componente de la varianza de efectos aleatorios se basa en Q; el tipo de cálculo Q en el modelo de efectos aleatorios es:
La mayor diferencia que sobresale al comparar los resultados de los modelos de efectos fijos y aleatorios son los niveles de significación e intervalos de confianza. Los intervalos de confianza en los modelos de efectos aleatorios son más grandes, mientras que los efectos que fueron significativos en el modelo de efectos fijos pueden no ser significativos en el modelo de efectos aleatorios. Si el tamaño de la muestra se asocia con el tamaño del efecto, entonces la media de TE diferirá entre los dos modelos.
Resultados y discusión
En el Cuadro 2 se muestran las estadísticas del metanálisis. Los ocho modelos que estiman el volumen de P. sylvestris (Cuadro 1) fueron significativamente heterogéneos, ya que el Q estimado fue mayor que el valor crítico de I2, si se acepta que las diferencias entre los estudios son aleatorias y que no se pueden medir. En este caso al aplicar el modelo de efectos fijos, la heterogeneidad es grande (I2 = 99.8 %). Por el contrario, si se acepta que los ocho modelos fueron seleccionados al azar, a partir de una serie de estudios; es decir, aplicando el modelo de efectos aleatorios, la heterogeneidad es nula (5.259 < 14.067 y I2 = 0). Tomando en cuenta que hemos hecho el metanálisis de todos los estudios disponibles que cumplen con nuestro criterio (los modelos incluyen árbol con diámetro a la altura del pecho de 41 cm y altura total de 24 m). En este punto, hay que señalar que la comparación de los estudios se refiere a sus rangos D, H y no a los pares D, H específicos de valores de 41 cm y 24 m. El tamaño del efecto promedio parece no variar entre los modelos de efectos fijos (1.025) y efectos aleatorios (1.071), lo que significa que el tamaño de la muestra parece no estar altamente correlacionado con el tamaño del efecto.
Cuadro 2 Estadísticas del metanálisis de los ocho modelos para la estimación del volumen de Pinus sylvestris.
| Estadísticas | Modelo de efectos fijos | Modelo de efectos aleatorios | Número de estudios (k) | Grados de libertad | Valor crítico χ2 (valor P) |
| Q | 3,353.167 | 5.226 | 8 | 7 | 14.067 |
| I2 | 99.791 | 0.000 | |||
| 𝐸𝑆 / 𝑇𝐸 | 1.025 | 1.071 | |||
| 𝑠𝑒 𝐸𝑆 / ( 𝑠𝑒 𝑇𝐸 ) | 0.008 | 0.187 | |||
| Intervalo de confianza (Límite inferior-superior) | 1.008-1.042 | 0.705-1.437 |
Q: Estadístico de Cochran, I2: índice de inconsistencia, EQ \x \to(TE) : media del tamaño del efecto, se EQ \x \to(TE) : error estándar de la media del TE
En el gráfico de embudo (Figura 1) parece existir un sesgo de publicación (los puntos no forman un triángulo invertido). Con color gris se simbolizó el estudio en Italia (Corona & Ferrara, 1987), verde para Finlandia (Laasasenaho, 1982; Laasasenaho & Sevola, 1971), café para Suecia (Näslund, 1947) y azul para Grecia (Kitikidou et al, 2014). Si se observa, el estudio número 5 realizado en Italia sale fuera del triángulo; es decir, tiene el tamaño más pequeño de la muestra, sólo 114 árboles (Cuadro 1). Esto puede crear un gráfico en embudo erróneo con respecto al sesgo de publicación; es decir, los puntos no forman un triángulo invertido, debido al tamaño pequeño de la muestra de un estudio y no debido a la selección sesgada de los estudios.

Figura 1 Gráfico en embudo de los ocho modelos que formaron parte en el metanálisis para la estimación del volumen de Pinus sylvestris en Europa. Los números 1 a 4 representan a los estudios realizados en Finlandia, el 5 corresponde a Italia, el 6 y 7 a Suecia y el 8 a Grecia.
En el diagrama de bosque (Figura 2), la línea central representa el promedio de los estudios; es decir, el volumen estimado promedio de ocho modelos con diámetro a la altura del pecho del árbol de 41 cm y altura total de 24 m. Al igual que en la Figura 1, con color gris se representa el estudio en Italia (Corona & Ferrara, 1987), verde para Finlandia (Laasasenaho, 1982; Laasasenaho & Sevola, 1971), café para Suecia (Näslund, 1947) y azul para Grecia (Kitikidou et al., 2014). Existe una clara tendencia para volúmenes grandes (muy por encima del promedio) en Grecia y Suecia, mientras que por debajo del promedio parecen estar los volúmenes de los árboles de P. sylvestris en Finlandia. En Italia se encuentran claramente los volúmenes más pequeños en comparación con el resto de Europa. Además, al observar los límites de los errores de la línea horizontal, se encontró que el estudio realizado en Grecia muestra un intervalo de confianza bueno, el cual se debe al error estándar y, por lo tanto, al tamaño pequeño de la muestra (165 árboles), en relación con otros estudios.
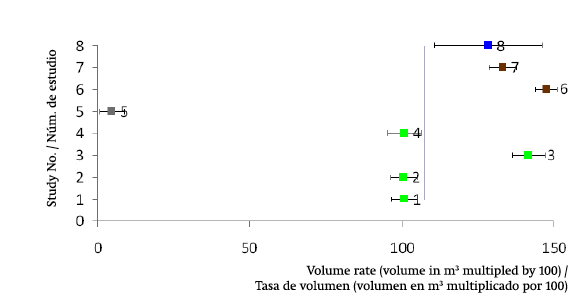
Figura 2 Diagrama de bosque de los ocho modelos que se emplearon en el metanálisis para la estimación del volumen de Pinus sylvestris en Europa. Los números 1 a 4 representan a los estudios realizados en Finlandia, el 5 corresponde a Italia, el 6 y 7 a Suecia y el 8 a Grecia.
La revisión sistemática y el metanálisis ofrecen una nueva evaluación de los datos de la investigación que se refiere a una cuestión científica particular que surgió de diversos estudios. La aplicación del metanálisis en el sector forestal puede ayudar en lo siguiente (Kitikidou, Milios, Stampoulidis, & Papageorgiou, 2013; Papakosta, Kitikidou, Bakaloudis, & Vlachos, 2014): permite la síntesis de un gran número de resultados de investigaciones forestales; puede resaltar diferencias en la investigación bibliográfica, proporcionando una base sólida para la próxima generación de investigación en un tema forestal; demuestra la importancia de la repetición de una investigación; y facilita la generalización de los conocimientos adquiridos con las encuestas de corto alcance.
En el metanálisis llevado a cabo en esta investigación, al usar modelos de estimación de volumen para pino silvestre (P. sylvestris), encontramos que:
La síntesis cuantitativa de los datos, a partir de diferentes estudios, mostró que Italia necesita mayor investigación. El estudio de Corona y Ferrara (1987) no es suficiente para una conclusión clara (probablemente el tamaño de la muestra de este estudio es pequeño).
Mediante el cálculo de un total, resultado del resumen de todos los estudios (efecto agrupado), se encontró un volumen promedio del árbol P. sylvestris con diámetro a la altura del pecho de 41 cm y altura total de 24 m igual a 1.072 m3, mientras que un árbol con estas dimensiones en el estudio de Kitikidou et al. (2014) tuvo un volumen de 1.153 m3. No obstante, el intervalo de confianza debe ser señalado para el estudio en Grecia. Esto probablemente es el resultado de la influencia de dos factores; en primer lugar, condiciones de crecimiento diferentes, conduciendo a los factores de manera distinta (Kitikidou et al, 2014); en segundo lugar, el tamaño pequeño de la muestra (158 árboles).
En cuanto a la heterogeneidad entre los estudios, si se considera que se utilizaron todos los estudios apropiados y disponibles, entonces, la heterogeneidad es grande (I2 = 99.8 %). La heterogeneidad se mantiene, incluso si se elimina el estudio en Italia del conjunto de los ocho modelos (en este caso, la I2 calculada es igual a 99.1 %). En general, el tamaño de la muestra no parece estar altamente correlacionado con el tamaño del efecto (el volumen).
La densidad de la masa afecta la forma de los árboles. La baja densidad de las masas conduce a mayor ahusamiento del árbol (Philip, 1994; Smith, Larson, Kelty, & Ashton, 1997). Por otra parte, la posición de un árbol en la masa influye en su forma, pues los árboles suprimidos muestran menor ahusamiento, mientras que en los árboles dominantes es mayor (Smith et al., 1997). Lo mencionado anteriormente es el resultado de la distribución de los anillos de árboles a lo largo del tronco (ver Smith et al., 1997; Wilson, 1984). Las condiciones de competencia afectan la distribución del crecimiento del diámetro a diferentes alturas hasta el tronco, que influyen en la forma y ahusamiento del árbol, mientras que el ahusamiento cambia a medida que las condiciones de crecimiento se modifican durante su vida (Smith et al., 1997; Wilson, 1984).
Un árbol con mayor ahusamiento tiene menor volumen comparado con uno de menor ahusamiento, teniendo el mismo diámetro a la altura del pecho. Como resultado, las diferencias de volumen entre los bosques europeos pueden deberse a diferentes condiciones de competencia, en relación con las densidades de las masas y posiciones de los árboles, y no a las distintas condiciones geográficas (clima). Esa puede ser la razón para que el estudio realizado en Grecia se pueda usar entre los volúmenes de los estudios escandinavos, como se muestra en la Figura 1. Las distintas condiciones de competencia reflejan el resultado de las diferentes dinámicas de masa y regímenes de adelgazamiento (Oliver & Larson, 1996; Smith et al., 1997).
Conclusiones
A partir del metanálisis para el volumen de P. sylvestris en Europa, se obtuvieron las siguientes conclusiones: una mayor investigación podría ser útil en Italia (los volúmenes parecen ser muy pequeños). En Grecia, existen volúmenes grandes de la especie en comparación con aquellos en Suecia; sin embargo, un estudio de Grecia con un tamaño de muestra mayor podría contribuir para fomentar la investigación. Existe gran heterogeneidad entre las masas en toda Europa en relación con el volumen de la especie, lo que indica condiciones de competencia distintas como resultado de las diferentes dinámicas de las masas y regímenes de adelgazamiento, que afectan el ahusamiento de los árboles durante su vida. Para futuras investigaciones, se propone la aplicación de un metanálisis con el uso del tamaño del efecto para el metanálisis de varianza (meta-ANOVA) y metarregresión.
References
Bazire, P., & Gadant, J. (1991). La forêt en France. Paris: La Documentation Française. [ Links ]
Borenstein, M., Hedges, L., & Higgins, J. (2009). Introduction to meta-analysis. Chichester, UK: John Wiley & Sons. [ Links ]
Boratynski, A. (1991). Range of natural distribution. In M. Giertych, & C. Matyas (Eds.), Genetics of Scots pine (pp. 19-30). Amsterdam: Elsevier. [ Links ]
Christie, M., & Lines, R. (1979). A comparison of forest productivity in Britain and Europe in relation to climatic factors. Forest Ecology Management, 2, 75‒102. doi: 10.1016/0378-1127(79)90039-2 [ Links ]
Cooper, H. (2010). Research synthesis and meta-analysis. Los Angeles, CA, USA: Sage Publications. [ Links ]
Corona, P., & Ferrara, A. (1987). Dendrometrical investigations on Pinus silvestris in Trentino-Alto Adige. Monti e Boschi, 38(6), 51-54. [ Links ]
DerSimonian, R., & Laird, N. (1986). Meta-analysis in clinical trials. Controlled Clinical Trials, 7(3), 177−188. doi: 10.1016/0197-2456(86)90046-2 [ Links ]
Egger, M., Smith, G., Schneider, M., & Minder, C. (1997). Bias in meta-analysis detected by a simple, graphical test. British Medical Journal, 315(7109), 629−634. doi: 10.1136/bmj.315.7109.629 [ Links ]
Hardy, R., & Thompson, S. (1998). Detecting and describing heterogeneity in meta-analysis. Statistics in Medicine, 17(8), 841−856. doi: 10.1002/(SICI)1097-0258(19980430)17:8<841::AID-SIM781>3.0.CO;2-D [ Links ]
Higgins, J., Thompson, S., Deeks, J., & Altman, D. (2003). Measuring inconsistency in meta-analyses. British Medical Journal, 327(7414), 557−560. doi: 10.1136/bmj.327.7414.557 [ Links ]
Kitikidou, K., Milios, E., & Lipiridis, I. (2014). Tree volume estimates and nearest neighbor analysis in the stands of scots pine (Pinus sylvestris) in the central part of Rodope mountain. Šumarski list, 138(11-12), 573‒582. Retrieved from http://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=199404 [ Links ]
Kitikidou, K., Milios, E., Stampoulidis, A., & Papageorgiou, A. (2013). Application of meta-analysis in forestry related topics. Forest Systems, 22(3), 578−581. doi: 10.5424/fs/2013223-04766 [ Links ]
Laasasenaho, J. (1982). Taper curve and volume functions for pine, spruce and birch. Helsinki, Finland: Finnish Forest Research Institute [ Links ]
Laasasenaho, J., & Sevola, Y. (1971). Mänty- ja kuusirunkojen puutavarasuhteet ja kantoarvot. Helsinki, Finland: Finnish Forest Research Institute. [ Links ]
Lau, J., Ioannidis, J., Terrin, N., Schmid, C., & Olkin, I. (2006). The case of the misleading funnel plot. British Medical Journal, 333(7568), 597−600. doi: 10.1136/bmj.333.7568.597 [ Links ]
Lipsey, M., & Wilson, D. (2001). Practical meta-analysis. Thousand oaks. California: Sage Publications. [ Links ]
Mantel, N., Haenszel, M. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22(7), 19−48. doi: 10.1093/jnci/22.4.719 [ Links ]
Mencuccini, M., & Bonosi, L. (2001). Leaf/sapwood area ratios in Scots pine show acclimation across Europe. Canadian Journal of Forest Research, 31, 442−456. doi: 10.1139/x00-173 [ Links ]
Ministry of Agriculture. (1992). Results of the first national forest inventory. Athens: Publication of Department of Forest Mapping. [ Links ]
Näslund, M. (1947). Funktioner och tabeller för kubering av stående träd. Stockholm, Sweden: Meddelanden från Statens skogsforskningsinstitutet. Retrieved from http://pub.epsilon.slu.se/9900/1/medd_statens_skogsforskningsinst_036_03.pdf [ Links ]
Oliver, C., & Larson, B. (1996). Forest stand dynamics. New York, USA: Wiley. [ Links ]
Panagiotakos, D. (2006). Research methodology and data analysis for the health sciences. Athens, Greece: Kostaki Publications. [ Links ]
Papakosta, M., Kitikidou, K., Bakaloudis, D., & Vlachos, C. (2014). Dietary variation of the stone marten (Martes foina): A meta-analysis approach. Wildlife Biology in Practice, 10(2), 85-101. doi: 10.2461/wbp.2014.10.11 [ Links ]
Philip, M. (1994). Measuring trees and forests. UK: CAB International. [ Links ]
Poyatos, R., Martínez-Vilalta, J., Čermák, J., Ceulemans, R., Granier, A., Irvine, J., Mencuccini, M. (2007). Plasticity in hydraulic architecture of Scots pine across Eurasia. Oecologia, 153, 245−259. doi: 10.1007/s00442-007-0740-0 [ Links ]
Sevola, Y. (1998). Statistical yearbook of forestry. Helsinki, Finland: Finnish Forest Research Institute . [ Links ]
Smith, D., Larson, B., Kelty, M., & Ashton, M. (1997). The practice of silviculture: Applied forest ecology. New York, USA: Wiley. [ Links ]
Sterne, J., & Egger, M. (2001). Funnel plots for detecting bias in meta-analysis. Journal of Clinical Epidemiology, 54(10), 1046−1055. doi: 10.1016/s0895-4356(01)00377-8 [ Links ]
Van Laar, A., & Akça, A. (1997). Forest mensuration. Göttingen, Germany: Cuvillier Verlag. [ Links ]
Wilson, B. (1984). The growing tree. USA: University of Massachusetts Press. [ Links ]
Recibido: 16 de Noviembre de 2015; Aprobado: 15 de Septiembre de 2016











 texto en
texto en 


