Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias forestales
versión impresa ISSN 2007-1132
Rev. mex. de cienc. forestales vol.12 no.68 México nov./dic. 2021 Epub 28-Feb-2022
https://doi.org/10.29298/rmcf.v12i68.814
Scientific article
Models to determine the commercial volume of Bursera simaruba (L.) Sarg. and of Metopium brownei (Jacq.) Urb. in Quintana Roo, México
1Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Campo Experimental Chetumal. México.
2Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Campo Experimental San Martinito. México.
3Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Campo Experimental Saltillo. México.
4Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Campo Experimental Valle de México. México.
The state of Quintana Roo occupies the second national place in timber production of broadleaf species, of which Bursera simaruba and Metopium brownei are relevant, from the value of their wood and wide distribution. The functions that estimate the stem and commercial volume, in addition to the taper and the volume ratio are important in the elaboration of a forest management program. The aim of this study was to fit a nonlinear function that estimates trade volume for two species in central and southern Quintana Roo. A commercial volume model with random effects was fitted at the tree level, using the mensuration data from 188 and 133 trees for each species, respectively, and all the diameter categories found in these forest ecosystems were covered. The best combinations of inclusion of the random effects were chosen according to the maximum likelihood. The proposed equations have an average bias when estimating the commercial volume for the two species of 0.0045 m3 and an explanation greater than 90 % of the sample variability. The resulting equations may be used in the timber estimation of the sustainable forest management programs of tropical forests at the central and southern territories of the state.
Key words Tropical forest; product distribution; forest management; cubing system; Quintana Roo; volume
El estado de Quintana Roo ocupa el segundo lugar nacional en producción maderable de especies latifoliadas; de ellas, Bursera simaruba y Metopium brownei son de relevancia forestal debido al valor de su madera y amplia distribución en la entidad. Para elaborar programas de manejo forestal, las funciones que estiman el volumen fustal y comercial, además del ahusamiento y la razón de volumen son importantes. El objetivo del presente estudio fue ajustar una función no-lineal que estime el volumen comercial para dos taxa en el centro y sur de Quintana Roo, México. Con información dasométrica de 188 y 133 árboles, respectivamente que abarcaron todas las categorías diamétricas observadas en estos ecosistemas forestales; se ajustó un modelo de volumen comercial con efectos aleatorios a nivel de árbol, y se eligieron las mejores combinaciones de inclusión de los efectos aleatorios según la máxima verosimilitud. Las ecuaciones propuestas tienen un sesgo, en promedio, al estimar el volumen comercial para los dos taxones de 0.0045 m3 y una explicación mayor a 90 % de la variabilidad muestral. Las ecuaciones resultantes podrán emplearse en la estimación maderable en los programas de manejo forestal sustentable de los bosques tropicales ubicados en el centro y sur del estado.
Palabras clave Bosque tropical; distribución de productos; manejo forestal; sistema de cubicación; Quintana Roo; volumen
Introduction
The state of Quintana Roo (Q. Roo) occupies the second national place in timber production of broad-leaved species, with an approximate harvest of 47 139 m3 of roundwood (m3 mr) of common tropical species (12.10 % of national production) and of 4 807 m3 mr of precious species (15.18 % of national production), with a value of about $ 84 091 064 and $ 17 306 518, respectively, which places it with a contribution to GDP below 0.2 % registered at national level, according to the Ministry of Environment and Natural Resources (Semarnat, 2017). Bursera simaruba (L.) Sarg. (Chakáh) and Metopium brownei (Jacq.) Urb. (Chechem negro) are common tropical species of commercial interest for the forestry industry (Silva et al., 2011; Gallegos et al., 2012), they are widely distributed in the Peninsula of Yucatán (Herbario CICY, 2010), are used for agroforestry for their growth and regeneration (Bursera simaruba) as well as for the production of furniture and handicrafts (Metopium brownei) (Román et al., 2016; ITTO, 2020).
The accurate estimation of the stem volume, of the total volume when including the branches, and of the commercial volume based on the dimensions that the market demands, is important to develop the silvicultural practices proposed in the forest management plan according to the data of the forest inventories carried out (Corral-Rivas and Návar-Cháidez, 2009; Diéguez-Aranda et al., 2009; Gómez-García et al., 2016; Tamarit et al., 2017; Niño et al., 2018).
Mathematical modeling is a support tool for forest resource managers, for which the adjustment of models that estimate the stem, total and commercial volume; o model, with precision, the ratio between the commercial volume and the stem (Vc / Vf), as well as its dynamics of decrease in the accumulated volume of a tree with the increase in height and the reduction of the diameter on the stem until reaching to the total height (volume ratio functions), in addition to describing the taper of the trees (diameter at different heights) by species, contributes to making management plans according to the specific and current conditions of the resources (Burkhart, 1977; Tapia and Návar, 2011; Barrios et al., 2014; Özçelik and Göçeri, 2015; Hernández-Ramos et al., 2018a).
In recent years in Mexico, modeling has been carried out through functions that consider diameters at different heights on the stem and compatible commercial taper-volume systems for different species of the Pinus genus (Tapia and Návar, 2011; Quiñonez-Barraza et al., 2014; Tamarit et al., 2016; Silva et al., 2018), or by volume ratio models for species such as Eucalyptus urophylla Blake in Huimanguillo, Tabasco, Swietenia macrophylla King in Quintana Roo and Pinus pseudostrobus Lindl. in San Juan Nuevo Michoacán, among others (Hernández-Ramos et al., 2018a; García-Espinoza et al. 2018).
Commercial volume systems composed of ratio models are a tool to accurately calculate the commercial volume and the distribution of timber products from standing trees (Prodan et al., 1997; Hernández-Ramos et al., 2018a; García-Espinoza et al., 2018). The estimation of these volumes is fundamental in the projection of the use of the timber resource and the yield for the forest industry, because they make it possible to estimate the financial income of the forest from forest inventory data, mainly the distribution of products per unit area. (Niño et al., 2018; Silva et al., 2018); and they also contribute to avoiding the overuse of species of commercial importance in general, not only of tropical forests.
For the area of interest, Hernández-Ramos et al. (2018a and 2018b) adjusted total volume models and generated a commercial volume system from ratio models, in addition to a segmented taper system (d) compatible with commercial volume (Vc) for Swietenia macrophylla King (mahogany) in tropical forests of Quintana Roo. López et al. (2019) adjusted a compatible system of commercial volume equations consisting of stem, branches and stem and thick branches of trees for 11 important tropical species in southeastern Mexico.
Traditionally, the equations to design these commercial volume systems have been adjusted using linear and non-linear regression models that assume normality, equality of variances and independence of errors (Carrero et al., 2008).
However, obtaining reliable equations for some variables is complex, due to the variability that exists in these relationships due to the effect of the different forms of the stems and the conditions in which each individual develops (Quiñonez et al., 2012). At present, the adjustment under the approach of mixed effects models (MEM) has become a viable option for this type of study (Corral-Rivas et al. 2014), since with its incorporation in its parameters it allows grouping the sources of variability and reduce the variance of the error (Seoane, 2014). This MEM technique includes in its formulation fixed parameters common to the entire population and specific random parameters for each level of grouping (Seoane, 2014). As a result, more efficient, precise and reliable estimators result than the fixed parameters of the model and, therefore, estimates can be made with greater certainty of the variable of interest (Carrero et al., 2008). For all the above, the objective of the present study was to fit a non-linear function with random effects that estimates the commercial volume for Bursera simaruba and Metopium brownei in central and southern Quintana Roo, Mexico.
Materials and Methods
The study was carried out in different forest areas of Quintana Roo, Mexico, which are located in areas with topoforms of low hills and rocky plains at an altitude of 20-180 m. The predominant climate is warm subhumid (Aw), with an average annual temperature of 22 °C and an average rainfall of 1 300 mm (Semarnat, 2014).
From tours in the forest areas of the state, trees larger than 7.5 cm in normal diameter were selected randomly located in undisturbed areas of the tropical forest, where 188 specimens of Bursera simaruba and 133 of Metopium brownei were sampled, with which they were covered all the diameter categories found in these forest ecosystems (10-50 and 10-60 cm, respectively). Information on stump diameter (dt), normal diameter (d), total height (H), and partial diameters and heights on the stem (d i and h i ) were taken from each of them. The sample was chosen with monopod trees, without the presence of mechanical damage or pests or diseases, in addition to being at least 20 m away from roads, clearings or places with clearings to avoid edge effects. The descriptive statistics of the analyzed variables are arranged in Table 1.
Table 1 Descriptive statistics of the sample of Bursera simaruba (L.) Sarg. and Metopium brownei trees (Jacq.) Urb.
| Statistics | Species | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bursera simaruba | Metopium brownei | |||||||||
| d | H | Vt | R | Vc | d | H | Vt | R | Vc | |
| Average | 23.82 | 13.97 | 0.4938 | 0.44 | 0.2143 | 30.00 | 15.45 | 0.6820 | 0.46 | 0.3174 |
| Typical error | 0.24 | 0.08 | 0.0110 | 0.01 | 0.0080 | 0.30 | 0.09 | 0.0140 | 0.01 | 0.0120 |
| Standard deviation | 9.21 | 3.19 | 0.4360 | 0.38 | 0.3200 | 10.13 | 3.11 | 0.4840 | 0.37 | 0.3950 |
| Coefficient of variation | 38.66 | 22.88 | 88.2900 | 87.05 | 149.2900 | 33.77 | 20.13 | 70.9600 | 81.52 | 124.4300 |
| Variance | 84.79 | 10.22 | 0.1900 | 0.14 | 0.1020 | 102.64 | 9.67 | 0.2350 | 0.14 | 0.1560 |
| Curtosis | -0.50 | -0.60 | 1.5000 | -1.50 | 2.3000 | -0.60 | 0.50 | -0.1000 | -1.60 | 3.2000 |
| Coefficient of asymmetry | 0.60 | -0.10 | 1.4000 | 0.50 | 2.6000 | 0.20 | -0.50 | 0.8000 | 0.40 | 1.9000 |
| Minimum | 7.00 | 5.57 | 0.0239 | 0.01 | 0.0013 | 9.40 | 4.63 | 0.0337 | 0.02 | 0.0028 |
| Maximum | 49.80 | 21.80 | 2.1000 | 1.00 | 2.1000 | 57.30 | 23.10 | 2.3000 | 1.00 | 2.3000 |
d = Normal diameter (cm); H = Total height (m); Vt = Total volume (m3);
R = Volume ratio (m3); Vc = Commercial volume (m3).
The measurements of the diameters (di) at different heights on the stem (h i ) of 0.3 m, 0.6 m, 0.9 m, 1.3 m and 2.5 m, were made directly with a caliper graduated to the millimeter, while the rest of h i and d i with a Bitterlich Telerelascope along the shaft where possible from 2.5 m to full height (H) or zero diameter (d 0 ). For the calculation of the stem volume (Vf) the volumes of the different sections (logs) were added, which were determined by the Smalian formula and for the volume of the tip or last log (Vp) with the cone formula; the volume ratio (R) resulted from the ratio between the volume at different sections on the stem (Vi) and the Vf, for which the expression Vi/ Vf was used (Balzarini et al., 2005; Hernández-Ramos et al. , 2018a; García-Espinoza et al. 2018).
As indicated in the Official Mexican Standard NOM-152-SEMARNAT-2006, a non-linear function (general model) for each species was adjusted, which is made up of two components: the first one includes a mathematical structure that corresponds to an equation of Vf (a 0 +a 1 (d 2 H/1000) and the second one is an equation referring to the ratio between the volumes of the sections and the R (e (-(a2)*((di/d)/1000) e (a3*(di/d)) ), while these equations, when multiplied, estimate the commercial volume (Vc) (Schabenberger and Pierce, 2002; Balzarini et al., 2005) (Table 2).The latter is defined by the dimensions that the sawmill industry or timber products demand, in which there is an interest in estimating, whether long dimensions or primary, short or secondary and waste or firewood. For the two species, the general model and the random effect additive to each combination of the fixed parameters were tested and eight expressions were obtained from the general model.
Table 2 Adjusted commercial volume models with fixed and random effects for Bursera simaruba (L.) Sarg. and Metopium brownie (Jacq.) Urb.
| Identifier | Structure of the models |
|---|---|
| General Identifier |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
d = Normal diameter (cm); d i = Diameter at different heights on the stem;
H = Total height (m); Vc = Commercial volume; a 0 , a 1, a 2 and a 3 = Parameters to be estimated; +u = Random effect; e = Exponential function.
The general model (Table 2) was first adjusted by ordinary least squares (OLS) and two variants of Spurr's (1952) shaft volume equation: a linear one of the y =a 0 +a 1 X form, and the second one of the exponential type y = aX b form. In them, y is the response variable (Vf = stem volume), X represents the independent variable included in the model (d 2 H), a and b correspond to the parameters to be estimated.
The incorporation of the random effect to the fixed parameters (a i + u) was done per tree to explain the variability in its tapers, considering the biological meaning of each one; for example, by including the random effect in the parameter referring to the shape of the tree, the rate of change of the geometric body in the stem, the ratio of proportion between the stem volume and the commercial volume or in all three simultaneously within each of the components in the proposed non-linear function, where the probability value of the effect must be significant (P ≥ 0.05) (Table 1, 1-16).
The adjustment was carried out in the SAS 9.3® program using the nlmixed procedure and the FIRO first order method, which defines with greater precision the approximation by likelihood of the values in the estimated parameters (Beal and Sheiner, 1982; SAS, 2011) The distribution for both the dependent variables and the random effects (a i + u) was specified in the programming as NORMAL to be adjusted by the Dual Quasi-Newton optimization technique and the Adaptive Gaussian Square integration method of the Statistical Analysis System (SAS, 2011).
The selection of the best combination when including the random effects within the non-linear model, was made through the significance of the estimated parameters in both fixed and random effects at a value of 95 % reliability (P ≥ 0.05), and the best values of Verisimilitude-2Log and Information Criterion of Corrected Akaike (CIAC, for its acronym in Spanish) (García and Rapelli, 2011; Gómez-García et al., 2016). Furthermore, for the best expression, the trend in the estimates was graphically verified by using the model structures separately in the stem volume (Vf = first mathematical structure) and volume ratio (R = second mathematical structure), and so joint to estimate the commercial volume (Vc) of each species or up to a diameter of 20 cm (Table 1, general model).
In the selected model, the homoscedasticity of the residuals was verified using White's test, under the hypothesis that the residuals are homogeneously distributed around zero (null hypothesis: Ho), while the alternative hypothesis refers to a homoscedastic distribution of the residuals (alternative hypothesis: Ha) at a 95 % reliability level (Martínez et al., 2006). The quality of the estimates for the variables Vf, R and Vc was determined through bias (E) (Quevedo et al., 2010) and the coefficient of determination (R 2 ) and through the graphic analysis of the observed values against the values estimates of each variable (Pece, 1994).
Results
When adjusting the general model and the variations in the inclusion of random effects, it was observed that both the general structure of the model and expressions 1, 2, 4 and 5 for Bursera simaruba and 1, 2, 4 and 5 for Metopium brownei, in some of its fixed parameters, they were not significant at 95 % reliability (P ≥ 0.05). While, in the combinations of inclusion of the random effects of expressions 6 and 8 in both species, the parameters related to mixed affects could not be estimated even when they tried to adjust by the Gauss-Hermite method (Pinheiro and Bates, 1995). Therefore, these models were discarded for further analysis and were not included in Table 3. Due to this situation, only the combinations of inclusion of the random parameters of expressions 3 and 7 for Bursera simaruba and Metopium brownei trees are presented for subsequent analyzes, in which all were significant (P ≥ 0.05) when adjusted with 1 476 and 1 130 pairs of data, respectively.
Table 3 Estimated parameters for the different expressions of the adjusted commercial volume model for Bursera simaruba (L.) Sarg. and Metopium brownie (Jacq.) Urb.
| Species | System | Parameter | Estimator | Eea | t Value | Pr>|t| | ICI | ICS |
|---|---|---|---|---|---|---|---|---|
| Bursera simaruba | 3 | a0 | 0.01238 | 0.0059 | 2.09 | 0.0381 | 0.00068 | 0.02407 |
| a 1 | 0.04866 | 0.0011 | 42.69 | <0.0001 | 0.04642 | 0.05091 | ||
| a 2 | 9.15250 | 0.9572 | 9.56 | <0.0001 | 7.26420 | 11.04070 | ||
| a 3 | 5.32220 | 0.1084 | 49.09 | <0.0001 | 5.10840 | 5.53610 | ||
| se | -0.04927 | 0.0009 | -50.28 | <0.0001 | -0.05121 | -0.04734 | ||
| su1 | 0.00861 | 0.0006 | 13.71 | <0.0001 | 0.00737 | 0.00985 | ||
| su2 | 0.91109 | 0.1575 | 5.79 | <0.0001 | 0.60120 | 1.22250 | ||
| 7 | a 0 | 0.05710 | 0.0024 | 23.37 | <0.0001 | 0.05228 | 0.06192 | |
| a 1 | 0.94400 | 0.0200 | 47.09 | <0.000 1 | 0.90440 | 0.98350 | ||
| a 2 | 9.18550 | 0.9675 | 9.49 | <0.0001 | 7.27700 | 11.09400 | ||
| a 3 | 5.32100 | 0.1092 | 48.73 | <0.0001 | 5.10560 | 5.53640 | ||
| se | -0.04964 | 0.0009 | -50.26 | <0.0001 | -0.05158 | -0.04769 | ||
| su1 | -0.07213 | 0.0062 | -11.45 | <0.0001 | -0.08456 | -0.05971 | ||
| su2 | -0.93620 | 0.1633 | -5.73 | <0.0001 | -1.25830 | -0.61400 | ||
| Metopium brownei | 3 | a 0 | 0.00807 | 0.0118 | 0.68 | 0.4977 | -0.01541 | 0.03155 |
| a 1 | 0.04111 | 0.0013 | 29.79 | <0.0001 | 0.03838 | 0.04384 | ||
| a 2 | 3.08900 | 0.5345 | 5.78 | <0.0001 | 2.03160 | 4.14640 | ||
| a 3 | 6.30480 | 0.1792 | 35.18 | <0.0001 | 5.95030 | 6.65930 | ||
| se | -0.07122 | 0.0016 | -43.68 | <0.0001 | -0.07444 | -0.06799 | ||
| su1 | -0.00954 | 0.0007 | -12.65 | <0.0001 | -0.01103 | -0.00805 | ||
| su2 | 0.36620 | 0.0785 | 4.66 | <0.0001 | 0.21090 | 0.52150 | ||
| 7 | a 0 | 0.04722 | 0.0040 | 11.57 | <0.0001 | 0.03914 | 0.05529 | |
| a 1 | 0.95240 | 0.0333 | 28.58 | <0.0001 | 0.88650 | 1.01830 | ||
| a 2 | 3.09670 | 0.5375 | 5.76 | <0.0001 | 2.03330 | 4.16000 | ||
| a 3 | 6.30360 | 0.1798 | 35.06 | <0.0001 | 5.94800 | 6.65930 | ||
| se | -0.07144 | 0.0016 | -43.52 | <0.0001 | -0.07468 | -0.06819 | ||
| su1 | -0.08848 | 0.0079 | -11.1 | <0.0001 | -0.10430 | -0.07271 | ||
| su2 | 0.37550 | 0.0810 | 4.63 | <0.0001 | 0.21520 | 0.53580 |
a 0 , a 1, a 2 and a 3 = Fixed effect parameters; su 1 and su 2 = Standard deviation of random effects; Eea = Estimator standard error; se= Standard deviation of the residuals in the system; ICI and ICS = Confidence intervals of the lower and upper estimates, respectively.
For the two species, the combination in the mathematical structure that contains the Spurr stem volume model in its exponential form, presents the highest statistical values in the likelihood indicators -2Log and CIAC, for which the structures of model 7 were selected for Bursera simaruba and Metopium brownei, respectively. When contrasting these values with those obtained when adjusting the general model by ordinary least squares (OLS), an average statistical gain is observed when applying the mixed effects models approach of 5.6 % and 6.9 % for Bursera simaruba and Metopium brownei, respectively (Table 4). In addition, White's tests for both species were not significant (a < 0.05), which indicates that the residuals of both models are distributed in a homoscedastic way, which is why the null hypothesis (Ho) is accepted and Ha is rejected.
Table 4 Statistical fit indicators of the adjusted trade volume model for Bursera simaruba (L.) Sarg. and Metopium brownie (Jacq.) Urb.
| Species | Bursera simaruba | Metopium brownei | ||||
|---|---|---|---|---|---|---|
| Random
effects model |
General
model |
3 | 7 | General
model |
11 | 15 |
| Verisimilitude -2 Log | -4 617 | -4 368 | -4 360 | -2 588 | -2 409 | -2 396 |
| CIAC | -4 601 | -4 354 | -4 346 | -2 543 | -2 395 | -2 382 |
CIAC = Information Criterion of Corrected Akaike.
The biases estimated for the two species show good precision in the estimates when evaluating them individually for Vf and R, and as a complete model to estimate Vc, since in all cases they are less than 0.03 m3 (Table 5). In addition, when performing the graphical evaluation and by means of a regression of the observed values against those predicted by the variable of interest, no obvious problems were observed in the estimates, a situation that is reflected in the value of the determination coefficient (R 2) that in all cases was greater than 0.9 (Figure 1).
Table 5 Estimated bias by independent variable in the adjusted commercial volume model.
| Independiente variable | Vf (m3) | R (Vi/Vf) | Vc (m3) |
|---|---|---|---|
| Model including the random effects | Sesgo (E) | ||
| 7. Bursera simaruba (L.) Sarg. | -0.012543 | 0.029831 | -0.001384 |
| (R2= 0.95) | (R2= 0.93) | (R2= 0.94) | |
| 7. Metopium brownei (Jacq.) Urb. | 0.014684 | 0.019924 | 0.008979 |
| (R 2 = 0.93) | (R 2 = 0.94) | (R 2 = 0.92) | |
Vf = Stem volume; R = Volume ratio based on diameter; Vi = Volume at different sections on the shaft; Vc = Commercial volume; R 2 = coefficient of determination of the observed values against the predicted values.
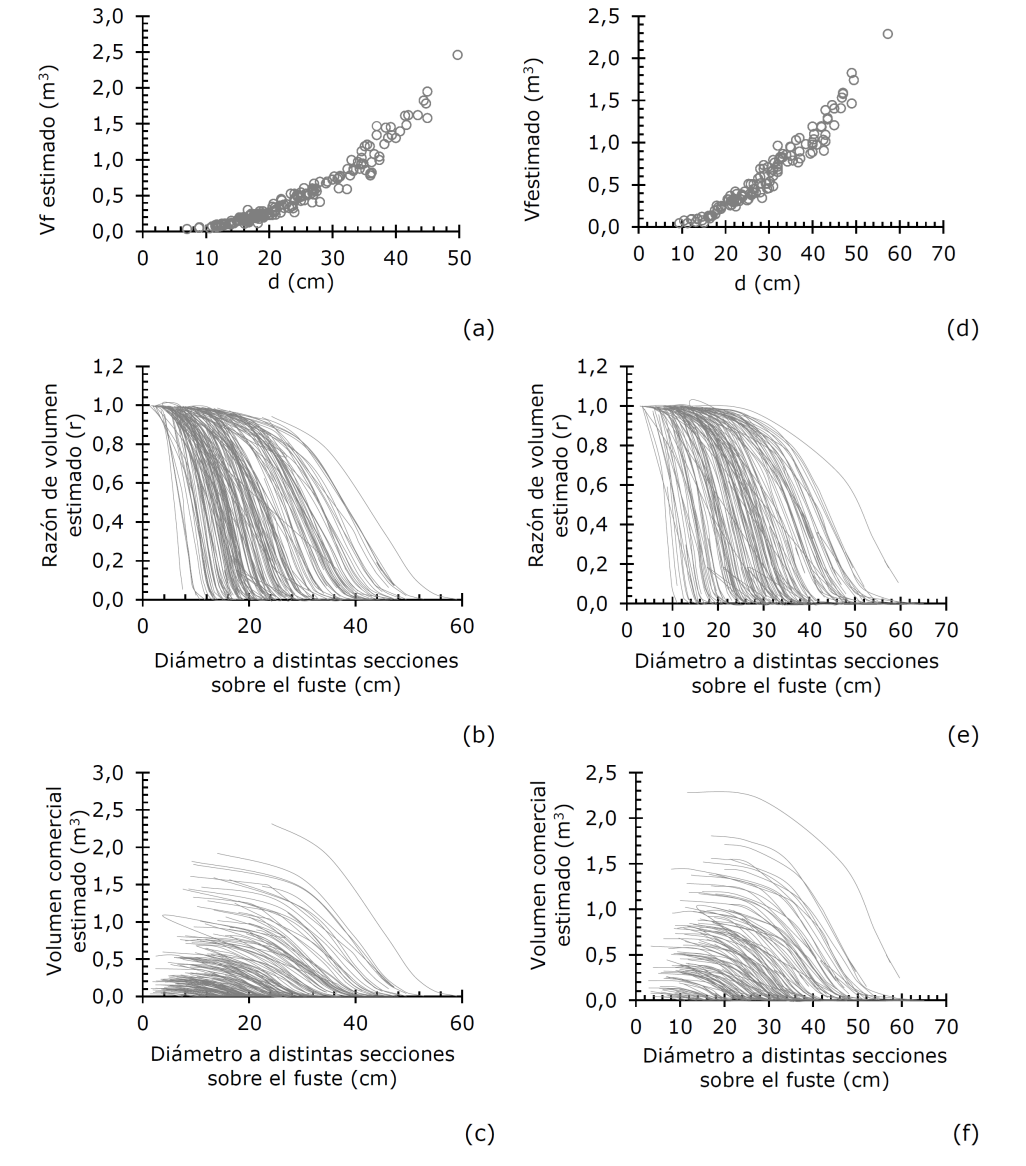
Figure 1 Trend of stem volume estimates, volume ratio and commercial volume for Bursera simaruba (L.) Sarg. (1a, 1b and 1c) and Metopium brownei (Jacq.) Urb. (1d, 1e and 1f) species.
To exemplify the use of the structure that best fit the observed data of the commercial volume model, the values of normal diameter (d) = 30 cm and total height (H) = 15 m for Bursera simaruba, and d = 40 cm and H = 20 m for Metopium brownei, using model 7 with its parameters for each species, respectively, to estimate the stem volume (Vf) and volume ratio (R) when using the two sections of the model separately and when applying the complete model adjusted for commercial volume (Vc). From the general expression of the model, the first component corresponding to Vf is taken, which, when substituting for Bursera simaruba there is:
Vf = 0.0571 ((30 2 · 15)/1000)0.9440 = 0.6663 m3
And for Metopium brownei: Vf = 0.0472 ((40 2 · 20)/1000)0.9524 = 1.5049 m3.
Next, the minimum diameter for primary products is established, which in this case was 20 cm; then the second section of the general model is taken and the values are substituted, for which the following results for Bursera simaruba:
R =Exp(-9.1855·((20/30)/1000)·Exp(5.321*(20/30)))= 0.8085, y para Metopium brownei: R = Exp(-3.0967·((20/40)/1000)·Exp(6.3067*(20/30))) = 0.9644.
Finally, to obtain the Vc at the established minimum cutting diameter, the values of Vf and R are multiplied, or the proposed model of each species is applied directly,: for Bursera simaruba as follows:
Vc = [0.0571 ((30 2 · 15)/1000)0.9440]([Exp(-9.1855·((20/30)/1000)·Exp(5.321*(20/30)))] = 0.5387 m3, y para M. brownei:
Vc = [0.0472((40 2 · 20)/1000)0.9524] [Exp(-3.0967·((20/40)/1000)·Exp(6.3067*(20/30)))] = 1.4514 m3 .
Discussion
The MEM allows correcting the structure of variances-covariances associated with the classification variables of the trees (Littell et al., 2006), since by grouping the information in class, under the MEM approach, the error is reduced, since the variability between the classes is explained by the inclusion of random parameters, which are estimated simultaneously with the fixed parameters (Castedo et al., 2006; Corral et al. 2019). In this analysis technique (MEM), it assumes that the variance is specific for each classification level (Seoane, 2014), so it is possible to increase the R 2 and improve other goodness-of-fit criteria, such as the AIC and BIC.
In the evaluated models, random effects were included to account for the effect of classification covariates during adjustment in the equations. In this case, the random effect was specific at each level of the classification factor, which according to De los Santos et al. (2006), Tamarit-Urias et al. (2014) and García-Espinoza et al. (2019) allows obtaining more efficient, precise and reliable estimators of the fixed parameters of the model and predicting specific random parameters of each sample unit, which reflect the deviation pattern with respect to the mean, but after adjustment, the values obtained from the fit for the random parameters are not used to construct the predictions, so the parsimony of the models is not modified.
In the case of the structure of the volume model 3 for Bursera simaruba, and 7 for M. brownei, all the parameters were significant (P ≥ 0.05) (Table 3), similar to that reported by Quevedo et al. (2010), these authors analyzed the stem volume models under the mixed effects approach for Tabebuia rosea (Bertol.) In Venezuela, where a grouping by diameter category and transformation of the dependent variable was performed. In a similar way to the study carried out by Gómez-García et al. (2016), who developed a profile function through mixed effects for Pinus sylvestris L. in Turkey, and where it was adjusted by the FIRO (first-order) method, of the R-project program, which is the same method used in this work.
For the choice of model 3 and 7 of Table 1 for Bursera simaruba and Metopium brownei, respectively, the description by García and Rapelli (2011) was taken as a reference, who reported that the models with the values closest to zero in the indicators of Verisimilitude -2Log and CIAC have a higher likelihood in the fit. In addition, these values were consistent with the evaluation criteria made by Gómez-García et al. (2016); and by Quiñonez-Barraza et al. (2014), who adjusted compatible commercial taper-volume systems for the main Pinus species from Durango, Mexico.
The bias values in the models proposed by species and the determination coefficients (R 2) obtained by contrasting the observed data against those predicted by the variable of interest (Vf, R and Vc), coincide with that reported by Pece (1994), who used a volume ratio model to estimate the commercial volume in Eucalyptus pellita F. Muell. in Brazil and obtain biases when calculated by diameter category between 0.06 and 0.11. Furthermore, it is similar to that determined by Hernández-Ramos et al. (2017), by proposing volume ratio systems for Eucalyptus urophylla in Tabasco and obtaining accurate estimates with lower biases in the variables of Vt, R and Vc than those obtained in this work (< 0.0077) and R2 when contrasting the estimated values versus observed greater than 0.94.
Likewise, the precision of the estimates obtained by this work in commercial volume (Vc) are similar to that recorded by Hernández-Ramos et al. (2018b) when using volume ratio systems in Swietenia macrophylla trees in Quintana Roo and obtaining biases for volume ratio structures based on normal diameter and total height of -0.0121 and 0.0053, respectively. However, they differ with García-Espinoza et al. (2018) by proposing structures based on the volume ratio for P. pseudostrobus in Michoacán, and registering good accuracy in the estimates and a lower bias in the Vc compared to those obtained in this work (< 0.001 m3).
The graphical evaluation of the trends in the estimates (Figure 1) agrees with that obtained by Tapia and Návar (2011) who adjusted models of stem volume and taper for P. pseudostrobus in Nuevo León;Tamarit-Urias et al. (2016), by modeling the stem profile of nine species of the Pinus genus, and obtaining projections according to the trends of the observed data. It also coincides with those reported by Tamarit et al. (2017) in the construction of a cubing system for individual trees for the Quercus genus in Puebla and those reported by Silva et al. (2018), who constructed compatible taper and commercial volume functions for three Pinus species in Chihuahua.
These tools generated at work can be complemented with the equations proposed by García et al. (2017), which propose to estimate the stem volume through the dimensions of the stump diameter in Bursera simaruba and Metopium brownei in the tropical forests of Quintana Roo, and can be taken as an update of the equations proposed by De los Santos (1976) and Patiño et al. (1994) for these two species.
Conclusions
The proposed volume models based on diameter at different heights above the stem are reliable to estimate the stem volume when using the first part of the equation, the volume ratio when using the second part, and the commercial volume when used together in these two species. This is a very significant advantage if it is compared with equations generated more than 30 years ago to estimate clean stem volume or total stem volume for large trees, which does not correspond to the diameters that are used today. With the mathematical structures proposed by species, it will be possible to build product distribution tables to project the timber yields of areas under forest use, according to the current conditions of the Bursera simaruba (Chakáh) and Metopium brownei (Black Chechem) species in tropical forests of the central and southern state of Quintana Roo, Mexico.
It is necessary to carry out this type of study in Quintana Roo, in order to cover at least the 30 main species that are most important from a commercial point of view.
Acknowledgements
This research was sponsored by the government of the state of Quintana Roo through the Forest Institute (INFOQROO) through the project "Study to carry out actions of tables of volumes of 8 timber forest species". SINCOP-INIFAP 232179Y.
REFERENCES
Balzarini, M., R. Macchiavelli y F. Casanoves. 2005. Aplicaciones de modelos mixtos en agricultura y forestería. Turrialba, Costa Rica: Mimeo: Centro Agronómico Tropical de Investigación y Enseñanza (CATIE). Cartago, Costa Rica. 189 p. https://www.researchgate.net/publication/283491085_Aplicaciones_de_Modelos_Mixtos_en_Agricultura_y_Forestería (30 de septiembre de 2021). [ Links ]
Barrios, A., A. M. López y V. Nieto. 2014. Predicción transición de volúmenes comerciales de Eucalipto grandis a través de modelos de volumen total y de razón. Colombia Forestal 17: 137-149. Doi: 10.14483/udistrital.jour.colomb.for.2014.2.a01. [ Links ]
Beal, S. L. and L. B. Sheiner. 1982. Estimating Population Kinetics. CRC Critical Reviews in Biomedical Engineering 8: 195-222. [ Links ]
Burkhart, H. E. 1977. Cubic-foot volume of Loblolly Pine to any merchantable top limit. Southern Journal of Applied Forestry 1(2): 7-9. https://www.researchgate.net/publication/233704988_Cubic-Foot_Volume_of_Loblolly_Pine_to_Any_Merchantable_Top_Limi (30 de septiembre de 2021). [ Links ]
Carrero, O., M. Jerez, R. Macchiavelli, G. Orlandoni y J. Stock. 2008. Ajuste de curvas de índice de sitio mediante modelos mixtos para plantaciones de Eucalyptus urophylla en Venezuela. Revista Interciencia 33(4): 265-272. https://www.researchgate.net/publication/46406313 (30 de septiembre de 2021). [ Links ]
Castedo, D. F., U. Diéguez A., M. Barrio A., M. Sánchez R. and K. V. Gadow. 2006. A generalized height-diameter model including random components for radiata pine plantations in northwestern Spain. Forest Ecology and Management 229: 202-213. Doi: 10.1016/j.foreco.2006.04.028. [ Links ]
Corral-Rivas, S. y J. J. Návar-Cháidez. 2009. Comparación de técnicas de estimación de volumen fustal total para cinco especies de pino de Durango, México. Revista Chapingo Serie Ciencias Forestales y del Ambiente 15(1): 5-13. http://www.scielo.org.mx/pdf/rcscfa/v15n1/v15n1a1.pdf (30 de septiembre de 2021). [ Links ]
Corral-Rivas, S., J. G. Álvarez-González, F. Crecente-Campo and J. J. Corral-Rivas. 2014. Local and generalized height-diameter models with random parameters for mixed, uneven-aged forests in Northwestern Durango, Mexico. Forest Ecosystems 1: 1-9. https://forestecosyst.springeropen.com/track/pdf/10.1186/2197-5620-1-6.pdf (30 de septiembre de 2021). [ Links ]
Corral R., S., A. M. Silva A. y G. Quiñonez B. 2019. Modelo generalizado no-lineal altura-diámetro con efectos mixtos para siete especies de Pinus en Durango, México. Revista Mexicana de Ciencias Forestales 10(53): 86-117. Doi: 10.1186/2197-5620-1-6. [ Links ]
De los Santos, V., M. 1976. Tablas de volúmenes para montes de la Península de Yucatán. Escuela Nacional de Agricultura. Departamento de Enseñanza, Investigación y Servicio en Bosques. Texcoco de Mora, Edo. de Méx., México. 82 p. [ Links ]
De los Santos P., H. M., M. Montero M. y M. Kanninen. 2006. Curvas dinámicas de crecimiento en altura dominante para Terminalia amazonia (Gmel.) Excell en Costa Rica. Agrociencia 40: 521-532. http://www.colpos.mx/agrocien/Bimestral/2006/jul-ago/art-11.pdf (30 de septiembre de 2021). [ Links ]
Diéguez-Aranda, U., A. Rojo, F. Castedo-Dorado, J. G. Álvarez, M. Barrio-Anta, F. Crecente-Campo, J. M. González G., C. Pérez-Cruzado, R. Rodríguez S., C. A. López-Sánchez, M. Á. Balboa-Murias, J. J. Gorgoso V. y F. Sánchez R. 2009. Herramientas selvícolas para la gestión forestal sostenible en Galicia. Universidad de Santiago de Compostela. Galicia, España. 259 p. https://www.researchgate.net/publication/305443573_Herramientas_selvicolas_para_la_gestion_forestal_sostenible_en_Galicia (30 de septiembre de 2021). [ Links ]
Gallegos, R., A., M. Sánchez D., G. A. González C., L. Román M., E. Hernández A. y A. Mora S. 2012. Diagnóstico del potencial, productividad y manejo de especies nativas maderables tropicales con alto potencial comercial. Guadalajara, Jalisco, México: Universidad de Guadalajara-Centro Universitario de Ciencias Biológicas y Agropecuarias. Guadalajara, Jal., México. 41 p. https://www.itto.int/files/itto_project_db_input/2596/Technical/Capitulo%202%20Diagn%C3%B3stico%20del%20potencial,%20productividad%20y%20manejo%20de%20especies%20nativas%20maderables.pdf (30 de septiembre de 2021). [ Links ]
García C., X., J. Hernández R., A. Hernández R., G. Quiñonez B., J. C. Tamarit U. y G. G. García E. 2017. Predicción del diámetro normal, altura y volumen a partir del diámetro del tocón en especies tropicales. Revista Mexicana de Ciencias Forestales 8(43): 89-116. Doi: 10.29298/rmcf.v8i43.67. [ Links ]
García, M. del C. y C. Rapelli. 2011. Selección de un modelo lineal mixto de niveles múltiples para modelos el crecimiento de la soja. Revista FABICIB 15: 11-22. Doi:10.14409/fabicib.v15i1.877. [ Links ]
García-Espinoza, G. G., O. A. Aguirre-Calderón, G. Quiñonez-Barraza, E. A. Alanís-Rodríguez, H. M. De los Santos-Posadas and J. J. García-Magaña. 2018. Taper and volume systems based on ratio equations for Pinus pseudostrobus Lindley in Mexico. Forests 9(344): 1-14. Doi:10.3390/f9060344. [ Links ]
García-Espinoza, G. G., O. A. Aguirre-Calderón, G. Quiñonez-Barraza, E. Alanís-Rodríguez, M. A. González-Tagle and J. J. García-Magaña. 2019. Global-local and fixed-random parameters to model dominant height growth of Pinus pseudostrobus Lindley. Revista Chapingo Serie Ciencias Forestales y del Ambiente 25(1): 141-156. Doi: 10.5154/r.rchscfa.2018.06.047. [ Links ]
Gómez-García, E., U. Diéguez-Aranda, R. Özçelik, M. Sal-Cando, F. Castedo-Dorado, F. Crecente-Campo, J. J. Corral-Rivas y M. Arias-Rodil. 2016. Desarrollo de una función de perfil mediante modelos mixtos para Pinus sylvestris en Turquía: Selección de parámetros fijos a expandir. Bosque 37(1): 159-167. Doi:10.4067/S0717-92002016000100015. [ Links ]
Herbario CICY. 2010. Flora Digital: Península de Yucatán. https://www.cicy.mx/sitios/flora%20digital/indice_busqueda.php (13 de marzo de 2020). [ Links ]
Hernández-Ramos, J., H. M. De los Santos-Posadas, J. R. Valdéz-Lazalde, J. C. Tamarit-Urias, G. Ángeles-Pérez, A. Hernández-Ramos, B. Méndez-López y A. Peduzzi. 2017. Estimación del volumen comercial en plantaciones de Eucalyptus urophylla con modelos de volumen total y de razón. Agrociencia 51: 561-580. http://www.scielo.org.mx/pdf/agro/v51n5/1405-3195-agro-51-05-00561.pdf (30 de marzo de 2021). [ Links ]
Hernández-Ramos, J., A. Hernández-Ramos, X. García-Cuevas, J. C. Tamarit-Urias, L. Martínez-Ángel y J. J. García-Magaña. 2018a. Ecuaciones de volumen total y de razón para estimar el volumen comercial de Swietenia macrophylla King. Colombia Forestal 21(1): 34-46. Doi:10.14483/2256201X.11965. [ Links ]
Hernández-Ramos, J., A. Hernández R., X. García C., L. Martínez Á., J. C. Tamarit U. y G. G. García E. 2018b. Sistema compatible de ahusamiento-volumen comercial para Swietenia macrophylla King (caoba) en Quintana Roo, México. Madera y Bosques. 24(3): 1-11. Doi: 10.21829/myb.2018.2431441. [ Links ]
Littell, R., G. Milliken, W. Stroup, R. Wolfinger and O. Schabenberger. 2006. SAS for mixed models. SAS Institute Inc. Cary, NC, USA. 795 p. Doi: 10.1111/j.1541-0420.2006.00596_6.x. [ Links ]
López M., J. O., B. Vargas L., O. A. Aguirre C., , C. G. Aguirre C., P. A. Macario M., M. Martínez S. and J. G. Álvarez G. 2019. Compatible taper-volume systems for major tropical species in Mexico. Forestry 00: 1-19. Doi:10.1093/forestry/cpz033. [ Links ]
Martínez G, M. A., V. A. Sánchez y F. J. Faulin. 2006. Bioestadística amigable. Ediciones Díaz de Santos. Barcelona, España. 936 p. [ Links ]
Niño L., G. S., P. A. Ramos M., A. Barrios y A. M. López A. 2018. Modelos compatibles de ahusamiento-volumen para árboles de Gmelina arborea Roxb. en el Alto Magdalena, Colombia. Colombia Forestal 21(2): 174-187. Doi:10.14483/2256201X.12249. [ Links ]
Organización Internacional de Maderas Tropicales (OIMT). 2020. ITTO Lesser used species. http://www.tropicaltimber.info/ (13 de marzo de 2020). [ Links ]
Özçelik, R. and M. Göçeri. 2015. Compatible merchantable stem volume and taper equations for Eucalyptus plantations in the Eastern Mediterranean Region of Turkey. Turkish Journal of Agriculture and Forestry , 39: 851-863. Doi:10.3906/tar-1501-27. [ Links ]
Patiño V., F., J. L. López T. y A. Gómez D. 1994. Selva (Versión 4) Paquete de cómputo para procesar datos de inventarios forestales para especies de la Península de Yucatán. Mérida, Yucatán: Instituto Nacional de Investigaciones Forestales y Agropecuarias. Mérida, Yuc., México. 46 p. [ Links ]
Pece R., M. 1994. Tabla de volumen comercial para Eucalyptus pellita utilizando el método de la razón volumétrica. Quebracho 2: 54-63. https://fcf.unse.edu.ar/archivos/quebracho/q2_07.pdf (30 de septiembre de 2021). [ Links ]
Pinheiro, J. C. and D. M. Bates. 1995. Approximations to the Log-Likelihood Function in the nonlinear mixed-effects model. Journal of Computational and Graphical Statistics 4: 12-35. https://www.jstor.org/stable/1390625?seq=2#metadata_info_tab_contents (30 de septiembre de 2021). [ Links ]
Prodan, M., R. Peters, F. Cox y P. Real. 1997. Mensura Forestal.: Instituto Interamericano de Cooperación para la Agricultura (IICA)/BMZ/GTZ. San José, Costa Rica. 561 p. [ Links ]
Quevedo, A., M. Jerez, A. Y. Moret y O. Noriega. 2010. Ecuaciones de volumen y calidad de forma para Tabebuia rosea (Bertol.) en plantaciones en líneas. Barinas, Venezuela. Revista Forestal Venezolana 54(2): 195-205. http://www.ula.ve/ciencias-forestales-ambientales/indefor/wp-content/uploads/sites/9/2016/11/2010_Quevedo_et_al.pdf (30 de septiembre de 2021). [ Links ]
Quiñonez B., G., Cruz C., F., Vargas L., B. y Hernández, F. J. 2012. Estimación del diámetro, altura y volumen a partir del tocón para especies forestales de Durango. Revista Mexicana de Ciencias Forestales 3(9): 23-39. Doi:10.29298/rmcf.v3i9. [ Links ]
Quiñonez-Barraza, G., H. M. De los Santos-Posadas, J. G. Álvarez-González y A. Velázquez-Martínez. 2014. Sistema compatible de ahusamiento y volumen comercial para las principales especies de Pinus en Durango, México. Agrociencia 48: 553-567. http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1405-31952014000500008 (30 de septiembre de 2021). [ Links ]
Statistical Analysis System (SAS). 2011. SAS/STAT® 9.3 User’s Guide. SAS Institute Inc. Cary, NC, USA. 106 p. [ Links ]
Román M., M. L., A. Mora S. y G. A. González C. 2016. Sistemas agroforestales con especies de importancia maderable y no maderable, en el trópico seco de México. Avances en Investigación Agropecuaria 20(2): 53-72. http://ww.ucol.mx/revaia/portal/pdf/2016/mayo/5.pdf (30 de septiembre de 2021). [ Links ]
Schabenberger, O. and F. Pierce. 2002. Contemporary statistical models for the plant and soil sciences. CRC Press. Boca Raton, FL, USA. 730 p. [ Links ]
Secretaria del Medio Ambiente y Recursos Naturales (Semarnat). 2014. Inventario Estatal Forestal y de Suelos - Quintana Roo 2013. Colección de inventarios estatales forestales y de suelos 2013-2014.: Editorial Prometeo. Guadalajara, Jal., México. 125 p. [ Links ]
Secretaria del Medio Ambiente y Recursos Naturales (Semarnat). 2017. Anuario estadístico de la producción forestal 2016. México, D. F., México. https://www.gob.mx/cms/uploads/attachment/file/282951/2016.pdf (30 de septiembre de 2021). [ Links ]
Seoane, J. 2014. ¿Modelos mixtos (lineales)? Una introducción para el usuario temeroso. Etologuía 24: 15-37. https://pdfslide.net/download/link/modelos-mixtos-lineales-una-introduccion-para-el-etologuia-24-2014 (30 de septiembre de 2021). [ Links ]
Silva G., E., M. A. Nava M., F. J. Hernández y J. G. Colín. 2018. Funciones compatibles de ahusamiento-volumen para tres especies de Pinus en la Unidad de Manejo Forestal 0808 del estado de Chihuahua. Investigación y Ciencia de la Universidad Autónoma de Aguascalientes 26(73): 58-67. Doi:10.33064/iycuaa201873207. [ Links ]
Silva J., A., F. J. Fuentes, H. Georg, A. Gallegos, P. S. Rosa M., M. Flores y J. G. Hernández R. 2011. Industrialización, comercialización y manejo sostenible de diez especies nativas mexicanas.: Universidad de Guadalajara. Centro Universitario de Ciencias Biológicas y Agropecuarias. Guadalajara, Jal., México 37 p. [ Links ]
Spurr, S. H. 1952. Forest inventory. John Wiley and Sons. New York, NY, USA. 472 p. [ Links ]
Tamarit-Urias, J. C., H. M. De los Santos-Posadas, A. Aldrete, J. R. Valdez-Lazalde, H. Ramírez-Maldonado y V. Guerra-De la Cruz. 2014. Ecuaciones dinámicas de índice de sitio para Tectona grandis en Campeche, México. Agrociencia 48(2): 225-238. http://www.scielo.org.mx/pdf/agro/v48n2/v48n2a8.pdf (30 de septiembre de 2021). [ Links ]
Tamarit U., J. C., G. Quiñonez B., C. Ordoñez P. J. C. Monárrez G. y E. Rojas D. 2016. Modelos de ahusamiento para especies de coníferas en Puebla. INIFAP-CIRGOC-Campo Experimental San Martinito. Puebla, Pue., México. Folleto Técnico Núm. 85. 20 p. [ Links ]
Tamarit U., J. C., E. Rojas D., G. Quiñonez B., C. Ordoñez P. y J. C. Monárrez G. 2017. Sistema de cubicación para árboles individuales de Quercus sp. en bosques bajo manejo de Puebla, México. Revista Mexicana de Ciencias Forestales 8(40): 7-26. Doi:10.29298/rmcf.v8i40.37. [ Links ]
Tapia, J. y J. Návar. 2011. Ajuste de modelos de volumen y funciones de ahusamiento para Pinus pseudostrobus Lindl. en bosques de pino de la sierra madre oriental de Nuevo León, México. Foresta Veracruzana 13(2): 19-28. https://www.redalyc.org/pdf/497/49721457004.pdf (30 de septiembre de 2021). [ Links ]
Received: July 02, 2020; Accepted: September 20, 2021











 texto en
texto en 



