Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.5 no.10 León oct. 2013
Ciencias naturales e ingenierías
Formas funcionales del potencial y la densidad electrónica para grafeno delta dopado
Functional forms of the potential and electronic density for the delta-doped graphene problem
Francisco J. López-Rodríguez, Luis M. Gaggero-Sager
Facultad de Ciencias, Universidad Autónoma del Estado de Morelos, México.
Av. Universidad 1001, C. P. 62210, francisco.lopez@uaem.mx.
Recepción: 28-09-2012
Aceptación: 15-01-2013
Resumen
Establecemos las bases para el estudio del efecto de una línea extendida de impurezas sobre una placa de grafeno. Mediante el uso de análisis dimensional y la propuesta de una ecuación de Poisson bidimensional, obtenemos las formas funcionales del potencial y la densidad electrónica de este problema.
Palabras Clave: Grafeno, Análisis Dimensional, Thomas-Fermi, Delta-dopado, Densidad electrónica, Potencial.
Abstract
We establish the basis for the study of the effect of a extended line of impurities on a sheet of graphene. By using dimensional analysis and proposing a two dimensional Poisson equation, we obtain the functional form of the potential and electronic density of the problem.
Key words: Graphene, Dimensional analysis, Thomas-Fermi, Delta-doped, electronic density, Potential.
Introducción
Una membrana bidimensional de átomos de carbono arreglada en una red hexagonal se conoce con el nombre de grafeno [1, 2]. Debido a esta estructura hexagonal las partículas en grafeno se mueven en dos subredes triangulares, que por convención se denominan A y B como se muestra en la Fig (1). Una de las consecuencias de este tipo de tratamiento es que la relación de dispersión del sistema es cónica alrededor de los puntos K y K' de la primera zona de Brillouin. En consecuencia, el grafeno puede describirse por una ecuación de Dirac, siendo el análogo en materia condensada de un sistema de electrodinámica cuántica en (2+1) dimensiones [1,2]. En grafeno los estados propios son espinores, sin embargo en lugar de espín, las componentes del espinor se asocian a la subred donde las partículas cargadas se mueven. Aparte de esta importante característica, existen muchas otras propiedades que hacen al grafeno un material sorprendente. Entre ellas, podemos mencionar su dureza, la que es 200 veces mayor a la del acero [3]. El grafeno, es también un material casi transparente, es decir, permite el paso de casi toda la luz que incide sobre el [4]. Esta peculiaridad ha sido usada en pantallas táctiles [5]. Además, en este material se ha encontrado una fuerte respuesta no lineal a campos electromagnéticos. Este alótropo del carbono toma una señal de entrada de una frecuencia determinada y produce como señal de salida una señal con una frecuencia que es un múltiplo de la original [6, 7]. Por otra parte, existe una característica que hace al grafeno un material muy prometedor para una gran cantidad de aplicaciones electrónicas, esta es su alta movilidad. Con este material los investigadores han alcanzado movilidades de 200 000 cm2 V-1 s-1 suspendiendo una sola capa de grafeno [8]. Sin embargo, cuando el material es colocado en un substrato, las movilidades decrecen [9]. Las movilidades son ahora del orden de 4 X 104 cm2 V-1 s-1 indicando la importancia en la elección del substrato. Estas movilidades son de hecho un orden de magnitud más grandes que las del silicio, donde para el caso de electrones las movilidades están alrededor de 1 400 cm2 V-1 s-1. Aun cuando, como vemos las movilidades del grafeno son grandes, sería muy importante si mayores movilidades pudieran alcanzarse. En este tema de incremento de movilidades, debemos mencionar que hay análisis que han realizado en muestras con dopaje delta 0 y muestran que la movilidad de GaAs, InAs y ZnSe se incrementa [10,16]. De hecho las movilidades se incrementan alrededor de 2.5 pozos en el caso de GaAs dopados con Si [17]. En este artículo nosotros establecemos las bases para el cálculo de la movilidad de grafeno delta dopado. Siguiendo la aproximación de Thomas-Fermi, comenzamos con el problema estadístico de muchas partículas para obtener de manera autoconsistente una expresión analítica del potencial y la densidad electrónica. Además de la aproximación de Thomas-Fermi usamos la técnica del análisis dimensional para obtener las expresiones que buscamos.
Método
Comenzamos con una línea de dopantes sobre la red de grafeno, como se muestra en la "Fig.(2)". De acuerdo con la teoría de Thomas-Fermi el problema puede resolverse escribiendo la función de densidad de energía [18, 19],
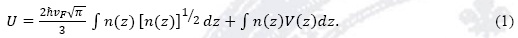

En esta expresión, el primer término corresponde a la energía cinética y el segundo a la energía potencial. En el segundo término se considera la energía potencial debida a las interacciones de Coulomb entre cargas en la red y la debida a la línea de dopantes. En la teoría de Thomas-Fermi, la derivada funcional de U con respecto a la densidad es idéntica al potencial químico
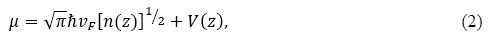
de aquí obtenemos la densidad electrónica

donde

Queremos obtener las expresiones para el potencial efectivo y la densidad electrónica del problema de forma explicita, es decir, como función de la posición. Considerando el caso de otros materiales, como el delta dopado de silicio en GaAs [20]. Problema para el cual conocemos las formas funcionales para el potencial y la densidad electrónica. Podemos suponer que las expresiones para nuestro problema serán muy parecidas a estas, proponemos

entonces usando la Ec.(3)

Usamos ahora análisis dimensional expresamos todas las magnitudes en unidades del radio de Bohr α0 y la constante de Rydberg R0, esto significa


y

En estas expresiones x e y son exponentes que deben ser determinados. Sustituyendo estos parámetros adimensionales en la ecuación para V(z) se sigue

donde Vua(z) = V (z)/R0 y μuα = μ/R0. Observando esta ecuación inmediatamente obtenemos lo siguiente

y

Con estas dos expresiones no es posible determinar los exponentes x e y, que determinarían completamente las expresiones para el potencial y la densidad lineal de dopantes. Para poder hacerlo necesitamos otra relación. Proponemos que las partículas cargadas en nuestro problema satisfacen la siguiente ecuación de Poisson

donde el término con la delta proviene de la línea de impurezas y λ es la densidad lineal de dopantes. El coeficiente c debe ser determinado experimentalmente. Adicionalmente a la escritura de esta ecuación podemos averiguar cuales son las dimensiones de c, haciendo adimensional la ecuación y estudiando el caso z > 0, se tiene


Por lo tanto, c tiene unidades de energía.
Resolvamos la ecuación de Poisson, usando las ecuaciones 5) y 6). Comencemos con la Ec.(5) obtenemos

Usando la Ec.(6) podemos escribir

De aquí vemos que para que la ecuación se satisfaga es necesario que n+2=2n, por lo tanto, n=2. Sustituyendo este resultado en la ecuación anterior encontramos,

y sustituyendo este mismo resultado en las Ecs.(11) y (12) estas quedan de la siguiente manera


vemos entonces que w ≠ 2. Propongamos la elección mas sencilla para ese coeficiente, que es w=3. Con esto hemos determinado los coeficientes necesarios para nuestras funciones V(z) y n(z). Después de haber determinado estos coeficientes, debemos encontrar los otros parámetros de las ecuaciones, esto es, debemos encontrar z0 y α. Es bien conocido que el sistema debe satisfacer electroneutralidad, entonces

donde λ es la densidad lineal de dopantes. Sustituyendo n(z) de las ecuaciones previas tenemos:

Haciendo la integración queda

Sustituyendo los exponentes que encontramos y haciendo todos los parámetros adimensionales, podemos escribir la ecuación anterior como

luego entonces

Para determinar αuα usamos la Ec.(18) con el valor de w = 3. El resultado es,

Habiendo encontrado los parámetros necesarios para determinar las funciones que estabamos buscando, hemos resuelto el problema que nos planteamos en un principio. En los siguientes renglones, escribiremos un resumen de los principales resultados obtenidos.
Obtuvimos que las formas funcionales del potencial y la densidad electrónica del problema son


Estos resultados pueden ser comparados con los resultados para GaAs delta dopado, donde se tiene [20]


con  y n2D es la densidad bidimensional de donadores en la monocapa del delta dopado. La principal diferencia entre el caso de grafeno y el otro, es que el decaimiento como función z para ambas funciones es menor en el caso del alotropo bidimensional del carbono, esto es, la interacción entre cargas es mas intensa, cuando las cargas están mas alejadas, comparadas con el caso de GaAs.
y n2D es la densidad bidimensional de donadores en la monocapa del delta dopado. La principal diferencia entre el caso de grafeno y el otro, es que el decaimiento como función z para ambas funciones es menor en el caso del alotropo bidimensional del carbono, esto es, la interacción entre cargas es mas intensa, cuando las cargas están mas alejadas, comparadas con el caso de GaAs.
Conclusión
Hemos obtenido expresiones cerradas para el potencial y la densidad electrónica para el problema de grafeno delta dopado usando análisis dimensional. Las expresiones encontradas van como el inverso del cuadrado de la distancia, para el caso del potencial y como el inverso de la cuarta potencia de la distancia, para el caso de la densidad electrónica. A partir del presente trabajo se podría determinar y analizar las propiedades de transporte de este sistema (grafeno delta dopado). Sin embargo, eso será el tema de otro artículo.
Agradecimientos
Agradecemos a Isaac Rodríguez Vargas, por resaltar los puntos importantes discutidos en el artículo. Francisco J. López-Rodríguez quiere agradecer la beca otorgada por la Universidad Autónoma del Estado de Morelos a través de Promep.
Referencias
[1] A. H. Castro-Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys. 81, 109 (2009). [ Links ]
[2] A. K. Geim and K. S. Novoselov, Nature Mater. 6, 183 (2007). [ Links ]
[3] C. Lee, S. Wei, J. W. Kysar and J. Hone, Science 321, 385 (2008). [ Links ]
[4] R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science 320, 1308 (2008). [ Links ]
[5] S. Bae, H. Kim,Y. Lee, X. Xu, J.-S. Park,Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim,Y. I. Song, Y.-J. Kim, K. S. Kim, B. Özyilmaz, J.-H. Ah, B. H. Hong and S. Iijima, Nature Nanotechnology 5, 574 (2010). [ Links ]
[6] F. J. López-Rodríguez and G. G. Naumis, Phys. Rev. B 78, 201406(R) (2008). [ Links ]
[7] F. J. López-Rodríguez and G. G. Naumis, Philosophical Magazine 90, 2977 (2010). [ Links ]
[8] K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fuden- berg, J. Hone, P. Klim and H. L. Stormer, Solid State Communications 146, 351 (2008). [ Links ]
[9] J. H. Chen, C. Jang, S. Xiao, M. Ishigami and M. Fuhrer, Nature Nanotech. 3, 206 (2008). [ Links ]
[10] I. Rodríguez-Vargas, L. M. Gaggero-Sager y V. R. Velasco, Surf. Sci. 537, 75 (2003). [ Links ]
[11] I. Rodríguez-Vargas y L. M. Gaggero-Sager, Phys. Status Solidi C 2, 3634 (2005). [ Links ]
[12] L. M. Gaggero-Sager, G. G. Naumis, M. A. Muñoz- Hernandez, V. Montiel-Palma, Physica B 405, 4267 (2010). [ Links ]
[13] I. Rodríguez-Vargas, L. M. Gaggero-Sager y J. C. Martinez-Orozco, Phys. Status Solidi B 242, 1043 (2005). [ Links ]
[14] J.-h. Zhu, D.-w. Gong, Bo Zhang, F. Lu, C. Sheng, H.-h. Sun y X. Wang, Phys. Rev. B 52, 8959 (1995). [ Links ]
[15] Y. Wang, R. J. Hamers y E. Kaxiras, Phys. Rev. Lett. 74, 403 (1995). [ Links ]
[16] W. X. Ni, G. V. Hansson, J. E. Sundgren, L. Hultman, L. R. Wallwenberg, J. Y. Yao, L. C. Markert y J. E. Greene, Phys. Rev. B 46, 7551, (1992). [ Links ]
[17] X. Zheng, T. K. Carns, K. L. Wang, B. Wu, Appl. Phys. Lett. 62, 504 (1993). [ Links ]
[18] L. M. Gaggero-Sager, J. Math. Chem. 25, 317 (1999). [ Links ]
[19] L. Ioriatti, Phys. Rev. B 41, 8340 (1990). [ Links ]
[20] L. M. Gaggero-Sager, Modelling Simul. Mater. Sci. Eng. 9, 1 (2001). [ Links ]














