Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.5 no.10 León oct. 2013
Ciencias naturales e ingenierías
Simultaneous hole scattering in a biased simple barrier
Dispersión simultánea de huecos en una barrera simple
L. Diago-Cisneros1,2 y S. Arias-Laso3
1 Facultad de Física, Universidad de La Habana, Cuba.
2 Departamento de Física y Matemáticas, Universidad Iberoamericana, México D. F.
3 Facultad de Ingeniería Eléctrica, Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba.
S. Arias-Laso. E-mail: sariaslaso@gmail.com. L. Diago-Cisneros. E-mail: ldiago@fisica.uh.cu.
Recepción: 04-05-2012
Aceptación: 12-10-2012
Abstract
A theoretical analysis of the (heavy/light)-hole propagating fluxes through a simple barrier het erostructure of III-V semiconductors is developed considering an external perturbation. We include the interaction with an external electric field parallel to the direction of propagation -normal to the interfaces- in the Multicomponent Scattering Approach and study the relevant magnitudes -transmission, conductance and phase time- of hole quantum transport. This formalism allows us to deal with all propagating channels simultaneously. For the simple barrier system we study the dependence of the conductance with the applied bias through the different hole channels. We also analyze how the increasing of the in-plane momentum κτ affects the results, which provides an idea of how the band-coupling influences the transmission with applied bias. Additionally, a brief study of the phase transmission time curves is carried out as a function of the applied voltage in the heterostructure, fixing different values of the band mixing. Our results are successfully compared with some trends obtained previously in the hole tunneling through semiconductor heterostructures using different approaches to this applied here.
Keywords: Scattering, Hole tunneling, Multicomponent Scattering Approach.
Resumen
Se desarrolla un estudio teórico de la propagación de flujos de huecos (pesados/ligeros) a través de una heteroestructura de barrera simple de materiales semiconductores III-V, considerando una perturbación externa. En los cálculos, usando la Aproximación Dispersiva Multicomponente, se incluyó la interacción con un campo eléctrico externo paralelo a la dirección de propagación -perpendicular a las intercaras - y se estudiaron las magnitudes relevantes del transporte cuántico de huecos - transmisión, conductancia y tiempo de fase. Este formalismo nos permitió considerar simultáneamente todos los canales propagantes. Para el sistema de la barrera simple, se estudió la dependencia de la conductancia con el campo aplicado a través de los diferentes canales de huecos. Igualmente, se analizó cómo el aumento del in-plane momentum κτ afecta los resultados, lo cual nos brinda una idea de cómo el acoplamiento entre bandas influencia la transmisión con un voltaje aplicado. Adicionalmente, fijando diferentes valores de la mezcla interbanda, se hizo un breve estudio del tiempo de transmisión de la fase como función del voltaje aplicado en la heteroestructura. Nuestros resultados fueron exitosamente comparados con algunos comportamientos obtenidos previamente en el tunelaje de huecos a través de heteroestructuras semiconductoras usando diferentes aproximaciones.
Palabras clave: Dispersión, Tunelaje de huecos, Aproximación Dispersiva Multicomponente.
Introduction
Transport-magnitude measurements related with tunneling of quasi-particles through semiconductor heterostructures have an extensive data in the literature. More specifically, the study of transmission properties in low-dimensional systems under external perturbations has played a fundamental role in the design of tunneling devices (Wessel and Altarelli 1989, 17). There is a broad range of experiments and theoretical developments devoted to study inter-band tunneling under external bias (Morifuji and Hamaguchi 1991, 19; Kiledjian et al. 1992, 24; Bertran et al. 1994, 23; Pereyra and Anzaldo-Meneses 2005, 419; de Carvalho et al. 2006, 155317; de Carvalho et al. 2006, 041305; Leo et al. 1990, 11; Dragoman et al. 2008, 1; Ertler and Pötz 2011, 165309). Mathematical treatments based on the k.p model and the transfer matrix formalism are usual to solve this kind of problem when analyzing the influence of an external bias in tunneling properties [11]. Propagation of holes through heterostructures with applied bias has a young history in comparison with other charge carriers, which is expected in some sense, since the study of holes propagation demands more powerful and complex mathematical treatments than other charge carriers without band mixing.
In the last decades, a renewed interest for treating holes as the main charge carriers in resonant tunneling has arose (de Carvalho et al. 2006, 041305; Ertler and Pötz 2011, 165309; Lee and Hu 2001, 7; Dragoman and Dragoman 2003, 10; Diago-Cisneros et al. 2006, 045308). Recently, through semiconducting-polymers experiments was demonstrated the strong influence of holes mobility on the charge carriers density, unifying the hole transport picture in field-effect transistors and light-emitting diodes (Tanase et al. 2003, 21). In addition, attractive findings in structures of graphene offered new insights for the design of electronic and optoelectronic devices based on hole tunneling through structures of graphene (Mak et al. 2009, 256405).
Group delay calculations under applied bias have brought a new interest for the study of low dimensional systems. The response time of several nano-structured devices is directly related with the tunneling time of the leading charge carriers. Due to this fact it is of high urgency the knowledge of the time curves as a function of some parameters of a particular physical system, which can predicts the conduct of a particular device. Tunneling time, particularly for holes, has received great attention since it was shown in experiments with GaAs-AlAs superlattices (Schneider et al. 1989, 14) that resonant tunneling through hole subbands occurs faster than transport due to non-resonant tunneling of electrons, in spite of their mass. Tunneling times in asymmetric quantum structures with applied bias have been explored using experimental and theoretical methods, which include luminescence measurements (Leo et al. 1990, 11; Oberli et al. 1989, 5; Brockman et al. 1991, 24) and novel formalisms where analytical expressions of the delay time were founded to be the threshold for anomalous events like the Hartman premonition (Hartman 1962, 12; Sepkhanov et al. 2009, 245433).
With this report we attempt to study the transmission and phase time for holes tunneling a simple barrier under an external electric field. In Section 2 we explain in detail the applied formalism to include the external perturbation in the Multicomponent Scattering Approach. Section 3 contains the numerical simulations that were carried out and the main results we have obtained. Finally, in Section 4 we arrive to the principal conclusions.
Multicomponent Scattering Approach with applied electric field
We consider the tunneling of holes through a semiconductor barrier of nanometric dimensions (d = 10-20 Å), which is embedded in two volumetric layers of III-V materials. Both layers are properly doped to assure that one of the electrodes provides holes that pass through the barrier. In Figure 1, the heterostructure with applied bias under consideration is presented. As we will be dealing with holes, the energies are considered as positive in the valence band.
Our main purpose is to obtain and analyze physically the transmission magnitudes for holes when an external bias is applied as showed in Figure 1. More specifically, we are interested in studying the behavior of the conductance and the phase time for hole-band tunneling through the GaAs/AlAs heterostructure. Our theoretical model is mainly based in the Kohn-Lüttinger model, and we will deal with the physical magnitudes obtained from the MSA. It is well known, that the MSA connects directly the scattering matrix S, which has a strong correlation with the state vectors transfer matrix Msv, with the envelope wave function and its derivative in a single cell (Diago-Cisneros et al. 2006, 045308; Arias-Laso and Diago-Cisneros 2011, 1730). In order to obtain the transmission magnitudes of a system with the previously mentioned features, the problem to be solved is established as follows.
We calculate the transfer matrix Mfd for the whole cell, which is defined as the heterostructure between the points zL and zR represented in Figure 1. As Mfd(zR,zL,) is the matrix that includes the switch of parameters to the left and right of the barrier and the matrices that relate the state and its derivative both with in the electrodes and inside the barrier, it has the form
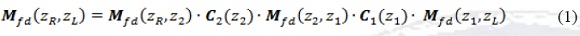
being C1(2)(z1(2)) the matrices that switch the parameters at the points z1(2) respectively. The problem for the wave function vectors between both sides of the barrier, having in mind the definition of the transfer matrix Mfd, stays
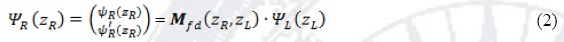
It is useful making use of an expression that relates straightforwardly the propagating state vectors Φ(z) (in both ways) with the envelope wave function Ψ and its derivative Ψ(z)= ℵ • Φ(z) (Diago-Cisneros et al. 2006, 045308; Diago-Cisneros 2006), then we have
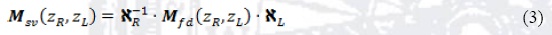
According to (1) and (3), it is evident that obtaining the transfer matrix Mfd is essential in order to study the physical magnitudes we are interested in. In the case of a simple barrier with applied electric field, we need to integrate numerically the KL differential equation system. On the other hand, the form of the matrices ℵR and ℵL is already known, although it is important to mention that with applied electric field, the parameters that characterize both regions L and R do not coincide, because of the electric potential applied to the heterostructure (as one can see in Figure 1).
We are interested in finding the transfer matrix Mfd(z2,z1) corresponding to a region of constant parameters with uniform electric field applied along the direction of propagation. We consider the sub-system up (2x2) of the KL Hamiltonian to find the matrix Mfud (z2Z1), and then we will be able to calculate the transfer matrix of the low sub-system Mfld(z2,z1) and the matrix Mfd(z2,z1) corresponding to the (4x4) space of KL through some well known methods. Afterwards, with expression (3), we can obtain the matrix of interest to calculate the transmission magnitudes.
From the Schrödinger equation corresponding to the sub-system 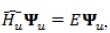 we have
we have
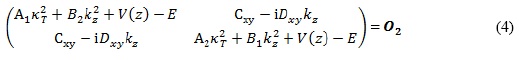
where O2 is the null matrix of second order. The potential corresponding to the physical situation showed in Figure 1 has the form
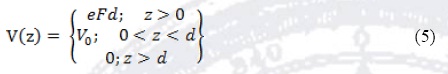
where F represents the applied electric field and e is the modulus of the electron charge. When we write kz = -id/dz in the matrix expression (4), using its matrix form (Garcia-Moliner and Velasco 1992), we obtain
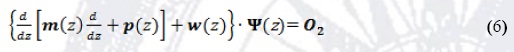
Here we have assumed the matrices p(z) y y are antihermithic, and with constant parameters.
It is usual, when solving numerically a second or higher order differential equation system, to intend to simplify it obtaining an equivalent first order system with a number of equations that agrees with the highest order derivative of the original system. This can be useful since the integration, as a problem of initial values, is straightforward when one consider the first order system and the implemented methods to solve this system are better optimized. We now need to turn the system (6) in the form

At this point, it would be useful to define the vector 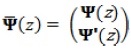 , which converts the N-equation system (6) into a 2N-differential equation system of first order. From Equation (6), the first derivative of the proposed vector can be expressed as
, which converts the N-equation system (6) into a 2N-differential equation system of first order. From Equation (6), the first derivative of the proposed vector can be expressed as
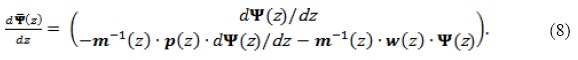
This last expression is equivalent to write
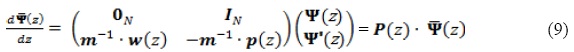
Solution of Equation (9) is straightforward and has the form
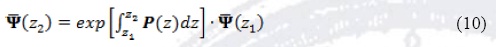
As one can notice, Equation (10) contains the definition of the function and derivative transfer matrix Mfd(z2z1). The problem to be solved has three regions: L, barrier and R. In regions L(R) the full transfer matrix can be obtained in a similar way as in the case without electric field (Diago-Cisneros et al. 2006, 045308; Arias-Laso and Diago-Cisneros 2011, 1730; Diago-Cisneros 2006), although it is important to take into account there is a difference of potential between regions L and R, so the transfer matrix will differ for given fixed energies and κτ. On the other hand, we apply the definition of canonical basis for the barrier region, as one in which the TM of function and derivative is the identity matrix, then we solve Equation (9) after apply repeatedly, with a set of values for the energy and κτ, the initial vectors (Press et al. 1997)
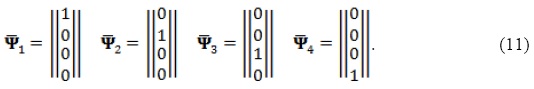
The expression obtained for Mfd(z2,z1) must be conveniently multiplied by (1) and then, by Equation (3), be used in order to study the transmission properties of the heterostructure in resemblance with the usual mechanism without applied external bias (Diago-Cisneros 2006). We are concerned in calculating the transmission probabilities and the conductance of the system, in addition with the phase transmission time for hole bands. If we consider the incoming particles from the left, the transmission probability from the j channel to the i channel is defined by

where tij represent the transmission amplitudes for the incoming particles given by the definition of the transfer matrix Msv and the direct relation that connects this matrix with the scattering matrix S.
The two-probe Landauer conductance will be obtained as follows

and finally, the phase transmission time is calculated based on the expression

where Φij stands for the phase-transmission amplitudes, which are directly related with the complex transmission amplitudes (Diago-Cisneros et al. 2006, 045308; Arias-Laso and Diago-Cisneros 2011, 1730; Diago-Cisneros 2006).
Numerical Results
The sketched scheme in Figure 1 shows the hole transport process we intend to study. For the simple barrier system the following parameters were fixed: a barrier/well width (Lb/Lw) of 30/50 Å, and a barrier height (Vb) of 0.55 eV. On the other hand, the energy of the electric field was varied within the range of [0-6x10-4] eV and the incoming-flux energy was fixed at Ei = 0.02 eV. In order to see how band mixing affects the results the value of κτ was varied in the interval of [10-4-10-2] Å-1.
Transmission of holes with different band mixing
Figure 2 exhibits the conductance dependences with the applied voltage as the band mixing is increased from 10-4Å-1 to 10-2Å-1. As one can see, when mixing between the propagating modes is too low (panels 2(a) and 2(d)) the scattering channels are uncoupled. For this reason, it is expected the predominance of transmission probabilities corresponding to direct transitions over the ones from crossed transitions. Therefore, in every curve of conductance in Figure 2 the principal component is the one corresponding to the direct transition. Nevertheless, even for this small value of κτ, there are some crossed paths that remain open, which leads to obtain some non-zero transmission probabilities for crossed transitions. This behavior is a direct consequence from the breaking of the time reversal invariance symmetry in the (4x4) dimension due to the electric bias effects. Another remarkable feature in this figure is the more powerful influence of the light holes in comparison with the heavy holes, independently of the voltage values. This last trend was already found in a study of the inter-band tunneling of holes through a similar heterostructure (Morifuji and Hamaguchi 1991, 19).
As the inter-band tunneling is reinforced, one can notice that the transmission through the open channels decreases remarkably. This is the situation presented by the panels 2(b), 2(c), 2(e) and 2(f) of Figure 2. These sub-figures show the conductance as a function of the applied voltage given fixed κτ=10-3Å-1 and κτ= 10-2Å-1. This vanishing in the transmission occurs when hole mixing is increased because of some paths, that were previously forbidden, start to be opened for tunneling. Even for these high values of band mixing, light holes conduction remains dominant in comparison with heavy holes.
The MSA formalism allows us to study in detail the crossed transitions, then in Figure 3 we refer to the transmission probabilities for three crossed paths - hh+3/2→ lh+1/2, lh-1/2 → lh+1/2 and lh-1/2 → hh-3/2 - as a function of the applied voltage respectively. The curves corresponding to the same magnitudes are also shown when the in-plane quasi-momentum is increased in one order of magnitude. These trends are exhibited in order to illustrate the openingn of new crossed-propagating channels when the band mixing is increased from κτ= 10-3Å-1 to κτ=10-2Å-1. As one can see from panel 3(a), crossed transition hh+3/2 → lh+1/2 was forbidden for κτ = 10-3 Å-1 where the hole tunneling tended to be mostly uncoupled, but as κτ is increased the probability of tunneling through this crossed path starts to grow, even for small values of the order of 10_15. A similar trend is observed for the other two crossed transitions in panels 3(b) and 3(c). In this case, the electric field induces the inter-band mixing, even for small values of κτ where the crossed paths should be closed.
In Figure 4 the two-probe Landauer conductance for the simple-barrier system is exhibited in dependence with the applied voltage for different values of κτ. It is clear that the transmission of the system falls rapidly with the increasing of the band mixing. This behavior evidences the significant effect of the band mixing over the volt-amperic (V-I) curve, as was reported in theoretical studies for the double barrier resonant tunneling (DBRT) (Rosseau et al. 1989). Even though we do not show here V-I curves strictly speaking, it is still valid to analyze the conductance, since this global magnitude is related straightforwardly with the tunneling-density current (Landauer and Martin 1994, 1). Figure 4 shows clear evidences that for a fixed incoming energy, the rising of the applied voltage above 25 mV practically closes the whole transmission. In this case, the incident energy was fixed at 0.02 eV and as the electric field energy increases, this magnitude can reach a value for which the propagating states in the L region (see Figure 1) remain in the forbidden energy range which provokes the transmission to vanish (Diago-Cisneros 2006).
Phase Transmission Time
Figure 5 presents the phase transmission time for hole-propagating channels through the simple barrier with applied electric field. Sub-figures 5(a), 5(b) and 5(c) shows the phase time dependences with the applied voltage for different values of the band mixing. When κτ = 10-4Å-1 the channels mixing is practically null and the phase time for the direct transitions is dominant. One can notice from panel 5(a) there is a degeneracy among the curves depending on the effective mass. The phase times for direct transitions hh±3/2 → hh±3/2 (dotted red line) and lh±1/2 → lh±1/2 (dotted purple line) are degenerated in spin-up and spin-down respectively. This behavior is caused for the low mixing between hole bands, in this case hole channels are uncoupled and the phase time of a transition from one state to another with the same effective mass and certain spin polarization matches with the transition corresponding to the opposite spin polarization. It is easy to notice the breaking of this degeneracy in panel 5(b), which means that for a greater mixing the hole channels are not uncoupled anymore and previously forbidden crossed paths start to be opened for tunneling. For a strong mixing, κτ = 10-2Å-1, the phase time shows trends noticeably different than the previous ones, even appearing negatives values of this magnitude. As one can see in panel 5(c), phase time curves corresponding to heavy holes, as to light holes, show a symmetric behavior with reference to τ = 0. This trend demands a more deep study to figure out whether is caused for numerical reasons or have an explanation from the physical point of view.
Conclusions
A theoretical study of the hole tunneling through a simple barrier with applied electric bias was carried out by including the effects of the external perturbation in the Multicomponent Scattering Approach. The conductance for direct transitions of light holes evidences a dominant behavior over the heavy holes, independently of the applied voltage and κτ. Crossed transitions for a low band mixing are a clear evidence of the inter-subband mixing effect of the electric field even for κτ=10-4Å-1 As the coupling between channels increases, the transmission of the system vanishes rapidly, showing the strong influence of the mixing on the V-I curves of the system. In the phase time results it is noticeable the existence of a degeneracy when the hole bands are uncoupled and the breaking of this trend with the rising of κτ. The limit case of strong coupling, exhibits a symmetric splitting of the time curves around a mean value, even surrounding negative values of the phase time. This last behavior requires a more carefully treatment to understand the physics behind the results.
References
Wessel, R. and Altarelli, M. (1989). Resonant tunneling of holes in double-barriers heterostructures in the envelope function approximation. Phys. Rev. B, 39: 17-23. [ Links ]
Morifuji, M. and Hamaguchi, C. (1991) Theoretical study on interband tunneling of holes through GaAs/AlAs/GaAs single-barrier heterostructures. Phys. Rev. B, 52: 19-25. [ Links ]
Kiledjian, M. S., Schulman, J. N. , Wang, K. L. and Rousseau, K. V. (1992). Interband resonant tunneling in InAs/AlSb/GaSb symmetric polytype structures. Phys. Rev. B, 46: 24-30. [ Links ]
Bertram, D., Grahn, H. T., Van Hoof, C., Genoe, J., Borghs, G., Rühle, W. W. and von Klitzing, K. (1994). Time-resolved photoluminiscence spectroscopy of resonant tunneling in a GaAs/AlAs triple-barrier structure. Phys. Rev. B, 50: 23-30. [ Links ]
Pereyra, P. and Anzaldo-Meneses, A. (2005). Electronic transport and interfering phenomena induced by transverse electric field. Microelectron. J., 36: 419-422. [ Links ]
de Carvalho, H. B., Galvão Gobato, Y., Brasil, M. J. S. P., Lopez-Richard, V., Marques, G. E., Camps, I., Henini, M., Eaves, L. and Hill, G. Voltage-controlled hole spin injection in nonmagnetic GaAs/AlAs resonant tunneling structures. Phys. Rev. B, 73: 155317-155326. [ Links ]
de Carbalho, H. B., Brasil, M. J. S. P., Lopez-Richard, V., Galvão Gobato, Y., Marques, G. E., Camps, I., Dacal, L. C. O., Henini, M., Eaves, L. and Hill, G. (2006). Electric-field inversion asymmetry: Rashba and stark effects for holes in resonant tunneling devices. Phys. Rev. B, 74: 041305-041309. [ Links ]
Leo, Karl, Shah, Jagdeep, Gordon, J. P., Damen, T. C., Miller, D. A. B., Tu, C. W. and Cunningham, J. E. (1990). Effect of collisions and relaxation on coherent resonant tunneling: I Hole tunneling in GaAs/AlxGa1-xAs double-quantum-well structures. Phys. Rev. B, 42: 11-15. [ Links ]
Dragoman, D., Dragoman, M. and Müller, A. A. (2008). Graphene -a one-atom-thick material for microwave devices. Romanian Journal of Information Science and Technology, 11: 1-7. [ Links ]
Ertler, Christian and Pötz, Walter. (2011). Electrical control of ferromagnetism and bias anomaly in mn-doped semiconductor heterostructures. Phys. Rev. B, 84: 165309-165319. [ Links ]
Lapushkin, I., Zakharova, A., Gergel, V., Goronkin, H. and Tehrani, S. Self-consistent modeling of the current-voltage characteristics of resonant tunneling structures with type ii heterojunctions. J. Appl. Phys., 82: 5-11. [ Links ]
Lee, Wen-Chin and Hu, Chenming. (2001). Modeling CMOS tunneling currents through ultrathin gate oxide due to conduction- and valence-band electron and hole tunneling. IEEE T. Electron. Dev., 48: 7-15. [ Links ]
Dragoman, Daniela and Dragoman, Mircea. (2003). Single-chip device for tunneling time measurements. J.Appl. Phys., 93: 10-14. [ Links ]
Diago-Cisneros, L., Rodriguez-Coppola, H., Pérez-Alvarez, R. and Pereyra, P. (2006). Multichannel tunneling in multiband heterostructures: Heavy-hole and light-hole transmission properties. Phys. Rev. B, 74: 045308-045320. [ Links ]
Tanase, C., Meijer, E. J., Blom, P.W. M. and de Leeuw, D. M. (2003). Unification of the hole transport in polymeric field-effect transistors and light-emitting diodes. Phys. Rev. Lett., 91: 21-25. [ Links ]
Mak, Kin Fai, Lui, Chun Hung, Shan, Jie and Heinz, Tony F. (2009). Observation of an electricfield-induced band gap in bilayer graphene by infrared spectroscopy. Phys. Rev. Lett., 102: 256405-25409. [ Links ]
Schneider, H., Grahn, H. T., Klitzing, K. and Ploog, K. (1989). Sequential resonant tunneling of holes in GaAs/AlAs superlattices. Phys. Rev. B, 40: 14-18. [ Links ]
Oberli, D. Y., Shah, J., Damen, T. C., Tu, C. W., Zhang, T. Y., Miller, D. A. B., Henry, J. E., Kopf, R. F., Sauer, N. and DiGiovanni, A. E. (1989). Direct measurements of resonant and nonresonant tunneling times in asymmetric coupled quantum wells. Phys. Rev. B, 40: 5-9. [ Links ]
Brockmann, P., Young, Jeff. F., Wasilewski, Z. and Buchanan, M. (1991). Influence of scattering on the resonant transfer of holes between two-dimensional states. Phys. Rev. B, 44: 24-28. [ Links ]
Hartman, T. E. (1962). Tunneling of a wave packet. J. Appl. Phys., 33: 12-19. [ Links ]
Sepkhanov, R. A., Medvedyeva, M. V. and Beenakker, C. W. J. (2009). Hartman effect and spin precession in graphene. Phys. Rev. B, 80: 245433-245438. [ Links ]
Arias-Laso, S. and Diago-Cisneros, L. (2011). Giant conductance and phase time anomalous events of hole quantum transport. Physica E, 44: 1730-1741. [ Links ]
Diago-Cisneros, L. (2006). Tunelaje multicanal y simetría de los huecos en heteroestructuras semiconductoras. Universidad de La Habana, Cuba. [ Links ]
García-Moliner, F. and Velasco, V. R. (1992). Theory of Single and Multiple Interfaces. World Scientific, Singapore. [ Links ]
Press, W. H., Teukolsky, S. A., Vetterling, W. T. and Flannery, B. P. (1997). Numerical Recipes. University of Cambridge. [ Links ]
Rosseau, K. V., Wang, K. L. and Schulman, J. N. (1989). Resonant tunneling of holes in single and double barrier GaAs/AIGaAs structures. Superlattice. Microst., 67: 1-7. [ Links ]
Landauer, R. and Martin, Th. (1994). Barrier interaction time in tunneling. Rev. Mod. Phys., 66: 1-13. [ Links ]














