Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.5 no.9 León abr. 2013
Ciencias naturales e ingenierías
Una ecuación para ondas en un fluido rotatorio que se desplaza con movimiento helicoidal a lo largo del eje de rotación
An equation for waves in a fluid moving with rotating helical motion along the axis of rotation
José Marín Antuña1
1 Departamento de Física Teórica, Facultad de Física, Universidad de La Habana, Cuba.
José Marín Antuña. E-mail: marin@fisica.uh.cu.
Recepción: 26-04-2012
Aceptación: 06-08-2012
Resumen
Para posibles aplicaciones en el estudio teórico de procesos ondulatorios en diferentes tipos de dispositivos de aplicaciones técnicas importantes, y también desde el punto de vista puramente físico y matemático, desarrollamos un modelo para describir pequeñas oscilaciones acústicas en un fluido rotatorio con un movimiento helicoidal a lo largo del eje de rotación. Se obtiene una ecuación no clásica de cuarto orden en derivadas parciales para describir tales movimientos. Se estudian algunos casos particulares y estos se comparan con ecuaciones obtenidas en artículos anteriores.
Palabras clave: Fluido rotatorio, movimiento helicoidal, eje de rotación, oscilaciones acústicas.
Abstract
For possible applications in the theoretical study of wave processes in different kind of devices of important technical applications, and also from the pure physical and mathematical point of view, we develop a model to describe small acoustic oscillations in a rotating fluid with a helicoidal movement along the rotating axis. A non classical fourth order partial differential equation is obtained to describe such movements. We study some particular cases and compare this cases with equations obtained in previous papers.
Keywords: Rotating fluid, helicoidal movement, rotating axis, acoustic oscillations.
Introducción
En el estudio de los procesos físicos en medios de diferente naturaleza tiene importancia básica el estudio de los procesos de generación de ondas acústicas originadas por perturbaciones de diferente tipo. Esas perturbaciones pueden estar ocasionadas por pulsaciones, ruidos y otras causas. Las ondas así generadas pueden entrar en resonancia con los parámetros del sistema donde se generan, lo que podría ocasionar diferentes tipos de problemas. El presente trabajo desarrolla una generalización de resultados anteriores en el tema de ondas en fluidos rotatorios. Desde hace tiempo diversos autores han tratado de modelar el proceso de la generación y propagación de ondas en sistemas similares [1,2]. Aportes sustanciales al tema provienen desde la época del trabajo fundamental [3], que fundó toda una escuela en la antigua Unión Soviética [4,5,14]. El autor del presente trabajo ha hecho aportes al tema en diversas publicaciones [6,7,8,9]. Un enorme trabajo ha sido dedicado al tema de fluidos rotatorios y la literatura al respecto es amplísima, por su interés para la modelación de procesos geofísicos de la atmósfera y el océano mundial, así como en la modelación de estrellas; ver, por ejemplo, los artículos [10,11,12,13]. Igualmente, no pocas monografías han sido dedicadas al tema [15,16,18].
Desde el punto de vista estrictamente físico matemático, las ecuaciones que describen estos procesos resultan de gran interés y ello constituye el cuerpo central del presente trabajo. Las ecuaciones que aquí presentamos se reducen a las obtenidas en [9], lo que valida la autenticidad de los cálculos realizados. El trabajo tiene un carácter inicial en el estudio del tema de las ondas en fluidos con avance helicoidal, lo que significa que posteriormente se continuará en su desarrollo con la intención de resolver problemas de búsqueda de soluciones fundamentales del operador hallado, así como la obtención de autovalores y autofunciones en estructuras cilíndricas con gases rotando en su interior y avanzando helicoidalmente a lo largo del eje de rotación.
Consideremos los procesos ondulatorios inicialmente en un fluido ideal incompresible que rota con velocidad angular constante Ω=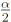 (a es el parámetro de Coriolis) y que, además, se mueve como un todo con velocidad constante de magnitud β a lo largo del eje de rotación, realizando un movimiento helicoidal. En ausencia de perturbaciones ondulatorias cada partícula de fluido se mueve por una espiral, realizando un movimiento de avance en espiral con paso
(a es el parámetro de Coriolis) y que, además, se mueve como un todo con velocidad constante de magnitud β a lo largo del eje de rotación, realizando un movimiento helicoidal. En ausencia de perturbaciones ondulatorias cada partícula de fluido se mueve por una espiral, realizando un movimiento de avance en espiral con paso 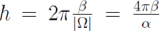 y radio igual a la distancia de la partícula al eje de rotación. Tales movimientos serán llamados "flujos helicoidales".
y radio igual a la distancia de la partícula al eje de rotación. Tales movimientos serán llamados "flujos helicoidales".
Ecuación de ondas en el flujo helicoidal en un fluido rotatorio incompresible
Veamos flujos helicoidales de un fluido ideal homogéneo incompresible respecto a un sistema de coordenadas cartesianas que rota junto con el fluido, de forma tal que el eje está dirigido a lo largo del eje de rotación. Entonces, con respecto a este sistema de coordenadas cartesianas (x1, x2, x3), las partículas del fluido se moverán en la dirección del eje Ox3 de rotación con velocidad de flujo 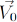 =(0, 0, β). El sistema de ecuaciones de la hidrodinámica del fluido rotatorio, linealizado con respecto al flujo estacionario con velocidad
=(0, 0, β). El sistema de ecuaciones de la hidrodinámica del fluido rotatorio, linealizado con respecto al flujo estacionario con velocidad 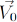 tiene la forma
tiene la forma

donde 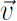 es el vector de perturbaciones de la velocidad de las partículas del fluido. (Aclaremos que la velocidad total de las partículas de fluido respecto al sistema de coordenadas elegido es
es el vector de perturbaciones de la velocidad de las partículas del fluido. (Aclaremos que la velocidad total de las partículas de fluido respecto al sistema de coordenadas elegido es 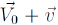 y, al realizar la linealización, suponemos que
y, al realizar la linealización, suponemos que  es la presión dinámica,
es la presión dinámica,  = (0, 0, α) es el vector de Coriolis. Al escribir (1) hemos supuesto que la densidad del fluido es igual a 1.
= (0, 0, α) es el vector de Coriolis. Al escribir (1) hemos supuesto que la densidad del fluido es igual a 1.
Al escribir por componentes (1) obtenemos:

Mediante un proceso de derivación y sustitución de las ecuaciones, no es difícil llegar a que tanto la presión dinámica, como cada una de las componentes de las velocidades de las partículas del fluido satisfacen la ecuación:

donde 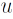 puede ser la presión dinámica p o cada una de las componentes del vector
puede ser la presión dinámica p o cada una de las componentes del vector 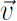 .
.
Esta ecuación se conoce con el nombre de ecuación de las ondas lineales en un flujo helicoidal en fluidos incompresibles ([16],[17]). Para ella fueron estudiados los problemas de frontera, así como los regímenes estabilizados.
Sin embargo, para los fluidos compresibles, no se ha realizado hasta el momento ningún estudio sistemático de estos flujos helicoidales, lo que haremos a continuación para la propagación de ondas acústicas.
Ecuación de ondas en el flujo helicoidal en un fluido rotatorio compresible
Al considerar compresible el fluido, la ecuación de continuidad cambia, de manera que el sistema (1) ya linealizado e isentrópico (ver condiciones para ello en [9]) es

donde c tiene el sentido físico de la velocidad del sonido en el fluido. Este sistema escrito explícitamente por coordenadas es (sin perder generalidad consideraremos movimientos bidimensionales, entendidos como aquellos en los que 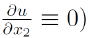 .
.

En aras de obtener una ecuación de orden superior equivalente a este sistema, apliquemos a (α') el

Entonces obtenemos:
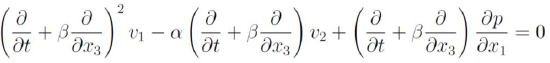
Pero, de acuerdo con (b'):

Por lo que nos queda:
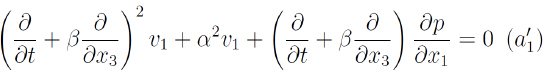
Apliquemos tres veces el operador (6) a (d):
y coloquemos
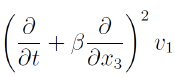
de (α'1). Queda:

Ahora, a (c') le aplicamos:
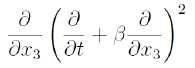
y queda:

Colocando esta expresión en (7) obtenemos:

Ahora bien, de (d') tenemos que:

Por lo que, al colocar esto en (8) obtenemos:
Pero de (c')

de manera que, finalmente obtenemos la ecuación diferencial no clásica de cuarto orden que describe las oscilaciones acústicas en un fluido rotatorio compresible que realiza un movimiento helicoidal a lo largo del eje de rotación:

Como se aprecia, el límite incompresible (c → ∞) en esta ecuación nos da la ecuación (3) antes mencionada.
Además, si consideramos el movimiento rotatorio, pero sin avance helicoidal (o sea, β = 0), la ecuación (10) se reduce, como un caso particular, a la ecuación obtenida en [9]:
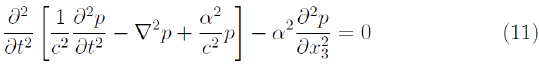
que, si consideramos, además, el movimiento sin rotación, nos da la ecuación hiperbólica clásica de una onda:

Es conveniente señalar que la ecuación (10) y su caso particular (11) son ecuaciones no clásicas de cuarto orden en el tiempo. El planteamiento matemático del problema de Cauchy para tales ecuaciones requiere que se impongan los valores iniciales de la función solución y de sus derivadas temporales hasta el tercer orden. Las condiciones iniciales arriba mencionadas se interpretan como la igualdad a cero en el momento inicial de la función buscada, de su velocidad, W. de su aceleración y de la variación de dicha aceleración. De ser diferentes de cero, como se sabe, siempre se puede proponer la solución por el método de superposición de forma que dichas condiciones iniciales se reduzcan a cero [14]. Aunque poco comunes, en la física existen situaciones donde aparece la tercera derivada de la solución de determinados problemas; por ejemplo el relacionado con la radiación de ondas electromagnéticas [19]. En trabajos anteriores [4,5,6] se demostró un teorema de unicidad para tales problemas, la existencia de diferentes tipos de ondas que pueden generarse en dichos fluidos y su difracción en diferentes obstáculos sumergidos en dichos medios.
Conclusiones
Los cálculos realizados muestran una generalización de las ecuaciones físico matemáticas que describen ondas acústicas en los fluidos considerados. Debido a la complejidad matemática de dichas ecuaciones es necesario continuar su estudio mediante la búsqueda de relaciones de dispersión y soluciones fundamentales que permitan acometer problemas diversos relacionados con la propagación reflexión y difracción de este tipo de ondas en tales medios. Dicha tarea está en estos momentos en progreso.
Referencias
[1] J.B. Morton and E.J. Shaughnessy, "Waves in a gas in solid-body rotation'', J. Fluid Mech. (1972), 56, 2, 277-286. [ Links ]
[2] John W. Miles, "Waves in a rapidly rotating gas'', J. Fluid Mech. (1981), 107, 487-497. [ Links ]
[3] S.L. Soboliev, "Sobre un nuevo problema de la Física Matemática (en ruso)'', Izv. AN SSSR serie matem.(1954)18, 1, 3-50. [ Links ]
[4] V.N. Masliennikova, "Problemas matemáticos de la hidrodinámica en un fluido rotatorio y sistemas de Soboliev (en ruso)'', Disertación de Doctor en Ciencias, Novosibirsk. (1971). [ Links ]
[5] S.A. Gabov, "Espectro y bases de autofunciones de un problema de oscilaciones acústicas en un fluido rotatorio (en ruso)'', Dokl. AN SSSR (1980), 254, 4, 777-779. [ Links ]
[6] S.A. Gabov, J. Marín-Antuña, "On a non-stationary problem for waves diffraction in a rotating compressible liquid'', Moscow University News, series 3, MSU, (1985), 26-3, 16-20. [ Links ]
[7] J. Marín-Antuña, "Ondas planas de amplitud variable en líquidos rotatorios compresibles. Problema de autovalores'', Rev. Cub. Fis. (1992), 12, 3, 214-219. [ Links ]
[8] J. Marín-Antuña, "Difraction of a step-like wave on a wall of longitude h in a compressible rotating fluid", Rev. Cub. Fis. (2002), 19, 1, 23-25. [ Links ]
[9] J. Marín-Antuña, R.L. Hall, N. Saad "Wave equation and dispersion relations for a compressible rotating fluid'', Physics Letters A (2007), 362, 57 - 60. [ Links ]
[10] Y.D. Chashechkin. International Conference on Boundary and Interior Layers, BAIL 2004, Tolouse, France, July 2004. [ Links ]
[11] K. Zhang, C.A. Jones, Geophys. Res. Lett. (1994) 24, 1939. [ Links ]
[12] S.J. Friedlander, J. Geophys. J. R. Astron. Soc. (1987) 89, 637. [ Links ]
[13] J. Marín-Antuña, A. Hernández-Rodríguez, O. Sotolongo Costa, "An equation for waves in a viscous rotating compressible fluid", in: Proc. DFD, APS, November 1995. [ Links ]
[14] S.A. Gabov, A.G. Sveshnikov, A.K. Shatov, Dokl. Akad. Nauk SSSR (1983) 268, 1095. [ Links ]
[15] L.M. Brekhovskikh, V. Goncharov, Mechanics of Continua and Wave Dynamics, second ed., Springer Series on Wave Phenomena, vol. 1, Springer- Verlag, New York, 1994. [ Links ]
[16] G.B. Whitham, Linear and Nonlinear Waves, Wiley, New York, 1999. [ Links ]
[17] S.A. Gabov. Nuevos Problemas de la Teoría de Ondas (en ruso), Moscú, Editorial Nauka, 1998. [ Links ]
[18] L.D. Landau, E.M. Lifshitz, Fluid Mechanics, second ed., Pergamon Press, 1987. [ Links ]
[19] L.D. Landau, E.M. Lifshitz, The Classical Theory of Fields. fourth revised ed., Pergamon Press, 1975. [ Links ]
















