Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.4 no.8 León oct. 2012
Ciencias naturales e ingenierías
Radioterapia y el papel del sistema inmunitario
Radiotherapy and the role of the immune system
Oscar Sotolongo Grau1, Daniel Rodriguez Pérez 1, J. C. Antoranz 1, 3, Luis M. Gaggero Sager2 y Oscar Sotolongo Costa3
1 Departamento de Física Matemática y Fluidos, Universidad Nacional de Educación a Distancia, Madrid, España.
2 Departamento de Física, Universidad Autónoma del Estado de Morelos, Cuernavaca., México.
3 Cátedra de Sistemas Complejos "Henri Poincaré" Universidad de La Habana, La Habana., Cuba.
Oscar Sotolongo. Cátedra de Sistemas Complejos "Henri Poincaré" Universidad de La Habana., Cuba. E-mail: osotolongo@fisica.uh.cu
Recepción: 23-01-2012
Aceptación: 26-03-2012
Resumen
Se simuló computacionalmente un gran número de pacientes bajo tratamiento de radioterapia, mediante un sistema dinámico. De los resultados, se halló un método para cambiar el número de sesiones de radiación manteniendo óptimo el tratamiento. Además, se obtuvo que la relación entre la fracción sistema inmune-eficiencia tumoral para un paciente dado y la máxima probabilidad de éxito del tratamiento sigue una ley de potencias.
Palabras clave: Sistemas Dinámicos, Radiobiología.
Abstract
Using a population dynamics formulation to model radiotherapy treatments a large amount of patients under treatment was mimicked. From the obtained results a method to change the number of radiation sessions while keeping the optimized treatment is found. Also a power law relating immune system - tumor efficiency ratio (ISTER) for a given patient and maximum success probability of radiotherapy treatment is obtained.
Key words: Dynamical Systems, Radiobiology.
1 Introduction
The relevance of immune system tumor interaction in a radiotherapy treatment (RT) and the importance of its study have been highlighted in a previous work [1]. The role of immune system in tumor control has been described in [2] and widely discussed in further works [3-8]. However, in our opinion, the need of its study and characterization to plan a treatment has not been fully understood.
Mathematical models are widely used to describe tumoral behaviour withor without treatment. Such models have been used to explain and to describe immune depression effects [9], the role of time delays in immune response [10, 11], radiovirotherapy treatments [12], chemotherapy treatments [13] and even surgery [14].
There is an increasing concern about finding the suitable planning that maximizes the outcome of a radiotherapy (RT) treatment [15]. Generally speaking, the problem of how to apply radiation treatments in an optimal way taking into account the influence of external factors is, in our opinion, far from being fully solved, specially in what concerns the derivation of general decision tools to organize and adopt radiotherapy protocols in actual clinical conditions.
In the present work we investigate how to apply the optimum dosage and to adapt this optimal treatment to other protocols with a different number of sessions. This could be useful to oncology services to plan the RT treatments without decreasing treatment performance. Also the oncologists could adjust the radiation dosage in order to minimize the damage caused to the surrounding tissue.
2 Modeling radiotherapy
2.1 Model
We will use a Lotka-Volterra like model to describe the tumor evolution based on some assumptions. Tumor cells growth ![]() (as usual, a dot over a quantity represents its time derivative) depends on the current tumor population as aX and its interaction with lymphocytes, -bXY . Lymphocyte population grows due to tumor-immune system interaction, dXY , and contribution to exponential decay, -fY , due to natural cell death. The tumor is assumed to secrete interleukin which produces an immunity depression effect [16, 17], -kX. In this model a constant flow, u, of lymphocytes arrives from the immune system.
(as usual, a dot over a quantity represents its time derivative) depends on the current tumor population as aX and its interaction with lymphocytes, -bXY . Lymphocyte population grows due to tumor-immune system interaction, dXY , and contribution to exponential decay, -fY , due to natural cell death. The tumor is assumed to secrete interleukin which produces an immunity depression effect [16, 17], -kX. In this model a constant flow, u, of lymphocytes arrives from the immune system.
So, we model tumor-immune system interaction using the already known equations [9]:

as a result of RT treatment a fraction of cells of both populations, lymphocytes and tumor cells are affected. The lymphocytes population get quickly reduced in a fraction Bl of cells in what is called the interphase death. However, affected tumor cells will not die immediately but a fraction Bt loses its reproductive capacity and dies in the mitosis process. The fraction of affected cells in both populations is the complement of the survival factors St,1 = 1-Bt,1.
The inclusion of both populations affection brings a new equation for the tumor non clonogenic cells [12], Z, originated from radiation damage. We assume that those cells will also stimulate the lymphocytes population, as pZY , will decay exponentially as -rZ due to the death of damaged cells, and as -qZY due to the interaction with immune system. Finally we arrive to
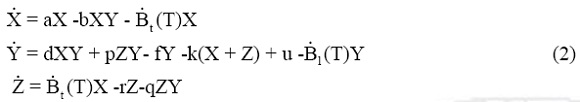
where  t(T) = Bt Σδ (t-Tn) and
t(T) = Bt Σδ (t-Tn) and  1(T) = B1 Σδ(t-Tn) represent the amount of tumor cells and lymphocytes affected by radiation per unit time. Tn are the time instants when radiation doses are applied and δ(t-Tn) denotes Dirac's delta function centered at Tn.
1(T) = B1 Σδ(t-Tn) represent the amount of tumor cells and lymphocytes affected by radiation per unit time. Tn are the time instants when radiation doses are applied and δ(t-Tn) denotes Dirac's delta function centered at Tn.
A dimensionless system can be easily obtained taking the tumor duplication time τc = 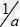 (in absence of external influences) as the characteristic time, so we introduce the dimensionless time τ=
(in absence of external influences) as the characteristic time, so we introduce the dimensionless time τ=  Through the substitutions X = ax/d, Y = ay/b, Z = az/d, we get
Through the substitutions X = ax/d, Y = ay/b, Z = az/d, we get

with ϒ1 (τ) =  1 (τ), ϒt(τ) =
1 (τ), ϒt(τ) =  t (τ), ε= p/d, λ= f/a, κ= kb/ad, σ= ub/a2, ρ= ra/d and η = qa2/db. All parameters can be estimated and interpreted by a similar procedure as in [11].
t (τ), ε= p/d, λ= f/a, κ= kb/ad, σ= ub/a2, ρ= ra/d and η = qa2/db. All parameters can be estimated and interpreted by a similar procedure as in [11].
A linear stability analysis of the system (3) shows that tumor will vanish to L0 = (0; ;0) if
;0) if  and will remain controlled around L1 = ((λ-σ)/(1 -κ); 1; 0) if κ<
and will remain controlled around L1 = ((λ-σ)/(1 -κ); 1; 0) if κ<  or κ>1 [1, 9]. Figure 1 shows stable and unstable regions of Eqs. (3) and highlights region III on which this work will focus.
or κ>1 [1, 9]. Figure 1 shows stable and unstable regions of Eqs. (3) and highlights region III on which this work will focus.
If the system is L0-stable and initial tumour size is small enough, then the radiation treatment is unnecessary, whereas if tumour size is large enough, then the treatment will take it closer to L0. The L1 controlled growth state will be reached only if both parameters fulfill the same condition, in other words, if  and κ are both greater or smaller than unity at the same time. Any other condition makes the first component of L1 < 0, and even when the stable point mathematically exists, it can not be approximated from realistic initial conditions (that should remain positive along the simulation time). For those patients with κ>1 and σ / λ< 1, the main effects of the tumor will be the depression of immune system, they will perform badly according to Karnofsky performance scale [18] and will not fulfill physical requirements to be subject to treatment.
and κ are both greater or smaller than unity at the same time. Any other condition makes the first component of L1 < 0, and even when the stable point mathematically exists, it can not be approximated from realistic initial conditions (that should remain positive along the simulation time). For those patients with κ>1 and σ / λ< 1, the main effects of the tumor will be the depression of immune system, they will perform badly according to Karnofsky performance scale [18] and will not fulfill physical requirements to be subject to treatment.
However for  < κ < 1, tumor will grow and tumor eradication will be achieved only by bringing the system close enough to L0, so that the immune system can get rid of the tumor.
< κ < 1, tumor will grow and tumor eradication will be achieved only by bringing the system close enough to L0, so that the immune system can get rid of the tumor.
The chosen characteristic time and the dimensionless parameters allow us to give a very intuitive interpretation of the critical parameters of Eqs. (3). We can see σ/λ as the efficiency of immune system over tumor growth and κ as the "deficiency" of the immune system due to tumor growth. It is also easy to see that radiation treatments do not change the stability conditions of the system (2), since radiotherapy does not change tumor or lymphocytes growth rate, but can drive the number of both kind of cells to very small values. This means that, for the chosen region in the parameter space, any remaining tumor cells will eventually reproduce and grow after the end of the treatment.
Although Eqs. (3) allow for infinitesimal x values, in real systems when the number of tumor cells becomes small enough, immune system may kill them. In other cases, when a few tumor cells survive, they can cause tumor regrowth. It is known that this behavior is almost independent on tumor size [19]. As an estimation we will assume that if the immune system has a high efficiency it will have higher probabilities of kill the tumor remaining cells and if the immune system has a low efficiency the probability of kill those tumor cells will be low. The simplest linear approximation to deal with this effect is to assume:

as the probability of tumor regression. If no regression occurs, tumor will regrow. We must realize that when the immunodepression term -kX of system (1) is larger than the flux of lymphocytes u, an unattended method to solve the equations will fail to describe a biological system [3]. However, this is a simple way to introduce the immunodepression effect in our equations and can be considered as the first order Taylor approximation for a more general nonlinear function. Furthermore, it provides us a very simple portrait for the parameter space that allows to select the target tumors of radiotherapy treatments. Finally, the chance of lymphocyte population to become zero gives us a natural cutoff for our system. Then, whenever lymphocyte population becomes zero we will assume the tumor escapes lymphocyte control and grows limited only by space and nutrient considerations. At this point, we consider treatment has failed.
2.2 Treatment optimization
A reference protocol was simulated in [1] while coefficients entering equation 3 were varied at random among admissible values [11]. The simulation, then, covers a wide range of tumors and supply general results useful to clinical practice.
One million of "virtual patients" under treatment were simulated. Defining the probability of treatment success (Ps) as the fraction of "virtual patients" with no tumor at the end of treatment, it could be represented as a function of tumor cell survival factor and the Immune System -Tumor efficiency Rate [1], (ISTER), defined as ISTER = σ / λ.
As shown in [1], the long term survival of patients will not improve with higher doses of radiation, on the contrary, it is possible to get the maximum success probability for our reference protocol at intermediate doses. Our model predicts that higher doses do not improve therapy outcomes.
2.3 Simulation
We can mimic different radiation treatments with Eqs. (3) to simulate tumor evolution. To follow radiotherapy treatment in a realistic way, we apply a radiation session every workday (5 consecutive days) and none in weekends (2 days). All treatments [20, 15] begin the tenth day, and apply a variable number of sessions, N, from 20 to 40 for each patient.
We could take up a sort of tumors, i.e. breast or colon, and use an experimental expression to calculate the survival fraction of cells for a 2 Gy dosage. Instead, we preferred to proceed in a more general way, and ignoring the radiation dose, we have taken a random value for the survival fractions of each patient tumor. We have generated several virtual patients under treatment taking different values for the parameter values in Eqs. (3) and use a fourth order Runge-Kutta method [21] to integrate them.
To reproduce tumor evolution resembling that of a clinical case, one needs to calculate the correct values of the cofficients appearing in Eqs. (3). Numerical estimation of these coefficients was already made in [11] (and also in [8] for a slightly different model), based on clinically available data, showing a possible procedure for clinical professionals to estimate their values.
A statistical study of the dependence of treatment success on the dosage and number of radiation sessions was performed. Due to the wide range of possible parameter values in Eqs. (3), their values have been drawn randomly from a log-normal distribution, to avoid negative values, but K keeping the immune system efficiency (σ / λ) always smaller than 1. Survival factors [19, 22] are also taken as random values. As initial conditions we assumed, for simplicity, that the number of tumor cells is higher than the number of lymphocytes and that both initial populations are distributed as normal random numbers.
3 Results and discussion
To describe the success probability for a given treatment let us define the effect potential for tumor cells as

where St is, as before, the survival fraction of cells. This quantity grows monotonously with the radiation dose. If an exponential model like the linear or the LQ model is used to describe the interaction of radiation with living tissues, then the potential becomes the tissue effect. Otherwise, like in the single-hit multi-target inactivation model, it has not a direct interpretation but remains useful to describe the radiation damage.
The treatment success probability, Ps, defined as the fraction of patients with no tumor at the end of treatment, is represented as a function of ISTER, N and χ.

As expected, for each value of N we obtained similar results as obtained in [1]. Furthermore, when a fixed value of the ISTER is taken, the surface represented in figure 2 is obtained. This shows that whenever the value of N increases, the optimized value of PS can be obtained with a lower value of χ per session. This allows to find the exact values of χ that optimize PS, for each value of N, as represented in figure 3.
As a result of the simulations a family of hyperbolas determined by the ISTER value are shown in figure 3. The χ and N values are related by the expression

where R is constant for a fixed ISTER value and Pmax is the maximum success probability the treatment is able to get, given χ and N values. Those R values then could be fitted as a power law of the ISTER,

Our simulations allow to obtain m = -1,1 ± 0,1 and A = 17 ± 1 bringing a method to obtain an approximate value of the maximum success probability that a radiotherapy treatment could reach if the approximate ISTER value is known.
In order to compare R values and how it could characterize the possible radiotherapy treatment outcomes, let us consider a tumor with a very small duplication time compared with the lymphocytes production of the patient but with an almost insignificant immune-depression effect. All tumors with these characteristics can be grouped in region 1 of figure 4. On the other hand, region 2 of the same figure groups tumors with non negligible immune-depression effects but to which immune system could fight satisfactorily and slow down tumor growth.

The parameter R allows to compare without further information the optimal treatments that could be applied. Tumors in zone 1 have a high value of R and even with high radiation doses will not get a good success probability. Taking a standard protocol with 30 sessions as a reference, figure 5 shows that each radiation session must get a value of χ =0,55 and then according to expression 7 a treatment will get less than 14% of success probability.
However an R value between 20 and 30 like in zone 2, guarantee that the final success probability will be high if an optimized treatment is applied. The same standard protocol of 30 sessions must apply a radiation dosage equivalent to χ = 0,6 to get the maximum success probability. Here R = 24 guarantee that if an optimum treatment is applied, a success probability of 75% could be achieved.
Thus, large values of R mean that the success probability of a treatment is low in comparison with the same treatment corresponding to small values of R. The main factor in this analysis is, then, the ISTER. This shows how strongly the immune system influences the results of the radiation treatments and illustrate the importance of considering it as a main factor for radiotherapy.
4 Conclusions
The present work introduces a generalization of [1] to a scenario with a possibly variable number of sessions. Starting from a system of equations and introducing a probabilistic cutoff system, the simulation allows us to find the corresponding effect potential per radiation session providing the maximum value of the success probability. Consider, for instance, that for some time interval the radiotherapy machines are not available when a patient needs an urgent treatment; our work could guide the radiotherapists to design a parallel treatment as efficient as that initially recommended for that patient and adapted to the available time interval.
Finally, an expression that relates the maximum affordable success probability of a treatment with the applied effect potential per session, the number of sessions and the ISTER parameter of a patient was obtained. This shows us that the clinical and experimental study of the interaction between tumor cells and the patient immune system is crucial for RT planning.
References
[1] O Sotolongo-Grau, D Rodriguez Perez, JA Santos Miranda, O Sotolongo- Costa, and JC Antoranz. Immune system-tumour efficiency ratio as a new oncological index for radiotherapy treatment optimization. Math Med Biol, page dqp005, 2009.
[2] VA Kuznetsov, I Makalkin, MA Taylor, and AS Perelson. Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis. Bull Math Biology, 56: 295-321, 1994. [ Links ]
[3] A d'Onofrio. A general framework for modeling tumor-inmune system competition and immunotherapy: Mathematical analysis and biomedical inferences. Physica D, 208:220-235, 2005. [ Links ]
[4] A Matzavinos, M Chaplain, and V Kuznetsov. Mathematical modelling of the spatio-temporal response of cytotoxic t-lymphocytes to a solid tumour. Math Med Biol, 21:1-34, 2004. [ Links ]
[5] A Matzavinos and M Chaplain. Travelling wave analysis of a model of the immune response to cancer. C. R. Biologies, 327:995-1008, 2004. [ Links ]
[6] RK Sachs and LR Hlatky. Simple ode models of tumor growth and anti angiogenic or f radiation treatment. Math. Comp. Modelling, 33:1297-1305, 2001. [ Links ]
[7] D Kirschner and J Panetta. Modelling immunotherapy of the tumor-immune system interaction. J. Math. Biol., 38:235-252, 1998. [ Links ]
[8] L de Pillis, AE Radunskaya, and CL Wiseman. A validated mathematical model of cellmediated immune response to tumor growth. Cancer Research, 65:7950-7958, 2005. [ Links ]
[9] O Sotolongo-Costa and et al. Behavior of tumors under nonstationary therapy. Physica D, 178:242-253, 2003. [ Links ]
[10] Galach M. Dynamics of the tumor-immune system competition - the effect of time delay. Int J Appl Math Comput Sci, 13:395-406, 2003. [ Links ]
[11] D Rodriguez-Perez, O Sotolongo-Grau, R Espinosa Riquelme, O Sotolongo-Costa, JA Santos Miranda, and JC Antoranz. Assesment of cancer immunotherapy outcome in terms of the immune response time features. Math Med Biol, 24:287-300, 2007. [ Links ]
[12] D Dingli, MD Cascino, K Josic, SJ Russell, and Z Bajzer. Mathematical modeling of cancer radiovirotherapy. Mathematical Biosciences, 199:55-78, 2006. [ Links ]
[13] LG dePillis, W Gu, and AE Radunskaya. Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations. Journal of Theoretical Biology, 238:841-862, 2006. [ Links ]
[14] H Enderling, MAJ Chaplain, ARA Anderson, and J Vaidya. A mathematical model of breast cancer development, local treatment and recurrence. Journal of Theoretical Biology, 246:245- I 259, 2007. [ Links ]
[15] VS Khoo. Radiotherapeutic techniques for prostate cancer, dose escalation and brachytherapy. Clinical Oncology, 17:560-571, 2005. [ Links ]
[16] TL Whiteside. Apoptosis of immune cells in the tumor microenvironment and peripheral circulation of patients with cancer: implications for immunotherapy. Vaccine, 20:A46-A51, 2002. [ Links ]
[17] TL Whiteside. Immune suppression in cancer: Effects on immune cells, mechanisms and future therapeutic intervention. Seminars in Cancer Biology, 16:3-15, 2006. [ Links ]
[18] S Sundstrom, R Bremnes, U Aasebo, S Aamdal, R Htlevoll, P Brunsvig, DC Johannessen, O Klepp, PM Fayers, and Kaasa S. Hypofractioned palliative radiotherapy (17 Gy per two fractions) in advanced non-small-cell lung carcinoma is comparable to standard fractionation for symptom control and survival: A national phase III trial. Journal of Clinical Oncology, 22:801-810, 2004. [ Links ]
[19] GG Steel. Basic Clinical Radiobiology for Radiation Oncologists. Edward Arnold Publishers, London, 1993. [ Links ]
[20] D Rades and S Lang. Prognostic value of haemoglobin levels during concurrent radiochemotherapy in the treatment of oesophageal cancer. Clinical Oncology, 18:139-144, 2006. [ Links ]
[21] WH Press, SA Teukolsky, WT Vetterling, and BP Flannery. Numerical Recipes in C, The Art of Scientific Computing. Cambrige, Cambrige University Press, 1992. [ Links ]
[22] H Enderling, RA Alexander, and AJ Mark. Mathematical modelling of radiotherapy strategies for early breast cancer. Journal of Theoretical Biology, 241:158-171, 2006. [ Links ]














