Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nova scientia
versión On-line ISSN 2007-0705
Nova scientia vol.4 no.8 León oct. 2012
Ciencias naturales e ingenierías
Transmisión para una superred con modulación lineal de los anchos de las barreras
Transmission for a superlattice with linear modulation of the barriers width
A. H. Barajas-Aguilar1, A. Enciso-Muñoz1 and D. A. Contreras-Solorio1
1 Unidad Académica de Física. Universidad Autónoma de Zacatecas, México.
D. A. Contreras-Solorio. Apartado Postal 157, 98000 Zacatecas, Zac., México. E-mail: dacs10@yahoo.com.mx
Recepción: 10-10-2011
Aceptación: 06-01-2012
Resumen
Usando el método de la matriz de transferencia y la ecuación de Ben Daniel y Duke para | propagación de electrones con masa variable, calculamos la transmitancia para una superred lineal finita simétrica que tiene variación lineal del ancho de las barreras de potencial. El ancho de las barreras decrece del centro hacia los extremos de la superred. La dependencia en la energía de la transmitancia presenta intervalos de bandas de rechazo y de bandas bastante planas de transmisión. Realizamos los cálculos de transmisión para varias alturas de barreras y varios anchos de pozos. Comparamos con la transmisión de una superred regular en la cual todas las barreras tienen el mismo ancho. También comparamos con la de una superred lineal invertida en que el ancho de las barreras crece del centro hacia afuera, así como con la de una estructura donde la variación de los anchos de barreras sigue un perfil gaussiano.
Palabras clave: Transmitancia, superred, electrones, pasabanda, filtro.
Abstract
Using the transfer matrix method and the Ben Daniel-Duke equation for variable mass electrons propagation, we calculate the transmittance for a symmetric finite superlattice which has a linear dependence for the width of the potential barriers. The width of the barriers decreases from the center toward to the ends of the superlattice. The energy dependence of the transmittance presents intervals of stopbands and quite flat passbands. We calculate the transmission for several heights of barriers and widths of wells and compare with the transmission of a regular superlattice where all the barriers have the same width. We also compare with an inverted linear superlattice where the barriers width increases from the center to the ends, as well with the transmission produced by a superlattice with a Gaussian variation of the barriers width.
Keywords: Transmittance, superlattice, electrons, passband, filter.
Introduction
The subject of propagation of any kind of waves in layered structures is very important. One of their important applications is as reflector structures and as filters. The search for energy, electronic, optical and acoustic filters is an interesting and active field. There have been proposals of energy passband filters using quantum superlattices with a Gaussian potential profile (Tung, 1996 and Gómez, 1999). These layered structures allow the incident electrons to be nearly totally transmitted when the impinging electron energy is in the passband energy region. Also, a complete reflection occurs when the impinging energy is in the stopband energy region. The idea behind using these types of structures is that a Gaussian profile provides a slowly varying potential for the layers, which can improve the transmission of electrons through the multilayer system. Following the idea of the superlattices with a Gaussian potential profile, layered omnidirectional optical mirrors have been proposed where the refractive index varies according to the envelope of a Gaussian function, using only normal materials (Arriaga, 2006) and using also metamaterials (Saldaña, 2008). These systems were proposed only as omnidirectional mirrors but their properties as optical filters were not investigated. However, there is a proposal of a multilayer optical filter where the refractive index of the layers is modulated by a Gaussian function (Madrigal, 2009). Likewise, there is a proposal of a layered acoustic filter where the characteristic acoustic impedance of the layers is modulated by a Gaussian distribution (Madrigal, 2008). In this work we propose a symmetric structure where the width of the potential barriers follows a linear profile. The widest barrier is at the center of the superlattice and the narrowest ones are at the ends. For the calculations we use the transfer matrix method and the Ben Daniel-Duke equation for variable mass electrons (Ben Daniel, 1966). The spectrum of transmittance of the structure presents stopbands and nearly flat transmission bands of energy. We compare this transmittance with that produced by a superlattice where the barriers width have a Gaussian modulation, as well as for a structure where all the barriers have the same width, and also for a superlattice where the barriers width increases from the center to the ends. In the next section we introduce the theoretical background, then we present some of our results and discussion of the behavior of the transmittance and finally we give some conclusions.
Method
The propagation of the electrons in the structure is described by the Ben Daniel-Duke equation, appropriate for electrons with variable effective mass m*.
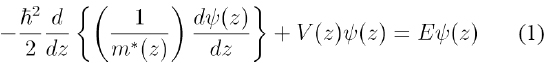
The boundary conditions are the continuity of Ψ(z) and 1/m* (dΨ/dz). In order to solve the previous equation we use the theory for transfer matrix of (Pérez, 2004). We consider a system of n coupled differential equations of second order with variable coefficients,
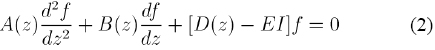
With

And A, B y D are n x n matrices, I is the identity matrix, fi(z) are the n unknown functions of the system. We also use the notation:

The system can be changed to another system of 2n equations of first order F'=PF where
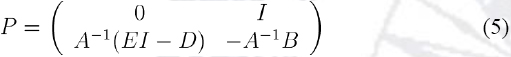

F is a column vector of 2n components, and P is a 2n x 2n matrix. The system F' = PF has 2n independent solutions Fj, with j = 1,2,3,... 2n. Every solution F of the system can be expressed as a linear combination

The matrix M of complete transfer is defined as:

or also
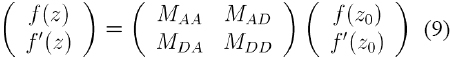
Where the Mαβ are n x n blocks of the transfer matrixM (z, z0). This matrix transfers the solution at z0 to another point z. M is called a complete transfer matrix because it transfers ƒ and also ƒ', in order to distinguish it from the matrix that transfers only ƒ.
We consider the electrons as plane waves. The transmittance T is given by the ratio of the transmitted probability current density to that of the incident one, and is given in terms of the transfer matrix by
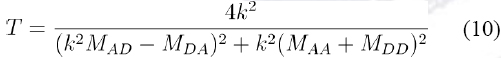
Where k is the wave vector for zero potential.
Results
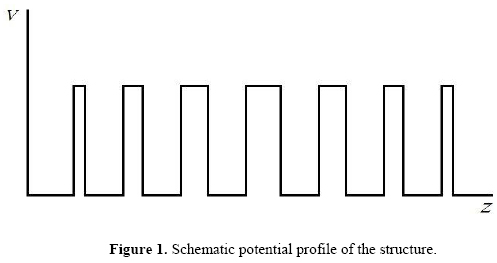
We consider a superlattice made of N layers, the barriers are the layers with odd numbering, while the wells have even numbering. The width hi of the barriers follows a symmetric linear profile while the wells width is constant. hmax is the width of the widest barrier considered at the center of the structure and hmin the width of the narrowest ones at the ends of the structure. The superlattice is shown schematically in Fig. 1.
We consider that the multilayer structure is constructed changing the mole fraction of the semiconductor alloy AlxGa1-xAs. The wells are made of pure GaAs whereas the barriers are made of AlxGa1-xAs. In order to calculate the electron effective mass m for the alloy, we use the virtual crystal approximation (Singh, 1993), with
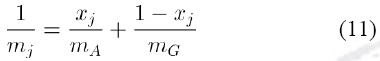
mA and mG being the electron effective masses for pure AlAs and GaAs. We consider a maximum concentration x of 0.45, for which the alloy AlxGa1-xAs has still a direct gap of 1.98 eV. For GaAs we take a gap of 1.42 eV and a band offset of 0.6 for the conduction band at the interface GaAs / AlxGa1-xAs. With these values, the maximum height for the barriers V0 which can be considered is 0.33 eV and the concentration is given by x = V/ 0.733, where V is the height of the barriers for the superlattice. We present results for a superlattice of 25 layers, for which 13 are barriers and 12 are wells. The width of barriers and wells is given in monolayers (ML), one ML has a thickness of 2.825 Å. The width hmin for the barriers is 1 ML and hmax, the widest barrier at the center of the superlattice, is 7 ML. We show in Fig. 2 the transmission for a structure with a wells width of 22 ML and height of the potentials V=0.15 eV.
In Fig. 3 the transmission is for a superlattice where the height of the barriers is 0.25 eV and the wells also have a width of 22 ML. For fixed width of barriers and wells, when the height of the potential barriers increases, the electrons are more confined, the lifetime Δt of the eigenstates increases, and by the uncertainty principle ΔE Δt≥ħ/2, the band width ΔE of the resonance curves decreases. Since the passband is the envelope of the resonance curves this reduction causes the passband to be narrower for an increase of the potential. These two cases of Figs. 2 and 3 present a quite flat passband. We present in Fig. 4 in black the transmission for a superlattice with barriers height of 0.20 eV and wells width of 20 ML. For comparison we also present in red, the transmission of a regular superlattice where the 13 barriers have the same width of 7 ML.We stress the flatness of the passband for the superlattice with a linear variation of the barriers width in opposition to the transmission for the regular structure. The passband for the regular superlattice presents oscillations which are the peaks or curves of resonance for the eigen energies due to the 12 wells of the superlattice. A regular structure does not have flat passbands. The decrease of the barrier width from the center toward the sides of the structure causes a drop of the lifetime Δt for the eigenstates, due to the fact that the electrons tunnel more easily. For the above mentioned uncertainty principle, the resonance bandwidth ΔE increases and the passband, which is the envelope of the resonance curves, becomes flatter.
Also for comparison, we present in Fig. 5 the transmittance for the regular structure of Fig. 4 and the transmittance for an inverted superlattice with an opposite linear variation of the barriers width, where the narrowest barrier is at the center of the structure while the widest ones are at the ends. For this last structure the electrons are more confined that in the regular structure and the resonance peaks are narrower. Finally, we compare the transmittance for our superlattice with linear variation of the barriers width with that produced by a superlattice with a Gaussian variation. This type of variation has been used before for producing also flat passbands for the transmission of a superlattice (Tung, 1996 and Gómez, 1999). We generate the barriers widths for a Gaussian structure with 13 barriers using the function hi=hmax exp(-i2/2σ2), where σ is the standard deviation and i=0, 2, 6. hmax is the widest barrier at the center of the Gaussian superlattice. For a Gaussian variation we need to consider a larger value of hmax than for a linear variation. We calculate a and the minimum hmax which produce the best flat passband for a superlattice with hmin=1 ML and wells width of 20 ML. Our results give σ=2.66 and hmax=13 ML. We carried out the calculations for hmax in angstroms and round off the widths hi in ML. We show in Fig. 6 our results.
We see that the flatness for both types of superlattices is comparable, but the passband for the Gaussian superlattice is narrower. Besides that, is more difficult to work with a Gaussian structure because one has to calculate σ, hmax and the wells width in order to reproduce hmin and a flat passband, while for the linear structure one simply provides hmax and hmin and make a variation of the wells width in order to search for a flat passband.
Discussion
Using the one-band effective mass framework together with the Ben Daniel-Duke equation for variable effective mass and a method of transfer matrix which transfer a function and its derivative, we have made studies of the electrons transmittance for a finite superlattice where the width of the potential barriers follows a linear distribution, with the widest barrier at the center of the superlattice and the narrowest at the ends. The transmittance presents a quite flat passband which can not be obtained with a regular structure where all the barriers have the same width. Moreover, the structure with linear variation of barriers width produces a flat passband wider than that produced by a structure with a Gaussian variation. Besides that, a superlattice with a linear variation of barriers width is easier to construct than a structure with Gaussian variation. A superlattice with linear variation of barriers width can have applications as an energy filter for electrons, allowing electrons of selected intervals energies to pass through.
Acknowledgments
This work has been supported partially by Universidad Autónoma de Zacatecas, PROMEP and Consejo Zacatecano de Ciencia y Tecnología (COZCyT).
References
Arriaga, J. and X. Saldaña. 2006. Band structure and reflectivity of omnidirectional Si-based mirrors with a Gaussian profile refractive index. J. Appl. Phys. 100(4): 044911. [ Links ]
Ben Daniel, D. J. and C. B. Duke. 1996. Space-charge effects on electron tunneling. Phys. Rev. 152:683-692. [ Links ]
Gómez, I., F. Domínguez-Adame, E. Diez, and V. Bellani. 1999. Electron transport across a Gaussian superlattice. J. Appl. Phys. 85(7): 3916-3918. [ Links ]
Madrigal Melchor, J., Agustín Enciso Muñoz, X. I. Saldaña y D. A. Contreras Solorio. 2009. Filtro óptico multicapas con variación gaussiana del índice refractivo. LII Congreso Nacional de Física, Acapulco, Guerrero, México. [ Links ]
Madrigal-Melchor, J., R. A. Reyes-Villagrana, X. Saldaña, S. Jelev-Vlaev, and D. A. Contreras-Solorio. 2008. Acoustic layered filter with a Gaussian distribution of impedances. SLAFES, Book of Abstracts. Iguazú, Argentina. [ Links ]
Pérez-Álvarez, Rolando, F. García-Moliner. 2004. Transfer matrix, Green functions and related techniques. Universitat Jaume I, Spain. [ Links ]
Saldaña Saldaña, X. I, D. A. Contreras Solorio y A. Enciso Muñoz. 2008. Reflectancia de una estructura multicapas con intercalado de materiales izquierdos. 20 Encuentro Nacional de Investigación Científica y Tecnológica del Golfo de México, Cd. Victoria, Tam., México. [ Links ]
Singh, Jasprit. 1993. Physics of semiconductors and their heterostructures. McGraw-Hill. [ Links ]
Tung, H. H. and C. P. Lee. 1996. An energy band-pass filter using superlattice structures. IEEE J. I Quantum Electron. 32: 507-512. [ Links ]














