1. Introduction
Titanium sulphide is a semi-metallic in its ground state. Yan-Bin et al. (Yan-Bin et al, 2007) reported the metallic behaviour in the self-intercalated TiS2 where the coulomb interaction with metal Ti-atom decreases the overlapping of orbitals. The Ti(3d)-S(3p) hybridization is responsible for the covalent bonding in TiS2. Transition metal chalcogenides show interesting behaviour due to their layered and two dimensional symmetric structures. The metallic species can be easily intercalated into the pure material which is possible due to weak interlayer van der waals attraction (vdW). Strong hybridization occurs among M(3d), Ti(3d) and S(3p) with intercalation with transition metals (M). These chalcogenides have been useful in forming a family of intercalcated compounds (Bardhan, Kirczenow & Irwin, 1985; Tonti, Pettenkofer & Jaegermann, 2004; Whittingham, 1987). TiS2 has been utilised for oxygen catalyst for fuel cells (Baresel, Sarholz, Scharner, Schmitz & Bunsen Ges, 1974) whereas Li-TiS2 has been explored as a future material for high energy batteries (Abraham & Alamgir, 1991). These observations have been supported by angle resolved inverse photoemission spectroscopy (ARIPES), angle resolved resonant photoemission spectroscopy (ARPES), X-ray photoemission spectroscopy (XPS) and high field magnetization measurements (Matsushita, Suga, Kimuta, Negishi, & Inoue, 1999; Ueda et al., 1986).
The bonding behaviour in intercalcated TiS2 has been studied theoretically (Cui et al., 2006; Kim, Li, Tanaka, Koyama & Adachi, 2000; Suzuki, Yamasaki & Motizuki, 1988; Yamasaki, Suzuki & Motizuki, 1987). It has been pointed out that the transport properties of MTiS2 are unusual and are dependent on those of the guest atom (Inoue, Moneta, Neigh & Sasaki, 1986; Inoue, Sadahiro & Negishi, 1991; Negishi, Yamada, Yuri & Inoue, 1997; Tazuke et al., 1988; Takase et al., 2000).
Recently, Sharma, Shukla, Dwivedi and Sharma (2015), have studied the electronic and transport properties of MTiS2 (M = Cr, Mn and Fe). However, they have not addressed the mechanical properties of these compounds. In the present work the electronic, structural and mechanical properties of unpolarised TiS2, TiS2Cr and spin-polarised TiS2Cr have been investigated in the framework of density functional theory (DFT).
2. Methodology
All the calculations have been performed by Abinit software based on norm conserving pseudopotential method within density functional theory (DFT) (Gonze et al., 2002; 2005; 2009; Hohenberg & Kohn, 1964; Kohn & Sham, 1965; http://www.abinit.org). The generalized gradient approximation (GGA) using Perdew Burke Ernzerhof (PBE) formulation (Perdew, Burke & Ernzerhof, 1996) has be utilized to include exchange-correlation effects. The wave functions from real to reciprocal lattice have been converted using fast fourier transform algorithm (Goedecker, 1997). The wave functions have been determined self-consistently using conjugate gradient algorithm approach (Gonze, 1996; Payne, Teter, Allan, Arias, & Joannopoulos 1992). The Monkhorst-Pack scheme has been used for the integration over the Brillouin zone (BZ) (Monkhorst & Pack, 1976). The convergence with respect to plane wave cut-off energy and k-points has been checked. Accordingly, a plane wave cut-off energy of 80 Ry and k-mesh of 8x8x8 have been used. The lattice constants have been relaxed to get the minimum energy. In order to get convergence, system is relaxed until the differences between energies or forces in two consecutive steps are less than 27x10-6 meV and 2.6 meV/Å, respectively.
Abinit software has been utilized to calculate the elastic constants using the linear-response method. The linear response method is based on second order derivative of the total energy with respect to the strain. For the visualization of the crystal structure and 2D charge density, Xcrysden (Kokalj, 1999) software has been used.
3. Results and Discussion
TiS2 has a CdI2 type hexagonal crystal structure with space group P
The lattice constants ‘a’ and ‘c’ of unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds have been computed and given in Table 1. The equilibrium lattice constant has been achieved by changing lattice constant and computing the energy equivalent to each lattice constant. The lattice constant corresponding to lowest energy is considered as an equilibrium lattice constant. The lattice constant values obtained in present study for unpolarized TiS2 and TiS2Cr are in agreement with available theoretical values (Fang, De Groot & Hass, 1997; Yamasaki et a., 1987). However, the slight variation in the lattice constant values between present results and pervious values are attributed due to the differences in the calculation schemes.
Table 1. The equilibrium lattice constants, calculated single crystal elastic constants for unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds. The other available theoretical values for lattice constants are also given for comparison (Yamasaki, Suzuki &Motizuki, 1987; Fang, de Groot & Hass, 1997).
| System | Magnetic-effect | a (Å) |
c (Å) |
C11 (GPa) |
C12 (GPa) |
C13 (GPa) |
C33 (GPa) |
C44 (GPa) |
|---|---|---|---|---|---|---|---|---|
| TiS2 | unpolarized |
|
|
98 | 35 | 51 | 79 | 48 |
| TiS2Cr | unpolarized |
|
|
150 | 58 | 94 | 185 | 76 |
| spin-polarized |
|
|
203 | 54 | 107 | 259 | 134 |
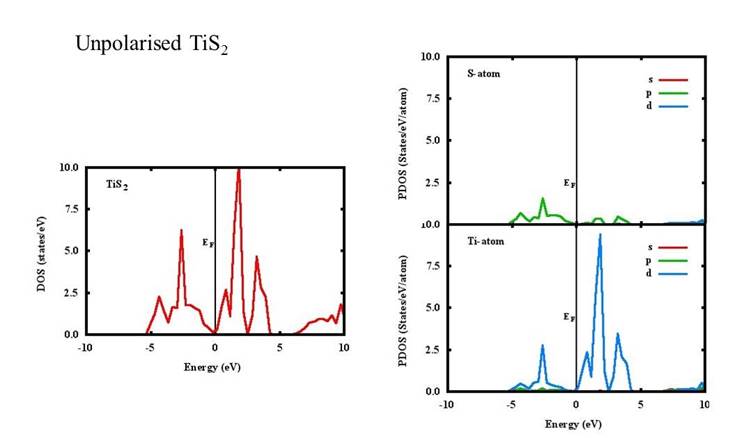
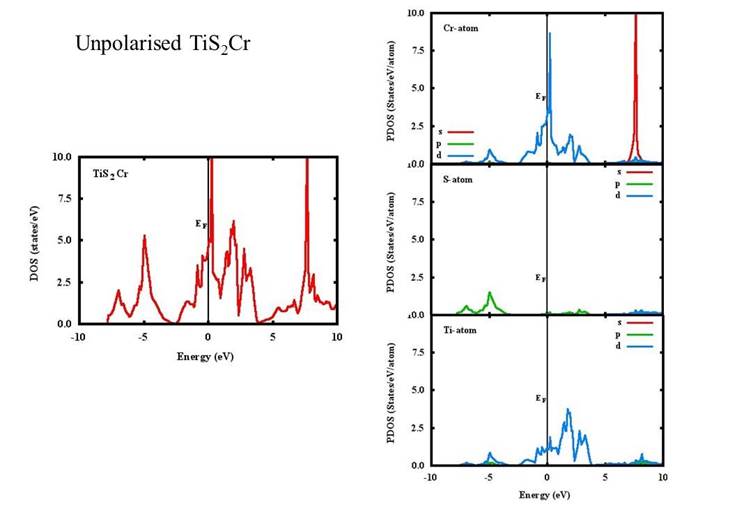
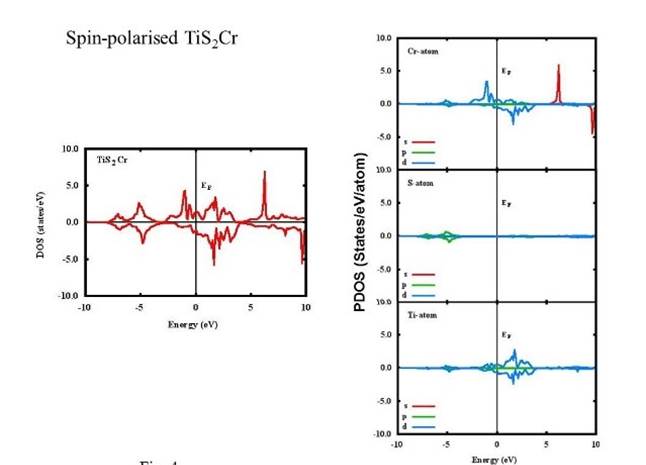
Density of states (DOS) and projected density of states (PDOS) of the unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds are given in Figs. 2-4. The DOS for TiS2 has a minimum at Fermi level (EF) compared to a high peak in both unpolarized and spin polarised TiS2Cr.
The DOS for the TiS2 (Fig. 2) can be divided in three energy regions from -5 to 0, 0 to 5 and 5 to 10 eV. In the low energy region, there are two major peaks around -4.5 and -2.7 eV because of p and d orbital contribution of S and Ti atoms, respectively. In the 0-5 eV region, three peaks are found around 0.7, 1.8 and 3.3 eV mainly because of S(p) and Ti(d) orbital contributions whereas in high energy region (5-10 eV), a continuous energy band are seen. Similar behaviour of the DOS and peaks at similar positions are found in other published reports (Fang, Groot & Hass, 1997; Reshak, Kityk & Auluck, 2008; Sharma et al., 1999; Sharma et al., 2015). For unpolarised TiS2Cr, the DOS can be divided in three energy regions namely, -7.5 to -2.5, -2.5 to 4 and 4 to 10 eV (Fig. 3). In the low energy region, two peaks are found around -7.0 and -5.0 eV. The peak at -5 eV is because of Cr(d), Ti(d) and S(p) orbital contributions. A continuous band found close to Fermi level having peaks at 0.2, 2.0 and 2.8 eV mainly because of Cr(d) and Ti(d) orbital contributions. In high energy region, again a continuous band with a high peak at 7.6 eV is found mainly because of Cr(s) orbital contribution.
Additionally, DOS for the spin-polarised TiS2Cr in spin up and spin down has been shown in Fig. 4. The DOS for spin up can be divided in three energy regions namely, -8.0 to -2.8, -2.8 to 4 and 4 to 10 eV. For low energy region, two peaks are found at -7.1 and 5.2 eV mainly due to Cr(d), Ti(d) and S(p) orbital contribution, whereas continuous band having peaks at -1.0, 1.8 and 2.5 eV are found close to Fermi level mainly because of Cr(d) and Ti(d) orbital contributions. In high energy region, a continuous band with one major peak at 6.2 eV is found mainly because of Cr(s) orbital contribution. Slightly shifted peaks are found in down spin. Further, the nature and location of peaks found in the present study are in good agreement with the reported peaks by Sharma et al. (2015). Two peaks (at 6.2 eV in up spin and 9.6 eV in down spin) which are originated due to s-orbital contribution of Cr-atom are not found in Sharma et al. (Sharma et al., 2015). Also, the PDOS shows strong Ti(d)-S(p) bonding for TiS2 whereas strong Cr(d)-S(p), Cr(d)-Ti(d) and Ti(d)-S(s) bonding in unpolarised and spin-polarised TiS2Cr (Figs. 2-4).
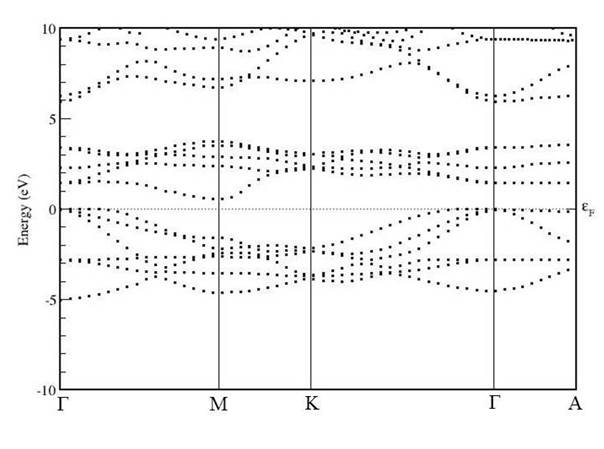
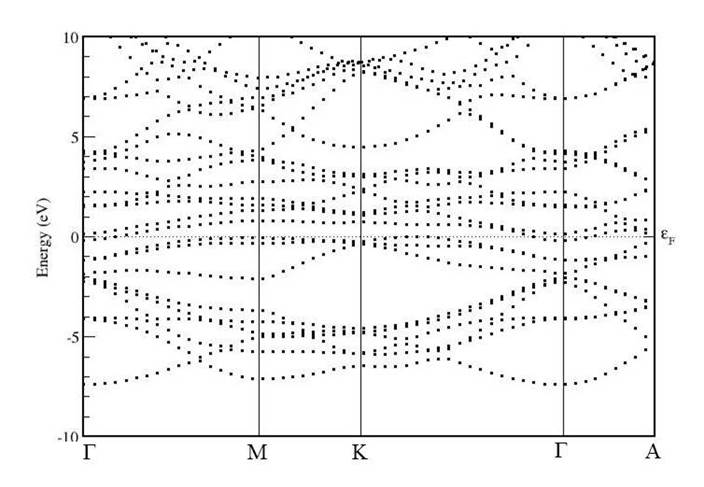
Further, the electronic band structures of unpolarised TiS2, unpolarised TiS2Cr and spin-polarised TiS2Cr have been shown in Figs. 5-7. These band structures are plotted in the high symmetry Γ-M-K- Γ-A directions in the irreducible brillouin zone (IBZ). It is to be noted that Fermi level (EF) is set to 0 eV.
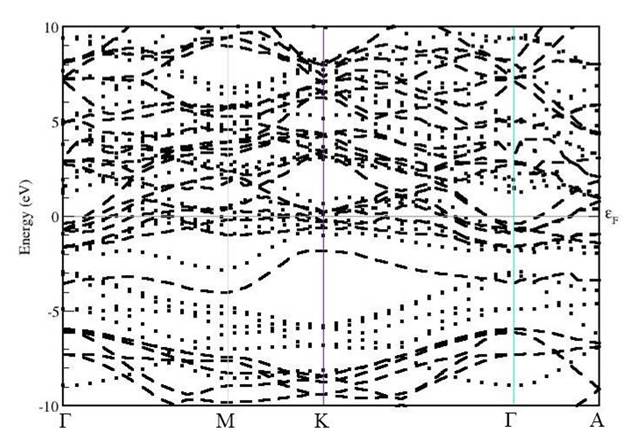
Fig. 7. Energy band structure for spin-polarized TiS2Cr along Γ-M-K-Γ-A directions. Spin up and spin down band structures are shown with dotted and break lines, respectively.
For TiS2, the band structure can be divided into two energy regions namely, -5 to 0 eV and 0 to 5 eV. These two regions are also called as bonding (-5 - 0 eV) and antibonding regions (0 - 5 eV). In the lower energy region, the energy states are because of p and d orbital contribution of S and Ti atoms, respectively. In conduction band region (0 to 5eV) the energy states are mainly due to S(p) and Ti(d) orbital contributions. The valence band maximum (VBM) and the conduction band minimum (CBM) are found at Γ and M symmetry points, respectively. Similar behaviour of band structure for TiS2 has been found in other published reported (Fang, et al., 1997; Reshak et al., 2008; Sharma, Naut, 1999; Sharma et al., 2015).
For unpolarised TiS2Cr, the band structure is divided into three energy regions. These are -7.5 to 0 eV, 0 to 5eV and 5 to 10 eV. In lower region, energy sates are of similar nature of parent TiS2. However, the energy states are shifted towards lower energy side. These states are because of Cr(d), Ti(d) and S(p) orbital contribution. In the vicinity of EF, near VBM and CBM additional states compared to TiS2 are found mainly because of d-orbital contribution of Cr atom. In high energy region, apart from original states seen in TiS2 few other states are also found due to Cr atom.
Further, for the spin-polarised TiS2Cr, the spin up and spin down band structures are shown in Fig. 7. The band structure can be divided in three energy regions namely, -10 to -5 eV, -5 to 5 eV and 5 to 10 eV, respectively. In the lower region, slightly shifted and similar to TiS2 energy states are found mainly because of Ti(d) and S(p) orbital contribution. Near EF, a dense states due to mixing of different atomic states mainly due to d-orbital contribution of Cr and Ti atoms. In high energy region, a part from original states in TiS2 few new states because of Cr atom are found. Finally, due to intercalation of Cr atom, the band structure modifies significantly and there is enhancement in the number of energy states in valence and conduction regions.
The corresponding 2D charge density distributions of the unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds are shown in Figs. 8-10. TiS2 displays strong and weak electronic interactions for Ti-S and S-S bonds respectively. TiS2Cr shows strong electronic interactions for Cr-S compared to Ti-S and S-S bonds. The spin-polarization density or magnetization charge density (spin up minus spin down density) for spin-polarized TiS2Cr compound (Fig. 10) shows that net magnetization for S atom is nearly zero whereas finite magnetization for Cr and Ti atoms. The extent of magnetization in Cr atoms is higher compared to Ti atoms. This is also supported by the calculated magnetic moment values for spin-polarized TiS2Cr. The magnetic moments for Ti (mTi), Cr (mCr) and (mS) are -0.039 µB, 2.393 µB and -0.007 µB, respectively. The atomic magnetic moment for Ti (mTi) is anti-parallel to the Cr atom, indicating that spin-polarized TiS2Cr compound is ferromagnetic.
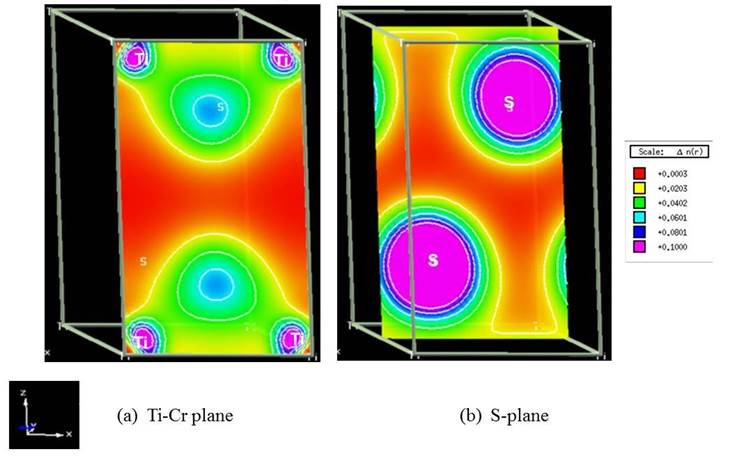
Fig. 8. 2D charge density distribution for the unpolarized TiS2 compound in X-Z plane. Plane directions and charge density scales, units are also shown.
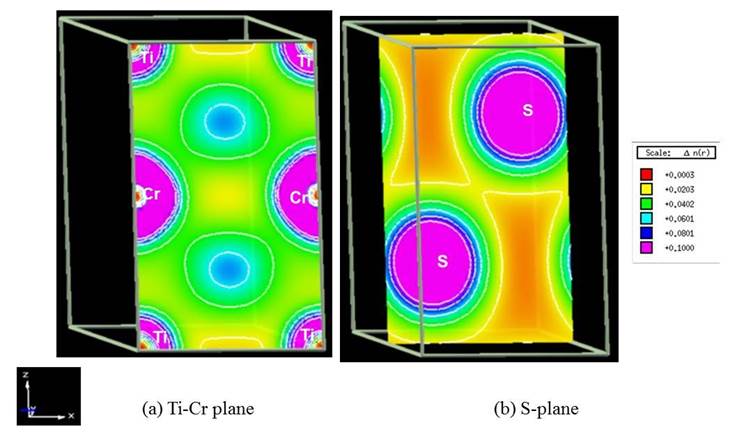
Fig 9. . 2D charge density distribution for the unpolarized TiS2Cr compound in X-Z plane. Plane directions and charge density scales, units are also shown.

Fig. 10. 2D spin polarization density (spin up minus spin down charge density) for the spin-polarized TiS2Cr compound in X-Z plane. Plane directions and charge density scales, units are also shown.
The single crystal elastic properties of hexagonal structure are defined by five independent elastic constants namely, C11, C12, C33, C13 and C44 and are given in Table 1. The nature of atomic bonding for hexagonal structures can be predicted based on Cauchy pressures (Pettifor & Aoki, 1991). These are well-defined as
The negative Cauchy pressure shows directional bonding whereas positive value displays predominant metallic bonding. The computed values of Cauchy pressures of unpolarized TiS2 and TiS2Cr compounds are positive (Table 2) compared to negative values for spin-polarized TiS2Cr. This clearly points towards the presence of major metallic bonds in unpolarized TiS2 and TiS2Cr whereas directional bonding in spin-polarized TiS2Cr.
Table 2. Calculated Cauchy pressures (C1, C2), Born stability criteria (S1, S2, S3, S4 and S5) and anisotropic values (A1, A2 and A3) for unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds.
| System | Magnetic-effect | C1 | C2 | S1 | S2 | S3 | S4 | S5 | A1 | A2 | A3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | ||||||||||
| TiS2 | unpolarized | 3 | 3.5 | 35 | 79 | 48 | 31.5 | 5305 | 1.52 | 0.81 | 0.69 |
| TiS2Cr | unpolarized | 18 | 12 | 58 | 185 | 76 | 46 | 20808 | 1.65 | 1.23 | 0.62 |
| TiS2Cr | Spin-polarised | -27 | -20.5 | 54 | 259 | 134 | 74.5 | 60731 | 1.80 | 1.28 | 0.51 |
The values of elastic constants can also be utilized to predict the mechanical stability of these compounds. The Born stability criteria for hexagonal crystals are given in Equations (2) and (3) respectively (Born, 1940; Fedorov, 1968).
and
The values for Born stability criteria suggest that these compounds (unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr) are mechanically stable (Table 2). The anisotropy aspects (A) for hexagonal structure are defined below.
The values of anisotropic factors should be unity for an isotropic crystal whereas away from unity point towards the presence of anisotropy. The anisotropic values (A1, A2, A3) obtained in present study for unpolarized TiS2, TiS2Cr are (1.52, 0.81, 0.69), (1.65, 1.23, 0.62) respectively whereas for spin-polarized TiS2Cr is (1.80, 1.28, 0.51). These values of anisotropic factors are away from unity indicating the presence of anisotropy in these materials.
Further, in the present study, these anisotropy values are also related to atomic bonding between different layered atoms. For TiS2 system, z axis atomic positions are Ti (z= 0.0 Å), S1 (z = 1.4648 Å) and S2 (z = 4.3943 Å), respectively. The three Ti-S1 bond lengths are 2.4982 Å and forth one is 4.3043 Å. The S1-S2 bond length is 3.5606 Å. For unpolarised TiS2Cr, z axis atomic positions are Ti (z = 0.0 Å), S1 (z = 1.4751 Å), Cr (z = 2.9502 Å) and S2 (z = 4.4253 Å), respectively. The three Ti-S1, three Cr-S1 and the three Cr-S2 bond lengths are equal (2.5158 Å). The forth bond for Ti-S1, Cr-S1 and Cr-S2 are also same (4.3347 Å).
Finally, for spin-polarised TiS2Cr, z axis atomic positions are Ti (z = 0.0 Å), S1 (z = 1.4753 Å), Cr (z = 2.9506 Å) and S2 (z = 4.4258 Å), respectively. The neighbouring bonds for Ti-S1, Cr-S1 and Cr-S2 are of equal magnitude (2.5160 Å). One bond for Ti-S1, Cr-S1 and Cr-S2 are of magnitude (4.3351 Å). Therefore, the magnitude of atomic bonding between Ti-S1, Cr-S1 and Cr-S2 is same after the intercalation of Cr atom in the TiS2 system. Further, the elastic anisotropic values such as A1 and A2 increase after the intercalation of Cr atom in the TiS2 system (Table 2). This indicates that the atomic bonds along z-direction and shear plane perpendicular to z-direction are stiffer after intercalation of Cr atom in the TiS2 system.
For polycrystalline hexagonal materials, Voigt (1928) and Reuss (1929) approximations can be utilized to estimate the upper and lower limit of elastic modulus. These are
Where B is bulk modulus while GV and GR are shear modulus values obtained by Voigt and Reuss approximations respectively.
The average value of these two estimates mentioned above is given by Hill (1952) approximation for hexagonal materials. The Voigt-Reuss-Hill (VRH) average values are given by
Where B (=BH), G (=GH), E and ν are bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio, respectively.
The bulk modulus, shear modulus and Young’s modulus (Table 3) exhibit maximum value for spin-polarized TiS2Cr followed by unpolarized TiS2Cr and TiS2. The values of shear and bulk modulus can also be utilized for The brittle and ductile behaviour of materials can also be predicted by taking ratios of G and B (Pugh, 1954). If the ratio (G/B) greater than 0.57, material is brittle otherwise related with ductile behaviour. Based on the G/B ratio, the spin-polarized TiS2Cr is brittle whereas unpolarized TiS2Cr and TiS2 are ductile.
Table 3. Calculated polycrystalline mechanical properties such as Bulk modulus (B), Shear Modulus (G), Young’s modulus (E), G/B ratio and Poisson’s ratio (υ) for unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds.
| System | Magnetic-effect | B (GPa) |
GV (GPa) |
GR (GPa) |
G (GPa) |
E (GPa) |
G/B | υ |
|---|---|---|---|---|---|---|---|---|
| TiS2 | unpolarized | 61 | 35 | 29 | 32 | 81 | 0.525 | 0.28 |
| TiS2Cr | unpolarized | 106 | 55 | 53 | 54 | 139 | 0.509 | 0.28 |
| spin-polarized | 130 | 91 | 86 | 89 | 217 | 0.685 | 0.22 |
Debye temperature (θD) is one of the most significant parameter and it decides the thermal characteristics of the materials. The Debye temperature (θD) can be obtained from the mean sound velocity and can be calculated from the certain relations (Anderson, 1963; Sun, Ahuja & Schneider, 2004).
where vL, vT and vm are the longitudinal, transverse and mean sound velocities obtained using the shear modulus (G), bulk modulus (B) and the density (ρ).
The Debye temperature (θD) can be given as
where h is the Planck’s constant, k is the Boltzmann’s constant, N A is the Avogadro’s number, ρ is the density, M is the molecular weight, n is the number of atoms in the unit cell, and v m is the mean sound velocity.
The calculated values of longitudinal sound velocity (vL), transverse sound velocity (vT), mean sound velocity (vm) and Debye temperature (θD) have been given in Table 4. The higher θD suggests the higher thermal conductivity associated with the material. Present study suggests that the value of θD is maximum for the spin-polarised TiS2Cr followed by unpolarized TiS2Cr and TiS2.
Table 4. Calculated unit cell volume, density (ρ), longitudinal sound velocity (vL), transverse sound velocity (vT), mean sound velocity (vm) and Debye temperature (θD) for unpolarised TiS2, TiS2Cr and spin-polarised TiS2Cr compounds.
| Alloy | Magnetic-effect | Volume (Å3) |
ρ (gm/cm3) |
vL (km/sec) |
vT (km/sec) |
vm (km/sec) |
θD (K) |
|---|---|---|---|---|---|---|---|
| TiS2 | unpolarised | 62.3411 | 2.9806 | 5.8974 | 3.2766 | 3.6493 | 395 |
| TiS2Cr | unpolarised | 63.6684 | 4.2744 | 6.4531 | 3.5543 | 3.9613 | 469 |
| spin-polarised | 63.6847 | 4.2733 | 7.6282 | 4.5636 | 5.0499 | 598 |
4. Conclusions
A first principles pseudo potential plane wave method has been utilized to explore the electronic structural and mechanical properties of unpolarized TiS2, TiS2Cr and spin-polarized TiS2Cr compounds.
The lattice constant values of unpolarized TiS2 and TiS2Cr compounds are in agreement with the previous theoretical data.
The unpolarized TiS2 and TiS2Cr compounds display metallic bonding whereas spin-polarized TiS2Cr shows directional bonding.
The unpolarized TiS2 and TiS2Cr compounds are associated with ductile behaviour whereas spin-polarized TiS2Cr compound shows brittle nature.
These compounds show anisotropy.
The spin-polarized TiS2Cr shows the maximum value of θD followed by unpolarized TiS2Cr and TiS2.











 nueva página del texto (beta)
nueva página del texto (beta)