1. Introduction

The van der Pol (VDP) oscillator has been studied since almost a century ago, and it is considered a classical prototype of a self-excited oscillator (^{Van der Pol & Van der Mark, 1928}). It has been used to model oscillations in a wide variety of applications such as biological rhythms, heartbeats, chemical oscillations, electrical circuits and circadian rhythms (^{Barron, Medina, & Hilerio, 2014; Nana & Woafo, 2006}). The study of coupled oscillators provides information on emergent properties of the coupled system, such as synchronization, clustering, oscillation death (^{Barron, Hilerio, & Plascencia, 2012}), oscillation modes and stability (^{Ablowitz, 1939}). A common coupling between VDP oscillators that has been examined is that between a pair of oscillators (^{Aggarwal & Richie, 1966; Storti & Rand, 1987; Storti & Reinhall, 2000}). Studies of three coupled oscillator are not common (^{Bakri, Nabergoj, & Tondl, 2007}), and the analysis of four coupled van der Pol oscillators has been tackled by several authors (^{Barron & Sen, 2009; Endo & Mori, 1978; Woafo & Enjieu, 2004}). The analysis of the synchronization of a ring of four identical mutually coupled VDP oscillators by means of the Floquet theory is reported in ^{Woafo and Enjieu (2004)}. The four nonlinear coupled equations of the VDP ring are linearized around the non-perturbed limit cycle and then, by introducing diagonal variables, the linearized equations are changed into a second order homogeneous linear differential equations. Thereafter, by a variable transformation, these equations are converted into a group of canonical Hill equations. Finally, the stability analysis and the synchronization of the VDP ring is carried out applying the Floquet theory. Three domains of stability are reported, and the numerical results are experimentally corroborated in a later work (^{Nana & Woafo, 2006}).

Coupled behavior of VDP oscillators has been studied in the past considering different conditions and applying diverse analysis techniques, for example: diffusive displacement coupling (^{Aggarwal & Richie, 1966}); weak displacement coupling using harmonic balance (^{Linkens, 1976}); weak displacement and velocity couplings using perturbation methods (^{Rand & Holmes, 1980}); strong coupling with detuning using perturbation methods (^{Storti & Rand, 1982}); strong diffusive coupling using matched asymptotic expansions (^{Storti & Rand, 1986}); weak and moderate amplitude coupling with numerical solution (^{Pastor, Perez, Encinas, & Guerra, 1993}); weak and strong bath coupling using the Floquet theory and numerical solution (^{Camacho, Rand, & Howland, 2004; Woafo & Enjieu, 2004}); Whittaker method to determine the synchronized states in a ring of four mutually coupled nonidentical van der Pol oscillators (^{Nana & Woafo, 2006}).

The collective dynamics of large rings of coupled VDP oscillators has been previously analyzed by some of the authors of the present work (^{Barron et al., 2014; Barron & Sen, 2013; Barron, Sen, & Corona, 2008}). In ^{Barron et al. (2008)} the stability and synchronization of a large ring of N coupled identical VDP oscillators under constant coupling parameter distribution is analyzed. In ^{Barron and Sen (2013)} the effect of the singularity of the coupling matrix on the ring dynamics is explored. When this becomes singular, an infinite number of steady states is present, and the phenomenon of oscillation death arises. In ^{Barron et al. (2014)} the collective behavior of a ring of coupled identical VDP oscillators is numerically studied under constant, Gaussian and random distributions of the coupling parameter. Single and multiple coupled frequencies are obtained using the power spectra of the long term time series. In spite of this, many aspects remain to be clarified for large rings of coupled VDP oscillators.

In this work the results reported in ^{Woafo and Enjieu (2004)} and ^{Barron et al. (2008)} are extended to the analysis of the stability and synchronization of a large ring of N coupled VDP oscillators under a sinusoidal distribution of the coupling parameter. Numerical simulations show that for a ring up to one hundred oscillators synchronization and stability are feasible whenever a derived stability condition is satisfied.

2. Mathematical model

The van der Pol oscillator is mathematically expressed as (^{Guckenheimer, Hoffman, & Weckesser, 2003; Van der Pol & Van der Mark, 1928})

(1)

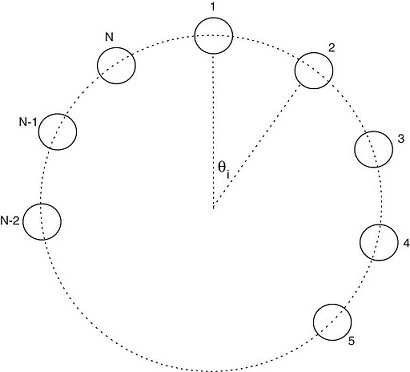
where x is the oscillator position and a is the oscillator constant. In this work, the case of a ring of VDP oscillators in which each oscillator is coupled to its two nearest neighbors is considered. This ring is depicted in Figure 1 (^{Barron & Sen, 2013}). The following expression arises for a ring of N oscillators:

(2)

where 1 ≤ i ≤ N ; b _i is the coupling parameter corresponding to the i th oscillator. If θ _i is the angular position of the i th oscillator, then θ _i = i Δθ , where Δθ = 2π /(N − 1).

Fig. 1 Ring of coupled Van der Pol oscillators (Barron & Sen, 2013). 

A non-uniform distribution of b _i is considered here. Particularly, in the present work, a sinusoidal distribution of b _i is assumed:

(3)

Where B_b is a reference value and A_a is the amplitude of the sinusoidal distribution of b _i.

3. Stability analysis

To analyze the ring stability, the methodology employed in ^{Woafo and Enjieu (2004)} and ^{Barron et al. (2008)} is applied. Full description of this methodology can be found in ^{Barron et al. (2008)}, then just the main results are described and extended here. To linearize Eq. (1) it can be assumed that where, for small values of the oscillator constant In the above equation A is the oscillation amplitude, t is time, ω is the angular frequency and ϕ is the phase shift. Besides, the following diagonal variables can be defined: where δ _i = 1 if i is even and δ _i = −1 if i is odd.

(4)

Where, for small values of the oscillator constant

(5)

In the above equation A is the oscillation amplitude, t is time, ω is the angular frequency and φ is the phase shift. Besides, the following diagonal variables can be defined:

(6)

Where δ_i= 1 if i is even and δ_i = -1 if i is odd.

If the diagonal variables are substituted into the linearized equation of the ring, a second order homogeneous linear differential equation is obtained:

(7)

where τ = ωt − ϕ .

A change of variable defined by (^{Rand & Holmes, 1980})

(8)

is applied to Eq. (7), then this equation is transformed into another one with canonical form of the Hill equation (^{Magnus & Winkler, 1966})

(9)

The stability of the Hill equation can be analyzed by means its periodic or non-periodic terms. Reformulating Eq. (9) as follows (^{Storti & Rand, 1982}):

(10)

Yields the periodic term

(11)

And the non periodic term

(12)

Due to the assumption of a small value of the oscillator constant, the periodic term Q (τ ) can be neglected. Then, the stability of a particular oscillator i and of the whole ring will depend on the sign and value of the non-periodic term. For λ _i > 0, the oscillator and the ring keep their oscillating behavior. For λ _i = 0 the oscillator and the ring cease their oscillations, and the oscillation death phenomenon (^{Barron et al., 2012}) arises. For λ _i < 0, the oscillator and the whole ring become unstable. Then, from Eq. (12), to maintain stable oscillations of the ring the following condition must be satisfied by every oscillator i : Values of the coupling parameter below −0.25, irrespective of the position of a particular oscillator, will cause instability in that oscillator and in the whole ring.

(13)

Values of the coupling parameter below −0.25, irrespective of the position of a particular oscillator, will cause instability in that oscillator and in the whole ring.

4. Numerical results

Eq. (2), which describes a ring of N coupled VDP oscillators, is numerically solved here using the fourth-order Runge-Kutta procedure (^{Chapra & Canale, 2010}). It is assumed that N = 101, which is a sufficiently large amount of oscillators for analysis. Any increase in the amount of oscillators does not change the global behavior of the ring. The time step used for integration is 10⁻⁴, which is small enough to guarantee numerical stability and convergence.

In the numerical simulations, A _b = 1 in Eq. (3) is assumed for the sinusoidal coupling parameter distribution. Besides, the values B _b = 1 and B _b = 0 are considered in the aforementioned equation in order to illustrate the stable and unstable states of the ring, respectively. To analyze the dynamic behavior of the ring, two oscillators are selected for tracking purposes: i = 26 and i = 76, whose corresponding angular positions are θ = π /2 and θ = 3π /2, respectively. The initial conditions are as follows: x (1) = 1, x˙(1)=0, and x (i ) = 0, x˙(i)=0 for 2 ≤ i ≤ N . In order to satisfy Eq. (5) and therefore the validity of the stability analysis, a value of a = 0.1 is assumed in the numerical simulations.

4.1. Ring stability

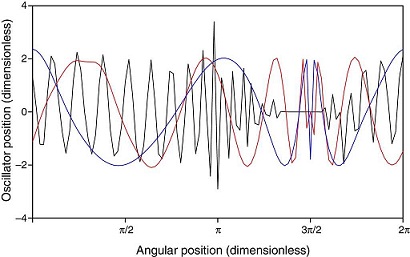
In accordance to Eq. (3), the values of the coupling parameter corresponding to the tracked oscillators for B _b = 1 are b ₂₆ = 2 and b ₇₆ = 0, respectively. The stability condition of Eq. (13) is satisfied by the two tracked oscillators and, therefore, stability of the ring is expected. Initially, wide variations of the oscillation amplitude of oscillator 26 are observed, however for dimensionless times longer than 400 a stable behavior is obtained for both oscillators, as is shown in Figure 2. The long time dynamic behavior of the tracked oscillators is shown in Figure 3, where a constant phase-shift synchronization is observed (^{Pikovsky, Rosenblum, & Kurths, 2001}). Figure 4 shows the position of the ring for times of 100, 500 and 1000. In spite of the changes in the ring position as time proceeds, bounded values of the oscillation amplitudes are preserved, so in this way the stability of the ring is corroborated.

Fig. 2 Dynamic behavior of the tracked oscillators for b₀=1 and A_b=1: i=26 (black) and i=76 (red). 

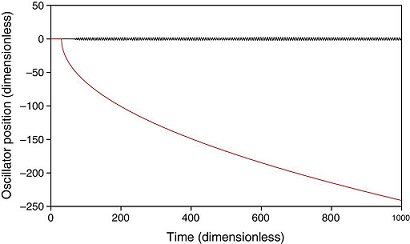
Fig. 3 Long time dynamic behavior of the tracked oscillators corresponding to the simulation of . i=26 (black) and i=76 (red). 

Fig. 4 Time evolution of the oscillators position along the ring for B_b=1 and A_b=1. Times considered: t=100 (black), t=500 (red), t=1000 (blue). 

4.2. Ring instability

The values of the coupling parameter of the tracked oscillators for B _b = 0 are, in accordance to Eq. (3), b ₂₆ = 1 and b ₇₆ = −1, respectively. The stability condition of Eq. (13) is not satisfied for i = 76; therefore, instability of the whole ring is expected. This unstable behavior is shown in Figure 5, where instability is appreciated given that the position of oscillator 76 is increasingly negative. Besides, the time evolution of the ring position for times of 100, 500 and 1000 is depicted in Figure 6, where an ever-increasing amplitude of the ring oscillation in the vicinity of the oscillator 76 is observed. Finally, Figure 7 shows the precise moment in which the position of oscillator 76 becomes boundless.

Fig. 5 Dynamic behavior of the tracked oscillators i=26 (black) and i=76 (red) for b₀=0 and A_b=1. 

Fig. 6 Time evolution of the oscillators position along the ring for B_b=0 and A_b=1. Times considered: t=100 (black), t=500 (red), t=1000 (blue). 

Fig. 7 Instability of the 76th oscillator. 

5. Conclusions

The stable and unstable dynamic behavior of a ring of coupled van der Pol oscillators was studied. Two oscillators were tracked to illustrate the ring behavior. The stability analysis was carried out using previous reported results based on the transformation of the linearized ring equation into a canonical Hill equation. The stability condition was obtained considering the stability of the non-periodic term of the Hill equation. From numerical simulations the following conclusions arise:

Given that the van der Pol oscillator represents oscillating phenomena in a wide variety of practical applications, the results of this work may be potentially useful to analyze the dynamic behavior of coupled rings of many systems and predict their regions of stability and instability.

Conflict of interest

The author has no conflicts of interest to declare.