La variación y las explicaciones didácticas de los profesores en situación escolar

 

Evelia Reséndiz ¹

 

¹ Universidad Autónoma de Tamaulipas México E–mail: erbalderas@uat.edu.mx

 

Fecha de recepción: Abril de 2006
Fecha de aceptación: Agosto de 2006

 

RESUMEN

Esta investigación centra la atención en el papel del discurso en la clase de matemáticas cuando se pretende enseñar conceptos y procesos matemáticos ligados a la noción de variación. El discurso constituye el espacio donde se construyen, negocian e interpretan los significados en la interacción social que se realiza en la escuela, por lo tanto construir conocimiento en interacción requiere del lenguaje usado socialmente. Nos ocupamos de analizar el papel de las explicaciones en la clase de matemáticas, primer semestre de ingeniería, cuando la noción de variación está siendo usada por los profesores y cuando los estudiantes intervienen interactuando con dicha noción. En particular centraremos la atención en los conceptos de función y derivada, vistos en el escrito como modelos para el estudio de la variación. Los registros y las transcripciones de las clases, que se audio grabaron, fueron analizadas considerando un modelo de investigación cualitativa.

PALABRAS CLAVE: Variación, función, discurso, explicación.

 

ABSTRACT

This research focus in the role of the discourse in the mathematics class when intends to teach concepts and mathematical processes connected with the notion of variation. The discourse constitutes a space where are built, negotiate and interpret the meanings in the social interaction that is carried out in the school, therefore to build knowledge in interaction requires of the language used socially. We analyze the role of the explanations in the mathematics class, first semester of engineering, when the notion of variation is being used by the professors and when the students interact with that notion. Particularly we will center the attention in the concepts of function and derivative, seen in the writing as models for the study of the variation. The registers and the class transcriptions were analyzed considering a model of qualitative research.

KEY WORDS: Variation, function, discourse, explanation.

 

RESUMO

Esta investigação centra a atenção no papel do discurso da sala de aula de matemática quando se pretende ensinar conceitos e processos matemáticos ligados noção de variação. O discurso constitui o espaço donde se constroem, negociam e interpretam os significados na interação social que se realiza na escola, assim construir conhecimento em interação requer a linguagem usada socialmente. Nos ocupamos de analisar o papel das explicações na sala de aula de matemáticas, primeiro semestre de engenharia, quando a noção de variação está sendo usada pelos professores e quando os estudantes entrevêem interagindo com tal noção. Em particular centraremos a atenção nos conceitos de função e derivada, observados nas escritas como modelos para o estudo da variação. Os registros e as transcrições das salas de aula observadas e gravadas, foram analisadas considerando um modelo de investigação qualitativa.

PALAVRAS CHAVE: Variação, função, discurso, explicação.

 

RÉSUMÉ

Cette recherche centre son attention dans le rôle du discours en clase de mathématiques lorsqu'il est prétendu d'enseigner des concepts et des procédés mathématiques liés a la notion de variation. Le discours constitue l'espace où se construisent, négocient et interprètent les significations dans l'interaction sociale qui se réalise à l'école, c'est pour autant que construire une connaissance en interaction requière du langage utilisé socialement. Nous nous occupons d'analyser le rôle des explications dans les cours de mathématiques, premier semestre d'ingénieur, quand la notion de variation est utilisée pas les professeurs et quand les étudiants interviennent en interagissant avec cette notion. En particulier, nous centrerons l'attention dans les concepts de fonction et de dérivée, vus dans les documents comme modèles pour l'étude de la variation. Les registres et les transcriptions des cours, qui ont étés audio enregistrés, ont étés analysés en considérant un modèle de recherche qualitative.

MOTS CLÉS: Variation, fonction, discours, explication.

 

INTRODUCCIÓN

Las investigaciones hechas en el campo del aprendizaje del cálculo diferencial e integral se han circunscrito a problemáticas que se ocupan de la matemática en la enseñanza superior, asumiendo que tal asignatura interviene casi exclusivamente como una disciplina central de estudio. Sin embargo, olvidan un hecho fundamental que caracteriza al sistema didáctico de la educación superior: que también –y quizá con mayor fuerza– la matemática escolar está al servicio de otros dominios científicos y otras prácticas de referencia, de las que, a su vez, adquiere sentido y significación. Por el contrario, los estudios sobre pensamiento y lenguaje variacional consideran como una necesidad básica dotar a la investigación de una aproximación sistémica que permita incorporar los cuatro componentes fundamentales de la construcción del conocimiento: su naturaleza epistemológica, su dimensión sociocultural, los planos de lo cognitivo y los modos de transmisión vía la enseñanza.

Aunque la comunicación continúa siendo un tema central en la reforma de la educación de las matemáticas (NCTM, 2000), hay muchas preguntas que deben ser contestadas en relación con el discurso en el aula y los factores que contribuyen al desarrollo del discurso matemático escolar. Las matemáticas, generalmente, se consideran como un cuerpo de conocimiento individual socialmente construido y como un lenguaje especializado para comunicar diversos aspectos de nuestro mundo (Pimm, 1991). Empero, el nuevo saber matemático (individual o compartido) se construye a través de interacciones y conversaciones entre profesores y sus alumnos, de ahí que el movimiento entre el sentido personal de un concepto y el significado matemático compartido resulta crucial para que se lleve a cabo el aprendizaje (Bussi, 1998).

El papel de las interacciones entre el profesor y los estudiantes en tal movimiento enfatiza la importancia de las propias interacciones en el aula y el contenido matemático que se está discutiendo. Por ello, tanto su estudio como el del contenido matemático –o significado compartido de conceptos–influye en el auge de los debates.

Investigaciones diversas en el campo de la Matemática Educativa (García, 1998; Zubieta, 1996; Ávila, 1996; Hoyos, 1996; Cantoral, 1992; Artigue, 1991) señalan que los estudiantes tienen fuertes dificultades al enfrentarse a cuestiones que exigen algún tipo de estrategia variacional. En algunos casos (García, 1998), se ha identificado que los estudiantes de ingeniería –al igual que aquellos reportados en la educación secundaria– todavía no asumen plenamente el objeto "pendiente de una recta" con una totalidad que describe una propiedad de las rectas. Por consecuencia, la noción de derivada, cuyo tratamiento escolar se apoya en la de pendiente, es débil entre los estudiantes.

No es difícil encontrar en diversos diagnósticos hechos que sigue vigente lo que Orton y Dreyfus reportaron en los ochenta: los estudiantes pueden derivar una función, aunque no reconozcan que un cierto problema precisa de un tratamiento que evoca dicha noción. Otros trabajos hacen hincapié –como Zubieta (1996)– en la dificultad de los estudiantes para representar con registros gráficos lo que se les ha comunicado como un enunciado verbal; tal escenario, naturalmente, se extiende más allá de nuestras fronteras. Pulido (1998) y Artigue (1991) analizan las razones por las cuales los estudiantes de ingeniería o ciencias físicas otorgan un significado mínimo a los símbolos comúnmente usados en cálculo, como dx, dy/dx.

Vale la pena aclarar que con nuestro estudio no pretendemos remediar ese estado de cosas; tampoco decir cómo se debe enseñar la noción de variación ni señalar si un profesor enseña bien o mal su clase. Proponemos algo más modesto: comprender el papel que la explicación de la noción de variación juega en la clase de matemáticas en el grado universitario, debido a que genera conocimiento entre profesores y alumnos. Sostenemos que es necesario su cabal entendimiento como punto de partida para cualquier propuesta que intente mejorar la enseñanza del cálculo diferencial e integral en su contexto real.

Ahora bien, pretendemos construir una respuesta, parcial, que centre su atención en algunos fenómenos de enseñanza específicamente involucrados con las dificultades del aprendizaje. De manera particular, hemos centrado la atención en la noción de variación que, si bien no es un objeto explícito de enseñanza, está presente en muchas prácticas discursivas. El uso sistemático de la noción de variación se hace a través de su asociación con conceptos como el de crecimiento y decrecimiento de las funciones, la derivada, los límites, las integrales o las ecuaciones diferenciales, entre otras. Por eso la elegimos como tema de estudio.

Desde esta perspectiva no basta con explorar, por ejemplo, las respuestas que un alumno brinda ante una tarea matemática para saber las causas de su desempeño, sino tendríamos que documentar sistemáticamente y ampliamente las formas en que se comunica y negocia el significado de conceptos y procesos matemáticos en la clase de matemáticas. El presente trabajo pretende contribuir en tal dirección. Para ello, optamos por fijar nuestra atención en el papel que juega la explicación en la clase de matemáticas cuando se intenta enseñar conceptos y procesos matemáticos ligados con la noción de variación, ya que el discurso explicativo es el espacio donde se construyen e interpretan los significados, tomando en cuenta la interacción de naturaleza social que se realiza en la escuela.

La construcción del conocimiento durante la interacción requiere del lenguaje usado socialmente, que en esta investigación describiremos como discurso. De esta forma queremos identificar los elementos discursivos a los que recurre el profesor para realizar su actividad docente, pues el discurso matemático escolar en el salón de clases proporciona un escenario al maestro y a los alumnos con el fin de representar, pensar, hablar, estar de acuerdo o en desacuerdo. Las cuestiones del discurso son abordadas desde múltiples formas, que van del dominio de la lingüística hasta la didáctica (Sfard, 2002, Seeger, 2001, Ball, 1991), las cuales nos explican que el discurso se utiliza para subrayar los modos en que el conocimiento se construye e intercambia en el salón de clases, quién habla, acerca de qué se habla, de qué manera se habla, etc.

Aun son escasas las investigaciones sobre el discurso sostenido en la clase de matemáticas universitarias (Yackel, 2002; Sierpinska, 1994). Por contraparte, en la educación básica está el caso de Pirie (1988), que citan Flores & Sowder (1995), al igual que el de Pimm (1991, 1994), Mopondi (1995), Josse & Robert (1993). Además, el creciente interés por estudiar el papel de los contextos sociales de la cognición ubica al lenguaje como un medio que une lo cognoscitivo con lo social (Carden, 1991). Éste es el caso de los estudios citados en Candela (1990), que exploran la relación entre cultura, lenguaje y cognición y consideran al desarrollo cognoscitivo y lingüístico como una forma de socialización y aprendizaje cultural (Lave 1990, Ochs y Schieffelin, 1994). Otros trabajos conciben al lenguaje como una mediación cultural para el pensamiento y la acción expresados en prácticas cotidianas (Edwards y Mercer, 1987). Piaget (1932) afirmó, por su parte, que la participación de los niños en conflictos sociales tales como las discusiones desarrolla sus habilidades para "ver" con perspectiva, lo cual propicia el crecimiento cognitivo. Vygostsky (1962), en cambio, subrayó el papel del lenguaje social en el desarrollo del pensamiento y, más recientemente, Bishop (1985) enfatizó la importancia de la construcción social del significado para la educación matemática.

La investigación que ahora se reporta estudia la interacción discursiva en el aula desde la perspectiva del profesor. Empero, es pertinente aclarar que no se puede analizar la perspectiva del docente sin considerar a los alumnos, ya que actúan como referentes de sus contribuciones y el significado de éstas depende del contexto interactivo (Reséndiz, 2004).

 

DESCRIPCIÓN DE LA EXPERIENCIA, PARTICIPANTES Y ESCENARIO

A fin de lograr el propósito de la investigación, desarrollamos una actividad sistemática de observación prolongada y análisis que dividimos en dos partes. En la primera, de carácter preliminar, quisimos evaluar la sensibilidad a la observación y al registro que mostraban tanto los profesores de matemáticas de educación superior como sus alumnos en clases, debido a que los procesos de tal índole son completamente inusuales en esos niveles de enseñanza. Así, cuestiones simples de método como filmar, grabar o registrar podrían tener un considerable efecto en nuestros resultados. Asimismo, esta fase sirvió para elegir recursos que no alteraran sensiblemente la dinámica del aula; seleccionamos sólo el audio y registro etnográfico, después de que los profesores aceptaron participar en tales actividades de manera voluntaria.

En cuanto a la segunda parte de la observación sistemática, fue llevada a cabo durante todo un semestre cuando los tres profesores, en cinco grupos, trataban el tema de función y derivadas. Se registró en audio toda la comunicación entre alumnos y maestros, mientras que en notas de observación se consignaron los escritos en el pizarrón, ya fueran del profesor o de algún alumno. Finalmente, al momento del análisis nos ocupamos solamente de tres grupos de Matemáticas I en las carreras de Ingeniería en Sistemas, Bioquímica y Electrónica.

Los participantes en la investigación fueron tres profesores (un físico y dos matemáticos) que impartían la asignatura Matemáticas I en áreas de ingeniería del Tecnológico de Estudios Superiores de Ecatepec. Los profesores fueron seleccionados de manera aleatoria entre los que impartían dicha materia. Se platicó con cada uno de ellos, explicándoles que deseábamos observar y registrar la manera como enseñaban los conceptos de función y derivada, y estuvieron de acuerdo.

Ahora bien, las observaciones se hicieron por un periodo largo sólo en las clases donde se impartieron los conceptos de función y derivada, ya que fueron considerados como modelo para el estudio de la variación. La información se recabó mediante cintas auditivas sobre las discusiones que hubo en el aula durante el semestre, así como notas de campo. Esto permitió contar con una fuente de datos que nos facilitó obtener información tocante a lo que sucede en condiciones "normales" en el salón de clase, al igual que un acercamiento con los profesores y con el grupo, pero sin provocar modificaciones importantes en las formas cotidianas de trabajo y de relación.

 

PROBLEMÁTICA SOBRE LA ENSEÑANZA DEL CÁLCULO

Los temas de función y derivada forman parte del currículo tocante al cálculo diferencial e integral y al análisis matemático. Además, están en un nivel avanzado dentro de la jerarquía de conocimientos matemáticos que se hallan vinculados con temas de matemáticas avanzadas (análisis real, ecuaciones diferenciales, variable compleja), característicos del nivel superior. El énfasis y la profundidad con que se tratan lo establece el perfil de ingreso y egreso del programa de licenciatura en cuestión, aunque cualquier currículo del nivel superior contiene, al menos, un curso de matemáticas con tales temas. En algún sentido, se ha dicho que el cálculo es el paradigma contemporáneo de la educación matemática en el nivel superior (Farfán, 1992; Robinson, 1966), pero constituye a la vez una asignatura con altos índices de reprobación.

En tal sentido, la enseñanza de los principios del cálculo ha resultado siempre problemática (Robinet, 2001). Quizá sea esa la razón por la cual se les enseña a los estudiantes de forma mecánica, haciendo que trabajen con reglas para evaluar funciones o calcular derivadas y que resuelvan problemas típicos. Por ende, la enseñanza tradicional se ha centrado en evaluar habilidades adquiridas en este dominio, que atañen a una práctica algorítmica de naturaleza algebraica para los objetos del cálculo. Si bien este enfoque de enseñanza logra disminuir sustancialmente el porcentaje de estudiantes reprobados, no hace que comprendan de manera satisfactoria los conceptos y métodos del cálculo.

Ahora bien, el cálculo ocupa un lugar primordial en el nivel superior, ya que por sus vínculos tanto con la matemática elemental como su papel en las matemáticas y la ciencia es un conjunto de conocimientos con valor teórico y empírico indispensable no sólo en las ciencias exactas, sino también en las humanidades. No obstante, la enseñanza del cálculo se ha declarado como un problema grave en la educación superior. Cabe mencionar que dicha asignatura se ha convertido en uno de los factores de deserción estudiantil en las instituciones públicas y privadas de educación superior en nuestro país (Albert, 1996). Por otro lado, el cálculo es la herramienta matemática que ha servido para describir los fenómenos de un mundo cambiante; se ha dicho que es la matemática del cambio y la variación (Solís, 1999). Empero, tradicionalmente el cálculo ha sido entendido como el estudio de los procesos inversos de derivación e integración en un contexto simbólico.

 

EL PROBLEMA DE INVESTIGACIÓN

Los estudios sobre pensamiento y lenguaje variacional han sido desarrollados por el grupo de investigación del Área de Educación Superior en el Departamento de Matemática Educativa del Centro de Investigación y Estudios Avanzados del IPN. Dicho grupo ha sostenido, desde sus orígenes, que el actual discurso matemático dominante en las clases de cálculo inhibe el desarrollo de ideas variacionales entre los estudiantes, debido a que la enseñanza de tal asignatura ha sido entendida sólo como un medio para el desarrollo de habilidades algorítmicas, de naturaleza algebraica, que permitan el cálculo de derivadas e integrales, así como su aplicación en problemas de optimización.

Entendemos al estudio del pensamiento y lenguaje variacional como la actividad que se ocupa de los fenómenos de enseñanza, aprendizaje y comunicación de saberes matemáticos propios de la variación y el cambio no sólo en el sistema educativo, sino también en el medio social que le da cabida. De este modo, pone particular atención a los diferentes procesos cognitivos y culturales con que las personas asignan y comparten sentidos y significados, utilizando diferentes estructuras y lenguajes variacionales. Además, es una línea de investigación que tiene una orientación múltiple: por un lado, se ocupa del estudio de estructuras variacionales específicas desde un punto de vista matemático y fenomenológico; por otro, estudia las funciones cognitivas que los seres humanos desarrollan mediante el uso de conceptos y propiedades matemáticas del cambio. Finalmente, toma en cuenta los problemas y situaciones que se abordan y resuelven en el terreno de lo social a través de estructuras variacionales consideradas tanto en la escuela como en el laboratorio (Cantoral, 1997).

Nos interesa comprender las tramas de relaciones entre el profesor, los alumnos y el contenido curricular. Por ello, debido a que consideramos al profesor como el portador del saber que habrá de escenificarse en el aula, llevamos a cabo un amplio estudio sobre las formas de enseñanza que ocupan los profesores al abordar una idea matemática fundamental para el cálculo, pero compleja: la variación. Vamos a abordar ciertas fases de la enseñanza en clase que atañen al profesor; en general, ahondaremos en su discurso oral y en el saber referente a la exposición de conocimientos nuevos (institucionalización).

El objetivo principal de la investigación fue localizar y analizar las maneras en que se introduce y desarrolla la noción de variación en situación de enseñanza en el nivel superior. Así, una forma de abordar el estudio sobre la enseñanza de la variación es mediante el discurso en el aula, donde la palabra se utiliza la mayor parte del tiempo. La comunicación y, específicamente, la interacción entre docente–alumno y alumno–alumno se considera en la actualidad como la base de proceso de aprendizaje (Tusón & Unamuno, 1999). Una de las maneras de tener acceso a la información sobre cómo se introduce y se desarrolla la noción de variación consiste en estudiar el discurso del profesor, pero también el tocante a la interacción social, que se realiza en el aula. Por lo anterior, el problema de investigación se delimitó con las siguientes preguntas: ¿Cuál es el papel que juega la variación en el discurso del profesor? ¿Qué sucede con la noción en la interacción?

Para intentar responder a dichas cuestiones, es necesario desarrollar perspectivas teóricas que sean útiles para interpretar y analizar la complejidad de las clases de matemáticas. Además, los profesores cotidianamente reconstruyen su trabajo docente con experiencias, estrategias y prácticas que asimilan, acomodan, rechazan, modifican o aceptan en su interacción con los alumnos.

 

ASPECTOS TEÓRICOS Y METODOLÓGICOS

Para realizar las observaciones, nos apoyaremos en un punto de vista teórico: el de las situaciones didácticas y la transposición didáctica.

Brousseau (1987) desarrolló la teoría de situaciones didácticas, que engloba al conjunto de relaciones expresadas en el salón de clase entre el docente, los alumnos y el conocimiento; asimismo, pretende modelar y contrastar empíricamente los fenómenos didácticos que surgen en el ámbito escolar. Las representaciones que el profesor tiene de la enseñanza y del aprendizaje influyen en su quehacer y en la elección de su estrategia, modificando el saber que entra al aula. Estas transformaciones son determinadas por relaciones casi siempre implícitas, reguladas por lo que Brousseau (1990) llamó contrato didáctico, al cual define como el conjunto de relaciones implícitas que regulan el funcionamiento de la clase de matemáticas y las interacciones entre el maestro y los alumnos.

Como en la comunicación de un saber a un público determinado se origina la modificación de tal conocimiento, al proceso en el que un saber pasa hacia un sitio didáctico se le denomina transposición didáctica (Chevallard, 1991). En sentido amplio, es un proceso con un desarrollo más complejo, donde intervienen múltiples aspectos: en primer lugar, el profesor ha de adaptar sus propios conocimientos a los objetos a enseñar, luego debe instalarlos en el saber escolar y, por último, organizarlos temporalmente. Por ende, necesita realizar una transición del saber escolar al saber enseñado, teniendo en cuenta que este último nunca es totalmente retenido por el estudiante sino que, a través de la relación didáctica entre profesor y alumnos, se convierte en saber del alumno. En dicha relación didáctica interesa, para nuestra investigación, dar cuenta de los recursos discursivos que se usan –por parte del profesor, mas influenciados por los alumnos– y construyen en la interacción respecto a la noción de variación.

Un fenómeno importante a observar, ligado al control de la transposición didáctica, consiste en el envejecimiento de las situaciones de enseñanza, cuyos patrones de interacción aluden a las relaciones entre el profesor, los alumnos y las propias situaciones. Se ha podido dar cuenta en este estudio de tal fenómeno didáctico al interior del aula, pues en la interacción se modifican las situaciones de enseñanza del profesor; así, cuando hay interacciones cambian las relaciones de poder y las situaciones de enseñanza.

En nuestro caso, analizamos un fenómeno didáctico en el campo de la matemática universitaria, usando la aproximación sistémica que brinda la didáctica de la matemática como disciplina científica. Aunque podíamos explicar las interacciones entre los polos del saber, el profesor y el alumno con base en las nociones de contrato, situación o transposición, quisimos profundizar en el papel del discurso en el aula, razón por la cual incorporamos elementos de los estudios cualitativos de corte etnográfico. Los análisis y la discusión del trabajo han implicado interpretaciones y análisis en direcciones específicas; tal proceso concluye cuando se han formulado explicaciones sólidamente fundamentadas en los datos.

Dada la posición teórica de nuestro trabajo, anclada en las situaciones didácticas (donde se destaca que la situación de aprendizaje propicie una serie de interacciones que hagan funcional la comunicación y el intercambio de ideas, llevando a la construcción de un conocimiento) y la transposición didáctica (fenómeno ligados con su control, ya que a través de la relación didáctica entre el profesor y los alumnos el saber enseñado se convierte en saber del alumno), la perspectiva etnográfica resultó la más adecuada.

El enfoque etnográfico permite obtener información relevante sobre el contexto de la clase, lo cual resulta notable para la interpretación. Tal perspectiva admite que se realice un detallado estudio secuencial sobre las situaciones de enseñanza, a fin de describir el trabajo que se hace en cada intervención que antecede o precede a otra situación de enseñanza. Este nivel de detalle, sin perder el contexto general de cada clase impartida en cada aula escolar particular, es en nuestra opinión el que reconstruye el sentido que tienen las intervenciones para los participantes.

Habitualmente, los análisis de matemática educativa en el contexto superior se llevan a cabo al intervenir en el sistema de enseñanza con el diseño de una situación de aprendizaje, o con un vasto dispositivo de ingeniería didáctica. En ambos casos, la intervención sucede desde el diseño de la actividad y su puesta en funcionamiento es controlada desde fuera del aula. El investigador, a quien suele considerarse en este modelo como un verdadero ingeniero di dacta, participa en la concepción, diseño, implantación y análisis de la puesta en escena, determina las variables de control y, a través de ellas, regula su mediación en el sistema de enseñanza.

Como el enfoque etnográfico, a diferencia del anterior, disfruta de la contemplación y no pretende participar al momento de la observación ni tiene como objetivo la intervención, nuestro primer reto fue buscar una articulación adecuada entre estas aproximaciones. Tuvimos que coordinar, en el campo teórico, el estudio del envejecimiento con el del análisis de las explicaciones en aula, cuando el docente introduce la noción de variación. Abandonamos la aspiración de diseñar una situación didáctica con fines de intervención, razón por la cual no seguimos la metodología típica de las situaciones didácticas (acción, formulación, validación e institucionalización), sino tratamos el fenómeno de envejecimiento que se da en la etapa de institucionalización.

Por último, recordamos que la teoría de situaciones de Brousseau (1986) se basa en una aproximación constructivista, la cual actúa bajo el principio de que una noción se construye en el ambiente de situaciones de enseñanza, creando un discurso hecho tanto por el maestro como por los alumnos. Si bien en un principio consideramos sólo las explicaciones del docente, tuvimos que cambiar nuestra óptica, pues observamos que los alumnos desempeñaban un papel central en el discurso de la clase; así, el docente no es la única, ni siquiera la principal fuente de autoridad matemática. Los alumnos comparten sus respuestas con el docente y sus compañeros.

 

LAS EXPLICACIONES EN LA CLASE DE MATEMÁTICAS

Si se concibe a la enseñanza como un espacio de comunicación, el discurso es el vehículo que transporta la mayoría de los aprendizajes surgidos en el salón de clases, ya que sus aspectos están poblados de diferentes lenguajes que unos emiten y otros intentan interpretar correctamente. Idealmente, el aula conforma un espacio para el entendimiento mutuo, para cierta negociación de conocimientos y para la formación de significados compartidos; en tal sentido, enseñar consiste fundamentalmente en comunicar (Edwards y Mercer, 1987). Dicho enfoque sugiere que se analice aquello que se dice y cómo se dicen las cosas dentro de la clase.

Al considerar al discurso como un medio para estudiar las prácticas sociales (Candela, 1999), partimos del hecho de que el discurso en el aula tiene una organización explicativa, pues toda intervención se puede ver orientada hacia la comprensión de alguna idea, noción o concepto. Para estudiar el discurso de los profesores, fue conveniente prestar atención a algunas situaciones del aula donde se emplean una serie de explicaciones didácticas (en el sentido de Sierpinska, 1994) y de recursos discursivos para hacer asequible la noción de variación; por ello, analizamos el papel de las acciones explicativas en la construcción de significados y la forma y situaciones donde los profesores ocupaban tal recurso. Sin embargo, nos ha interesado también estudiar las prácticas discursivas en la interacción dentro del aula para indagar el papel de la explicación en la construcción del conocimiento en el contexto escolar. Consideramos que uno de los objetivos del docente es hacer comprender a los estudiantes los conocimientos matemáticos o los saberes que enseña; entre los esfuerzos que el profesor lleva a cabo figuran las explicaciones.

Por explicación se entiende aquellas partes del discurso que tienden a hacer comprender una noción, idea, hecho, objeto o fenómeno, pero van más allá de su descripción, ya que tratan de encontrar las causas que lo provocan o permiten entenderlo. La explicación no sólo consiste en una actividad reflexiva en relación con otra, sino también es un medio explícito del que dispone el profesor o el estudiante para unir o enlazar las ideas; además, ofrece una o más razones para volver comprensible un dato, fenómeno, resultado o comportamiento (Duval, 1999). Entonces, la explicación constituye uno de los medios que utiliza el profesor para hacer comprender o "dar sentido", se convierte en el objeto de una comunicación, de un debate o de una discusión; puede aparecer como una comunicación de información útil o como un medio para facilitar rápidamente una comunicación o argumentación.

El profesor asume explícitamente la responsabilidad de "hacer comprender" y de establecer vínculos con sus alumnos a través de sus explicaciones, que pueden tener diversos estatus didácticos: simples comentarios, ilustraciones, soluciones de problemas, demostraciones, entre otros.

Por otra parte, nos interesa poner en tela de juicio la concepción de que en el salón de clases los discursos son autoritarios y los formatos comunicativos que usa el docente se caracterizan por su rigidez y poca reflexión, sin atender a la manera en que llega la información a los alumnos. Esto se debe a que los conocimientos ya están acabados y son congruentes con los planes de educación superior, de ahí que al docente se le atribuya la autoridad de ser el conocedor de la verdad. Empero, veremos las explicaciones del docente y cómo son modificadas cuando mantiene una interacción discursiva con los alumnos.

Anteriormente, se estudiaban aspectos relativos a la personalidad y características del profesor, a quien se le concebía como un profesional que no sólo actuaba, sino también reflexionaba sobre la educación; por consiguiente, era capaz de generar conocimientos. A esta perspectiva se le conoce como paradigma del pensamiento del profesor. Sin embargo, en la actualidad hay trabajos que abordan el discurso sostenido en la clase de matemáticas. Nuestra tesis puede aportar algunos elementos que abrirían la posibilidad de analizar el discurso docente en la interacción social.

Sierpinska (1994) hace una diferencia entre las explicaciones científicas y las explicaciones didácticas. El objetivo de las primeras consiste en lograr el entendimiento de bases más conceptuales –por ejemplo, de una teoría matemática abstracta–, mientras que las segundas se dirigen a un entendimiento con bases más familiares (una imagen, algún conocimiento previo o experiencias) y frecuentes en la enseñanza. Como el rol de la explicación radica en volver asequible el sentido de un objeto, ya sea método, término o enunciado, es el medio que utilizan el docente y los estudiantes para mostrar o investigar la comprensión. Sus fines son variados: enseñar, convencer, requerir un orden u obtener una ventaja.

Hay una gran diferencia –tanto de rol como de forma– entre las explicaciones que el profesor da a los estudiantes, las que proporciona un estudiante a su profesor y las que ofrecen los alumnos a sus compañeros. Estas clases de explicaciones se subdividen de acuerdo con los objetivos de las situaciones, como la explicación de una consigna, un error, una ausencia o un teorema, o bien aquellas que pueden ser propuestas, impuestas o solicitadas. Todas constatan las diferencias o asimetría en el uso del lenguaje.

 

ANÁLISIS Y RESULTADOS

La variación y las explicaciones didácticas de los profesores

En esta investigación nos interesa mostrar cómo aparece la noción de variación en la enseñanza y cuál es su desarrollo en el proceso de negociación de significados del discurso en el aula.

Sierpinska (1994) y Mopondi (1995) apuntan que las explicaciones didácticas son aquellas que ofrece el profesor o el alumno, y se dirigen a un entendimiento con bases más familiares y frecuentes en la enseñanza. Ofrecen una o más razones para volver comprensible un dato, fenómeno, resultado o comportamiento (Duval, 1999).

Para que pudiéramos estudiar los recursos o elementos discursivos de que se valen los profesores al abordar la noción de variación, dirigimos nuestro análisis hacia las situaciones donde explican con claridad sus diferentes temas de estudio, función y derivada; también atendimos a las explicaciones de los alumnos, sus demandas de una mayor exposición y cómo se modifica la explicación durante la interacción. Para ello, optamos por enfocar nuestra atención en el papel de las explicaciones durante la clase de matemáticas, cuando se pretende enseñar conceptos y procesos matemáticos ligados con la variación.

De este modo pretendemos identificar las explicaciones didácticas, los elementos discursivos y la negociación de significados a los que recurre el profesor, tomando en cuenta que el discurso matemático escolar en el salón de clases proporciona un escenario para el maestro y los alumnos a fin de que representen, piensen, hablen, estén de acuerdo o no.

Aquí se sugiere un análisis sobre qué y cómo se dicen las cosas durante la clase, bajo la premisa de que el discurso en el aula tiene una organización explicativa, pues toda intervención se puede ver orientada hacia la comprensión de alguna idea, noción o concepto.

Un primer asunto que nos interesó explorar fue el concerniente a las ideas que tenían los docentes sobre la noción de variación, con base en las explicaciones que formularon en el salón de clase y cómo se modificaron en la interacción discursiva para llegar a acuerdos. Algunas secuencias discursivas fueron cortas y otras un poco más largas; sin embargo, como la interacción que se genera en el aula hace complicado recortar y elegir sólo la explicación del docente, resultó muy difícil mostrar ejemplos de todos los puntos considerados.

En las explicaciones que dan los profesores, la noción de variación desempeña los siguientes papeles:

• Cuando emplean la tabulación como variación numérica.

• Al momento de construir gráficas, como la variación de un punto de referencia.

• En sus expresiones verbales con referencia a situaciones cotidianas.

• Mediante el empleo de parámetros como variables principales.

• En los casos donde la derivada es vista como covariación o comparación a/b.

 

La construcción de explicaciones

Debido a su carácter interactivo, la construcción de explicaciones vista como objeto de análisis implica que sus unidades mínimas sean secuencias de interacción, no frases o mensajes descontextualizados (Candela, 1999), pues hay que atender a la construcción de los recursos discursivos y los significados sobre la variación.

Ahora bien, consideramos como unidad de análisis natural a la clase completa en la que se delimita y trabaja el contenido de un tema curricular dentro de la jornada escolar, mientras que seleccionamos como secuencias discursivas a aquellas donde se pudieran identificar las actividades y las explicaciones de los profesores frente al contenido en que aparece la noción de variación. Los extractos forman parte de las clases o sesiones de un primer semestre de ingeniería. A continuación, mostramos un ejemplo en el que la explicación del profesor se centra en el desplazamiento del vértice.

Un primer acercamiento a la noción de variación en el aula es por medio de la tabulación. En las explicaciones de los profesores está la idea de relación entre conjuntos, comportamiento de los puntos intermedios, aproximación, rotación, crecimiento o decrecimiento.

 

Extracto 5.2

P: La forma más simple para trazar una recta y=2x+3 necesita ¿qué cosa? ¿Cuál es el requisito mínimo para trazarla?

Am: Dos puntos.

Am: Que tenga dos puntos.

P: Dos puntos. Entonces, según el axioma de la geometría, para trazar una recta es suficiente tener dos puntos. Y para un plano, ¿cuántos puntos se necesitan?

Am: ¿Para un qué?

Am: Cuatro.

P: Un plano.

Am: Cuatro.

Am: Tres.

P: Tres puntos definen un plano, dos son suficientes para trazar una recta. Yo no puedo trazar una recta si no tengo dos puntos, con uno no puedo hacer nada, un plano requiere de tres. Necesito dos puntos para trazar la recta, y los más simples para trazarlos son donde cortan el eje de las X's; es decir, cuando X vale 0, ¿cuánto vale Y?

As: 3.

P: Cuando Y vale 0, ¿cuánto vale X?

Am: 2.

P: ¿Cuánto dijeron?

Am: ¿Cuando X vale cuánto?

P: Cuando X vale 0, Y vale 3, ese es uno. Cuando Y vale 0, ¿cuánto vale X ? ¿Se dieron cuenta de dónde lo sacamos?

As: ¡Sí!

P: ...No necesita ser tanto. Simplemente dos puntos son suficientes para cruzar la recta ¿Cuáles? Los que cortan el eje de las X's [...] Si no lo entendieron [...] si alguno de ustedes dice, 'bueno, pues yo no le creo mucho al maestro, pero mejor voy a hacer mi tablita', pueden hacer la tabulación y ya pueden trazar y=2x+3.

En esta sesión, el docente ofrece una explicación de la función constante, lineal, así como de la cuadrática en forma polinomial de cada una de las funciones. Luego sugiere un ejemplo de la función lineal y=2x+3 y pregunta a los alumnos cuál es el requisito mínimo para trazarla. Ellos responden que dos puntos.

Para localizar un punto en el plano se requiere de dos números. Sabemos que cualquier punto puede representarse como un par ordenado (a, b). El docente pregunta: ¿Y para un plano cuántos puntos se necesitan? Un alumno responde por medio de otra pregunta: ¿Para un qué?, demandando una explicación; sin embargo, otro alumno afirma que tres puntos.

El profesor sugiere a la tabulación como medio para validar la gráfica, ya que afirma que dos puntos son suficientes para trazarla, mas pone en duda su explicación cuando les dice a los alumnos que entonces hagan la tabulación si no le entendieron o no le creen. El profesor justifica los resultados o el método empleado (que va a institucionalizar) e intenta validarlo.

La explicación del maestro usa el modelo de la tabla de valores, donde se muestra la relación que hay entre dos cantidades. La noción de variación que se puede ver durante la clase es la numérica, pues el modelo o representación consiste en la tabla de valores y, por último, se aborda el modelo geométrico.

Aquí se aprecia una situación didáctica donde se dan un conjunto de relaciones, surgidas al interior del salón de clase, entre el docente, los alumnos y el conocimiento; dichas relaciones nos interesa estudiar, ya que son de tipo explicativo. El profesor explica al alumno con base en el millieu, haciendo uso de todos los elementos a su alcance; en este caso, el modelo de la tabla de valores, aunado al modelo geométrico de la recta. Tal hecho será una característica notable en el fenómeno de envejecimiento. Se acude a los recursos disponibles para intentar cambiar la explicación.

En las explicaciones de los tres profesores aparece la idea de mover un punto de referencia como el origen, el vértice o la asíntota, que fue de gran importancia para construir o elaborar las explicaciones acerca del movimiento de la gráfica. En la secuencia siguiente, la explicación del profesor gira en torno al desplazamiento del vértice o a la variación de un punto de referencia.

 

Extracto 5. 15

P: Bueno, ¿cuál es gráfica de la función si le sumamos, por ejemplo, 1, y queda y=x²+1?

Am: Se desplaza el origen en y=1.

P: ¿Verdad que estaríamos haciendo eso? Dijera que y va a ser lo que valga en x² y eso que estaríamos haciendo sumándole 1, ¿dónde está en x? En 0 pónganle 1, en 0 pongo 1 y en 1 cuando valga 1, ahora la y ¿cuánto va a valer?

As: ¡2!

P: Va a valer 2 [...] y entonces la fórmula seguiría siendo la misma. ¿Qué fue lo único que sucedió? Que la curva se desplazó una unidad hacia arriba y si la quisiera yo bajar ¿qué podríamos hacer?

As: ¡Restar!

P: Restarle 1. ¿Ahora cuál sería la gráfica de y=x²–1? Le podemos poner esta y=x², y si regresamos 1 ¿qué va a suceder? Cuando abres al vértice el (0,–1) donde corta al eje x en 1,–1, y esta es la gráfica de y=x²–1, de y=x². Si yo le resto, ¿qué sucede con la curva?

Am: La desplazamos.

P:¿Cuántas unidades la desplazamos?

Inicia la explicación con la función cuadrática básica y=x² que, cuando se le suma una unidad (y=x²+1), desplaza su origen en y=1. La afirmación se desplaza el vértice en y=1 fue hecha por un alumno, aunque no se le solicitó. Al restarle una unidad a la función cuadrática básica (y=x²–1) se desplaza el vértice una unidad hacia abajo y al sumarle una va hacia arriba. El docente utiliza el término desplaza que expresó el alumno cuando asevera: la curva se desplazó una unidad hacia arriba.

Cuando el profesor demanda que los alumnos expongan su opinión, a través de preguntas motiva intervenciones explicativas y resulta de sumo interés para los alumnos poder "mover" o "desplazar" el vértice de su posición inicial. El profesor intenta generalizar que, si a la función básica le suman una cantidad, la gráfica se desplaza hacia arriba; si le restan, hacia abajo. En tal situación hay dos tipos de explicación donde interviene la noción de variación: el modelo del lenguaje natural y el modelo de la representación geométrica, que sirve para visualizar los movimientos.

Enseguida, veremos cómo se desplaza el vértice de una función cuadrática básica (y=x²) cuando se le suma una unidad y se eleva al cuadrado y=(x+1)².

 

Extracto 5.16

P: Es una parábola Y=(x+1)². Inclusive hasta la podemos ver así, y=x²+2x+1, ¿verdad? Luego, el –2 ¿cuánto es? El –2 es 1. Entonces, la curva sería así –a ver si estamos de acuerdo–, mientras que la forma básica sería hasta acá, que es y=x²; la forma sigue siendo la misma. Debemos entender que es la misma curva y lo único que hace la línea es desplazarla, ¿hacia dónde?

Am: A la izquierda.

P: Hacia la izquierda. Y si la quisiéramos mover más hacia la izquierda, ¿qué tendríamos que hacer? Que se sustituya en la forma básica ¿a quién? A x por x+2 (y=(x+2)²). Si la quiero yo hacia la izquierda, hasta –10, entonces ¿en dónde se ubicaría F? Si la función original es f(x)=x² y yo me la quiero llevar hasta el vértice que está en –10, ¿qué hago?

Am: Sería: y=(x+10)²

La explicación del profesor toma como referencia a la función básica. Es la misma forma de la curva, pero ahora se desplaza una unidad hacia la izquierda y, si se quiere mover más, se tendría que dar un número negativo cualquiera, como –10. Al término de las explicaciones sobre el movimiento o el desplazamiento del vértice, el docente resume el tema con la siguiente tabla.

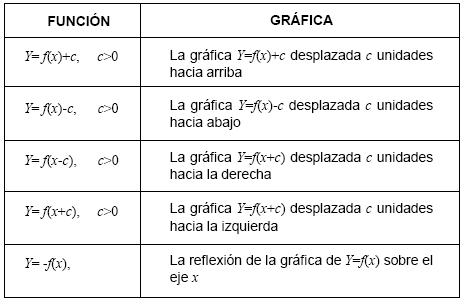
Se aprecian dos tipos de explicación que implican la noción de variación. Uno es el modelo del lenguaje natural (desplazamiento hacia arriba, hacia abajo, izquierda, derecha); otro, el de la representación geométrica, que permite visualizar el desplazamiento de la gráfica o parábola.

Durante la sesión de funciones trigonométricas, el profesor aborda las relaciones trigonométricas y pregunta qué significan tales relaciones o números (cateto opuesto dividido por la hipotenusa, por ejemplo). Un alumno responde que son como razones de cambio y el docente la retoma debido a que no le convenció; argumenta que, cuando se habla de cambio, se alude a una variación de cociente a la que cual también se le llama razón, pero no se gana nada, sólo cambia el nombre. La razón entre cateto opuesto y la hipotenusa es la relación trigonométrica seno.

 

Extracto 5.21

P: 0.5, seno de 60°, cateto opuesto dividido por la hipotenusa y esto nos da 0.8660, pero tenemos la misma pregunta, ¿qué significa? Yo sé calcular esto y si no lo sé, la calculadora lo hace; nada más se le aprietan algunas teclas. Sin embargo, me interesaría contestar esa pregunta: ¿qué significan esos números?

Am: Son como razones de cambio.

P: Sí. Cuando uno habla de cambio, habla de variación de cociente, o sea, es una razón, pero no ganamos nada porque entendemos que es un cociente, al que también se le llama razón. Únicamente le estamos cambiando nombre, ¿verdad? Lo que dice su compañero no lo podemos negar. Sí es cierto que esta es una relación a través de la razón, como una división, ¿están de acuerdo? Es la razón entre estos lados... entre los catetos, perdón... la razón entre el cateto opuesto y la hipotenusa, y el cateto opuesto y la hipotenusa da la relación trigonométrica seno. El seno consiste en la relación que guarda el cateto opuesto con la hipotenusa; la razón que guarda es como agarrar una naranja y decir 'la voy a dividir entre dos personas'. ¿Cuál es la razón de una naranja con relación a estas dos personas? Sería tomar la naranja y dividirla entre dos: media naranja...

Para convencer a los alumnos de la razón que guarda el cateto opuesto y la hipotenusa, el docente formula una analogía: Es como agarrar una naranja y decir 'la voy a dividir entre dos personas'. ¿Cuál es la razón de una naranja con relación a estas dos personas? Sería tomar la naranja y dividirla entre dos: media naranja. Intenta explicar una situación poco familiar comparándola con otra similar, mas poco conocida por los alumnos, para que puedan comprender y compartir la explicación.

La explicación del docente se basa en una supuesta variación del cociente, que ejemplifica o relaciona con otra idea en la cual recurre, un poco forzado, al empleo de expresiones que considera serán familiares para el alumno. En esta relación didáctica típica del aula que hemos estudiado el profesor, al buscar "disminuir" o "invalidar" de alguna manera la intervención del alumno y conservar su carácter de guía en el debate, utiliza este argumento inconsistente con el problema, pues no se trata de un cociente cualquiera, sino de un cociente de incrementos; es decir, la razón de los cambios. Digamos que explica sin explicar. La participación del alumno en este sentido logró la emergencia de una metáfora, lo cual nos lleva a considerar que las interacciones entre alumnos y maestro regulan el envejecimiento de las situaciones de enseñanza, ya que las modifican. Sin dicha intervención, el profesor simplemente habría definido el concepto.

En el siguiente fragmento veremos la explicación del docente cuando resuelve un ejercicio que dejó como tarea. Consisteen graficar las funciones cuando varían los parámetros f(x)= sen x, f(x)= sen 2x, f(x)= 2senx, y hallar algunas diferencias y similitudes entre ellas.

 

Extracto 5.26

P: ¿Cómo quedaría la función? A ver, la primera función es f(x)= 2sen x, ¿verdad? Bueno, aquí dice que el doble del seno de 0 es 0; el doble de π / es 2 y el doble del seno de π es 0. Si ustedes se acuerdan de la función que trazamos al principio, la senoidal, encontramos que la primera era de este estilo, ¿verdad?, donde solamente andaban entre 1 y –1. Si ustedes observan tenía –1 y 1; esa era la oscilación que tomaban los valores del rango. Van a ver ustedes qué le pasa al doble: aumentó al doble. Es decir, la función se duplicó; si fuera triple, entonces la función sería tres veces más; si fuera 4 ó 5 veces va aumentando su amplitud.

Am: ¿Es una onda, maestro?

P: Es una onda central.

Am: Maestro.

P: Bueno, nada más que va aumentando la amplitud. Lo que sale aquí es más, ¿no? Sería esto, perdón, es así entonces, ¿verdad? Porque π / 2 es 1, entonces es 1: aumenta el doble. Eso es lo que quería que observaran. La otra es la función seno doble, que dice: seno del ángulo doble, es decir, dos veces el seno de 90, dos veces el seno de 0, dos veces el seno de 180, dos veces el seno de 270 o dos veces el seno de 360. ¿Qué pasa ahora con la función? ¿Qué pasa con la función f(x)= sen 2x?

Am: Donde era una frecuencia ahora son dos frecuencias.

Su exposición inicia con la función básica f(x) = sen x, que oscila entre –1 y 1, y la toma como referencia. Posteriormente, atiende al cambio que sufre cuando es multiplicada por 2: aumenta al doble, se duplica. Un alumno, al ver la forma de la gráfica, pregunta: ¿Es una onda, maestro? para conocer si se sigue conservando la onda. El docente responde que se trata de una onda central.

La última función es f(x)= sen 2x, seno del ángulo doble, apunta el docente, y formula la siguiente pregunta: ¿Qué pasa con la función f(x)= sen 2x?. Un alumno responde: Donde era una frecuencia ahora son dos frecuencias. Aunque el docente sabe que tal respuesta es correcta, no la valida inmediatamente y prosigue a dar algunos valores de ángulos para evaluar la función y llegar a la respuesta deseada.

El profesor intenta generalizar su explicación, al decir que la gráfica tendrá cierto comportamiento de acuerdo con los parámetros. Si la función la multiplica por 2, se duplica, y si se hace por 3, aumentaría 3 veces, y así sucesivamente, pues el valor al que se multiplique la función modificará su dominio y rango: los parámetros funcionan como un todo. La función básica f(x)=sen x juega un papel importante para graficar las funciones propuestas.

La explicación del profesor sobre la noción de variación fue construida bajo el modelo de representación gráfica, y con la manipulación de los parámetros hizo visibles los cambios de la gráfica.

El profesor Bruno explica la pendiente y posteriormente define la derivada.

 

Extracto 5.28

P: En este triángulo rectángulo, ¿cuánto miden sus catetos?

As: x₂–x₁

P: x₂–x₁. ¿Cuánto mide el cateto que está abajo?

As: y₂–y₁

P: Es y₂–y₁ , de donde me resultaría que la pendiente de esta recta va a ser igual a la tangente trigonométrica del ángulo de inclinación, y yo tengo ahí que la pendiente es ¿qué?

As: [...]

P: Es y₂–y₁. Si les digo la situación que me motiva a eso, ¿está bien? ¿Por qué?

Am: [...]

P: Porque si invertimos tanto el numerador como el denominador, dice su compañero, van a cambiar de signo y el resultado del cociente va a ser negativo. Si aquí la diferencia apunta que ambas son positivas, el cociente va ser positivo y, al invertirlo, si me salieron allá dos positivos, va a ser negativo. Ambos cocientes van ser positivos, ¿estamos de acuerdo?

El docente basa su explicación en un triángulo rectángulo y hace la pregunta ¿cuánto miden los catetos? para generar la interacción con los alumnos. A continuación, escribe la fórmula de la pendiente y pregunta si el orden de las variables es correcto; un alumno respondió, aunque no se escuchó su intervención en el audio. Por el comentario del profesor, si invertimos tanto el numerador como el denominador, dice su compañero, van a cambiar de signo, alude al cambio en el orden de la fórmula.

Dicha explicación es una clara comparación de los valores del cociente: si cambia el numerador como lo hace el denominador. Aunque su discurso es un poco confuso, el docente llega a decir que los dos cocientes serían positivos, ya que negativo entre negativo da positivo. Por ende, la explicación del profesor se apoya en el triángulo rectángulo y establece una comparación a/b, donde le da significado al cociente de variación.

 

La explicación y el contexto institucional

En el salón de clases surgen diversas alternativas explicativas sobre los temas abordados. Tanto el profesor como los alumnos intentan construir versiones del contenido escolar a partir de su propia óptica. Los participantes aportan sus explicaciones para entender y poder orientar los acuerdos entre ellos, situación que se produce frecuentemente con base en los contextos profesionales de la especialidad de la ingeniería que se estudie, o bien en la especialidad relativa a la experiencia profesional del docente fuera del aula.

Por ello, la explicación del profesor se nutre fuertemente con expresiones cotidianas de un campo disciplinario específico, abandonando en cierta medida el discurso tradicional de una clase de matemáticas. Este tipo de recurso fue empleado de manera consistente en los episodios que analizamos.

Un aspecto importante en la formulación de explicaciones por parte de los docentes ha sido la necesidad de situarse en contextos donde puedan hacer aplicaciones que atañen a la carrera de sus alumnos, como se mencionó en el capítulo anterior. La cultura matemática escolar no alude exclusivamente a los acuerdos sociales alcanzados ni a los consensos construidos por una cierta comunidad didáctica, ya que precisan de niveles de institucionalización que vinculan el saber escolar con su correspondiente saber erudito.

Lo cultural, en el caso que nos ocupa, implica que aquello que se aprende esté cerca de lo que da significados. Entonces, lo significativo del conocimiento estará asociado tanto al contexto donde se presenten las explicaciones como a la estructura matemática de los conceptos. A continuación, mostraremos algunas secuencias ilustrativas al respecto.

En el siguiente fragmento, el profesor explica un ejemplo que abordó en otro grupo de primer semestre de Ingeniería en Electrónica, donde la función representa una señal eléctrica o electromagnética, magnética o acústica, a la cual le llama onda, mientras que donde se mueve un punto (desfasamiento) es la variación de un punto de referencia (vértice).

 

Extracto 5.34

P: Hace en momento estaba trabajando con los muchachos que quieren estudiar Ingeniería en Electrónica y nosotros a esto le llamamos desfasamiento (ftx)=(x+ l)²). Para nosotros, esta función representaría una señal eléctrica, electromagnética, magnética o acústica, e indistintamente la llamamos onda. Algunos estamos familiarizados con las ondas eléctricas y esta es una onda. Entonces, yo pongo un ejemplo y digo: 'esta expresión matemática representa una onda'. Ahora, la pregunta es: ¿hacia dónde se mueve la onda?

As: ¡Hacia la izquierda!

P: Hacia la izquierda. Entonces, el ingeniero ya sabe hacia dónde se mueve la onda viendo una ecuación matemática, fíjense. Él ya sabe lo que ocurre en la naturaleza con el uso de una simple ecuación matemática.

El docente pregunta sobre la dirección del movimiento de la onda y la mayoría de los alumnos responde: ¡Hacia la izquierda! Para el profesor resulta evidente que el ingeniero ya sabe hacia dónde se mueve la onda con la observación y análisis de una ecuación matemática, pues conoce el papel de una ecuación matemática como modelo de la naturaleza. Con tal comentario, da por hecho que los ingenieros reconocen inmediatamente esa particular interpretación de las funciones.

Aquí se presentan dos tipos de explicación en las que aparece la noción de variación: el de la representación gráfica y el del lenguaje natural del desfasamiento. En el extracto siguiente, el profesor se sitúa en el contexto (comienza a decir cómo utiliza el físico esto, ya que él tiene esa formación) y les pregunta a los alumnos qué van a ser, refiriéndose a la carrera que cursan. Ellos responden que serán bioquímicos. Tras la respuesta, el maestro les da el siguiente ejemplo:

 

Extracto 5.35

P: Ahora fíjense cómo utiliza el físico esto. ¿Ustedes van a hacer qué?

As: ¡Bioquímicos!

P: Ustedes agarran este líquido... ¿Cómo le llaman?

As: (Risas).

P: Agarran un microbio y, por ejemplo, quieren saber cómo actúa y se reproduce a través de una sustancia ácida. Entonces, hacen el experimento y va cambiando tanto la sustancia como el color de ese microbio, observan cómo se reproduce, después lo tabulan y la gráfica resulta ser esta. Pero el que te dejó esta tarea o trabajo te dice: 'yo no quiero solamente la gráfica; quiero que tú me digas cuál es la función', porque si yo trabajo con la función la derivo, integro, maximizo o minimizo, le indico el punto de inflexión, su energía en tabulaciones. Entonces, yo quiero que le des la ecuación de la gráfica en pocas palabras; tú quieres saber a qué función se parece. Esa es tu tarea: ¿a qué función se parece? Entonces le aplicas una, dos, tres, cuatro, cinco, ¿qué vas a pensar? ¿Qué polinomio puede ser?

As: Cinco.

Este ejemplo consiste en "agarrar" un microbio y ver cómo "actúa" a través de una sustancia ácida, hacer el experimento y observar cómo van cambiando la sustancia y el color de dicho microbio, así como la manera en que se reproduce. Dicho fenómeno se puede constatar con una tabla de variación, ya que muestra la relación entre las dos cantidades. Se construye también la gráfica que relaciona las variables, aunque el docente indica lo que se quiere saber; en este caso, a qué función conocida se parece la gráfica obtenida y cuál es el grado del polinomio.

Aquí, el discurso surge cuando el profesor explica la relación que guarda el número de veces que una gráfica cruza al eje de las x's con relación al grado de la función polinomial respectiva. Intenta situarse en el contexto de los bioquímicos, pues pone como ejemplo al microbio.

 

DISCUSIÓN Y CONCLUSIONES

Se logró identificar una diversidad de perspectivas en las explicaciones de los profesores sobre la noción de función, al igual que sus ideas acerca de la variación, como la de parámetros –rota, traslada, la sube– o la asignación de un significado geométrico a las funciones (traslación, inclinación, rotación, desfasamiento, sube o baja, crece o decrece).

Además, los docentes le atribuyeron nociones de movimiento a las gráficas y a puntos de referencia como el vértice, el origen o la asíntota (dieron las expresiones se desplaza, sube o baja, se recorre, se mueve o corrimiento). También aproximaron valores a un número, df/dx a través de la variación de los valores del cociente o de un punto de referencia, así como la sucesión de puntos intermedios.

Consideramos que la estrategia de mover un punto de referencia (el vértice, el origen o la asíntota) fue de gran importancia para que los profesores construyeran sus explicaciones en torno al movimiento de la gráfica, apoyándose en una función básica, como f(x)=x, f(x)=x², f(x)=x³ o f(x)= sen x, entre otras. De ahí, enfatizaron el papel de la noción de variación.

Durante las clases registramos cinco tipos de explicación en las que pudo apreciarse la noción de variación:

• El modelo numérico

• El modelo de la representación geométrica

• El modelo algebraico

• El modelo de la comparación a/b

• El modelo del lenguaje natural

Estas fueron las representaciones o modelos que utilizaron los docentes para explicar los contenidos.

Dichas formas de explicar la noción de variación en aula se crean bajo el discurso construido tanto por el maestro como por sus alumnos, atendiendo a la especificidad del saber en juego, de acuerdo con la teoría de las situaciones didácticas, la cual destaca el hecho de que la situación de aprendizaje genere una serie de interacciones que hagan funcionales la comunicación y el intercambio de ideas. En tal sentido, los episodios que analizamos en el aula están estrechamente ligados con la búsqueda de una explicación satisfactoria para los actores de una interacción didáctica.

Resulta notorio que las situaciones de enseñanza analizadas se dan sobre la base de un conjunto de relaciones entre docente, alumnos y conocimiento, un supuesto básico de la teoría de las situaciones didácticas. Tales relaciones interesan a nuestro estudio porque son la base de las explicaciones portadoras de conocimiento; como hemos dicho anteriormente, el profesor explica al alumno con base en el millieu, ya que hace uso de cada uno de los elementos a su alcance en el momento dado (media naranja, jalar la onda, subir el vértice, entre otras expresiones). Esto es una característica notable en el fenómeno de envejecimiento, pues se acude a los recursos disponibles del maestro y de los alumnos al cambiar la explicación, que inevitablemente envejece a medida en que se usa.

Se producen modificaciones de las explicaciones con base en la interacción, propiciada por una búsqueda de complementariedad entre las versiones de los alumnos y la del maestro. Las intervenciones del profesor con la doble función de solicitar explicaciones y tratar de orientarlas regulan el curso de la clase. La situación de enseñanza cambia a través del empleo de explicaciones situadas.

La noción de variación, que es el centro de estudio en nuestra investigación, se apoya fuertemente en la de variación numérica, mientras que el modelo más socorrido fue el de la tabla de valores. Insistimos en que tales recursos no forman parte de lo que típicamente se considera el contenido matemático de una clase, sino con los que se amalgama la explicación en aula. La función no es la tabla, ni la fórmula, ni la gráfica; consiste en una relación de correspondencia específica. Su representación no la hace el concepto, pero a través de ellas el profesor lo hace aparecer en clase.

Respecto al fenómeno didáctico del envejecimiento de las situaciones de enseñanza, los profesores interactúan constantemente con los alumnos mediante el uso del saber explicado o bien de la explicación didáctica, en el sentido de Sierpinska. Esto ocurre con mayor intensidad cuando abordan la noción de variación, que no es objeto explícito de la enseñanza porque no es introducido al aula mediante una definición, ni es tratado en los libros de manera explícita, pues no se trata de una caracterización categorial. Su aparición ocurre junto con el lenguaje de uso, lo cotidiano que brinda el contexto, la variación de cosas relativas a la física, la ingeniería, etc.; ello es trasladado al juego de discursos formales y no formales. Tal hecho hace que el envejecimiento sea más rápido, ya que la cantidad de inciertos o eventualidades es mayor que cuando se introducen conceptos categoriales.

La generalización o sobre generalización, la analogía, la repetición sistemática, la reformulación y el cruce de lenguajes son los factores que, en nuestra consideración, más contribuyen al fenómeno de envejecimiento basado en las explicaciones.

Por ejemplo, cuando el profesor, como vimos en uno de los episodios, intenta generalizar al decir que dependiendo del grado del polinomio, [se sabrá cuántas] son las veces que cruzará el eje x, está haciendo una generalización incorrecta que ocasionará problemas al estudiante si la toma al pie de la letra, pues pronto encontrará contraejemplos. Esto exigirá que haya cambios en las explicaciones del profesor.

Nuestro estudio sobre el papel de la explicación en la clase de matemáticas intenta localizar, analizar y explicar cómo se desarrolla el fenómeno de envejecimiento de las situaciones de enseñanza. Los pasajes descritos muestran que el origen del cambio en la explicación del docente puede ser múltiple y muy complejo. Por ejemplo, el empleo de una generalización no válida, la repetición exhaustiva de un argumento o la combinación de leguajes inducen factores de cambio en el discurso del profesor y muy particularmente en sus explicaciones. Las raíces del envejecimiento se encuentran a nivel teórico.

Cuando el profesor demanda que los alumnos expongan su opinión, a través de preguntas motiva intervenciones explicativas, haciendo que resulte de sumo interés para los alumnos poder mover o desplazar el vértice de su posición inicial. El profesor intenta generalizar que, si a la función básica le suman una cantidad, la gráfica se desplaza hacia arriba; si le restan, hacia abajo.

 

BIBLIOGRAFÍA

Albert, J. A. (1996). La convergencia de series en el nivel superior. Una aproximación sistémica. Tesis de doctorado, Cinvestav, México.        [ Links ]

Artigue, M. (1991). Analysis. In D. Tall (De.). Advanced Mathematical Thinking (capítulo 11, pp.167–198). The Netherlands: Kluwer Academic Publishers, Mathematics Education Library.        [ Links ]

Ávila, R. (1996). Detección de algunos obstáculos que dificultan la asimilación y manejo de los conceptos presentes en el análisis y comprensión de los problemas sobre variación. Publicaciones Centroamericanas, 10 (1), 121–126.        [ Links ]

Ball, D. L. (1991). What's all this talk about discourse? Arithmetic Teacher, 39 (3), 44–48.        [ Links ]

Bartolini Bussi, M.G. (1998). Verbal interaction in the mathematics classrom: a vygotskian análisis. In H. Steinbring, M. G. Bartolini Bussi & A. Sierpinska (Eds.), Languaje and communication in the mathematics classrom (pp. 65–84). Reston, VA: NCTM.        [ Links ]

Brousseau, G. (1986). Fondaments et méthodes de la didactique des mathématiques. Recherches en Didactique des Mathématiques, 7 (2), 33–115.        [ Links ]

Candela, A. (1999). Ciencia en el aula. Los alumnos entre la argumentación y el consenso. México: Paidós.        [ Links ]

Candela, A. (1990). Investigación etnográfica en el aula: el razonamiento de los alumnos en una clase de ciencias naturales en la escuela primaria. Investigación en la Escuela, 11, 13–23.        [ Links ]

Cantoral, R. (1992). Acerca de la intuición del rigor: notas para una reflexión didáctica. Publicaciones Centroamericanas, 6 (1), 24–29.        [ Links ]

Cantoral, R. (1997). Pensamiento y lenguaje variacional. Documento interno, Cinvestav, IPN.        [ Links ]

Cazden, C. (1991). El discurso en el aula. México: Paidós.        [ Links ]

Chevallard, Y. (1991). La transposition didactique. Genoble, France: La Pensée Sauvage Éditions.        [ Links ]

Duval, R. (1999). Argumentar, demostrar, explicar: ¿continuidad o ruptura cognitiva? México: Grupo Editorial Iberoamérica (versión original en francés en Petit X31, 1992, 37–61).        [ Links ]

Edwards, D. y Mercer, N. (1987). El conocimiento compartido: el desarrollo de la comprensión en el aula. Barcelona, España: Paidós.        [ Links ]

Farfán, R. M. (1992). ¿Matemática educativa en el nivel superior? Seis años de investigación en la Reunión Centroamericana y del Caribe. Publicaciones Centroamericanas, 6 (2), 236–253.        [ Links ]

Flores, A., Sowder, J., Philipp, R. y Schappelle B. (1995). Orquestar, promover y mejorar el discurso matemático en el quinto grado: Estudio de un caso. Cuadernos de Investigación No. 32. México: Cinvestav–PNFAPM.        [ Links ]

García, M. (1998). Un estudio sobre la articulación del discurso matemático escolar y sus efectos en el aprendizaje del cálculo. Tesis de maestría, Cinvestav, México.        [ Links ]

Hoyos, V. (1996). La transición del pensamiento algebraico procedimental básico al pensamiento algebraico analítico. Tesis de doctorado, Cinvestav, México.        [ Links ]

Josse, E. y Robert, A. (1993). Introduction de I'homothetie en seconde, analyse de deux discours de professeurs. Recherche en Didactique des Mathématiques, 14 (2), 119–154.        [ Links ]

Mopondi, B. (1995). Les explications en classe de mathématiques. Recherches en Didactique des Mathématiques, 15 (3), 7–52.        [ Links ]

NCTM (2000). Principles and standars for School Mathematics. Reston, VA: NCTM.         [ Links ]

Piaget, J. (1973). La representación del mundo en el niño. Madrid, España: Morata.        [ Links ]

Pirie, S. (1988). Understanding: instrumental, relational, intuitive, constructed, formalised...? How can we know. For the Learning of Mathematics 8.        [ Links ]

Pimm, D. (1991). El lenguaje matemático en el aula. Madrid, España: Morata.        [ Links ]

Pimm, D. (1994). Mathematics classroom language: form, function and force. In R. Biehler, R. W. Schole, R. Strasser y B. Winkelmann (Eds.), Didactis of Mathematics as a Scientific Discipline (pp. 159–169). The Netherlands: Kluwer Academic Publishers.        [ Links ]

Pulido, R. (1998). Un estudio teórico de la articulación del saber matemático en el discurso escolar: la transposición didáctica del diferencial en la física y la matemática escolar. Tesis de doctorado, Cinvestav, México.        [ Links ]

Reséndiz, E. (2004). La variación en las explicaciones de los profesores en situación escolar. Tesis de doctorado, Cinvestav, México.        [ Links ]

Robinet, A. y Speer, N. (2001). Research on the teaching and learning of calculos/ elementary analysis. En D. Holton (Ed.), The Teaching and Learning of Mathematics at University Level. An ICMI Study (pp. 283–299). The Netherlands: Kluwer Academic Publishers.        [ Links ]

Robinson, A. (1996). Non–standard Analisis. Amsterdam, Holland: North Holland Publishing Company.        [ Links ]

Sierpinska, A. (1994). Understanding in Mathematics. London, England: The Falmer Press.        [ Links ]

Sfard, A. (2002). Learning mathematics as developing a discourse. In R. Speiser y C. Maher (Eds.), Proceedings of 21^st conference of PME–NA (pp. 23–44). USA, Columbus, Ohio: Clearing House for Science, Mathematics and Environmental Education.        [ Links ]

Seeger, F. (2001). Discourse and beyond: on the ethnography of classroom discourse. En H. Steinberg, M. Bartolini y A. Sierpinska (Eds.), Language and Communication in the Mathematics Classroom (pp. 85–101). National Council of Teachers of Mathematics.        [ Links ]

Tusón, A. y Unamuno, V. (1999). ¿De qué estamos hablando? El malentendido en el discurso escolar. Revista Iberoamericana de Discurso y Sociedad, 1, (1).        [ Links ]

Yackel, E. (2002). What we can learn from analysing the teacher's role in collective argumentaction. Journal of Mathematical Behavior, 21, 423–440.        [ Links ]

Zubieta, G. (1996). Sobre número y variación: antecedentes del cálculo. Tesis de doctorado, Cinvestav, México.        [ Links ]