Introducción
El transporte de fluidos en distintos procesos como en la industria del Gas, del petróleo, del agua, del riego agrícola y de pilas de lixiviación, entre otras, debe resolver la generación de fricción entre las paredes de las tuberías rugosas y el fluido en la trayectoria de flujos turbulentos, que provocan caídas de presión y en consecuencia requieren un gasto energético mayor para el transporte del fluido (Hernández et al., 2015). En el caso del gas, del petróleo y del agua, el transporte del fluido se realiza mediante tuberías con distintas rugosidades y con caudales variables de acuerdo con la demanda solicitada, donde el principal aspecto a revisar en el diseño de los distintos sistemas hidráulicos, corresponde a la presión de trabajo en las distintas secciones de una conducción. Lo mismo ocurre para el caso del riego agrícola y de pilas de lixiviación, donde las tuberías con salidas múltiples se utilizan en distintos sistemas de riego a presión, como la aspersión convencional, la aspersión de movimiento intermitente, la aspersión de movimiento continuo; la microirrigación y las tuberías multicompuerta para riego por gravedad. Para ambas situaciones es muy importante en la etapa de diseño de dichos sistemas, disponer de expresiones que permitan, con relativa facilidad, el cálculo de la pérdida de carga por fricción que se presenta en las tuberías que los constituyen y así, realizar una adecuada selección de las conducciones y equipos de impulsión necesarios para un correcto funcionamiento (Méndez & Riera, 2010). Es importante conocer de manera precisa el valor del factor de fricción para una adecuada estimación de las pérdidas de carga friccionales, así como posteriores presiones de trabajo en los diferentes puntos de un sistema hidráulico que se esté diseñando (Olivares et al., 2019).
Estas aplicaciones de la Mecánica de fluidos requieren el estudio de casos donde el Número de Reynolds, Re, y la rugosidad relativa de la tubería, ε/D, son las principales variables a considerar en su determinación. Esto ha motivado que a lo largo de la historia distintos autores estudian el fenómeno descrito y realizan aportes que resultan fundamentales como es el caso de Nikuradse J., Moody L. F. y Colebrook C. F., entre otros.
Como el resultado más relevante del trabajo de Colebrook, en 1939 surge la ecuación para determinar el factor de fricción (f) en tuberías para flujos en transición y turbulentos como se presenta en la ecuación (1) (Colebrook, 1939):
Donde:
f = factor de fricción
Re = Número de Reynolds
ε/D = rugosidad relativa de la tubería
Se puede observar claramente que la ecuación (1) es una expresión implícita que requiere una solución numérica aproximada (Olivares et al., 2019) o una solución de tipo analítica exacta para estimar el factor de fricción (Mikata &Walczak, 2017).
Muchos autores han propuesto aproximaciones de la ecuación de Colebrook basada en regresiones o ajustes de los valores proporcionados por dicha ecuación, que permiten una determinación del factor de fricción con amplios rangos de precisión en la solución asociada a los valores de Re y ε/D utilizados. Estas correlaciones son de carácter explícitas y permiten una rápida determinación de valores aproximados (Olivares et al., 2019; Anaya et al., 2014; Winning & Coole, 2013).
En el caso de la forma implícita original de la ecuación de Colebrook, se requiere el uso de métodos numéricos para la búsqueda de su solución, lo que permite la determinación de valores aproximados que tienen una precisión que es elegida por el usuario y depende de los recursos computacionales disponibles y de los tiempos de procesamiento.
Varios son los autores que han desarrollado diferentes técnicas iterativas con el objetivo de aproximar una solución de la ecuación de forma f(x)=0. Entre estos esfuerzos está el método iterativo más estudiado y empleado para la aproximación de raíces para resolver ecuaciones como la de Colebrook, que es el método de Newton (Ypma, 1995). El método tiene convergencia de segundo orden en el entorno de una raíz simple bajo ciertas condiciones. Además, una de las características más interesantes del método de Newton es su equilibrio entre el costo operacional y la velocidad de convergencia (Kocak, 2011).
Bajo condiciones apropiadas de la función f(x) y de la elección del valor inicial x0, el método de Newton genera una secuencia {xn} de valores, que converge a una solución x* para la ecuación f(x)=0. Por lo tanto, se cumple que lim n→∞ xn = x*, el número x* es punto fijo, es decir, h(x*) = x*. El punto fijo x* de la función de iteración h es una raíz de la función f(x).
El método de Newton tiene una interpretación geométrica sencilla, que en realidad está en el origen histórico del mismo. En efecto, en cada etapa k, el valor xn+1 corresponde a la abscisa del punto de intersección con el eje x de la recta tangente a la curva y = f(x) en el punto (xn, f(xn)) y sugiere este valor como la próxima aproximación a x*. Esta interpretación geométrica justifica que este método reciba también el nombre de método de la tangente.
Existen muchos otros métodos iterativos para aproximar la solución de ecuaciones no lineales como es el caso de la ecuación de Colebrook. Algunos de ellos son variantes del método de Newton, que buscan una reducción del costo computacional o aumentar la velocidad de convergencia introduciendo factores o coeficientes que aceleran el proceso. En este grupo está el método de Chebyshev, Halley y Ostrowski, que son los más conocidos.
Todos estos métodos corresponden a los métodos iterativos clásicos que derivan del método de convergencia de segundo orden de Newton. El método de Halley es un método de tercer orden de convergencia y es uno de los más redescubiertos en la literatura matemática (Gander, 1985). Otro método iterativo de tercer orden que frecuentemente se utiliza en la resolución de ecuaciones no lineales es el método de Chebyshev. Este método posee en la literatura matemática varias formas para nombrarlo, pero la de Chebyshev es la más recurrente (Grau & Díaz, 2006a). El método iterativo de Ostrowski es otro método de solución numérica que posee un cuarto orden de convergencia. Este método ha sido poco utilizado en la resolución de ecuaciones no lineales, pero en la literatura se encuentran importantes aportes tendientes a mejorar su orden de convergencia y disminuir los tiempos computacionales de los procesos de resolución (Grau & Díaz, 2006b).
Sin embargo, en la actualidad son muchos los métodos iterativos disponibles que se han aplicado para la resolución de la ecuación implícita de Colebrook como son los métodos: Sharma et al. (2013); Sharma & Sharma (2010); Sharma & Arora (2016); Džunić et al. (2011 y 2012); Bi et al. (2009); Chun & Neta (2012) basado en Kung & Traub (1974), Neta & Jhonson (2008), el método Jain (2007) basado en el esquema de Steffensen (Khattri & Agarwal, 2010; Cordero et al., 2014; 2012; Soleymani & Vanani, 2011), entre otros métodos (Praks & Brkić, 2018).
Mikata & Walczak en 2015 propusieron una solución analítica exacta basada en la recursividad infinita para la ecuación de Colebrook, llamada fórmula n-ésima. Esta solución se basa en el empleo de la forma cerrada de la expresión para una función asociada a la función W de Lambert, llamada función Y. Esta función Y se expresa por una recursión infinita que permite observar que el error absoluto disminuye geométricamente hacia cero dependiendo de la profundidad de la recursión (Mikata & Walczak, 2015; Alfaro et al., 2019). En 2017, Mikata & Walczak plantearon que existen tres tipos de soluciones para la ecuación de Colebrook clasificándolas como de primera, segunda y tercera generación (Mikata & Walczak, 2017).
Las soluciones de primera generación corresponden a las aproximaciones basadas en ajustes de curvas con datos obtenidos de la ecuación de Colebrook, como son las correlaciones propuestas por Manadilli & Silverberg, 1997; Buzzelli (2008); Brkić (2011a y 2011b); Romeo et al. (2002); Fang et al. (2011), Haaland (1983), entre otras.
Las soluciones de segunda generación corresponden a aproximaciones basadas en la función W de Lambert utilizadas para resolver la ecuación de Colebrook, como la de Boyd (1998); Barry et al. (2000) y Winitzki (2003). Brkić (2012) comparó los resultados de la W de Lambert para encontrar correlaciones explicitas que permiten el cálculo del factor de fricción, encontrando que algunas correlaciones son más apropiadas que otras desde el punto de vista computacional debido a que algunas requieren la evaluación de términos con valores numéricos fuera de los rangos de la mayoría de las computadoras, además de que no se pueden aplicar para ciertos valores de rugosidad relativa y números de Reynolds. Pero otras correlaciones no presentan estas limitaciones y permiten obtener buenos resultados (Brkić, 2012).
Por último, las soluciones de tercera generación son las aproximaciones basadas en soluciones analíticas exactas de la ecuación de Colebrook. La fórmula n-ésima pertenece a las soluciones de tercera generación y permite facilidad de uso y precisión en los resultados (Alfaro et al., 2019). Esta solución, propuesta por Mikata & Walczak, utiliza los mismos coeficientes de la ecuación de Colebrook, consiguiendo mejor precisión al aumentar la profundidad de recursión “n” (Mikata & Walczak, 2015).
La fórmula n-ésima requiere un proceso recursivo para su solución y, por ello, la generación de un algoritmo para evaluar su profundidad. La recursión y la iteración son técnicas de programación que suelen utilizarse en programas computacionales para resolver rápidamente problemas complejos y repetitivos. Un programa recursivo simplifica un problema y lo resuelve de abajo hacia arriba. Estos algoritmos recursivos contienen llamados a sí mismos de forma finita y se utilizan mayormente en problemas relacionados con las áreas matemáticas, fundamentalmente cuando el problema se define en términos de sí mismo. Cabe resaltar que la recursividad es una forma elegante, simple, estructurada, modular y clara de resolver problemas complejos en pocas líneas de código, por lo tanto, resulta de gran utilidad (Murillo & Caamaño, 2013).
Un proceso iterativo se repite una y otra vez (iteraciones) empezando cada nueva iteración con el resultado de la iteración anterior. Es decir, cada paso origina el paso siguiente y el proceso continúa hasta que se alcanza una meta determinada y el proceso termina (Sharifi et al., 2015).
La diferencia más importante entre las operaciones recursivas y las iterativas es que los pasos de una operación iterativa se realizan uno cada vez y dirigen la ejecución directamente al siguiente paso. En una operación recursiva, cada paso después del paso inicial es una réplica del paso anterior. Además, desde arriba hacia abajo, cada paso es un poco más sencillo que el que hay justo "encima". Al final de la operación, todas las soluciones se combinan para resolver el problema.
El objetivo del presente trabajo es estudiar el efecto de la profundidad de recursión “n” para determinar el factor de fricción para la ecuación de Colebrook, utilizando la solución analítica exacta de Mikata & Walczak (2015).
Materiales y métodos
Solución analítica de la ecuación de Coolebrok
Mikata & Walczak (2015), plantean dos soluciones analíticas exactas de la ecuación de Colebrook, una por recursión infinita y la otra mediante una integral. Estas soluciones son las primeras soluciones analíticas exactas que no usan la función W de Lambert y utilizan la función Y generando una forma cerrada por recursión infinita (Mikata & Walczak, 2015).
La ecuación (1) se puede reordenar con base en nuevas constantes y luego aplicar la función W de Lambert definida en la ecuación (2).
Luego si se introduce otra función llamada función Y, como se muestra en ecuación (3).
Esta función Y es exactamente la misma función que la función ω definida por Clamond (2009) y también por Lawrence et al. (2012), donde la función se llama función Wright ω.
Luego de introducir estas funciones y constantes, se obtiene lo siguiente:
Donde:
La ecuación (5) es una solución exacta de forma cerrada de la ecuación de Colebrook en términos de la función Y. Donde c 1 , x 0 y x 1 se definen en las ecuaciones (6), (7) y (8), además Y(x) está dado por la ecuación (9), (Mikata & Walczak, 2015).
Usando las ecuaciones (5) y (9) para un x 1 mucho mayor que 1, para rangos prácticos de Re y ε/D como los del diagrama de Moody (1944), se obtiene la solución de la ecuación de Colebrook en las ecuaciones (10), (11), (12) y (13).
Donde, f n es la n-ésima aproximación para el valor exacto de f, que corresponde al factor de fricción de Colebrook exacto. Esta solución puede ser truncada para un valor de n finito, el que definirá el nivel de precisión de la solución final (Mikata & Walczak, 2017).
La ecuación (13) tiene una estructura típicamente recursiva debido a que el cálculo que se debe realizar en cada paso es una réplica del cálculo realizado en el paso anterior, lo que permite generar un algoritmo recursivo de resolución. Este proceso recursivo de cálculo genera una gran cantidad de operaciones y un gran número de datos para cada nivel de profundidad de recursión. Es por ello que se ha desarrollado un programa en lenguaje Excel-VBA que permite resolver de manera masiva los valores del factor de fricción para tuberías rugosas considerando los rangos de valores de Re y ε /D que se detallan en adelante.
En este análisis se ha determinado cada uno de los valores del factor de fricción y luego el porcentaje máximo de error relativo considerando valores de ε/D entre 10-1 y 10-6 y valores de Re entre 104 y 108, lo que genera una matriz de análisis para el factor de fricción que contiene 839.937 valores.
En la Figura 1 se muestra la distribución de valores en la hoja de cálculo de Excel, los que son leídos directamente por la Macro de Excel para no generar errores por ingreso manual de datos o por pantalla. En primer lugar, se debe ubicar en la celda A1 el valor de la profundidad de recursión (n) que se requiere calcular en cada planilla. También se deben rellenar los valores de ε/D, los que se deben ubicar en la hoja de cálculo de Excel en la fila 1 entre la celda B1 (ε /D=10-1) y la celda V1 (ε /D=10-6).
Se pueden visualizar los valores de Reynolds en la Figura 1, los que deben ser ubicados en la columna A entre la celda A2 (Re=104) y la celda A39998 (Re=108) en intervalos de 2,500 unidades para cada valor de Re, llegando a considerar un total de 39.997 valores.
La Macro desarrollada en lenguaje Excel-VBA se denominó “Profund_Recurs” y su código de programación se presenta en la Figura 2.
Una vez cargada la Macro en la pestaña “vista” posteriormente se aplica “ejecutar” para rellenar la hoja de cálculo. Este paso demorará varios minutos debido al procesamiento de la gran cantidad de datos. Utilizando la Macro de Excel-VBA se han calculado los factores de fricción para valores de profundidad de recursión n=1 a n=10 y adicionalmente para n=20 como valores base de comparación.
Parámetros estadísticos
Los parámetros estadísticos utilizados para evaluar los errores en la predicción del factor de fricción asociado a las diferentes profundidades de recursión, corresponden a parámetros de estadística descriptiva (Vivanco, 2005). En una medida directa o indirecta de un equipo utilizando una fórmula como en este caso, debe existir un tratamiento de datos, el cual permita distinguir los dos tipos de errores más utilizados (Dolores et al., 2012). Estos errores corresponden al error absoluto de la diferencia entre el valor de la medida y el valor tomado como exacto, pudiendo ser positivo o negativo, según si la medida es superior o inferior al valor real. El otro descriptor es el error relativo, el cual corresponde al cociente entre el error absoluto y el valor exacto, también pudiendo ser su valor positivo o negativo (Ercilla & Muñoz, 2003).
La determinación de algunos parámetros estadísticos permitirá establecer la calidad de la aproximación de los resultados para el factor de fricción en las distintas profundidades de recursión (Shaikh et al., 2015).
Si se considera que [f estimado ] es la matriz de valores para el factor de fricción en cada uno de los niveles de recursión analizados y que [f CW ] es la matriz de valores del factor de fricción de Colebrook resultantes de la solución de la ecuación (1) para una profundidad de recursión n=20 en cada nodo de la matriz de valores de Re y ε /D, entonces es posible definir los siguientes parámetros estadísticos:
Máximo Error relativo positivo (%)
Se puede obtener el porcentaje máximo de error relativo positivo para cada correlación que aproxima el valor del factor de fricción de Colebrook. Este parámetro se define por la ecuación (14).
Máximo Error relativo negativo (%)
Para obtener el porcentaje máximo del error relativo negativo para cada correlación que aproxima el valor del factor de fricción de Colebrook, se debe aplicar la ecuación (15).
Error relativo promedio (%)
Si N es el número total de elementos de la matriz de análisis del factor de fricción para los distintos valores de ε/D y Re, se puede obtener el valor del error relativo promedio en porcentaje, utilizando la ecuación (16):
Resultados y discusión
Error asociado a cada profundidad de recursión (Sub-sección)
Para no realizar un cálculo con una profundidad de recursión infinita como lo plantea la solución analítica exacta de Mikata & Walczak (2015), se ha considerado como una buena aproximación de la solución de la ecuación de Colebrook, el resultado para una profundidad de recursión n=20. Este nivel de recursión permite determinar el factor de fricción con una precisión e invariabilidad de 15 cifras decimales.
Estos valores del factor de fricción (n=20) han sido tomados como base de comparación con los distintos resultados obtenidos para valores de Re entre 104 y 108 y valores de ε/D entre 10-1 y 10-6 y para una profundidad de recursión que va desde n=1 a n=10.
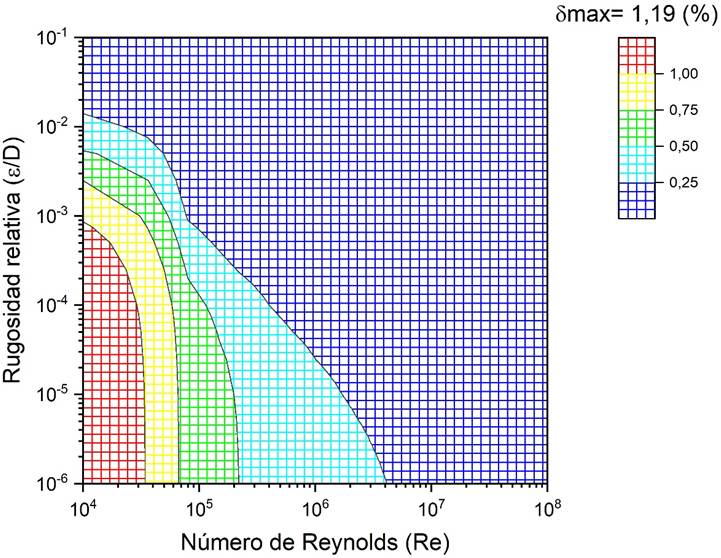
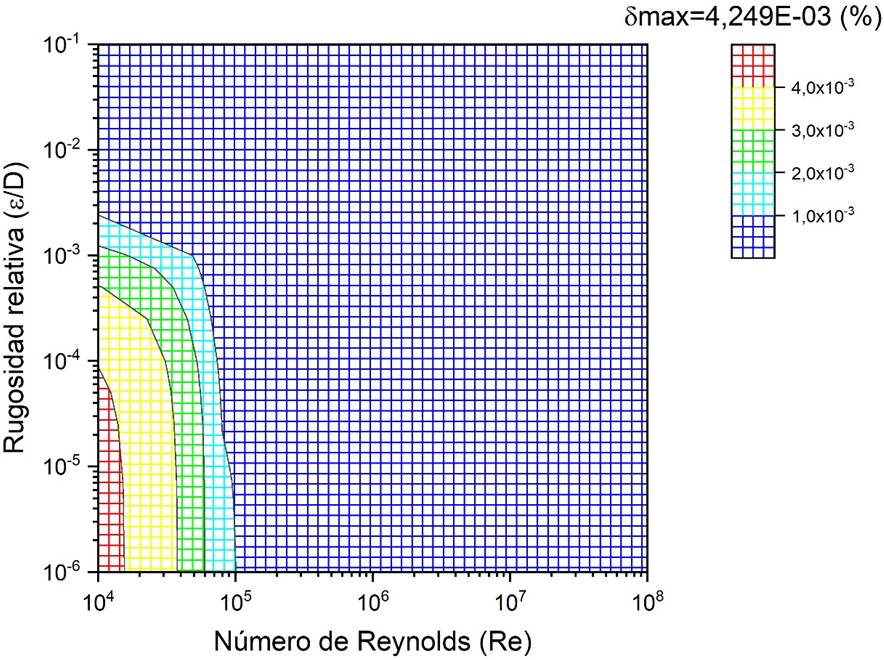
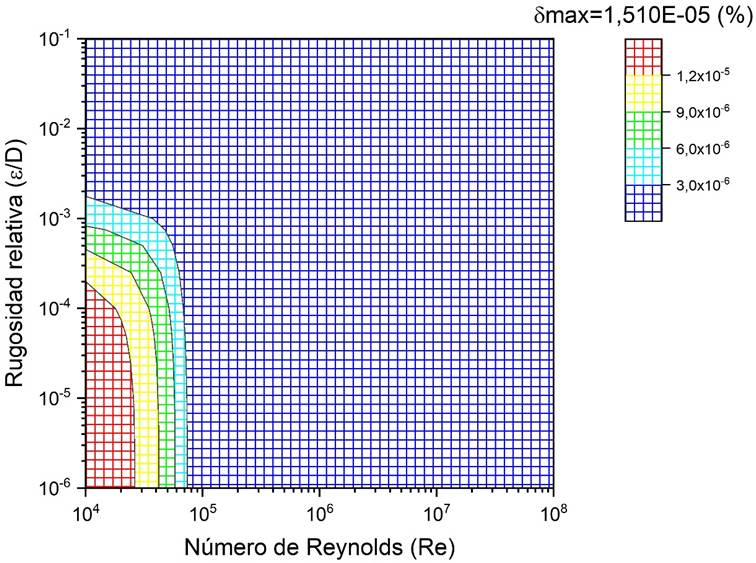
En las Figuras 3 a la 12 se grafican los resultados para el error relativo porcentual, donde es posible apreciar la rápida reducción de dicho error al aumentar la profundidad de recursión.
Para valores de n=1 se obtiene un error relativo porcentual máximo de 1.188 %, que se puede apreciar como disminuye a medida que aumenta la profundidad de recursión y se llega a obtener un error relativo porcentual máximo de 5.369E-08 % para n=10.
Estos errores relativos porcentuales muestran un comportamiento alternado en su signo generando un amortiguamiento en torno al error cero. De igual forma, es posible establecer que el error relativo promedio decrece de manera sostenida demostrando una disminución rápida del error de los N elementos que son considerados en el análisis. En la Tabla 1 se muestran los valores de los máximos errores relativos porcentuales tanto positivos como negativos y sus promedios.
Tabla 1: Máximos errores relativos porcentuales positivos y negativos
| n | MAX ER + | MAX ER - | ER Prom |
|---|---|---|---|
| 1 | 1.188E+00 | 5.056E-10 | 1.772E-02 |
| 2 | 0.000E+00 | 1.826E-01 | 9.488E-04 |
| 3 | 2.784E-02 | 0.000E+00 | 6.183E-05 |
| 4 | 0.000E+00 | 4.249E-03 | 4.632E-06 |
| 5 | 6.485E-04 | 0.000E+00 | 3.883E-07 |
| 6 | 0.000E+00 | 9.897E-05 | 3.582E-08 |
| 7 | 1.510E-05 | 0.000E+00 | 3.586E-09 |
| 8 | 0.000E+00 | 2.305E-06 | 3.849E-10 |
| 9 | 3.518E-07 | 0.000E+00 | 4.377E-11 |
| 10 | 0.000E+00 | 5.369E-08 | 5.221E-12 |
En la Figura 13 se presenta un resumen del máximo error relativo porcentual en función de la profundidad de recursión n, donde es posible apreciar el rango de error que se adopta en la estimación del factor de fricción de Colebrook y así de forma rápida se puede evaluar la precisión de la solución implementada en futuros cálculos de sistemas de distribución reales.
Ejemplo de aplicación
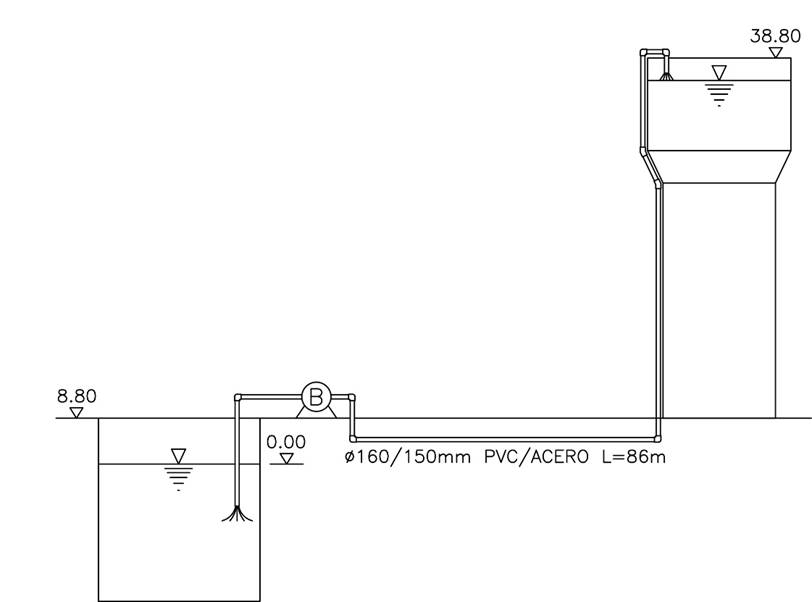
Se desea trasladar agua de un pozo a un estanque elevado con una bomba centrífuga de acuerdo como se presenta en la Figura 14. Para ello, es necesario determinar la potencia requerida de la bomba a instalar, si se sabe que debemos trasladar un caudal entre los 3 y 4 L/s, se utilizará en primer lugar una tubería de acero de diámetro 150 mm, y luego como alternativa una tubería de PVC PN-10 de diámetro 160 mm.
La potencia de una bomba se determina como lo muestra la ecuación (17):
Donde:
γ = peso específico del agua
Qb = caudal de la bomba
Hb = altura de la bomba
A continuación, se presenta la ecuación (18) que permite el cálculo de Hb:
Donde:
Δz = diferencia geométrica de altura del agua entre los puntos que se debe trasladar
ΔHf = pérdida de carga total del sistema despreciando las pérdidas singulares.
A continuación, se presenta la ecuación (19) que permite el cálculo de ΔHf:
Donde:
L = longitud de la conducción
V = velocidad de escurrimiento de agua en la tubería
D = diámetro interior de la conducción
f = factor de fricción
Para determinar el valor de f se utilizará la Macro desarrollada en Excel VBA “Profund_Recurs”, y se determinará posteriormente lo indicado en el enunciado del problema para los casos presentados en la Tabla 2, donde además se presentan los valores de la rugosidad de la conducción (ε, rugosidad relativa (ε/D), velocidad de escurrimiento (Vesc) y el número de Reynolds (Re).
Tabla 2: Presentación de variables según caso de aplicación
| Caso | Material | D (mm) | ε (mm) | ε /D | Caudal (L/s) | Velocidad (m/s) | Re |
|---|---|---|---|---|---|---|---|
| I | Acero | 150.0 | 0.1500 | 0.0010000 | 3.00 | 0.170 | 25288 |
| II | Acero | 150.0 | 0.1500 | 0.0010000 | 4.00 | 0.226 | 33717 |
| III | PVC | 144.6 | 0.0015 | 0.0000104 | 3.00 | 0.183 | 26232 |
| IV | PVC | 144.6 | 0.0015 | 0.0000104 | 4.00 | 0.244 | 34976 |
Los valores presentados en la Tabla 2 se utilizan para determinar f con la Macro Excel VBA, donde además se presenta el valor exacto de f, cuyos resultados se muestran en la Tabla 3.
Tabla 3: Valores de f según caso de aplicación y profundidad de recursión
| Caso | Profundidad de recursión | f | % Error relativo | Valor exacto de f |
|---|---|---|---|---|
| I | 1 | 0.02659817435518350 | 0.5770141 | 0.0267525402847864 |
| 2 | 0.02676777042557680 | 0.056929699 | ||
| 3 | 0.02675104384010820 | 0.005593655 | ||
| 4 | 0.02675268737848800 | 0.000549831 | ||
| 5 | 0.02675252582672300 | 5.40437E-05 | ||
| 6 | 0.02675254170589700 | 5.31206E-06 | ||
| 7 | 0.02675254014510270 | 5.22132E-07 | ||
| 8 | 0.02675254029851610 | 5.13213E-08 | ||
| 9 | 0.02675254028343680 | 5.04449E-09 | ||
| 10 | 0.02675254028491900 | 4.95844E-10 | ||
| II | 1 | 0.02535345939625800 | 0.473381915 | 0.0254740489370163 |
| 2 | 0.02548466636437770 | 0.041679387 | ||
| 3 | 0.02547311728157400 | 0.003657273 | ||
| 4 | 0.02547413071206250 | 0.000321013 | ||
| 5 | 0.02547404175948810 | 2.81758E-05 | ||
| 6 | 0.02547404956700100 | 2.47305E-06 | ||
| 7 | 0.02547404888172140 | 2.17064E-07 | ||
| 8 | 0.02547404894186960 | 1.90521E-08 | ||
| 9 | 0.02547404893659030 | 1.67223E-09 | ||
| 10 | 0.02547404893705370 | 1.46764E-10 | ||
| III | 1 | 0.02405349170386600 | 0.879762957 | 0.0242669836367188 |
| 2 | 0.02429589246066130 | 0.119128213 | ||
| 3 | 0.02426309266202460 | 0.016034027 | ||
| 4 | 0.02426750776753730 | 0.002159852 | ||
| 5 | 0.02426691304180620 | 0.000290909 | ||
| 6 | 0.02426699314525190 | 3.9183E-05 | ||
| 7 | 0.02426698235600300 | 5.27761E-06 | ||
| 8 | 0.02426698380922000 | 7.10847E-07 | ||
| 9 | 0.02426698361348440 | 9.57449E-08 | ||
| 10 | 0.02426698363984820 | 1.2896E-08 | ||
| IV | 1 | 0.02250523601401800 | 0.808420164 | 0.0226886556815408 |
| 2 | 0.02271262857497550 | 0.105660264 | ||
| 3 | 0.02268553959361840 | 0.013734123 | ||
| 4 | 0.02268906101217700 | 0.00178649 | ||
| 5 | 0.02268860296234480 | 0.000232359 | ||
| 6 | 0.02268866253852870 | 3.02221E-05 | ||
| 7 | 0.02268865478967960 | 3.93087E-06 | ||
| 8 | 0.02268865579754170 | 5.11273E-07 | ||
| 9 | 0.02268865566645300 | 6.64992E-08 | ||
| 10 | 0.02268865568350320 | 8.64928E-09 |
Finalmente, en la Tabla 4, para cada caso según valor de f obtenido, reemplazamos sucesivamente las ecuaciones (17), (18) y (19) para obtener la potencia requerida de la bomba a instalar.
Tabla 4: Resultados obtenidos para determinar la potencia de la bomba
| Caso | ΔHf (m) | Δz (m) | Hb (m) | Potencia (Watt) |
|---|---|---|---|---|
| I | 0.0224004 | 38.80 | 38.82240 | 1142.5432 |
| 0.0225432 | 38.80 | 38.82254 | 1142.5474 | |
| 0.0225291 | 38.80 | 38.82253 | 1142.5470 | |
| 0.0225305 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| 0.0225304 | 38.80 | 38.82253 | 1142.5471 | |
| II | 0.0379593 | 38.80 | 38.83796 | 1143.0011 |
| 0.0381558 | 38.80 | 38.83816 | 1143.0069 | |
| 0.0381385 | 38.80 | 38.83814 | 1143.0064 | |
| 0.0381400 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| 0.0381399 | 38.80 | 38.83814 | 1143.0065 | |
| III | 0.0243331 | 38.80 | 38.82433 | 1142.6001 |
| 0.0245783 | 38.80 | 38.82458 | 1142.6073 | |
| 0.0245451 | 38.80 | 38.82455 | 1142.6064 | |
| 0.0245496 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| 0.0245490 | 38.80 | 38.82455 | 1142.6065 | |
| IV | 0.0404743 | 38.80 | 38.84047 | 1143.0752 |
| 0.0408473 | 38.80 | 38.84085 | 1143.0861 | |
| 0.0407986 | 38.80 | 38.84080 | 1143.0847 | |
| 0.0408049 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408041 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408042 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408042 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408042 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408042 | 38.80 | 38.84080 | 1143.0849 | |
| 0.0408042 | 38.80 | 38.84080 | 1143.0849 |
Si revisamos los resultados obtenidos para la potencia de la bomba, en cada uno de los casos de estudio se puede apreciar que estamos cerca de la solución exacta cuando la profundidad de la recursión es n=3. En las Figuras 15, 16, 17 y 18 se puede apreciar lo comentado para cada caso.
Conclusiones
En este artículo se presentan los resultados para distintas profundidades de recursión comprobando que para un valor n=20 se tiene una solución para la ecuación implícita de Colebrook con una adecuada precisión. El error relativo porcentual positivo o negativo junto al error relativo promedio tienen un comportamiento decreciente con rápida convergencia hacia el error cero. La precisión de la solución depende de la profundidad de recursión llegando a valores de 5.369E-08 % para n=10. La simplicidad de la estructura de la fórmula n-ésima facilita el proceso recursivo de determinación del valor del factor de fricción generando un ahorro en el tiempo computacional y cantidad de operaciones. Lo anterior se demuestra en los resultados obtenidos para el ejemplo de aplicación presentado, donde los resultados se acercan a la solución esperada en cada caso resuelto a partir de n=3.











 nueva página del texto (beta)
nueva página del texto (beta)