Introducción
En 1994 el temblor de Northridge, California generó inesperadas fallas frágiles en conexiones soldadas de acero y desató un proceso de cuestionamiento y revisión de los estándares y prácticas en el diseño de conexiones de acero ante condiciones sísmicas (Trembley et al., 1996; Bruneau et al., 1998). Este acontecimiento renovó el interés de los investigadores en revisar las hipótesis y generalizaciones que, en la práctica, subyacen en la selección de determinados tipos de conexiones y se publicaron estudios analíticos y experimentales tendientes a dar guías y a recomendar ciertos tipos de conexiones.
Una de las propuestas más estudiadas fue la placa de extremo, en particular, en 1994 se analizaron placas de extremo con comportamiento bilineal y endurecimiento por deformación, así como tornillos con comportamiento trilineal (Bahaari & Sherbourne, 1994). En otras propuestas, se realizaron modificaciones a tipos de conexiones recomendadas antes del temblor de Northridge, como la adición de placas niveladoras (Meng & Murray, 1995). En otra línea de investigación, buscando darle mayor flexibilidad a la conexión, en vez de propiciar grandes esfuerzos, se analizaron con mayor detalle modelos en 3D de tornillos sin placa extremo y considerando deformaciones excesivas (Choi & Chung, 1996). Hasta aquí, ya se sospechaba de un mejor comportamiento por parte de las conexiones semi-rígidas.
Tratando de caracterizar la capacidad de absorción de energía inelástica, se generaron curvas momento-rotación para conexiones de placa de extremo (Bursi & Jaspart, 1998). También, se evaluó la ductilidad y disipación de energía de 22 especímenes de secciones “T” (Nemati et al., 2000).
Explorando la causa de las fallas sucedidas en Northridge, se estudió la fractura frágil de filetes de soldadura bajo un número pequeño de ciclos de carga (Bursi et al., 2002). También, se extendieron los estudios a los análisis paramétricos de curvas momento-rotación para conexiones semi-rígidas, con placa de extremo para varias rigideces iniciales, varias rigideces de endurecimiento por deformación y varios factores de forma (Kishi et al., 2004).
La conexión entre el alma de la columna y una placa atiesadora también fue evaluada para comparar la diferencia entre una conexión rigidizada y una no rigidizada (Guo et al., 2006) y, en cuanto al desarrollo de análisis de vulnerabilidad para estructuras de acero, se propusieron curvas de vulnerabilidad para el marco crítico de edificios con excitaciones registradas en Northridge (Li & Ellingwood, 2008). En el presente estudio se adapta este análisis de vulnerabilidad para obtener la probabilidad de falla de la conexión bajo aceleraciones sísmicas de diseño recomendadas para la Ciudad de México.
Entre los estudios de laboratorio, se han analizado combinaciones de placas de extremo con 8 tornillos y se han comparado los resultados del comportamiento con estudios analíticos considerando propiedades 3D elastoplásticas, sin endurecimiento por deformación para columnas, vigas y placas de extremo donde el sismo se ha simulado como una carga monotónica (Shi et al., 2006).
Diversas agencias en los Estados Unidos han propuesto conexiones precalificadas, con el ánimo de proporcionar guías básicas para estructuras de acero construidas en los Estados Unidos (AISC, 2010; FEMA, 2000; NEHRP, 2009). Sin embargo, esto no garantiza un comportamiento adecuado ante otros tipos de temblores como los que se presentan en la Ciudad de México, que producen altas amplificaciones de desplazamientos y un alto número de ciclos de disipación de energía, por lo que este trabajo pretende aportar en esta dirección.
Se utilizarán también, resultados de trabajos previos para introducir las incertidumbres en cargas y resistencias y para plantear la esperanza del costo en el ciclo de vida (Ang & De León, 2005; De León, 2007; Aguirre & Carvajal, 2010) incluyendo la estimación explícita de consecuencias de falla como, por ejemplo, el costo asociado a fatalidades el cual, más que asignar un valor a la vida humana, sigue la aproximación del capital humano, que calcula la pérdida que sufre la sociedad al dejar de aportar a la misma los ingresos que hubiese obtenido de no fallecer en el colapso del edificio y haber trabajado hasta el momento de su retiro laboral.
La incertidumbre en las respuestas mecánicas derivadas de la demanda sísmica, usualmente medida a través del coeficiente de variación, así como las correspondientes a las capacidades respectivas, se toman de trabajos previos (Rosenblueth, 1986; Hancock, 2001). Las cargas muerta y viva se consideran deterministas.
Para establecer las alternativas de tipos de conexiones y los estados límite asociados a los mismos, se toma como base lo planteado en una investigación previa (De Leon et al., 2013).
El presente trabajo se basa en una tesis de maestría desarrollada previamente (Trueba, 2017).
Método propuesto
Descripción general
La metodología propuesta se basa en un proceso simplificado de simulación de Monte Carlo que incluye, principalmente:
Modelación probabilística de la excitación sísmica por medio del uso de espectros de aceleración recomendados en normas mexicanas para el sitio.
Cálculo de la respuesta máxima de la estructura para aceleraciones prescritas, para generar una función que relacione la respuesta máxima con la aceleración prescrita.
Simulación de Monte Carlo para obtener ensayos de aceleraciones, con distribución lognormal (LN), y respuestas máximas usando la función encontrada en el paso 2.
Simulación de Monte Carlo para obtener ensayos de capacidades, con distribución lognormal (LN).
Cálculo de probabilidades de falla condicional e incondicional a la ocurrencia del sismo.
Cálculo de costos esperados en el ciclo de vida.
De manera esquemática, la Figura 1 muestra los pasos 3 al 6. Los pasos 1 y 2 son generales, válidos para las 3 conexiones, mientras que los pasos 3 al 6 se repiten para cada conexión.
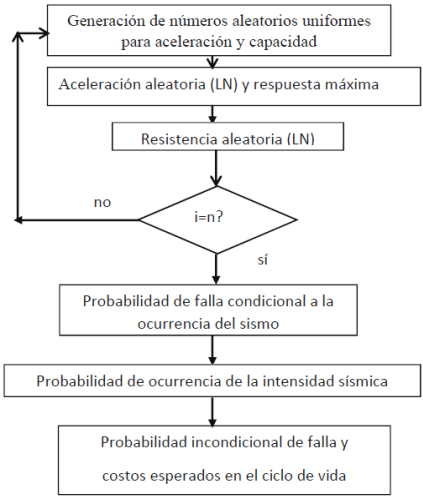
Figura 1: Representación esquemática del procedimiento para cada tipo de conexión, para los pasos 3 a 6
La formulación analítica se plantea en la próxima sección y los valores específicos de los parámetros mecánicos (geometría y propiedades mecánicas de los materiales del edificio) y costos correspondientes al edificio y las pérdidas consideradas dentro de las consecuencias de falla, se presentan y discuten en la siguiente sección.
Fundamento analítico
La probabilidad de falla de la conexión, base para el cálculo de la probabilidad de falla del edificio, se expresa en términos del efecto mecánico de la carga (que incluye carga muerta, viva y de sismo) C y la resistencia o capacidad R:
Se supone como condición de colapso del edificio la falla de tres niveles del mismo en las conexiones de ambos extremos de la misma bahía. Esto, con el fin de asociar la falla del edificio con una condición de daño extensivo, que provocaría la perturbación de la operación de las actividades del mismo de manera significativa. Así, la probabilidad de falla del edificio quedaría definida como se observa en la Ecuación (2):
Para obtener los elementos mecánicos máximos C en la conexión, primero deben obtenerse conforme se describió en la metodología, las respuestas máximas en la junta crítica, bajo la combinación de cargas que producen los resultados más desfavorables en el edificio.
Los datos de geometría del edificio, secciones de los miembros, propiedades mecánicas del acero, cargas vivas, espectro de aceleraciones y costos se detallan más adelante.
Las incertidumbres en cargas C y resistencias R se modelan de la siguiente manera:
La aceleración espectral correspondiente a la zona central del espectro recomendado por las Normas de Diseño sísmico en la Ciudad de México, el cual se describe en el siguiente apartado, se toma como lognormal. Si la masa es constante, la fuerza sísmica será también lognormal. Por ejemplo, para el escenario con intensidad sísmica a = 0.4 g:
De acuerdo con una investigación previa (Nemati et al., 2000):
Es conocido que:
Y los parámetros de la distribución lognormal:
Una vez que se tienen los parámetros de la distribución lognormal, los ensayos para la aceleración sísmica aleatoria, con distribución lognormal, se obtienen generando números con distribución uniforme y luego aplicando la Ecuación (8):
Las resistencias se simulan también con distribución lognormal, considerando CVR = 0.1 NERHP (2009) y aplicando:
Las medias de las resistencias se obtienen de las capacidades nominales de tornillos o soldadura, de acuerdo con el tipo de conexión considerado y al estado límite que rija.
Finalmente, aplicando técnicas de simulación de Monte Carlo, con 10 000 ensayos, se obtiene la probabilidad de falla de la conexión, calculando:
Donde el número de fallas es el número de veces en que C > R en los ensayos realizados.
El costo esperado en el ciclo de vida E[CT] del edificio se expresa usualmente (Kishi et al., 2004) como:
Donde C i es el costo inicial del edificio y E[Cd] el costo de daño/falla del edificio, expresado en el ciclo de vida y en términos de valor presente, y se suele representar (Guo et al., 2006) como:
Donde:
FVP es el factor de valor presente:
Donde:
r = tasa anual neta de descuento
T = vida útil del edificio
Y Cd es el costo de daño/falla que incluye las pérdidas asociadas a fatalidades, el edificio, los contenidos y los ingresos no obtenidos por la suspensión de actividades económicas en el edificio.
Datos del edificio, cargas y costos
El edificio considerado tiene 11 niveles y su planta no regular, con 8 paneles de 7.2 m X 7.2 m, tiene un cubo hueco de 21.6 m X 21.6 m casi al centro de la planta y una abertura de esquina de 21.6 m X 14.4 m, como se observa en la Figura 2.
Las cargas muertas se determinan con los pesos de los elementos estructurales y no estructurales del edificio. Las secciones transversales de los miembros estructurales se muestran en la Tabla 1.
Tabla 1: Localización y tipo de perfil de miembros estructurales
| Localización | Miembro | Niveles | Perfil | Dimensiones | Unidades |
|---|---|---|---|---|---|
| Columnas | 1 a 3 | Cajón cuadrado | 25x25x2 | ||
| 4 a 7 | 20x20x1 1/2 | ||||
| 8 a 11 | 18 x 18 1 1/2 | ||||
| Perímetro del edificio | Contravientos | 1 a 3 | 12 x 10 3/4 | in | |
| 4 a 7 | HSS | 10 x 8 x 5/8 | |||
| 8 a 11 | 8 x 8 x 1/2 | ||||
| Vigas primarias | 1 a 3 | 18 x 311 | |||
| 4 a7 | 18 x 258 | ||||
| 8 a 11 | 16 x 100 | ||||
| Interior del edificio | Columnas | 1 a 3 | 27 x 539 | ||
| 4 a 7 | 21 x 201 | ||||
| 8 a 11 | W | 18 x311 | in x lb/ft | ||
| Vigas primarias | 1 a 3 | 14 x 82 | |||
| 4 a 7 | 14 x 53 | ||||
| 8 a 11 | 14 x 38 | ||||
| Vigas secundarias | 1 a 3 | 12 x 58 | |||
| 4 a 7 | 12 x 50 | ||||
| 8 a 11 | 12 x 40 |
Las cargas vivas, obtenidas de normas vigentes en México (GDF, 2004) se muestran en la Tabla 2:
Tabla 2: Cargas vivas para edificios, de acuerdo con normas mexicanas (GDF, 2004)
| Localización | Valor |
|---|---|
| Azotea | 100 kg/m2 |
| Azotea, instantánea | 70 kg/m2 |
| Entrepisos | 250 kg/m2 |
| Entrepisos, instantánea | 180 kg/m2 |
El espectro de sismo recomendado para la zona IIIc de la Ciudad de México, de acuerdo con la zonificación prevista en la misma norma y según la localización del edificio (zona de la Av. Paseo de la Reforma) se expresa, como fracción de “g”, la aceleración de la gravedad, como:
Donde los parámetros c, a0, Ta , Tb y r aparecen en la Tabla 3.
Tabla 3: Parámetros para calcular el espectro de aceleraciones (GDF, 2004)
| Zona | c | a0 | Ta | Tb | r |
|---|---|---|---|---|---|
| I | 0.16 | 0.04 | 0.2 | 1.35 | 1.0 |
| II | 0.32 | 0.08 | 0.2 | 1.35 | 1.33 |
| IIIa | 0.40 | 0.10 | 0.53 | 1.8 | 2.0 |
| IIIb | 0.45 | 0.11 | 0.85 | 3.0 | 2.0 |
| IIIc | 0.40 | 0.10 | 1.25 | 4.2 | 2.0 |
| IIId | 0.30 | 0.10 | 0.85 | 4.2 | 2.0 |
El espectro resultante para la zona IIIc, se observa en la Figura 3, donde la meseta central con aceleración constante tiene como rango de abscisas [Ta, Tb] y a0 es la aceleración ordenada en el origen, en roca.
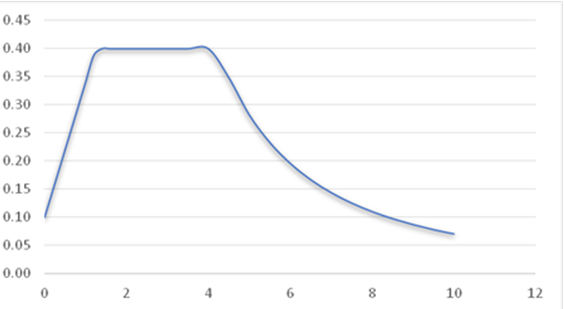
Figura 3: Espectro de aceleraciones, como fracción de“g”, para la zona IIIc de la Ciudad de México (GDF, 2017)
De acuerdo con estudios previos (Goel & Chopra, 1997) el periodo fundamental de la estructura se estima con la Ecuación (18), si la altura h del edificio se encuentra en m:
Con ello, para el edificio en cuestión, el periodo fundamental resulta en 1.31 seg.
En la siguiente sección se presentan las propiedades mecánicas del tipo de acero utilizado y los tipos de conexiones empleados en el presente trabajo.
Materiales y tipos de conexiones consideradas
Para todos los miembros estructurales, se utilizaron las siguientes propiedades mecánicas:
Acero A-36, (Fy = 2530 Kg/cm2), E= 2 050 000 kg/cm2
Fu = 4 080 kg/cm2
Criterio de Von Mises para endurecimiento por deformación
Tornillos de alta resistencia A-325, E= 2 110 000 kg/cm2, Fy = 6,330 kg/cm2, Fu= 8 440 kg/cm2
Las siguientes conexiones se emplearon como alternativas de conexión 1, 2 y 3 como se observa en la Figura 4.
Resultados
Siguiendo el procedimiento antes descrito, se calculan los momentos máximos por nivel, mediante análisis no lineales bajo carga gravitacional y sismo para el espectro medio de la Figura 3. Los momentos máximos M1 y M2, en el plano del marco y transversales a él, son las respuestas asociadas al espectro medio, pero pueden calcularse también para otras aceleraciones obtenidas factorizando el espectro de la Figura 3. Así se obtiene la función de momentos máximos en términos de la aceleración. Como un ejemplo, la Tabla 4 muestra los momentos máximos para el espectro recomendado para la zona donde se encuentra el edificio considerado en el estudio.
Tabla 4: Momentos máximos para el espectro de aceleraciones de la norma
| Nivel | Momentos máximos[Tn-m] | |
|---|---|---|
| M1 | M2 | |
| 1 | 10.43 | 14.34 |
| 2 | 11.24 | 14.88 |
| 3 | 11.56 | 15.67 |
| 4 | 11.98 | 15.97 |
| 5 | 12.12 | 17.23 |
| 6 | 12.02 | 17.54 |
| 7 | 11.88 | 17.66 |
| 8 | 11.65 | 15.87 |
| 9 | 10.44 | 14.22 |
| 10 | 9.32 | 12.18 |
| 11 | 9.21 | 11.09 |
Por otra parte, los estados límite de las conexiones se exploran mediante análisis de elemento finito sometiendo cada conexión a valores crecientes de momentos hasta alcanzar la capacidad en cada tipo de estado límite, como se observan en la Tabla 5.
Tabla 5: Estados límite y capacidades (Kg-m) de los 3 tipos de conexión
| Identificador | Estado límite | Conexión | ||
|---|---|---|---|---|
| CPT-01 | CPT-02 | CPT-03 | ||
| I | Momento plástico de viga (AISC) | 21 110 | ||
| II | Momento plástico de viga (NTC) | 19 000 | ||
| III | Capacidad a flexión placa de extremo | 19 720 | 32 920 | 45 500 |
| IV | Capacidad de flexión patín de columna | 12 250 | 12 250 | - |
| V | Capacidad a flexión alma de columna | 6 717 | 6 717 | 8 410 |
| VI | Fluencia de alma de columna | - | - | 4 480 |
| VII | Desgarramiento de alma de columna | - | - | 8 210 |
| VIII | Flexión de patín de columna | - | - | 5 900 |
De la Tabla 5 se puede identificar el estado límite más desfavorable. Con esta información, se grafican los resultados de los modelos de elemento finito, momentos y rotaciones para generar curvas momento rotación ante carga cíclica para las tres conexiones y para el estado límite más desfavorable, asimismo, se utilizan como valores medios de las capacidades de las conexiones. Las curvas se muestran en la Figura 5.
De acuerdo con las expresiones (3) a (10), se procede al análisis probabilista de las conexiones. La caracterización de las resistencias se sintetiza en la Tabla 6 y las demandas máximas en la Tabla 7.
Tabla 6: Media, coeficiente de variación y desviación estándar de resistencias para las tres conexiones
| Modelo de conexión | Momentos máximos [µR] | Coeficiente de variación [CVR] | Desviación estándar [σR] |
|---|---|---|---|
| Tn - m | Tn - m | ||
| CPT-01 | 13.37 | 0.1 | 1.337 |
| CPT-02 | 17.58 | 0.1 | 1.758 |
| CPT-03 | 18.95 | 0.1 | 1.895 |
Tabla 7: Media, coeficiente de variación y desviación estándar de demandas máximas para las tres conexiones
| Modelo de conexión | Momentos máximos [µC] | Coeficiente de variación [CVC] | Desviación estándar [σC] |
|---|---|---|---|
| Tn - m | Tn - m | ||
| CPT-01 | 12.03 | 0.3 | 3.609 |
| CPT-02 | 13.49 | 0.3 | 4.047 |
| CPT-03 | 15.08 | 0.3 | 4.524 |
Las probabilidades condicionales de falla de las tres conexiones, que se calculan con 10,000 simulaciones de Monte Carlo, resultan: 0.2732, 0.1224 y 0.1766 para las conexiones 1, 2 y 3, respectivamente. Considerando la probabilidad de ocurrencia de la aceleración 0.4 g (la más probable, de acuerdo con un trabajo previo), es de 0.0385. Por tanto, las probabilidades incondicionales de falla para las conexiones 1, 2 y 3 son: 0.1766, 0.0047 y 0.0067, respectivamente.
De acuerdo con lo descrito en la sección de la metodología, se calculan las probabilidades de falla del edificio, considerando alternativamente las tres conexiones. Los costos esperados se calculan en términos de dicha probabilidad de falla.
Finalmente, los costos se calculan con base en costos del acero y mano de obra usuales en México, considerando que el edificio es de oficinas y la renta es de $ 400 pesos por m2 por mes. El costo de las conexiones (suponiendo todas son iguales en el edificio) se observa en la Figura 6. Asimismo, el costo esperado de fatalidades (de un estudio previo) varía de 80 a 180 millones de pesos. El costo esperado en el ciclo de vida se compara para los tres tipos de conexión, Figura 7.
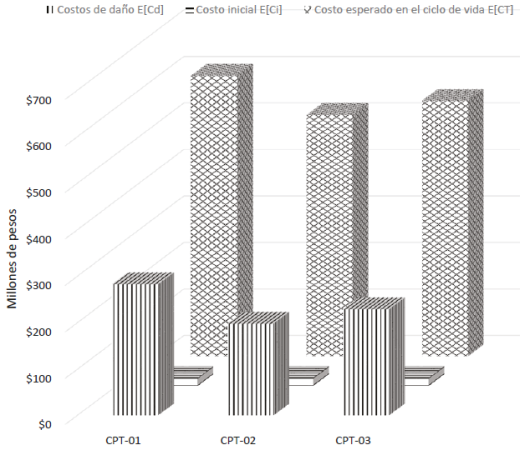
Figura 7: Costo de daño, costo inicial y costo esperado en el ciclo de vida para las tres conexiones
Como se observa en la Figura 6, el costo esperado en el ciclo de vida mínimo es el de la conexión 2. En la Figura 8 se comparan los costos esperados de fatalidades y de pérdida económica, para los tres tipos de conexiones.
Discusión
De los resultados de la sección previa, el tipo óptimo de conexión para el peligro sísmico de la zona IIIc de la Ciudad de México, el tipo estructural, número de niveles y nivel de utilidades del edificio considerado aquí, es el CPT-02. De la comparación entre costos y desempeño de los tres tipos de conexión, se infieren las siguientes observaciones:
Tipo de conexión CPT-01
Aunque esta conexión tiene un costo inicial bajo, debido a los elementos metálicos y proceso constructivo involucrados, tiene un alto número de fatalidades para zonas de alto peligro sísmico y, por tanto, no es la mejor opción por tener una alta probabilidad de falla. Quizás para edificios en sitios de baja sismicidad, con poca ocupación o donde no haya ocupantes, y con bajo nivel de utilidades, esta conexión podría ser la mejor opción.
Tipo de conexión CPT-02
Debido al uso de cartelas, la conexión tipo CPT-02 resulta más resistente que las otras y tiene, en consecuencia, una menor probabilidad de falla y un menor costo esperado de fatalidades. De ahí que tenga el menor costo esperado en el ciclo de vida.
A primera vista, esta conexión con un mayor costo de mano de obra pareciera ser la solución más cara. Sin embargo, debido a su mayor capacidad para disipar energía y mayor resistencia a flexión, la probabilidad de falla es menor. Como consecuencia, los costos esperados de falla y el costo esperado en el ciclo de vida son menores. Este resultado es válido para el tipo de peligro, tipo estructural y nivel de utilidades derivados del servicio ofrecido en el edificio.
Tipo de conexión CPT-03
Este tipo de conexión tiene un costo de mano de obra similar al de la conexión tipo CPT-02 y su desempeño estructural es adecuado debido a que la placa de extremo posiciona la zona de falla potencial, lejos de la junta viga-columna. Esto produce una excursión inelástica con rotaciones inelásticas aceptables. Sin embargo, su probabilidad de falla es 30 % más alta que la de la conexión CPT-02 y, en consecuencia, el costo esperado en el ciclo de vida es un poco mayor que el de la conexión tipo CPT-02. Debido a ello, esta conexión puede ser recomendable para un sistema estructural irregular, pero con sismicidad moderada y con niveles de pérdidas por interrupción del servicio menores que las del tipo CPT-02.
Conclusiones
El uso de cartelas (superior e inferior) en la conexión tipo CPT-02 mejora su comportamiento histerético con ciclos estables de alta capacidad para disipar energía y niveles razonables de rotación inelástica. Lo anterior, produce un balance adecuado entre confiabilidad estructural y un bajo costo esperado en el ciclo de vida. Esta conexión se recomienda para el nivel de sismicidad tipo estructural y nivel de utilidades del edificio considerado aquí.
El uso de eslabones, como los de la conexión tipo 3, para poner la zona de falla lejos de la unión entre viga y columna es una estrategia útil para muchos casos y aunque no resultó ser la solución óptima para el caso considerado aquí, puede serlo para condiciones de sismicidad media y utilidades moderadas. Estudios paramétricos adicionales permitirán definir con mayor precisión los rangos de sismicidad y utilidades donde esta conexión se convierte en solución óptima.
Dado que el tipo de conexión CPT-01 es la conexión más sencilla de las tres aquí consideradas, tuvo la mayor probabilidad de falla y, aunque el costo inicial es el menor, tiene los mayores costos esperados en el ciclo de vida. Para zonas de sismicidad baja, o donde la ocupación es baja o no hay ocupantes, este tipo de conexión puede ser la que se recomiende.
Se ha presentado un modelo probabilista que mide el equilibrio y la efectividad económica entre tres alternativas de conexiones de acero, que incluye las incertidumbres en la intensidad sísmica y las resistencias, así como las consecuencias económicas de la interrupción del servicio del edificio y las fatalidades potenciales, para la sismicidad típica de la zona blanda en la Ciudad de México.
Para otros niveles de peligro sísmico, otros tipos de estructuras, otros niveles de pérdidas y otros tipos de conexiones, deben hacerse los ajustes correspondientes antes de poder generalizar los resultados.
La variable del tiempo de ejecución es una que no fue considerada y, en determinados proyectos, puede ser determinante.
Se necesita explorar otros mecanismos de falla, así como la consideración de estados límite de servicio.
Deben realizarse estudios para otras zonas sísmicas, otras construcciones, otros niveles de pérdidas y otros tipos de conexiones para actualizar la normatividad y la práctica de ingeniería de estructuras de acero en México.











 nueva página del texto (beta)
nueva página del texto (beta)








